| NO.1431 | 2003.12.1. | 松井 満 | 折り曲げた板の回転体(3) |


| NO.1432 | 2003.12.12. | 水の流れ | 整数三角形 |
今回は、「中尾」さんからの出題で、「3辺の長さが整数の三角形」に関するものです。
問題1.:
3辺の長さa,b,cが全て整数である三角形で、底辺aが高さhの5倍に等しいものをいくつか求めなさい。
(<水の流れ:1個でも構いません>)
問題2:
3辺の長さa,b,cが全て整数である三角形で、
底辺aが高さhの6倍に等しいものをいくつか求めなさい。
(<水の流れ:1個でも構いません>)
問題3:
3辺の長さa,b,cが全て整数である三角形で、
底辺aが高さhの2倍に等しいものは存在しないことを証明しなさい。
ただし、相似な(または合同な)三角形は同一と見なします。

| NO.1433 | 2003.12.12. | 水の流れ | 小町算2004(1) |
皆さん, 小町算(こまちざん)を存知ですか。
小町算・・・1,2,3,4,・・・、9の間に+、−、×、÷等の計算記号を入れて、
その計算をした答えが100とかあるいは99などのある特定の数にする計算の遊びです。
来年は西暦2004年なので、ここで問題です。
問題1:
1,2,3,4,・・・、9の間に+、−、×、÷等の計算記号を入れて、その計算をした答えが
2004にしてください。
<例 1−2+345×6+7−8×9=2004>
さらに、w.w.R.ボールさんが1913年に4を4つ使っていろいろな自然数を作ってみようと
提案したのが起源とされています。
例えば、
0=44−44
24=4!−(4−√4−√4)
39=44−(√4÷.4)・・・
使える記号 四則演算(+,−,×,÷,√ ,!,ガウス記号[ ],・・・)
使える数字
4!=4×3×2×1=24
.4=0.4
..4=0.04
...4=0.004
.4(・)=0.444・・・=4/9
そこで、来年は西暦2004年なので、ここで問題です。
問題2:4を4つ使って2004を表してください。
<例 (4+4)÷...4+4=2004>

| NO.1434 | 2003.12.14. | 小学名探偵 | 条件を満たす多項式の個数 |
(問題) * 一部訂正12/24
F(n)はz個の因数の積で表現される正整数nのz次多項式です。
各因数は正整数で、(n+c)で表現されます(cは整数です)。因数間の差(絶対値)は2以下です。
かつ、n >=(z+1)/2 の条件下にあります。
nz<F(n)<(n+1)z
を満たすnのz次多項式F(n)の数A(z)の数列はどのようになりますか。
(例えば、z=2(2次)のとき、n*(n+1)は上の条件を満たす多項式F(n)の1つです。A(1)は明らかに0です。)

| NO.1435 | 2003.12.20. | teki | 小町算2004(2) |
問題1:
各数字をばらばらで使うという条件を加えても、( )を使えばできますね。
例 1+2+3+(4+5×6×7+8)×9=2004
問題2:
こんなもんでいいんでしょうか?
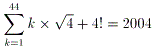

| NO.1436 | 2003.12.21. | H.Nakao | 2004に関する問題 |
1. 3辺の長さが全て有理数である直角三角形で、その面積が2004であるものをいくつか(1個以上)求めなさい。
2. 1辺の長さが共に有理数である2つの立方体で、
その体積の和が2004であるものをいくつか(1個以上)求めなさい。

| NO.1437 | 2003.12.24. | 小学名探偵 | 多項式の不等式条件の成否を問う問題 |
(問題)
正整数n、kについて、
(1) = k-1のとき(かつ、2k+1 ≧ 5)、
n2k+1<(n+2)k+1*nk<(n+1)2k+1
が成り立ち、
n2k+1<(n+1)k+1*(n-1)k
が成り立たない、という命題は真理ですか。
(2)n ≦ k-1のとき(かつ、2k+1 ≧ 5)、
n2k+1<(n+2)k+1*nk<(n+1)2k+1
が成り立ち、
n2k+1<(n+1)k+1*(n-1)k
が成り立たない、という命題は真理ですか。
(3)n = k+1のとき(かつ、2k+1 ≧ 3)、
n2k+1<(n+1)k+1*(n-1)k<(n+1)2k+1
が成り立ち、
(n+2)k+1*nk<(n+1)2k+1
が成り立たない、という命題は真理ですか。
(4)n ≧ k+1のとき(かつ、2k+1 ≧ 3)、
n2k+1<(n+1)k+1*(n-1)k<(n+1)2k+1
が成り立ち、
(n+2)k+1*nk<(n+1)2k+1
が成り立たない、という命題は真理ですか。
(5)n = kのとき(かつ、2k+1 ≧ 3)、
n2k+1<(n+1)k+1*(n-1)k<(n+1)2k+1
が成り立たず、
n2k+1<(n+2)k+1*nk<(n+1)2k+1
が成り立たない、という命題は真理ですか。

 E-mail
E-mail
 戻る
戻る