| NO.1438 | 2004.1.1. | Junko | 
|
新年あけましておめでとうございます。
昨年は、今までになく仕事が忙しく、皆様にはご迷惑をおかけしました。
今年も忙しいのかな?
忙しくとも自分らしさを大切にしていきたいと思っています。
今年もどうぞよろしくお願いいたします。
(画像提供 LITTLE HOUSE)

| NO.1439 | 2004.1.1. | Junko | algo |
最近小学生の間で流行っているゲームがあると聞いて、私も買ってみました。
「algo」と言って書店などで売っています。算数オリンピック委員会が開発、
箱には「頭のよくなるゲーム」とあります。ルールはむずかしくありません。相手のカードの数字を当てるゲームです。
でもこれが結構なかなかおもしろいです。頭がよくなるかどうかは別として、
お正月のテーブルゲームとしておすすめです。
詳しくは、こちら → algo

| NO.1440 | 2004.1.1. | 小学名探偵 | 差2以下の多因数分解の一意性 |
NO.1437「多項式の不等式条件の成否を問う問題」
の関連問題として、下記の問題を投稿します。
(問題)
F(z)=(n+2)a*(n+1)b*nc
(nは正整数、 a, b, cは非負の整数、かつ a+b+c > 0)
に関する一意性について考えてみましょう。
(1)(n+2)a1*(n+1)b1*nc1
= (n+2)a2*(n+1)b2*nc2
(a1, b1, c1, a2, b2, c2 は非負の整数、かつ a1+b1+c1=a2+b2+c2 >0)
が成立するのはa1=a2, b1=b2, c1=c2のときに限られますか。
(2)(n+3)a1*(n+2)b1*(n+1)c1
= (n+2)b2*(n+1)c2*nd2
(a1, b1, c1, b2, c2, d2 は非負の整数、かつ a1+b1+c1=b2+c2+d2 >0)
が成立するのはa1=0, b1=b2, c1=c2, d2=0のときに限られますか。
(3)(m+2)a1*(m+1)b1*mc1
= (n+2)a2*(n+1)b2*nc2
(m, nは正整数、a1, b1, c1, a2, b2, c2 は非負の整数、かつ a1+b1+c1=a2+b2+c2 >0)
が成立するのはm=n, a1=a2, b1=b2, c1=c2のときに限られますか。

| NO.1441 | 2004.1.1. | yokodon | サイクロイドの性質 |
~模試シリーズ号外・サイクロイドの性質~
サイクロイド曲線の一部:
x = θ- sinθ 、y = 1 - cosθ 、0 ≦θ≦ π
をC、点P (a, 1) を中心として点H (a, 0) で x 軸に接する円をAとする。但し
、a は実数とする。
(1)円Aが曲線Cと異なる2点で交わるための a の値の範囲を求めよ。
(2)a > 0 とする。円Aが曲線Cと2点で交わるとき、その x 座標の小さい方の
点をQとする。Qの座標と、角度∠QPHの大きさを求めよ。
(3)曲線C、円A及び x 軸で囲まれた領域の面積がQの x 座標に等しいことを証
明せよ。
おまけ:時間のある方に
(4)(3)の結果を、サイクロイドの性質から説明してみて下さい。

| NO.1442 | 2004.1.1. | 水の流れ | 大ピラミッド |
エジプトのピラミッドは世界の7不思議のひとつとして数えられています。
多くの人の興味と関心の対象です。この古代ピラミッドに隠れている不思議を紹介します。
モール師(フランスのカトリック布教者、天文学者)によれば、エジプトの神官たちは、
ヘロドトス(BC484からBC430)に向かって、
大ピラミッドの底辺と高さの関係は、高さを1辺とする正方形の面積が斜面の三角形の
1つの面積に等しくなるように作られていると説明したそうです。この説明を式で表現してみます。
下の図のように、ピラミッドの高さをh、底面の正方形の1辺を2a、斜面の三角形の高さをxとする。
ここで、問題です。
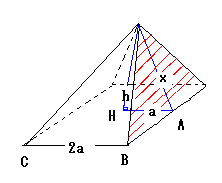
質問1.説明されている関係をx、aで表せ。
質問2.x/a=Xとするとき、Xの値を求めよ。また、このXの値を何と呼ばれているか。
質問3.底面の面積をS,側面の全面積をS1,大ピラミッドの全表面積をS2としたとき、
S,S1,S2をaとxで表せ。また、S:S1=S1:S2を示せ。
質問4.実際に計測しますが、ここでの長さの単位はエジプト王室肘尺で1肘尺は0.524mを使います。
底辺の長さは2a=440肘尺、高さはh=280肘尺となります。このピラミッドのとき、
(1)x/a=Xの値を計算してください。
(2)底辺の長さの合計8aと高さの2倍2hの比(8a/2h)を求めよ。また、 この比の値を何と呼ばれているか。
<参考文献1.「数とその歴史」上垣 渉・何森 仁 共著 三省堂
2.「数学の不思議」柳谷 晃 著 かんき出版>

| NO.1443 | 2004.1.11. | 三角定規 | 等辺正多面体 |
辺の長さがすべて等しい5つの正多面体を作ってみました。
正多面体については,オイラーの定理を始めとして,いろいろなことを知っているつもりでおりました。
小学生の算数の教科書にも載っているくらいですから…。
ですが,等辺のものを作るのは初めてで,作ってみて新しい発見がいくつもありました。
まず気がついたのは,その大きさの違いです。写真をご覧ください。
最大の正十二面体の体積は,最小の正四面体のそれの約65倍もあります。

さらに,その大きさの順序関係です。
別に根拠があったわけではありませんが,
面数が多くなるほど大きくなるものと思い込んでいました。
正多面体の美しい図や写真が載っているサイトはたくさんありますが,
それらは断面がほぼ同じ大きさになるように作られているものが多いようです。
意図的にこうしているのでしょうか。すると,面数が多く球に近く見えるものほど大きく見えてしまうものです。
これが上の思い込みの原因か…とも思います。
体積は,正四,正八,正六,正二十,正十二面体の順に大きくなり,
これは,頂点の数の順でもあります。もちろん,比例しているわけではありませんが…。
いろいろ計算してみました。一辺が1の正多面体の諸量です。
| 正四面体 | 正六面体 | 正八面体 | 正12面体 | 正20面体 | |
|---|---|---|---|---|---|
| 外接球の半径R | 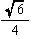 =0.61 | 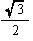 =0.87 | 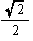 =0.71 | 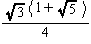 =1.40 | 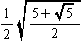 =0.95 |
| 中接球の半径ρ(注) | 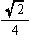 =0.35 | 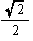 =0.71 | 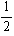 =0.50 | 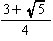 =1.31 | 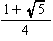 =0.81 |
| 内接球の半径r | 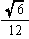 =0.20 | 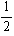 =0.50 | 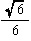 =0.41 | 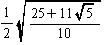 =1.11 | 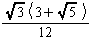 =0.76 |
| 体 積 v | 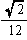 =0.12 | 1 | 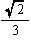 =0.47 | 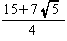 =7.66 | 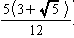 =2.18 |
| 外接球の体積V | 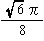 =0.96 | 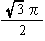 =2.72 | 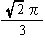 =1.48 | 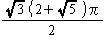 =11.53 | 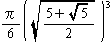 =3.60 |
充填率 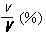
| 12.3 | 36.8 | 31.8 | 66.5 | 60.5 |
| 2面のなす角 | 70.5゚ | 90゚ | 109.5゚ | 116.6゚ | 138.2゚ |
(注) 中接球:辺に接する球,半径は中心から辺の中点までの距離
上に,「面数が多いほど球に近い」と書きました。
私は,このことの量的表現は「充填率」だと思っておりました。
しかし,これだと正十二面体の方が大きくなります。
やはり,「球への近さ」は「2面のなす角」でしょうか。

| NO.1444 | 2004.1.11. | 水の流れ | フィボナッチ数 |
1202年、イタリアに住んでいたフィボナッチは当時の代数学と整数論の知識を総合した内容の
「算盤の書」という名の本をラテン語で出版しました。
これは10進法を用いて学習するヨーローパで最初の本の1冊となりました。
フィボナッチは当時の風習であった数学競技会(難しい問題を最高・最速で解く公開競技)に参加しました。
フィボナッチの問題を解く手法はみんなを驚かせました。
フィボナッチの名声は、数学グループを同行してローマ帝国のピザを訪れた
フリードリッチⅡ世皇帝にまでとどろきフィボナッチとの公開試合が催されました。
試合に出題された問題の一つは次に示す問題です。
「平方に5を加えても、平方から5を引いても完全平方となる数を見つけよ」ただし、このような数は分数で、整数ではありません。
また、フィボナッチは1つ数を見つけましたが、他にもありそうです。
<問題出典:「数学センス」コルディムスキー 著 鈴木敏則 訳 (丸善株式会社)>

| NO.1445 | 2004.1.11. | 水の流れ | ガウス・グリーンの定理 |
媒介変数tで表された関数で、t=αからt=βまで動くとき、
その線分OPの通過してできる領域の面積を求めるのに役立ちます。

ここで、次の問題に従来の方法とガウス・グリーンの定理の両方で解いてみてください。
「媒介変数tを用いて、x=cost+tsint , y=sint-tcost で定まる点P(x,y)について、 tが 0≦t≦π で動くとき線分OPが通過してできる領域の面積Sを求めよ。」
<参考文献>「大学への数学H15年9月・11月号」(東京出版)

 E-mail
E-mail
 戻る
戻る