| NO.1416 | 2003.11.1. | yokodon | 僛乕僞娭悢偺抣兡(2) |
嬼慠丄偙傫側偺傪尒偮偗傑偟偨丅
庒姳丄僆儕僕僫儖偲堘偆晹暘傕偁傝傑偡偑丄
杮幙揑側偲偙傠傪懝側傢側偄斖埻偱屼徯夘偟偨偄偲巚偄傑偡丅
乵栤戣乶
(1)n 傪旕晧惍悢偲偡傞丅埲壓傪帵偣丅
丂丂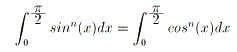
(2)
丂丂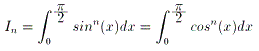 丂丂偲偍偔丅師幃傪帵偣丅
丂丂偲偍偔丅師幃傪帵偣丅
丂丂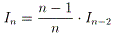
(3)In 傪 n 偺幃偱昞偣丅
(4)
丂丂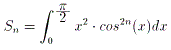 丂丂偲偍偔丅師幃傪帵偣丅
丂丂偲偍偔丅師幃傪帵偣丅
丂丂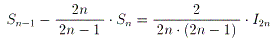
(5)N 傪帺慠悢偲偡傞丅師幃傪帵偣丅
丂丂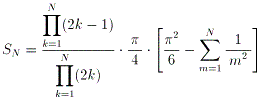
(6)師幃傪帵偣丅
丂丂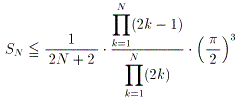
扐偟丄昁梫側傜 0 亙 x 亙 兾/2 偱丄x 亙 兾/2 丒sin(x) 偱偁傞偙偲傪梡偄偰傛偄丅
(7)埲忋傪梡偄偰丄
丂丂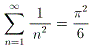
丒丒丒偱偁傞偙偲傪帵偣丅
偙傟偱丄崅峑傑偱偺悢妛傪梡偄偰丄兡(2) 偺抣偑寁嶼偱偒傑偡偹丅
椶帡偺岺晇偱丄懠偺抣傕寁嶼偱偒傞偺偱偟傚偆偐丠

| NO.1417 | 2003.11.3. | 徏堜丂枮 | 娫愙徹柧(2) |
媣偟傇傝偵夝摎傪憲傜偣偰偄偨偩偒傑偡丅 婔壗妛揑側偡偭偒傝偟偨曽朄偱偼側偄偺偱偡偑丒丒丒

偟偨偑偭偰嶰妏宍ABC偼擇摍曈嶰妏宍偲側傝丄AB=AC偑惉棫偡傞丅

| NO.1418 | 2003.11.3. | sakamoto | 僶儕僄乕僔儑儞偺悢 |
巹偼朸戝嶃偺婇嬈偵偰彜昳奐敪傪扴摉偟偰偄傑偡丅
崱丄彜昳偺僉儍僢僠僼儗亅僘偵傛偔巊梡偝傟偰偄傞
乭乑乑捠傝偺僶儕僄乕僔儑儞乭偺嶼弌偺巇曽偑傢偐傜側偔偰
崲偭偰偄傑偡丅
奐敪拞偺俙彜昳偵偼俋屄偺寠偑偁傝傑偡丄
侾侾庬椶偺崅偝偺朹傪怓乆側慻崌偣偱
擖傟偨帪偵丄俙偼壗僷僞乕儞乮僶儕僄乕僔儑儞乯
弌棃傞偺偐丠乮摨偠崅偝偺朹傪廳暋偟偰巊梡偟偰傕偄偄偱偡丅乯
偲偄偆偺偑幙栤偱偡丅

| NO.1419 | 2003.11.3. | Junko | 僶儕僄乕僔儑儞偺悢(2) |
俋屄偺寠偵朹傪偨偰偰偄偔丄廳暋OK偲偄偆偙偲側傜偽丄
119亖2,357,947,691丂偲偄偆偙偲偵側傝傑偡偱偟傚偆偐丠
偮傑傝丄侾斣傔偺寠偵偳偺朹傪擖傟傞丠丂仺侾侾偲偍傝丅
俀斣傔偺寠偵偳偺朹傪擖傟傞丠丂仺侾侾偲偍傝丅
丒丒丒埲壓俋斣傑偺寠傑偱懕偒傑偡丅乮廳暋弴楍乯

| NO.1420 | 2003.11.3. | yokodon | 愜傝嬋偘偨斅偺夞揮懱 |
乣柾帋僔儕乕僘 17乣
俙俛亖俙俠亖併2 丄佢俛俙俠亖兾/2 偺捈妏嶰妏宍俙俛俠偑偁傞丅俀曈俙俛丆俙俠
乮扐偟丄抂揰傪娷傓乯偺忋偵丄偦傟偧傟揰俹丆俻傪 俙俹亖俙俻 傪枮偨偡傛偆偵庢傞丅
偙偺嶰妏宍俙俛俠傪丄慄暘俹俻傪愜傝栚偵偟偰丄嶰妏宍俙俹俻偲巐曈宍俛俠俻俹偲
偺側偡妏偑 兾/2 偵側傞傛偆偵愜傝嬋偘偨棫懱傪俿偲偡傞丅
棫懱俿傪曈俛俠偺傑傢傝偵侾夞揮偝偣傞偲偒丄俿偺廃媦傃撪晹偺揰偑捠夁偡傞椞堟
偺懱愊傪倁偲偡傞丅俹丆俻偑忋婰偺忦審偱摦偔偲偒偺倁偺嵟彫抣傪媮傔傛丅
P.S. 嫽枴偺偁傞曽偼丄俙俹亖俙俻 偺忦審傪奜偟偰峫偊偰傒偰壓偝偄丅

| NO.1421 | 2003.11.4. | Junko | 僛乕僞娭悢偺抣兡(2) (2) |
搑拞傑偱偱偡偑丒丒丒丅
(1)
丂丂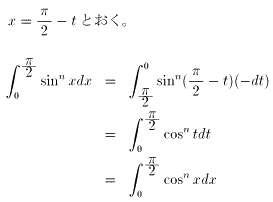
(2)丂晹暘愊暘傪巊偄傑偡丅
丂丂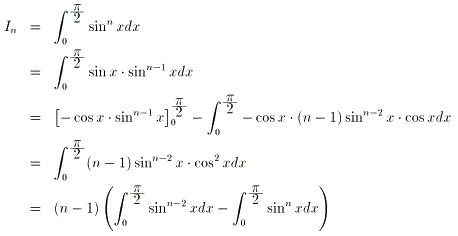
廬偭偰丄In=(n-1)In-2-(n-1)In傛傝丄
丂丂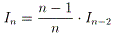
(3)値偑嬼悢偺偲偒
丂丂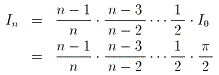
丂値偑婏悢偺偲偒
丂丂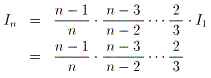
(4)丂晹暘愊暘傪巊偄傑偡丅
丂丂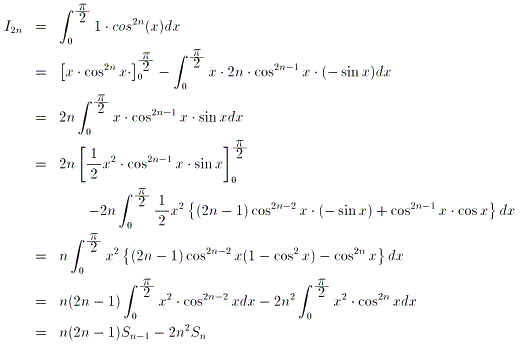
廬偭偰丄
丂丂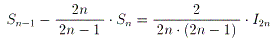

| NO.1422 | 2003.11.4. | 悈偺棳傟 | 柍尷崀壓朄 |
僊儕僔儍帪戙偐傜抦傜傟偰偄偨柍尷崀壓朄偼丄峀偄斖埻偺栤戣傪夝偔嫮椡側曽朄偲偄偊傞丅
曽掱幃偑夝傪帩偨側偄偲偐嶌恾偑晄壜擻偩偲偐偄偭偨斲掕揑側寢榑傪摫偔偺偵摿偵桳岠偱偁傞丅
揟宆揑側棙梡朄傪嫇偘偰傒傑偡丅
梌偊傜傟偨栤戣偑夝俽傪傕偮偲偡傞丅
偁傜偐偠傔栤戣偺惈幙偐傜偳傫側夝偺楍傕桳尷偱僗僩僢僾偡傞偙偲傪偄偭偰偍偄偰丄
俽偐傜弌敪偟偰柍尷偵懕偔夝偺楍傪峔惉偡傞丅
偙偆偟偰丄傕偲偺栤戣偵偼夝偑側偄偙偲傪寢榑偡傞丅
偱偼丄栤戣偱偡丅
曽掱幃丂倶俀乗俀倷俀亖侽偼帺慠悢夝傪傕偨側偄偙偲傪帵偟側偝偄丅
亙夝摎亜
帺慠悢夝乮倶丄倷乯亖乮倎侾丆倐侾乯偑懚嵼偟偨偲偡傞丅
偡側傢偪丄a侾俀乗俀倐侾俀亖侽丂乧嘆丂偲偡傞丅
偙偺偲偒丄a侾偼嬼悢丄偡側傢偪丄a侾亖俀倎俀丂
偲側傞帺慠悢倎俀偑懚嵼偡傞丅偲偡傞偲丄
丂丂丂丂乮俀倎俀乯俀乗俀倐侾俀亖侽丂丂側偺偱丄
俀倎俀俀乗倐侾俀亖侽丂乧嘇丂
偙傟偐傜丄倐侾偼嬼悢丄偡側傢偪丄倐侾亖俀倐俀丂
偲側傞帺慠悢倐俀偑懚嵼偟丄
丂丂丂丂俀倎俀俀乗乮俀倐俀乯俀亖侽丂丂側偺偱丄
倎俀俀乗俀倐俀俀亖侽丂乧嘊
偙傟偼丄乮倎俀丆倐俀乯偑傕偲偺曽掱幃偺帺慠悢夝偱偁傞偙偲傪堄枴偟偰偄傞丅
偲偙傠偑丄嘆丄嘇丄嘊偐傜丂倎侾亜倐侾丄丂倐侾亜倎俀丂丄
倎俀亜倐俀
偮傑傝丄倎侾亜倐侾亜倎俀亜倐俀
偝傜偵丄嘊丂偐傜丄倎俀亖俀倎俁丂偲側傞帺慠悢倎俁偑懚嵼偟偰丄丒丒丒
偙偺傛偆偵丄摨條側棟榑傪孞傝曉偡偲丄尭彮偟懕偗傞帺慠悢偺柍尷楍
丂丂丂丂倎侾亜倐侾亜倎俀亜倐俀
亜倎俁亜倐俁亜倎係亜倐係亜丒丒丒
偑摼傜傟傞丅偲偙傠偑丄帺慠悢倎侾傛傝傕彫偝偄帺慠悢偼桳尷屄偟偐側偄偺偱丄偙傟偼柕弬偟偰偄傞丅
偟偨偑偭偰丄嵟弶偺曽掱幃偺帺慠悢夝偼側偄丅
亙拲堄亜
偙偺夝摎偼丄併俀偑柍棟悢偱偁傞偙偲偺徹柧偵傕側偭偰偄傞丅
丂亙嶲峫暥專亜
乽傔偞偣丄悢妛僆儕儞僺僢僋両丂挊幰丂俰丄僐僼儅儞丄栿丂嶳壓弮堦乿乮尰戙悢妛幮乯

| NO.1423 | 2003.11.5. | 杮懡嬘椇 | Bezier嬋慄偺栤戣(9) |
Bezier嬋慄偺栤戣(9) 亂姰寢曇亃
梌偊傜傟偨Bezier嬋慄偺僆僼僙僢僩嬋慄傪丄惛搙椙偔偐偮峔惉揑偵嬤帡偱媮傔傞
栤戣偱偡偑丄嬤帡僆僼僙僢僩嬋慄帺恎傪Bezier宆幃偱昞尰偡傞傾儖僑儕僘儉傪夝
愢偟偨榑暥偑尒偮偐傝傑偟偨偺偱丄偛曬崘偟傑偡丅
丂Computer Aided Geometric Design Vol.5, No.1, June 1988, pp.33-40
丂"Spline Approximation of Offset Curves", J. Hoschek
僐儘僉僂儉幒NO.1200偺婰崋傪巊偭偰傾儖僑儕僘儉偺慹嬝傪彂偄偰傒傞偲丗
亂侾亃丂P1丄P4乮抂揰傕偟偔偼傾儞僇乕億僀儞僩偲屇偽傟傞乯偺僆僼僙僢僩揰偼
偦偺揰偱偺朄慄曽岦偵L偩偗堏摦偟偨揰偱偁傝帺柧丅
亂俀亃丂P1丄P4埲奜偱嬋慄 C忋偺偄偔偮偐乮屄悢偼榑暥拞偱柧帵乯偺揰傪慖傃丄
忋偲摨條偵僆僼僙僢僩揰傪媮傔傞乮摉慠尩枾偵媮傑傞乯丅
亂俁亃丂儀僋僩儖P1仺P2丄儀僋僩儖P3仺P4丂偺俀偮偺儀僋僩儖偼丄偦傟偧傟偑暲
峴偱挿偝偺堎側傞儀僋僩儖偵堏偝傟傞乮儀僕僃嬋慄偺掕媊傛傝柧傜偐乯丅偙傟傜
偺俀偮偺儀僋僩儖偺斾椺掕悢傪偦傟偧傟兩1丆兩2偲偡傞丅
亂係亃丂嵟彫俀忔朄傪巊偭偰兩1丆兩2偺嵟揔夝傪尒偮偗傞乮嵟揔壔偡傞娭悢傗惂
栺忦審偼榑暥偵柧婰偝傟偰偄傞乯丅
亂俆亃丂嵟彫俀忔朄偱偼亂俀亃偺揰傪慖傫偩偲偒偺 t偺慻傒崌傢偣偵埶懚偡傞偺
偱丄偙傟傪慖傃捈偡偐偳偆偐峫椂偡傞乮仸侾乯丅偦偺屻偱巆嵎乮掕媊偼榑暥拞偵
柧帵乯傪寁嶼丅
亂俇亃丂梊傔掕傔偨岆嵎斖埻偵巆嵎偑擖傟偽姰椆丅梊傔掕傔偨斀暅尷搙夞悢偵払
偟偰偄側偗傟偽亂係亃偵栠傞丄偦偆偱側偄乮斀暅夞悢傪挻偊偰偄傞乯応崌偼丄梌
偊傜傟偨Bezier嬋慄傪擇暘妱乮仸俀乯偟偰丄暘妱偟偨偦傟偧傟偺嬋慄偱亂俀亃偐
傜偼偠傔傞乮偮傑傝丄嵞婣揑偵寁嶼偡傞乯丅
僒僽儖乕僥傿儞偲偟偰巊傢傟偰偄傞仸侾偼丄J. Hoschek帺恎偺懠偺榑暥偱乮忋婰
榑暥偺pp.40 References 偵宖嵹乯丄仸俀偼丄彂愋乽CAGD 偺偨傔偺嬋慄丒嬋柺棟
榑乿嫟棫弌斉姅幃夛幮姧丄傕偟偔偼丄巹偺彂偄偨
僒儞僾儖僐乕僪乮椉幰摨撪梕乯
偱尒傞偙偲偑偱偒傑偡丅傑偨丄旕慄宍娭悢偺嵟彫俀忔朄偵偮偄偰偼偄傠傫側嫵壢
彂偵嵹偭偰偄傑偡偹丅
Adobe Illustrator 偑偙偺榑暥偺曽朄偱Bezier嬋慄偺僆僼僙僢僩傪寁嶼偟偰偄傞
偐偳偆偐偼傢偐傝傑偣傫偑丄僆僼僙僢僩屻偵傾儞僇乕億僀儞僩偺屄悢偑僆儕僕僫儖偺嬋慄偵斾傋
憹壛偡傞尰徾偑偁傞偁偨傝丄偄偐偵傕忋婰亂俇亃偺嵞婣寁嶼
偱傕偟偰偄偦偆側姶偠偱偡丅

| NO.1424 | 2003.11.7. | Junko | 愜傝嬋偘偨斅偺夞揮懱(2) |
壓偺恾偺傛偆偵丄俛俠傪夞揮幉(x)偲偟丄俛俠偺拞揰傪俷偲偟傑偡丅
俙俹亖俙俻亖倲併俀偺偲偙傠偱愜傝嬋偘偨偲偟傑偡丅
棫懱俿傪俛俠傪幉偲偟偰夞揮偝偣偨偲偒偺懱愊傪倁(倲)偲偍偒傑偡丅
夞揮懱偺懱愊傪媮傔傞偵偼丄傑偢偦偺抐柺(墌)偺敿宎倢(倶)傪媮傔傞昁梫偑偁傝傑偡丅
敿宎倢(倶)偺媮傔曽偼丄嘆侽亙倶亝倲偺応崌偲丄嘇倲亝倶亙侾偺応崌偱堎側傝傑偡丅
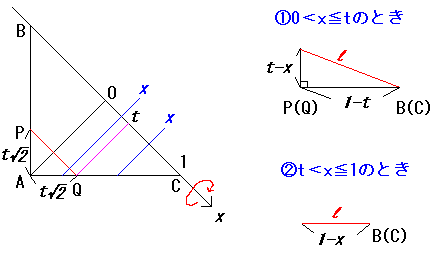
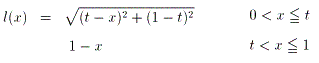
廬偭偰丄夞揮懱偺懱愊傪媮傔傞嵺偵偼丄愊暘嬫娫傪暘偗偰峫偊傞昁梫偑偁傝傑偡丅
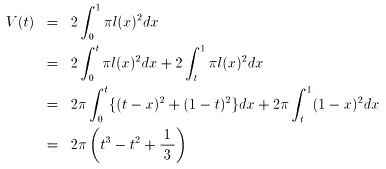
師偵丄媮傑偭偨V(倲)偺嵟彫抣傪媮傔傑偡丅
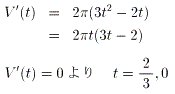
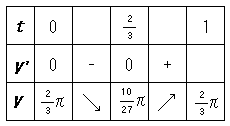
憹尭昞偵傛傝丄嵟彫抣(10/27)兾丂丂(倶亖2/3偺偲偒)

 E-mail
E-mail
 栠傞
栠傞