Weekend Mathematics/コロキウム室/NO.167
| NO.1394 | 2003.5.1. | yokodon | 関数方程式と極限 |
〜模試シリーズ16〜
(1)整式 f(x) が、次の関係式を満たしているものとする。
f(x + 1) = f(x) + xn (n:ある自然数)
このとき、次の極限値を求めよ。
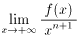
(2)多項式とは限らない連続関数 g(x) が
g(x + 1) = g(x) + xn
を満たしているとき、次の極限値は、問(1)の結果に一致することを証明せよ。
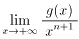
但し、必要なら、閉区間上で連続な関数は必ず最大値と最小値を持つことを用いて良い。
(3):おまけ
問(1)の条件式;f(x + 1) = f(x) + xn ・・・をみたす整式が存在することを証明せよ。

| NO.1395 | 2003.5.8. | みかんさん | 円順列(1) |
質問ですが、もしお時間があれば、教えて下さい。
例えば、1、2、3,4の円順列の総数はというときに、何故、4で割るのか分かりませ
ん。「割る」ということの概念がはっきりしていないせいかもしれませんが、それぞれに
回転すれば同じモノが4つあるから、4で割るということが理解できないのです
ダブっているものを引けばいいのだろうと思うのです。割る、のは何故か。

| NO.1396 | 2003.5.8. | Junko | 円順列(2) |
円順列については、こちらで説明をしています。
確かに混乱するところですよね。
普通の順列で、たとえば「1,2,3,4」とすると、
これを円にした時に、同じものが4つあります。
「1,2,3,4」「2,3,4,1」「3,4,1,2」「4,1,2,3」
ですよね?
普通の順列で「1,2,4,3」とした場合も同じように4つありますよね?
つまり、普通の順列で1つ決めると、円順列では必ず4つづつ同じ
ものが存在してしまうのです。だから4で割るわけです。

| NO.1397 | 2003.5.11. | 水の流れ | 複雑な不定積分 |


| NO.1398 | 2003.5.28. | 水の流れ | ピラミッド問題2 |
太郎さんは、また、「中尾」さんから、次のような類題をもらいました。皆さん!考えてください。
<中尾さんのコメント>前回のLucasのピラミッド問題に関連して、もうひとつの類題を解いてみました。
"ピラミッド型に積んだ球の個数が三角数になる場合を求めよ。"Lucasのピラミッド問題は解が2個でしたが、こちらの問題は解が4個です。
[問題]
同じ大きさの球をピラミッド形に(月見だんごのように、最上部に1個、
次の段に4個、3段目に9個というように)積み上げたものを、平面上に並べ
直すと正三角形に(1列目に1個、2列目に2個、3列目に3個というように)なった。
球は全部で何個あるか?

 E-mail
E-mail
 戻る
戻る