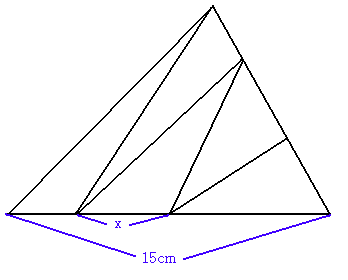
恾偺傛偆偵丄嶰妏宍傪俆偮偺柺愊偺摍偟偄嶰妏宍偵暘妱偟傑偡丅掙曈偺挿偝傪15cm偲偡傞偲丄倶偺挿偝偼壗cm偱偟傚偆偐丅
Weekend Mathematics乛栤戣乛栤戣74
俈係丏柺愊偺摍偟偄嶰妏宍

恾偺傛偆偵丄嶰妏宍傪俆偮偺柺愊偺摍偟偄嶰妏宍偵暘妱偟傑偡丅掙曈偺挿偝傪15cm偲偡傞偲丄倶偺挿偝偼壗cm偱偟傚偆偐丅
僷僘儖傛傝柺敀偄拞妛擖帋偺嶼悢
僺乕僞乕丒僼儔儞僋儖
島択幮
幣拞妛峑'88擖帋丒夵戣
乮儁儞僱亅儉丗偽傫偪傖傫乯
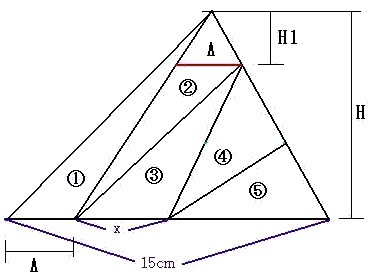
恾偺條偵嶰妏宍偺崅偝傪俫丄嶰妏宍嘆偺掙曈傪俙偲偟傑偡丅
嶰妏宍嘆偺柺愊偼慡懱偺嶰妏宍偺柺愊偺侾乛俆側偺偱
俙偼侾俆亊侾乛俆亖俁們倣偲側傝傑偡丅
枖丄嶰妏宍嘇傕柺愊偑侾乛俆側偺偱嘇偺晹暘偺俙傕俁們倣偲側傝傑偡丅
偙偙偱丄俫侾傪峫偊傞偲
俫侾亖俁乛乮侾俆亅俁乯亊俫亖侾乛係俫偲側傝傑偡丅
屘偵丄嶰妏宍嘊偺崅偝偼嶰妏宍嘆偺崅偝偺俁乛係攞偲側傝傑偡丅
嶰妏宍嘊偺柺愊偑嶰妏宍嘆偲摨偠偵側傞堊偵偼丄
掙曈偑嶰妏宍嘆偺係乛俁攞偵側傜側偗傟偽側傜側偄丅
屘偵丄掙曈倃偼
倃亖俁亊係乛俁亖係們倣偲側傞丅

乮儁儞僱亅儉丗figo乯
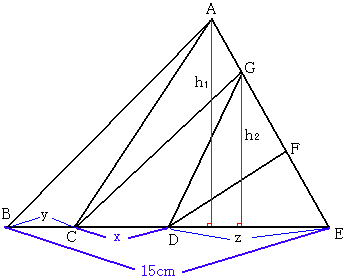
挿偝15偺曈傪掙曈偲偡傞嶰妏宍偺崅偝傪h1,
挿偝x偺曈偺嵍偺曈偺挿偝傪y偲偡傞偲,
挿偝15偺曈傪掙曈偲偡傞嶰妏宍偼柺愊偺摍偟偄嶰妏宍傪
5屄娷傫偱偄傞偺偱
丂丂5*y*h1/2 = 15*h1/2
傛偭偰丂y = 3
傑偨,x傪掙曈偲偡傞嶰妏宍偺崅偝傪h2,
挿偝x偺曈偺塃偺曈偺挿偝傪z偲偡傞偲,
挿偝x+z偺曈傪掙曈偲偟,崅偝h2偺嶰妏宍偼
柺愊偺摍偟偄嶰妏宍傪3屄娷傫偱偄傞偺偱
丂丂3*x*h2/2 = (x+z)*h2/2
傛偭偰 z = 2x
傑偨
丂丂x+y+z = x+3+2x = 3x+3 = 15
偱偁傞偺偱
丂丂x = 4

乮儁儞僱亅儉丗忨偺偍偠偝傫乯
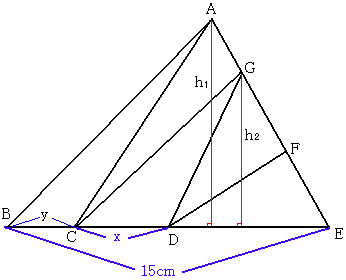
仮ABC偺崅偝傪h1丄掙曈傪y偲偡傞丅
仮GCD偺崅偝傪h2丄掙曈傪x偲偡傞丅
仮ABE偺柺愊偼丄
丂丂S=15亊h1/2=7.5h1丂cm2
俆偮偵暘偗偨侾偮偺嶰妏宍偺柺愊偼丄
丂丂7.5h1/5=1.5h1丂cm2
仮ABC偺柺愊偑丄1.5h1丂cm2偱偁傞偐傜掙曈y傪媮傔傞偲丄
丂丂y丒h1/2=1.5h1丂丂丂y=3丂cm
仮GCE偺柺愊偼丄1.5h1亊3=4.5h1偱偁傞偺偱偙偺嶰妏宍偺崅偝偼師偺條偵媮傔傞偙偲偑偱偒傑偡丅
丂丂(15-3)亊h2/2=4.5h1丂cm2
丂丂h2=(3/4)4.5h1丂cm
仮GCD偺柺愊偼丄x亊(3/4)h1/2=1.5h1丂偲側傝傑偡丅
丂丂x亊(3/4)h1=3h1
掙曈x=4丂cm偱偡丅

乮儁儞僱亅儉丗屵擭偺偆傝傏偆乯
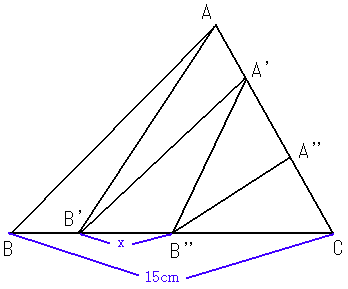
掙曈俛俠偲俙丆俙丩偺崅偝傪偦傟偧傟俫丆倛偲偍偔丅
| 仮俙俛俠 | 亖丂侾乛俀丂亊丂侾俆丂亊丂俫丂亖丂侾俆俫乛俀 |
| 仮俙俛俛丩 | 亖丂侾乛俆丂仮俙俛俠 |
| 亖丂俁俫乛俀 | |
| 亖丂侾乛俀丂亊丂俁丂亊丂俫丂丂丂丂丂丂丂丂亪丂俛俛丩亖丂俁乮噋乯 |
| 仮俙丩俛丩俛丩丩亖丂侾乛俀丂亊丂倶丂亊丂倛丂亖丂俁俫乛俀 | |
| 佁 | 倶倛丂亖丂俁俫丂乧丂嘆 |
| 仮俙丩俛丩丩俠丂亖丂侾乛俀丂亊丂乮侾俀亅倶乯丂亊丂倛丂亖丂俁俫 | |
| 佁 | 乮侾俀亅倶乯倛丂亖丂俇俫丂乧丂嘇 |
倶亗侽丆俫亗侽丆倛亗侽丂偩偐傜丄丂嘇乛嘆丂傛傝丄
| 乮侾俀亅倶乯乛倶丂亖丂俀 | |
| 佁 | 倶丂亖丂係 |
傑偨丄偙傟傪嘆偵戙擖偟偰丄丂丂倛丂亖丂俁俫乛係
廬偭偰丄倶亖係乮噋乯丂乧乮摎乯
偪側傒偵丄俛丩丩俠亖俉乮噋乯

乮儁儞僱亅儉丗aa乯

堦斣嵍偺彫偝偄嶰妏宍偑丄尦偺戝偒側嶰妏宍偺柺愊偺1/5偲偄偆偙偲偼丄偙偺俀偮偺嶰妏宍偺崅偝偼摨偠側偺偱丄掙曈偑尦偺嶰妏宍偺1/5偲偄偆偙偲偱偡丅偡側傢偪丅俁cm丅
傛偭偰丄堦斣塃懁偺彫偝偄嶰妏宍偺掙曈偼丄12-x偵側傝傑偡丅
嵍偐傜3斣栚偺嶰妏宍偲丄塃偐傜1斣栚偲俀斣栚傪堦弿偵偟偨嶰妏宍偼崅偝偑摨偠側偺偱丄偦偺崅偝傪h偲偡傞偲丄柺愊偼丄偦傟偧傟xh/2丄(12-x)h/2偵側傝傑偡丅奺嶰妏宍偼摨偠柺愊側偺偱
丂丂2亊xh/2=(12-x)h/2
丂丂2xh=12h-xh
丂丂3xh=12h
傛偭偰丄x=4(cm)偱偡丅

乮儁儞僱亅儉丗儅僙偑偒乯
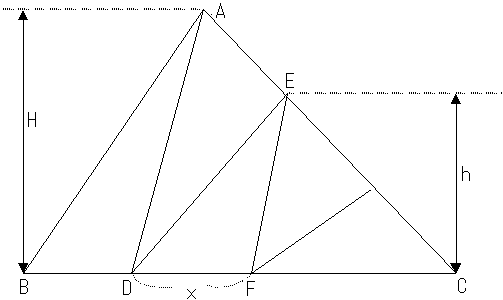
暘妱偝傟偨嶰妏宍偺柺愊偼偦傟偧傟摍偟偄偨傔丄仮ABD偺柺愊偼仮ABC偺柺愊偺俆暘偺侾偲側傞丅傑偨丄仮ABD偺崅偝偲仮ABC偺崅偝偼偄偢傟傕H偲側傝摍偟偄丅偙傟傜偺偙偲偐傜掙曈BD偺挿偝偼丄BC偺俆暘偺侾偲側傞偙偲偑傢偐傞丅
傛偭偰丄俛俢亖侾俆亐俆亖俁丄俢俠亖侾俆亅俁亖侾俀
俛俢偼俁們倣丄俢俠偼侾俀們倣偲側傞偙偲偑媮傔傜傟傞丅
偙偙偱丄仮俤俢俠偵拝栚偟偰傒傞偲丄偙偺嶰妏宍偼暘妱偝傟偨俁屄偺嶰妏宍偱峔惉偝傟偰偄傞偨傔仮俤俢俥偺柺愊偼丄仮俤俢俠偺柺愊偺俁暘偺侾偲側傞丅傑偨丄仮俤俢俥偺崅偝偲仮俤俢俠偺崅偝偼偄偢傟傕倛偲側傝摍偟偄丅偙傟傜偺偙偲偐傜媮傔傞倶丄掙曈D俥偺挿偝偼丄俢C偺俁暘偺侾偲側傞偙偲偑傢偐傞丅
傛偭偰丄俢俥亖侾俀亐俁亖係
倶偼係們倣丒丒丒乮摎偊乯

乮儁儞僱亅儉丗nuno乯丂仺偛楢棈傪偍懸偪偟偰偄傑偡丅
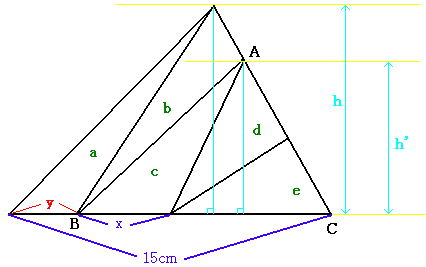
a=(15h/2)亐5=1.5h
1.5h=(1/2)yh丂丂丂仺丂丂丂3h=yh丂丂丂仺丂丂丂y=3
c=d=e丂丂丂c=(1/3)仮ABC
BC=15-3=12
(12h'/2)亐3=c丂丂丂仺丂丂丂c=2h'
c=xh'/2偵戙擖丂丂2h'=xh'/2丂丂丂仺丂丂丂4h'=xh'
x=4

乮儁儞僱亅儉丗僒僟偪傖傫乯
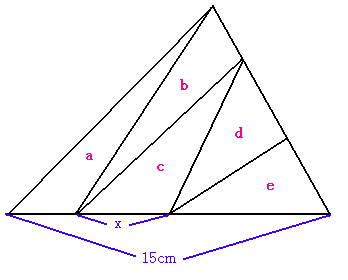
偙傟偼摨堦偺崅偝傪傕偮嶰妏宍偺柺愊偺斾偼丄
偦偺掙曈偺斾偱偁傞偙偲偑暘偐傟偽妝彑両偱偡偹丅
埲壓丄栤戣偺恾柺忋偺埵抲傪傕偲偵丄傕偲偺俆摍暘偡傞
傑偊偺嶰妏宍偵偍偄偰憡懳揑偵忋晹丄掙曈偲掕媊偟傑偡丅
偝傜偵丄嶰妏宍傪偦傟偧傟偺廳怱偑嵍偐傜 a,b,c,d,e 偲偟傑偡丅
傑偢丄嶰妏宍(a)偲嶰妏宍(b+c+d+e)偼栤戣偺恾宍
偵偍偗傞忋晹偺嫟捠偡傞捀揰偐傜偺悅慄傪崅偝偲偟偨応崌偵丄
掙曈偺斾偼偦偺柺愊偺斾偲摨偠偵側傝傑偡丅
崱丄嶰妏宍a,b,c,d,e偺柺愊偼摨堦側偺偱丄椉嶰妏宍偺
柺愊斾偼侾丗係偲側傝傑偡丅偙傟偼掙曈偑侾丗係偱偁傞偙偲偵側傝丄
傕偆堦偮偺嫟捠偺捀揰乮慡懱偺嶰妏宍偵偍偗傞恾柺忋偱偺掙曈
忋偵偁傞乯偼丄慡懱嶰妏宍偺掙曈傪侾丗係偵撪暘偡傞揰偲側傝丄
b+c+d+e 晹暘偺嶰妏宍偺掙曈偼侾俀cm偲側傝傑偡丅
摨條偵丄嶰妏宍(c)偲嶰妏宍(d+e乯傪斾妑偟傑偡丅
掙曈偼丄侾丗俀偲側傝丄栤戣偺x偼丄慜弎偺12cm傪
侾丗俀偵撪暘偡傞偆偪偺侾偵側傝傑偡丅
摎偊偼丄係cm偱偡丅

乮儁儞僱亅儉丗儅僫僥傿乕乯
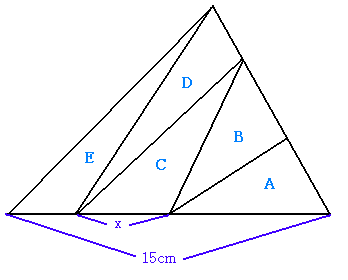
俆偮偺嶰妏宍傪丄戝偒偄嶰妏宍偺塃壓偺捀揰偵嬤偄曽偐傜偦傟偧傟仮A,仮B,仮C,仮D,仮E偲柤慜傪偮偗丄偦傟偧傟偺嶰妏宍偺掙曈傪掙曈A,掙曈B,掙曈C,掙曈D,掙曈E偲屇傇丅
傑偨丄奺嶰妏宍傪崌傢偣偨嶰妏宍偼丄偦傟偧傟偺柤慜傪偮側偘偰柦柤偡傞偲偡傞丅
乮椺丗仮A偲仮B傪崌傢偣偨嶰妏宍偼丄仮AB偲屇傇丅乯
仮C偲仮AB偼掙曈偑摨偠慄忋偵偁傝丄偐偮丄崅偝偑摨偠丅
柺愊偺斾偼侾丗俀側偺偱丄掙曈偺挿偝斾偼侾丗俀偱偁傞丅
丂丂丂丂曈C亊俀亖曈A乨乨乨乨乨乨乨乨乨乨乨乨乮侾乯
仮E偲仮ABCD傕丄掙曈偑摨偠慄忋偵偁傝丄偐偮丄崅偝偑摨偠丅柺愊偺斾偼侾丗係側偺偱丄掙曈偺挿偝偺斾偼侾丗係偱偁傞丅
丂丂丂丂曈E亊係亖曈C亄曈A乨乨乨乨乨乨乨乨乨乮俀乯
戣堄傛傝丄
丂丂丂丂曈E亄曈C亄曈A亖侾俆們倣乨乨乨乨乨乨乨乮俁乯
乮侾乯乮俀乯乮俁乯傛傝丄
丂丂丂丂曈A亖俉們倣丄曈C亖係們倣丄曈E亖俁們倣
摎偊丂丂丂丂 倃亖係們倣

乮儁儞僱亅儉丗嶰妏掕婯乯
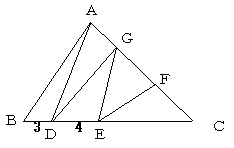
塃恾偺傛偆偵奺揰傪掕傔傞丅
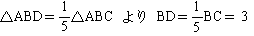
傛偭偰丆俢俠亖15亅3亖12
仮俧俢俠 偵偮偄偰
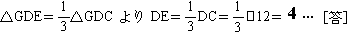

乮儁儞僱亅儉丗儕僫儔僀乯

傑偢丄尦偺嶰妏宍偺崅偝偲1斣嵍偺嶰妏宍偼崅偝偑嫟捠側偺偱丄柺愊傪1/5偵偡傞偵偼掙曈傪1/5偵偡傞昁梫偑偁傝傑偡丅尦偺嶰妏宍偺掙曈偑15們倣偱偡偐傜
丂丂丂15亐5亖3
嵍抂偺嶰妏宍傪彍偔偲
丂丂丂15-3亖12
側偺偱丄巆傝偺掙曈偼12們倣偱暘妱偝傟傞嶰妏宍偑4偮偱偡丅偙偙偱丄塃偺3偮傪尒偰傒傞偲丄尦偺嶰妏宍傛傝傕2/5暘柺愊偺彫偝偄嶰妏宍偑偱偒傑偡丅傛偭偰丄嵟弶偲摨偠傛偆偵丄偙偙偐傜掙曈傪1/3偡傟偽倶偑偱傑偡丅
丂丂丂12亐3亖4
傛偭偰倶=4們倣偱偡丅

乮儁儞僱亅儉丗teki乯

摎偊丂係們倣
亙夝朄亜
堦斣嵍偺嶰妏宍偵偮偄偰偼丄崅偝偼尦偺嶰妏宍偲摨偠偱丄柺愊偼1/5偱偡偺偱丄掙曈偼丂15亊1/5亖俁們倣丂偱偡丅
師偺嶰妏宍偼丄崅偝偼尦偺嶰妏宍偺4/5偱丄柺愊偼1/5偱偡偐傜丄掙曈偼1/4偲側傝傑偡丅
栤傢傟偰偄傞偺偼丄師偺嶰妏宍偺掙曈偱偡偐傜丄崅偝偑3/4丄柺愊偑1/5偺嶰妏宍偺掙曈傪媮傔傟偽偄偄偙偲偵側傝傑偡丅
傛偭偰丄摎偊偼丄15亊1/5亊4/3亖係們倣丂偲側傝傑偡丅
掙曈偺挿偝偼丄嵍偐傜弴偵丄俁丄係丄俉們倣丂偱偡丅

乮儁儞僱亅儉丗壖柺倃乯

柺愊偑俆摍暘偝傟偨偺偱
掙曈偼俁丄倶丄俀倶偵暘偗傜傟傑偡丅
俁亄倶亄俀倶亖侾俆
俁倶亖侾俀
倶亖係
丂丂丂丂丂丂丂丂丂丂丂丂摎偊丂係們倣

乮儁儞僱亅儉丗kiyo乯

恾偺塃壓俀屄暘偺俁妏宍偺掙曈偺挿偝偼丄俀倶偲側傞丅
乮倶+俀倶乯丗侾俆亖係丗俆
侾俆倶亖俇侽
倶亖係
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂摎偊丂係cm

乮儁儞僱亅儉丗柌栭乮傓傛乯乯
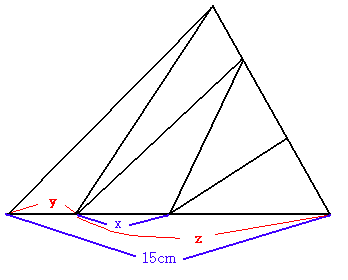
嶰妏宍偺柺愊偼乽掙曈亊崅偝亐俀乿偱偡丅
俆偮偺嶰妏宍偺柺愊偑摍偟偄丒丒丒偲偄偆偙偲偼丄掙曈偵偮偄偰丄媮傔傞挿偝x偺嵍懁乮y偲偟傑偟傚偆乯偺嶰妏宍偲x傪娷傔偨巆傝慡晹偺挿偝乮z偲偟傑偟傚偆乯偱俀偮偺嶰妏宍偵愗抐偱偒傑偡丅
偙偺帪丄崅偝偑堦掕偱偁傞偙偲傪峫椂偡傞偲柺愊斾偑1:4偱偡偺偱丄
y:z亖1:4偐偮y亄z亖15丄偡側傢偪z=12cm偱偡丅
偙偙偱丄嵟弶偺嶰妏宍偱捀揰傪愯傔偰偄偨嶰妏宍傪庢傝彍偔偲丄俁偮偺嶰妏宍偑巆傝傑偡丅
偲偙傠偑丄愭傎偳偲摨偠傛偆偵掙曈傪x偲12-x偱峫偊偨応崌丄崱搙偼柺愊斾偼1:2偱偡偐傜丄x:12-x=1:2偱偡偺偱偙傟傪夝偄偰x=4傪摼傜傟傑偡丅乮徹柧廔椆乯
丂丂丂丂摎偊 x=4乮cm乯

乮儁儞僱亅儉丗mhayashi乯

摎偊丗
掙曈偑 x 偺嶰妏宍偲丆偦偺塃偵偁傞擇偮偺嶰妏宍偺柺愊斾偼 1:2 側偺偱
乽塃偵偁傞擇偮偺嶰妏宍乿偺掙曈偼 2x (cm)偱偁傞丏
傛偭偰堦斣嵍偺嶰妏宍埲奜偺巐偮偺嶰妏宍偺掙曈偼 3x (cm) 偲側傞丏
崱堦斣嵍偺嶰妏宍偲偦傟埲奜偺巐偮偺嶰妏宍偺柺愊斾偼 1:4 偱偁傝丆
屲偮偺嶰妏宍偺掙曈偼 15 (cm) 偱偁傞偙偲傛傝
3x*5/4=15 偑惉傝棫偮丏
傛偭偰 x=4 cm 偲側傞丏

乮儁儞僱亅儉丗棟堦榊朧偪傖傫乯
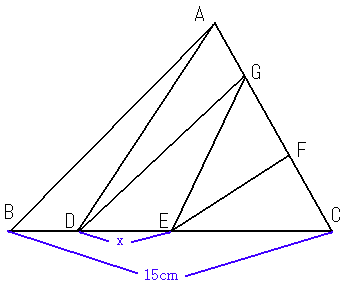
梌偊傜傟偨嶰妏宍傪丄俙俛俠偲偡傞丅俛俠忋偵丄俢丆俤傪偲傝丄俢俤亖倶偲偡傞丅俠俙忋偵丄俥丆俠傪偲傞丅
嶰妏宍俧俢俠偵偍偄偰丄俧俢俤丗俧俤俠亖侾丗俀丂傛偭偰丄俤俠亖俀倶丂
嶰妏宍俙俛俠偵偍偄偰丄俙俛俢丗俙俢俠亖侾丗係丂
傛偭偰丄俛俢丗俢俠亖侾俆亅俁倶丗俁倶
侾丗係亖侾俆亅俁倶丗俁倶丂偙傟傛傝丄倶亖係
丂丂丂丂丂丂丂丂丂丂

乮儁儞僱亅儉丗偨偐傑偮丂傠傠乯

摎偊丂係們倣
5摍暘偟偨嵍抂偺嶰妏宍偼尦偺嶰妏宍偲崅偝偑摍偟偄偺偱掙曈傪侾乛俆偡傟偽傛偔俁
們倣偲側傞丅
師偵丄嵍抂偐傜俀偮暘嶰妏宍傪愗傝棧偡乮尦偺嶰妏宍偐傜俀乛俆愗傝棧偡乯偲巆傝偺
嶰妏宍傪俁摍暘偡傟偽傛偄丅倃傪掙曈偲偡傞嶰妏宍偼巆傝偺嶰妏宍偺崅偝偲摍偟偄偺
偱巆傝偺嶰妏宍偺掙曈乮侾俆亅俁亖侾俀乯傪侾乛俁偡傟偽傛偄偺偱係們倣偲側傞丅
傛偭偰倃偼係們倣丅

乮儁儞僱亅儉丗儌儖儌僢僩戝恇乯
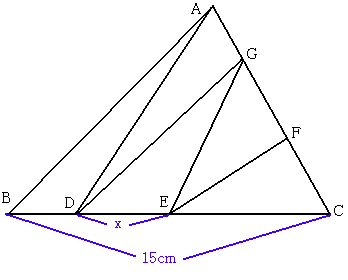
偝偰戞74栤偺夝摎傪憲傝傑偡丅
傑偢梌偊傜傟偨戝偒側嶰妏宍偺3偮偺捀揰傪忋偐傜斀帪寁夞傝偵A,B,C偝傜偵慄暘BC忋
偺2揰傪B懁偐傜D,E丂偦偟偰慄暘CA忋偺 2揰傪C懁偐傜F,G偲偍偒傑偡丅
偙偺帪 嶰妏宍ABC偺慄暘BC傪掙曈偲偟偨崅偝傪2Hcm偲偟傑偡丅
嶰妏宍ABC=15亊2H亐2=15Hcm2偱偙傟偑摍偟偄彫偝側嶰妏宍5屄暘偱偡偐傜彫偝側嶰妏
宍偺柺愊偼15H亐5=3Hcm2偱偡丅
師偵嶰妏宍DCG偲嶰妏宍DEG偵拝栚偡傞偲偦傟偧傟偺柺愊偼嶰妏宍DCG=9Hcm2
嶰妏宍DEG=3Hcm2偱偁傝柺愊斾偼嶰妏宍DCG:嶰妏宍DEG=3:1偱偁傞丅偙偙偱嶰妏宍DCG
偲嶰妏宍DEG偱偦傟偧傟DE,DC傪掙曈偲峫偊傞偲偦偺崅偝偼嫟捠偩偐傜DE:DC=1:3傛偭
偰DC=3xcm偲側傝傑偡丅
摨條偵嶰妏宍BDA偲嶰妏宍DCA傪峫偊傞偲偦傟偧傟偺柺愊偼嶰妏宍BDA=3H cm2
嶰妏宍DCA=12Hcm2偱偁傝柺愊斾偼 嶰妏宍BDA:嶰妏宍DCA=1:4偱偁傞丅
偙偙偱嶰妏宍BDA偲嶰妏宍DCA偱偦傟偧傟BD,DC傪掙曈偲峫偊傞偲偦偺崅偝偼嫟捠偩偐
傜BD:DC=1:4傛偭偰BD=3x/4cm偲側傝傑偡丅
埲忋傛傝BC=BD亄DC= 3x/4亄 3x=15x/4=15傪夝偒x=4cm
傛偭偰媮傔傞挿偝x偼4cm偱偡丅

乮儁儞僱亅儉丗WU乯

掙曈侾俆們倣偵慡偰掙曈傪偦傠偊偨俆偮偺摍愊嶰妏宍傪彂偗偽丆
偦偺掙曈偼俁們倣偵側傞偼偢丏堦斣嵍偺嶰妏宍偼偙傟偲崌抳偡傞丏
廬偄丆堦斣嵍偺嶰妏宍傪彍偄偨掙曈侾俀們倣偺嶰妏宍偺拞偺
係偮偺摍愊嶰妏宍偺栤戣偵抲偒姺偊傜傟傞丏
偙傟偲摨條偵丆塃偺曈傪掙曈偲偟偰峫偊偨帪丆堦斣嵍偺嶰妏宍
乮尦偺恾偱偼嵍偐傜俀斣栚乯偑侾乛係偺嶰妏宍偵憡摉偡傞偐傜丆
掙曈侾俀們倣偺塃偺俁偮偺摍愊嶰妏宍偺栤戣偵抲偒姺偊傜傟傞丏
俁偮偺嶰妏宍偺掙曈傪懙偊傞帠偵傛傝
丂丂丂倶亖侾俀乛俁亖係乮們倣乯
偑媮傔傜傟傞丏

乮儁儞僱亅儉丗Banyanyan乯
崅偝偺摍偟偄嶰妏宍偺掙曈偺斾偼丄柺愊斾偲摍偟偄偐傜丄恾傛傝丄
俛俢丗俢俠亖仮俙俛俢丗仮俙俢俠亖侾丗係
俢俤丗俤俠亖仮俥俢俤丗仮俥俤俠亖侾丗俀
傛偭偰丄俢俤亖俛俠亊係乛俆亊侾乛俁亖侾俆亊侾乛侾俆亖係們倣

乮儁儞僱亅儉丗岼偺柌乯
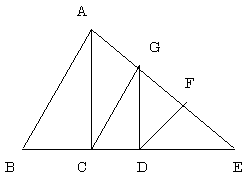
奺揰傪塃恾偺條偵偲傝丄奺乆偺柺愊傪S偲偡傞丅
崱CD偑倶偱偁傞偺偱丄嚈CDG偲嚈DEG偺柺愊斾傛傝DE偼俀倶偲側傞丅
場偭偰丄BC偺挿偝偼15亅俁倶丄CE偺挿偝偼俁倶偱偁傞丅
枖丄嚈ABC偲嚈ACE偺柺愊斾偼侾丗係偱偁傞偐傜丄
(15亅俁倶)乛俁倶丂亖侾乛係偑惉傝棫偮丅
偙偺曽掱幃傪夝偒丄倶亖係傪摼傞丅
場偭偰丄媮傔傞挿偝偼係cm偱偁傞丅

乮儁儞僱亅儉丗yokodon乯
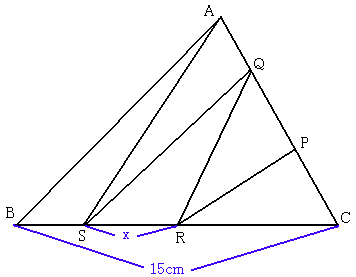
恾偺嶰妏宍傪仮俙俛俠偲偟丄曈俙俠忋偵揰俹丄俻乮捀揰俠偵嬤偄曽偑俹乯丄曈俛俠
忋偵揰俼丄俽乮捀揰俠偵嬤偄曽偑俼乯偑偁傝丄仮俠俹俼丄仮俹俻俼丄仮俼俻俽丄仮俙
俻俽丄仮俙俛俽偺柺愊偑慡偰摍偟偔丄慄暘俼俽偺挿偝偑 x 偱偁傞偲偟傑偡丅
丂恾偐傜丄捈偪偵仮俼俻俠偲仮俼俻俽偺柺愊斾偑俀丗侾偱丄柺愊斾偑掙曈偺挿偝偺斾
偵摍偟偄偙偲偐傜丄俠俼亖 2x 傪摼傑偡偹丅傑偨丄摨條偵仮俙俠俽偲仮俙俛俽偺柺愊
斾偑係丗侾偱偁傞偙偲偐傜丄俠俽亖15亊4/5 亖12 (cm) 偱偡丅
丂懠曽丄俠俽亖俠俼亄俼俽亖 3x 偱偡偐傜丄3x 亖 12 丅偙傟傪夝偄偰丄x 亖 4 (cm)
乧(摎) 傪摼傑偡丅

乮儁儞僱亅儉丗僋儔僀僶乕乯

嶰暘妱偝傟偨掙曈偺嵍曈偺挿偝偼3cm丄側偤側傜偦傟傪掙曈偲偡傞嶰妏宍偼慡懱偺屲暘偺堦偺柺愊傪桳偡傞偐傜丅倶傪掙曈偲偡傞嶰妏宍偼丄嶰暘妱偝傟偨巆傝偺曈傪掙曈偲偡傞嶰妏宍偺擇暘偺堦偺柺愊傪桳偡傞丅愭偵媮傔偨3cm傪15cm偐傜尭偠傞偲12cm丅倶偼丄偦傟傪嶰摍暘偟偨抣傪帩偮備偊倶亖4丅

乮儁儞僱亅儉丗傗側偣乯
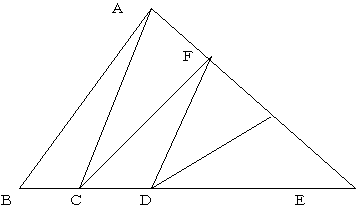
梌偊傜傟偰偄傞忦審偐傜
仮俙俛俠偲仮俙俠俤偺柺愊斾偼侾丗係偵側傝傑偡丅崅偝偑摨偠側偺偱
曈俛俠偺挿偝偼俛俤乮侾俆乯亐俆亖俁們倣
師偵仮俠俢俥偲仮俢俥俤偺柺愊斾偼侾丗俀偵側傞偺偱摨偠傛偆偵
曈俠俢乮倃乯偺挿偝偼曈俠俤乮侾俆亅俁亖侾俀乯亐俁亖係們倣
摎偊倃偺挿偝偼係們倣

乮儁儞僱亅儉丗僗儌乕僋儅儞乯

堦斣嵍抂偺嶰妏宍偺掙曈偼丄15*1/5=3
巆傝偺掙曈偼丄柺愊偺摍偟偄嶰妏宍偑3屄側偺偱丄媮傔傞挿偝偼丄
乮15-3乯*1/3=4丂們倣丂両丂偵側傝傑偡偹丅

乮儁儞僱亅儉丗Y,M乯


乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
摎偊偼係cm偱偡丅
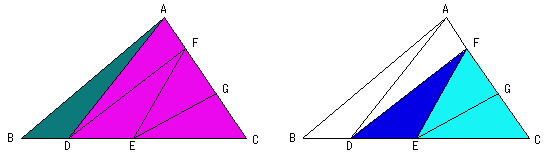
偙偺栤戣偺梫揰偼丄亀捀揰偐傜懳曈偵堷偄偨慄暘偱嶰妏宍傪俀偮偺晹暘偵暘偗偨偲偒丄柺愊偺斾偲暘妱偝傟偨曈偺挿偝偺斾偑堦抳偡傞亁偲偄偆偙偲偱偡丅
偮傑傝恾侾偱丄丂仮俷俹倃丗仮俷俻倃亖俹倃丗俻倃丂偱偡丅
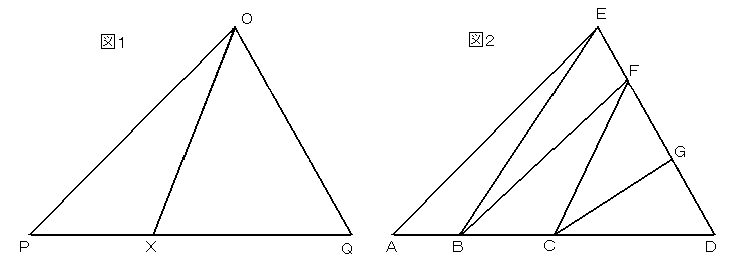
偝偰丄栤戣偼恾俀偱丄俆偮偺嶰妏宍偺柺愊偑摍偟偄偺偱偡偐傜丄 仮俙俛俤丗仮俛俢俤亖侾丗係亖俙俛丗俛俢丂偱偡丅偮傑傝丄俙俛亖俁cm丄俛俢亖侾俀cm偱偡丅
師偵丄仮俛俢俥偵偮偄偰峫偊傑偡丅俁偮偺嶰妏宍偺柺愊偑摍偟偄偺偱偡偐傜丄 仮俛俠俥丗仮俠俢俥亖侾丗俀亖俛俠丗俠俢丂偱偡丅偮傑傝丄俛俠亖係cm丄俠俢亖俉cm偱偡丅
幹懌偱偡偑丄摨偠棟桼偱丄俤俥丗俥俢亖侾丗俀丆俥俧丗俧俢亖侾丗侾丂偱偡偑丄弎傋傞昁梫偑偁傝傑偣傫丅傑偨丄捀揰俤偺埵抲偑偳偙偵偁傠偆偲丄栤戣偼惉棫偟傑偡丅

乮儁儞僱亅儉丗慜敮乯
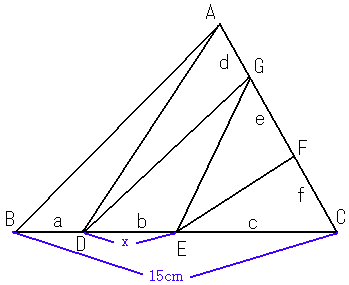
傑偢嶰妏宍傪丄栤戣偺恾偺忋丄嵍壓丄塃壓偺弴斣偵ABC偲偟丄
曈BC忋偺挿偝傪偦傟偧傟嵍偐傜a,b,c乮倐偑摎偺抣乯偲偟丄
曈AC忋偺挿偝傪偦傟偧傟嵍偐傜d,e,f偲偟丄傑偨
曈BC忋偺揰傪嵍偐傜D丄E
曈AC忋偺揰傪嵍偐傜F丄G偲偡傞丅
偙偺偲偒丄佢C傪嫟捠偺妏偲偟偰丄柺愊偺斾偑丄
丂丂丂丂仮FEC丗仮GEC丗仮GDC丗仮ADC丗仮ABC亖侾丗俀丗俁丗係丗俆
傛傝丄偙傟偼丄
丂丂丂丂fc丗乮e+f乯c丗(e+f)(b+c)丗(d+e+f)(b+c)丗(d+e+f)(a+b+c)亖侾丗俀丗俁丗係丗俆
偲側傞丅乮1/2sinC偑慡偰偵嫟捠偵偁傞偺偱徚偟傑偟偨丅乯偙傟傪夝偄偰丄
丂丂丂丂d丗e丗f亖俀丗俁丗係丂丄a丗b丗c亖俁丗係丗俉
偲側傝傑偡丅a+b+c=15傛傝丄倐亖係乮偙傟偑倶偺抣乯偲側傝傑偡丅
偳偆偱偟傚偆偐乮丱丱乯偍偦傜偔曗彆慄側偳偱傕偭偲娙扨偵弌傞偺偱偼
側偄偐偲巚偆偺偱偡偑丄摢偑峝偔偰丒丒丒乮徫乯

乮儁儞僱亅儉丗彫妛柤扵掋乯

摎偊4們倣
塃抂偺嶰妏宍傪堦斣栚偲偟丄悈暯偺曈亖侾丂幬曈亖侾丂偲偟傑偡丅
堦斣栚偺嶰妏宍傑偱偺柺愊偺榓俽乮1乯丄丂擇斣栚偺嶰妏宍傑偱偺柺愊偺榓俽乮2乯丄値斣栚偺嶰妏宍傑偱偺柺愊偺榓俽乮値乯傪
峫偊傞偲丄俽乮1乯丆俽乮2乯丆丏丏丏丆俽乮値乯偺斾偼偦傟偧傟偺悈暯偺曈*幬曈偺斾偱偡丅
偟偨偑偭偰丄
丂丂1*乮0+1乯亖0+1丆1*乮1+1乯亖1+1丆2*乮1+1/2乯亖2+1丆3/2*乮2+2/3乯亖3+1丆8/3*乮3/2+3/8乯亖4+1丆
偺傛偆偵側傝傑偡丅
悈暯偺曈乮1乯丆幬曈乮1乯丆悈暯偺曈乮2乯丆幬曈乮2乯丆丏丏丏偺悢楍偼丄
丂丂丂乮1丆1丆1乯丆1/2丆2/3丆3/8丆8/15丆15/48丆48/105丆丏丏丏
偺傛偆偵側傝
丂丂婏悢斣栚偼乮2*4*丏丏丏*2値乯/乮1*3*5*丏丏丏*乮2値+1乯乯
丂丂嬼悢斣栚偼乮1*3*5*丏丏丏*乮2値-1乯乯/乮2*4*丏丏丏2値乯
偲側傝傑偡乮偨偩偟丄値亖1偺偲偒婏悢斣栚亖2/3丄嬼悢斣栚亖1/2偵懳墳偟傑偡乯丅
悢楍偐傜偲偭偨1丄1/2丄3/8偑悈暯偺曈偺斾偱偡丅偦偺崌寁偼丄
8/8+4/8+3/8亖15/8偲側傝丄暘巕偵15偑尰傟偨偺偱摎偊偼擇斣栚偺暘悢偺暘巕偱偡丅丂

乮儁儞僱亅儉丗Toru乯

堦斣嵍偺嶰妏宍偺掙曈偼侾俆亊侾乛俆亖俁丂栤
戣偺X傪娷傓嶰妏宍偼崅偝偑堦斣嵍偺嶰妏宍偺俁乛係偵側偭偰偄傞偺偱侾俆亊侾乛俆
亊係乛俁亖係乮摎乯偲側傝傑偡丅
丂
偙傟偼堦斒偵掙曈倎偺嶰妏宍傪恾偺傛偆側曽朄偱N摍暘偟偨帪偵傕摨條偵嶰妏宍偵
塃偐傜弴斣偵1,2,3,-------,N 偲斣崋傪偮偗傞偲丄k斣栚偺嶰妏宍偺掙曈偺挿偝偼乮k
偼N偑婏悢側傜婏悢丄嬼悢側傜嬼悢乯
丂
丂丂丂丂倎亊乮(N-1)(N-3)丒丒丒(k亄1)乛N(N-2)(N-4)丒丒丒k乯
偙傟偼偪傚偆偳忋偺嶰妏宍傪
暘巕偵壓偺嶰妏宍傪暘曣偵傕偭偰偒偨宍偱偪傚偭偲偒傟偄偱偡偹丅
傑偨丄媡偵堦斣塃偺嶰妏宍偺掙曈傪侾偲偟偰乮恾偺応崌偼俉偱偡偑乯恾偺傛偆偵嵍
偵岦偐偭偰摍柺愊偺嶰妏宍傪偮偔傝側偑傜丄偳傫偳傫慄傪堷偄偰偄偒丄掙曈偺挿偝傪
塃偐傜倃0,倃1,----倃n偲偡傞偲偙傟偼1,2/4,6/16,20/64,70/256,----,2n俠n乛22n
偲乮俀崁學悢偺拞墰偺抣乯乛乮俀崁學悢偺榓乯偺宍偵側偭偰偙傟傕偒傟偄偱偡偹丅

乮儁儞僱亅儉丗kirkland乯

| 俙孨 | 乽柺愊偑俆摍暘側偺偱丄15們倣偺俆暘偺侾偱俁們倣両両乿 |
| 愭惗 | 乽憡曄傢傜偢丄抁棈揑偩偹偉丅慄暘俥俢丄俢俧丄俧俤傪柍帇偡傞偲乿 |
| 俙孨 | 乽仮俙俛俥偲仮俙俥俠偺柺愊斾偑侾丗係偱崅偝偑摍偟偄偺偱丄掙曈俛俥偲俥俠偺斾傕侾丗係偱偡丅廬偭偰丄俥俠偼俛俠 偺俆暘偺係偱12們倣偱偡丅乿 |
| 愭惗 | 乽偦偆偦偆乿 |
| 俙孨 | 乽師偼丄仮俢俥俧偲仮俢俧俠偺柺愊斾偑侾丗俀偱崅偝偑摍偟偄偺偱丄掙曈俥俧偲俧俠偺斾傕侾丗俀丅廬偭偰丄俥俧偼 俥俠偺俁暘偺侾偱係們倣偱偡両乿 |
| 愭惗 | 乽傛偔偱偒偨偹丄彮擭俙丅乿 |
| 俙孨 | 乽斊嵾幰傒偨偄側屇傃曽偼傗傔偰壓偝偄両偦傠偦傠丄杔偵傕柤慜傪偮偗偨傜偳偆偐偭偰彫搰愭惗偑偍偭偟傖偭偰傞傫偱 偡偗偳丅乿 |
| 愭惗 | 乽俙偩偐傜丄偁懢榊偭偰偄偆偺偼偳偆偩丠乿 |
| 俙孨 | 乽偦傫側儌乕儗僣側柤慜偼僀儎偱偡傛丅偙偙偼偐偭偙傛偔丄傾儞僜僯乕偭偰偄偆偺偼偳偆偱偡偐偹偉丅乿 |
| 愭惗 | 乽壗偱奜恖側傫偩傛両傾儐儉偭偰偄偆偺偼偳偆偩丠乿 |
| 俙孨 | 乽偦傟偠傖偀丄僠儞僷儞僕乕偲摨偠偠傖側偄偱偡偐両乿 |
| 愭惗 | 乽偦傫側偵儗儀儖曄傢傜側偄偩傠両垻俻偭偰偄偆偺偼偳偆偩丠乿 |
| 俙孨 | 乽巰孻偵偝傟偨偔側偄偱偡丅乿 |
| 愭惗 | 乽偳偆傕暥嬪偑懡偄側丅柺搢偩偐傜摉暘偺娫丄俙孨偺傑傑偱偄偭偨傜丠乿 |
| 俙孨 | 乽偦偆偱偡偹丅偟偐偟巆擮両傾儞僜僯乕偼婥偵擖偭偰偄偨偺偵乧乧乿 |

| teki | 偨偐傑偮丂傠傠 | kiyo |
| 彫妛柤扵掋 | 儌儖儌僢僩戝恇 | 屵擭偺偆傝傏偆 |
| 岼偺柌 | 栭傆偐偟偺偮傜偄偍偠偝傫 | Banyanyan |
| 嶰妏掕婯 | 儅僫僥傿乕 | Toru |
| 偽傫偪傖傫 | 忨偺偍偠偝傫 | figo |
| 儅僙偑偒 | WU | 棟堦榊朧偪傖傫 |
| 慜敮 | 僗儌乕僋儅儞 | 傗側偣 |
| yokodon | Y,M | aa |
| 儕僫儔僀 | 僋儔僀僶乕 | 柌栭乮傓傛乯 |
| 僒僟偪傖傫 | nuno | kirkland |
| 壖柺倃 | mhayashi |

杮摉偵偨偔偝傫偺曽偐傜夝摎傪偄偨偩偒傑偟偨丅恾傪揧偊偰偄偨偩偄偨曽傕懡偔丄怱偐傜姶幱偄偨偟傑偡丅
堦尒忦審偑彮側偄傛偆側姶偠傕偟傑偡偑丄乽柺愊傪摍暘偟偰偄傞乿偲偄偆偺偑偐側傝嫮偄忦審偵側傝傑偡丅嶰妏宍偺柺愊傪斾妑偡傞偵偼丄掙曈偲崅偝偺斾傪峫偊傟偽傛偄偲偄偆偙偲偵巚偄偄偨傟偽丄偙偺栤戣偼埬奜僔儞僾儖側傕偺偩偲偄偆偙偲偵偍婥偯偒偩偲巚偄傑偡丅側偐側偐偄偄栤戣偱偡傛偹両両
偙偺栤戣偼俆偮偺嶰妏宍偱偡偑丄偦傟傪堦斒壔偡傞偲偳偆側傞偐丄彫妛柤扵掋偝傫丄Toru偝傫偑峫偊偰偔偩偝偄傑偟偨丅 偦偟偰偙偙偵傕偄傠偄傠側悢妛偺梫慺偑尒偊塀傟偟偰偄傑偡丅墱偑怺偄偱偡偹両

 E-mail
E-mail
 栠傞
栠傞
 top
top