
Weekend Mathematics/コロキウム室/NO.154
| NO.1296 | 2002.10.1. | 水の流れ | ベキ乗の和 |


| NO.1297 | 2002.10.4. | DDT | xのx乗(2) |
xのx乗の不定積分は?の意味は、
 (1)
(1)
が、普通の関数を使って表わされるのかどうか、ということと想像しました。
とりあえず「岩波全書,数学公式Ⅰ」を探してもxxの不定積分式は載っていないので、
厳密な意味での初等関数の範囲では、できないのだと思います
(私は1977年版を使っています。もちろん「できないことの証明」なんかできません)。
ただし、級数の形も許すという条件付きでなら、なんとかなりそうです。
xx=exlogx (2)
です。またeyのテーラー展開は、
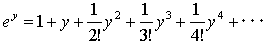 (3)
(3)
なので、y=xlogxとおき、
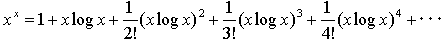 (4)
(4)
を得ます。eyのテーラー展開はもちろん連続関数を表わし、任意のyで一様収束します。
xlogxは0<xでは連続で、 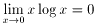 なのでx=0まで連続化できます。よって(4)の右辺は任意のxlogxで、
いいかえれば任意の0≦xで連続関数を表わし一様収束するはずです。
一様収束すれば項別に積分して良いので、
なのでx=0まで連続化できます。よって(4)の右辺は任意のxlogxで、
いいかえれば任意の0≦xで連続関数を表わし一様収束するはずです。
一様収束すれば項別に積分して良いので、
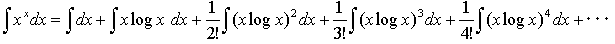 (5)
(5)
となり、結局
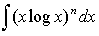 (6)
(6)
の積分に帰着されます。(6)は初等関数で表わせます。
実際、(xlogx)n=xn・(logx)nと分けて考え、部分積分の公式を繰り返し用いるとして、
積分するのをxnの側,微分するのを(logx)nの側と決めておけば、いつかはxnの積分に落ち着きます。
先程の「岩波公式集」によれば、
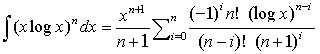 (岩波全書,数学公式Ⅰ,pp.163) (7)
(岩波全書,数学公式Ⅰ,pp.163) (7)
になるそうです。(7)を使えば、(5)は、
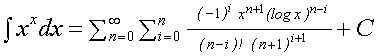 (8) (一部修正10/7)
(8) (一部修正10/7)
と書けます。ここでCは積分定数で、不定積分の印し。(8)は0≦xで連続な関数の積分なので、0≦xで連続関数を表わし、一様収束するはずですが、かなり不細工です。また(4)がxxの最良の展開法であるとも限りません。こういうのって結局、運が大きく、残りほとんど根気で、あとはセンス少しだけですよね。センス皆無でも、運が良ければ行けちゃったりします。私はセンスがないので、いつも、運>根気>センスの順番です。

| NO.1298 | 2002.10.5. | 杖のおじさん | Excelの三角関数(1) |
Excelで、sin、cos、tanの値を求める方法を教えてください。
関数を選択すると、ラジアン値で入力して下さいとメッセージが書いてあります。
どの様にしてラジアン値を入力すればいいのですか?
例えばsin30゚を求めるとき、どの様にすればいいのですか?

| NO.1299 | 2002.10.5. | 浜田 明巳 | Excelの三角関数(2) |
sin30°をセル上で計算するときは,
=SIN(30*PI()/180)
とすればよいです.
PI()/180は角をラジアンに変換する定数です.勿論PI()は円周率のパイです.

| NO.1300 | 2002.10.6. | Junko | ベキ乗の和(2) |
(1)
| Δnk | =(n+1)k-nk |
| =(n+1)n(n-1)・・・(n-k+2)-n(n-1)(n-2)・・・(n-k+1) | |
| =n(n-1)・・・(n-k+2){(n+1)-(n-k+1)} | |
| =k・n(n-1)・・・(n-k+2) | |
| =k・nk-1 |
(2)
| S(Δf)(n) | =Δf(0)+Δf(1)+Δf(2)+・・・+Δf(n-1) |
| ={f(1)-f(0)}+{f(2)-f(1)}+{f(3)-f(2)}+・・・+{f(n)-f(n-1)} | |
| =f(n)-f(0) ・・・(*) |
(1)より、Δnk=k・nk-1
kを(k+1)に置き換えて、
Δnk+1=(k+1)・nk
従って、S(Δnk+1)=(k+1)・S(nk)
| S(nk) | =1/(k+1)・S(Δnk+1) |
| =1/(k+1)・{nk+1-0k+1} ・・・(*)より | |
| =1/(k+1)・nk+1 |
(3)
n3=n3+3n2+n1を示します。
| n3+3n2+n1 | |
| = | n(n-1)(n-2)+3n(n-1)+n |
| = | n3 |
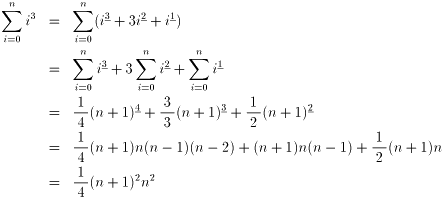
(4)
n4=n4+6n3+7n2+n1だから、
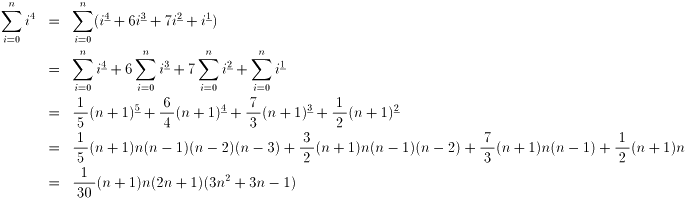

| NO.1301 | 2002.10.6. | イレブンpm | 複素数の定義(1) |
質問です。
複素数の演算においてa,b,c,d∈Rのとき
(a+bi)+(c+di)=(a+c)+(b+d)iと定義されますが、
複素数の演算定義に何故複素数であるa,b,c,dを
使っていいのか。
実数は複素数の部分集合だから
実数の要素は複素数の要素であります。
複素数の加法の定義に複素数である実数を用いることは
甚だ変な事だと思いませんか?

| NO.1302 | 2002.10.6. | イレブンpm | πのπ乗 |
πのπ乗は無理数なのか?

| NO.1303 | 2002.10.6. | イレブンpm | 平方数の逆数の和 |
平方数の逆数の和は何故収束するのか?

| NO.1304 | 2002.10.7. | DDT | 複素数の定義(2) |
答えにくい問いかけだと思います。結局、数学における定義は、内包的か外延的か?ということになるのでしょうか?。
例えば整数Zの定義の場合、自然数NをN={0,1,2,3,4,・・・}だとして、加法の逆演算に対してもNの拡張が閉じるように、Nの対称化N'={・・・,-4,-3,-2,-1,0}をNとは別に生成し、
Z=N∪N'={0,1,2,3,4,・・・}∪{・・・,-4,-3,-2,-1,0}
として、和集合N∪N'の総称名として、整数という言葉を導入します。この時にも、あくまで内包的定義ということにこだわるなら、Nの加法の性質(実際Nの生成原理です)からN'を導くので不合理かもしれませんが、外延的定義の立場では、単にそれぞれ集合として存在可能な2つの集合の和集合に、その総称名を付けただけなので、その名前と内容とは別個のものとみなせます。実際外延的定義では、名前は省略記法であり、その内容は含まれる個々の要素を具体的に観察することで、勝手に意味を汲み取れということになります。だからこそ「問1.問1の答え」のところで書いたように、個々の要素の具体的与えられ方を知らなければ解き方もわからないですし、「ラッセルのパラドックス」のような内包的定義に近い集合の定義も拒否される気がします。確かにこの状況はちょっと逆説的です。そういうわけで「問1.問1の答え」では、意味と記号,記号と対象の間には双対性があるのかと疑ってしまう、と書きました。
いずれにしろ既存の数学の定義は、みな外延的(すでにあるものに名前を付けるだけ)なのでいいのでは?というのが、ここでの漠然とした趣旨です。

| NO.1305 | 2002.10.8. | yokodon | 回転体の体積(3) |
NO.1293の回転体の体積の問いに対する
NO.1294 の BossF さんの解答に、補足で
す(大きなお世話とも言う)。
個人的な好みを言えば、「公式より…」の一言で済ませるよりは、きちんと泥臭い
計算をして結果の正当化をしておくことが重要だろうと思うので(本格的な数学の研
究では、一々を全部証明していたら手間が大変なのでやむを得ないとしても、そうで
ない範囲では、あまりに簡潔を旨とするのは、場合によってはどうかな?と思うので
)、あえてそんなことをしてみるわけです。
先に見通しを立ててしまうなら、すべて本質的には置換積分で解決可能です。
(1)y = x2 - 4x + 5 と y = 2x で囲まれた部分を y 軸の回りに回転させて得ら
れる立体の体積
便宜上、f(x) = x2 - 4x + 5, g(x) = 2x とおきます。
曲線 y= f(x) の閉区間 [1,2] 及び [2,5] における部分の逆関数を、それぞれ x
= x1(y) , x= x2(y) とします。
題意の体積を V とすると、求積の式は以下です。
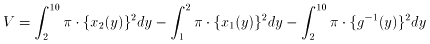
以下、これを変形して“バームクーヘン積分”の形にしてみましょう。
第1項と第2項で y = f(x)、第3項で y = g(x) と置き直してみます。
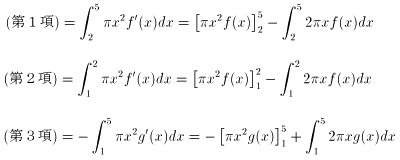
従って、以上をまとめて整理すると、f(1) = g(1) 、f(5) = g(5) に注意して以下
を得ます。
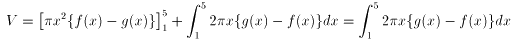
以下、NO.1294 の前半に同じです。
(2)y = x2 - x と y = x で囲まれた部分を直線 y = x の回りに回転させて得ら
れる立体の体積
点P (x,y) を通り y 軸に平行な直線と直線 y = x との交点をRとし、
l = |PR| 、s = |OR| と置きます。
|PQ| = |PR| = l/√2 、t = s - l/√2 、s = √2・x 、l = 2x - x2 です。
求める体積を V とおくと、求積の式は以下です。
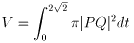
これを変形していきます。
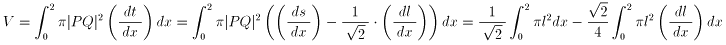
ここで、第2項において x:0→1、1→2 のとき l:0→1、1→0 であることに注意
して変形すると、
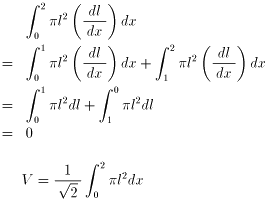
となり、“傘型回転体”の“公式?”を得ます。以下、NO.1294 の後半に同じです。

| NO.1306 | 2002.10.8. | yokodon | 平方数の逆数の和(2) |
収束することを示すだけなら、数列
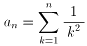
に対して、
『上に有界な単調増加列は収束する』という定理を適用すれば容易です。具体的には
、任意の自然数 n に対して以下の2つが成り立つことを示すことですね。
この無限和の値がπ2/6 であることを示すのは、それなりに大変です(でも確か
、ゼータ関数がらみの過去ネタであったような…)。

 E-mail
E-mail
 戻る
戻る