Weekend Mathematics／問題／問題53
５３．蒸気機関車の問題
長さ150mの蒸気機関車が円となるように敷いたレールの上を走っている。 列車の長さの２倍に等しい距離を進む毎に、その方向が３０度変わるものとする。 レールが敷かれている円周の半径を求めよ。
あそびの数学／へフォード＋バブ著／三橋重男訳／東京図書
（ペンネ−ム：やなせ）
列車の長さの２倍の距離を進んだときに
角度が３０度変わるんですよね。
円１周の角度は３６０度です。
でもって、３６０÷３０＝１２
つまり円周は列車の長さの２４倍になります。
列車の長さ１５０ｍ×２４＝３６００ｍ
となると、その円の半径は
３６００÷３．１４÷２＝５７３．２４８になります
（ペンネ−ム：kiyo）
レ−ルの長さ (150×2)×360/30=3600
半径をrとする。
2×π×ｒ=3600
r=1800/π
答え 1800/π m
（ペンネ−ム：judas）
列車の2倍の距離、すなわち300m走るごとに向きが30度変わるのだから、
同じことを12回繰り返せば30×12=360で元の向き、すなわち一周してもとの位置に戻
る。
円周は300×12=3600だから、半径は1800/3.14≒573.25となる。
（ペンネ−ム：楓 ）
列車の長さは150Ｍ、2倍の距離を進むと30度方向を変える事から、
円周は、
150×2×（360÷30）＝3600
3600Ｍとなります。
よって円の半径は
3600÷3、14＝1146、49(直径）
1146、49÷2＝573、24
Ａ573、24Ｍ（小数点第三位は切り捨て)
となります。
また、π をつかうと、
3600/2π
となります。
（ペンネ−ム：ろんじゃー ）
つまり機関車が３００メートル進めば、向きが３０度変わると言うことで
ある。
結局３００×１２メートル進めば、３６０度、つまり一周したことになる。
よって
３００×１２＝２πr
いま流行りのπ＝３計算すると
r＝６００（メートル）
（ペンネ−ム：かつ ）
まず列車の長さの２倍なので、列車は３００メートル進んだことになります。
そのときに進む向きが３０度変わったということなので、ベクトルでいるところの速
度ベクトルの向きが３０度変わったということです。速度ベクトルの向きは接線と同
じなのでその点における半径と直交していることになります。（表現がよくないかも
・・・）
つまり始点のときの速度ベクトルと動いたあとの速度ベクトルとの変化の角度は円の
中心角の角度と一致します。
よって円の円周を求めることができます。
３００×１２＝３６００
円周がわかったので、半径を求めます。
３６００/π×1/2＝1800/π
となります。
（ペンネ−ム：夜ふかしのつらいおじさん ）
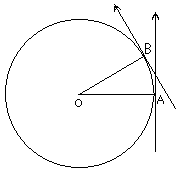
答えは、約573mです。
蒸気機関車がＡからＢに来たとき
接線方向が３０度変わったということは
中心角ＡＯＢが３０度ということです。
弧ＡＢの長さが300mなら円Ｏの円周は
300×（360度／30度）＝3600m
だから、半径は
3600／2π＝1800／π＝約573m
（ペンネ−ム：浜田 明巳）
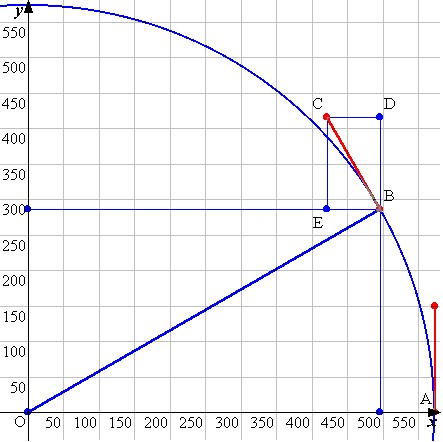
図において，ＯＡ＝ｒ（ｍ）とする．
∠ＣＢＤ＝３０°，
∠ＯＢＣ＝∠ＥＢＤ＝９０°，
ＥＢ//ＯＡ
であるから，
∠ＡＯＢ＝∠ＥＢＯ＝∠ＣＢＤ＝３０°
弧ＡＢ＝２πｒ×∠ＡＯＢ／３６０°なので，
１５０×２＝２πｒ×３０／３６０
∴ｒ＝１８００／π
故に半径は１８００／πｍである．
（ペンネ−ム：けんたん）
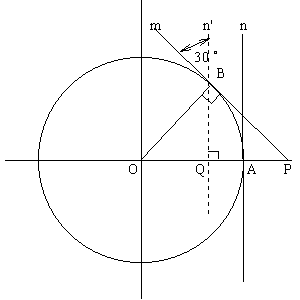m,nはそれぞれ点A,Bを通る接線
弧ABの長さは300m
Pは直線mとOAの延長線が交わる点
QはBからOAに下ろした垂線とOAとが交わる点
（解答）
左図の通り、作図を行うと、mとOB、nとOAはそれぞれ直角に交わっている。
条件より ∠QBP=30°
| ∴∠BPQ | =180°−∠BQP−∠QBP |
| =180°−90°−30° | |
| ∴∠BOP | =30° |
（ペンネ−ム：yutaka）
機関車の長さが１５０メートルということは２倍の長さは３００メートル。
３００ｍ進むごとに列車の向きが３０度変わると言うことは３０
０ｍすすんだ点と進む前の点を円の中心から見た角度が３０度になるということである。
したがって円周はその１２倍の長さの３６００ｍと
なり、円の半径は３６００／２πとなり１８００／πメートルとなる。
（ペンネ−ム：高橋 道広 ）
解１
360度方向が変化したときは蒸気機関車は、300ｍ×360/30=3600m進んでいる。
よって、半径3600/２π=1800/π m
解２
y=ｒ・sinωtとすると y'=rω・cosωt つまり速度ベクトルの角速度と円運動の角速度は
一致する。
300ｍ進んだときの角の変化がπ/6ラジアンなので、半径は
300÷π/6=1800/π ｍ
解３
出発点Aでの接線と、300m進んだ点Bでの接線の交点をCとする。
円の中心をOとし、四角形OACBは円に内接するから、角AOB=30度となる。
以下略
（ペンネ−ム：柿本 浩）
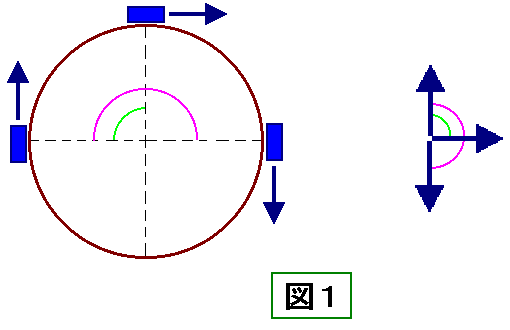
※ある時点での機関車の先頭車両が向いている方向を、
その時点における機関車の進行方向と見なす事とする。
機関車が円周の1/4の距離を移動すれば、
進行方向は90度変わって最初の方向と垂直に、
円周の1/2の距離を移動すれば、
進行方向は180度変わって最初の方向と正反対となる。
（図１参照 ※図は全て機関車がレール上を時計回りに回る場合のもの）
つまり進行方向の変化は、機関車が進んだ円弧の角度と見なす事ができるため、
進行方向が30度変化するという事は
30/360 = 1/12 で、機関車は最初の位置から1/12周の距離だけ
離れた地点にある、という事になる。
（ただし、1周回ると進行方向は360度変化して元に戻るため
機関車がレールの上を何周したかまでは判断できない。）
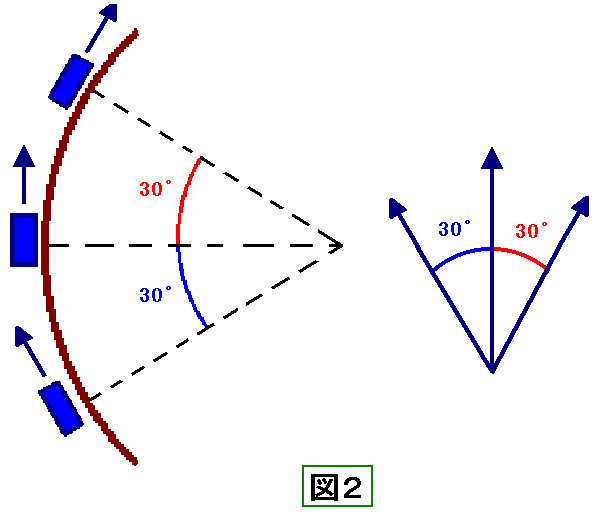また、問題文には機関車がレール上を回る向き、
進行方向が左右どちらに変化するのか等は明記されていないため、
機関車が最初の位置より1/12周だけ進んだ位置にあるのか
1/12周だけ遅れた位置にあるのかは判断できない。（図２参照）
これらの事を踏まえ、進行方向が最初と30度ずれるパターンは
●機関車が1/12周の距離を進んだ場合
この場合、1/12周で 150×2 = 300m なのだから
1周の距離は 300×12 = 3600mとなり
半径を r とすると 2πr = 3600 ∴r = 1800/π[m] となる。
●機関車が11/12周の距離を進んだ場合
この場合、1周の距離は 300×12/11 = 3600/11[m] で
半径 r は 2πr = 3600/11 ∴r = 1800/11π[m] となる。
●機関車が13/12周（1周と1/12）の距離を進んだ場合
この場合、1周の距離は 300×12/13 = 3600/13[m] で
半径 r は 2πr = 3600/13 ∴r = 1800/13π[m] となる。
●機関車が23/12周（1周と11/12）の距離を進んだ場合
この場合、1周の距離は 300×12/23 = 3600/23[m] で
半径 r は 2πr = 3600/23 ∴r = 1800/23π[m] となる。
そして、300mが25/12周（2周と1/12）の距離に当たると考えるならば
1周のレールの長さは 300×12/25 = 144m となり
機関車の長さ150mよりも短くなってしまうためこのような場合は有り得ない事が分かる。
よって、問題のレールの半径として考えられるのは
1800/π[m],1800/11π[m],1800/13π[m],1800/23π[m] のいずれかとなる。
最初は
「なんだ、300mで30度なら、1周は3600mだな。単純、単純。」
なんて思ってましたが、突っ込んで考えてみると
４通りのパターンがあるんですね。
左右どちらにずれたかが明示されていないならば、
30度ずれるも、330度ずれるも同じ事。
23/12周の場合、1周約156.5mのレールに
150mの長さの機関車がのる事になりますが
有り得ないとは言い切れない、と。
私の考えすぎですかね(^^；
（ペンネ−ム：ねこ）
円弧長の３００ｍがπ／６[rad]に相当する。
radianは半径と円弧長の比なので、
３００／ｒ＝π／６
が成り立つ。よって、
ｒ＝１８００／π[m]（≒５７３[m]）
（ペンネ−ム：ＤＤＴ ）
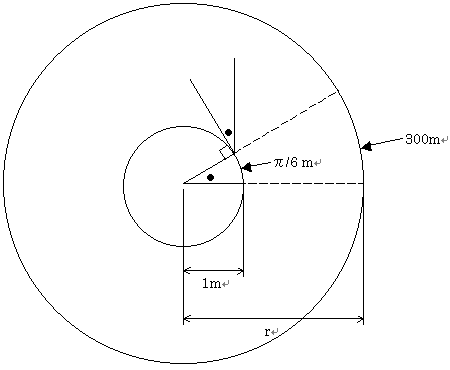
●：π/6 rad ＝ 30°
r ： 1m ＝ 300m ： π/6 m
r ＝ 1m×300／(π/6) ＝572.958 m
| 高橋 道広 | 夜ふかしのつらいおじさん | やなせ |
| yutaka | 浜田 明巳 | けんたん |
| judas | ねこ | 柿本 浩 |
| kiyo | 楓 | DDT |
| かつ | ろんじゃー |
今回の問題は簡単でしたか？
逆に裏があるんじゃないかって深読みされた方もいたようです。
この問題をきっかけに弧度法の話をしようかな、と思ったのです。
その導入は、ねこさん、ＤＤＴさんがしてくださいました。
ここで改めて、弧度法を紹介します。
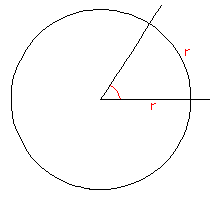
扇形の弧の長さと、中心角が比例するということをまず確認してください。
このことを利用して、
半径ｒの円に対して弧の長さがちょうどｒになるときの中心角を１(ラジアン)
と定義します。
弧の長さで定義することから、弧度法と呼ぶわけです。
これに対して、１周３６０度、言い換えれば１周の１／３６０を１度として角度をはかる方法を
度数法と呼びます。
私達の生活の中では、度数法が定着しています。
ですから最初に弧度法に出会ったとき、なんでこんなことするんだろう？ って思った人も多いのではないかと思います。
私もそう思いました。微積分を勉強していくと、弧度法の良さを実感します。
関数を微分したり、積分したりする際に、余分な定数がつかないのです。
（それは対数関数において、底を自然対数ｅにとるというのも同じですね。）
でもよくよく考えてみると、半径と弧の長さとの比で角度を表すという相対的な定義だから
こそなのだなあということに気づきます。
そして、弧度法の定義の方がむしろ自然に思えてきます。
度数法の方が、意図的？ 誰がいつ１周を３６０度って決めたのでしょう？
場合によっては１周が１００度でもよかったのかもしれない。(ちょっと不便な気もしますが・・・)
１０進法が主流なのに、なぜ角度のはかり方は違うのでしょう？
１周はなぜ３６０度なのか？
人類が農耕生活を始めた頃、自然の観察が必要であった。 季節があることに気づき、１年がほぼ３６０日であると考えるようになった。 この３６０日を円周上に配置したので、３６０度になったといわれている。
今日の度分秒の元祖はプトレマイオス(Ptolemaios)で、「アルマゲスト」は三角法の出発点である。
彼は円の半径を６０にとり、これに等しい長さの弦のなす角を６０度にした。
１年が３６０日であることと、プトレマイオスの考えがあいまって、１周が３６０度になったようである
（仙田章雄著、日本実業出版社、「数とグラフの雑学事典」より）
柿本 浩さんの深読みには、うーんて思っちゃいました。
そうですよね、確かに、そうですよね。
厳密性を追求する数学の問題としては曖昧だったかもしれませんが、
具体的にイメージできるということも大切だと思いますのでご勘弁。
E-mail
戻る
top