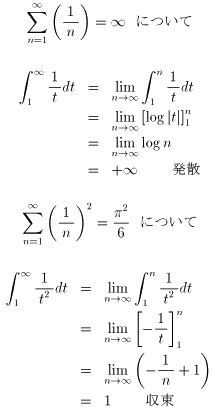
Weekend Mathematics/コロキウム室/NO.137
| NO.1172 | 2002.3.11. | Junko | 級数の実用的な収束判定(3) |
NO.1168で挙げられている例について、確かめてみました。
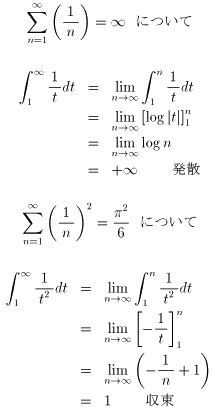
「Σf(n)の収束、発散は∫f(t)dtのそれに帰着されます。」

| NO.1173 | 2002.3.11. | Kernighan | 級数の実用的な収束判定(4) |
はい。もちろんΣf(n)=∫f(t)dtという意味ではありません。
積分と比較する方法はよく使われますが、たいていの場合、
図を描いてみてf(t)のつくる面積のほうが小さい・大きいという
説明がなされ、数式を使って示すことはあまりないようです。
そのためか、昔は、この方法はなんとなく胡散臭く感じていましたが、
最近ちゃんとした証明を読んで、ようやく納得しました。

| NO.1174 | 2002.3.13. | DDT | 二項分布から正規分布へ(1) |
先日の話です。私の所属する部署では安全な斜面に亀裂変位計などの計測器を
ぺたぺたと貼り付けて、実験フィールドで斜面監視(?)を行っております。
そこで問題になるのは得られた計測値時系列から、監視中(?)の斜面が危険かどうかを、
どうやって判定するかです。最も安易な案が出ました。
「斜面が動いてないなら(実際動いてないです。誰が見ても安全な斜面ですから)
計測値は一定だ。だったら全時系列の平均μと標準偏差σを出して、
平均から2σ以上離れた計測値が出た時点でアラームしたら?」
「オー!」一同安易に納得しました。
「で?、分布はどうするの?」「当然正規分布でしょ?」「不安だからちょっと調べない?」
一同、昔の教科書とインターネット検索ネタを持ちよると、こんなんなりました。
「正規分布って二項分布で事象数nを無限大にした奴なんだ」「ふ〜ん」
「ポアソン分布は事象の確率pが小さくて、nが大きい時に使うんだって」
「ふうう〜〜ん」「グンベル,指数,ワイブル分布は、パラメーターのとりかたで正規分布に近づく
って書いてあるぞ」「じゃっ!、二項分布がわかればいいんだ!!」
インターネット検索ネタによれば、サイコロをn回ふるとき、5の目がr回出る確率は・・・、
P(r)=nCr・pr(1−p)n-r,p=1/6
一同、二項分布を完璧に理解した気分になりました。
では、平均μ(メートル)の計測平均値から2σ(メートル)はずれた計測値は、
サイコロの5の目が2σ(メートル)回出た確率?・・・???。
ここで全員の脳みそがフリーズしたのはいうまでもありません。
どなたか妥当な解釈を教えて下さい。お願いします。

| NO.1175 | 2002.3.16. | Junko | 3次関数の係数条件(2) |
f(x)=y = ax3 + bx2 +cx(a ≠ 0)とおく。
P(α,f(α))、Q(β,f(β))とおく。
2点P、Qにおける接線の傾きが等しいことから、
f’(α)=f’(β)
f’(x)=3ax2 + 2bx + c なので、
3aα2+2bα+c=3aβ2+2bβ+c
これより、
α+β=−2b/3a ・・・(1)
次に、点Pにおける接線lの傾きは、f’(α)=3aα2+2bα+cであるから、
これと直線y=xで対称な直線l’の傾きは、
1/f’(α)=1/(3aα2+2bα+c)
一方、直線PQの傾きは、
{f(α)−f(β)}/(α−β)=a(α2+αβ+β2)+b(α+β)+c
直線l’と直線PQが垂直であることから、
{a(α2+αβ+β2)+b(α+β)+c}/(3aα2+2bα+c)=−1
(1)を用いて、βを消去すると、αについての2次方程式となる。
18a2α2+12abα+9ac−b2=0
この2次方程式が実数解をもてばよい。従って、
D/4=(6ab)2−18a2(9ac−b2)≧0
これより、
b2−3ac≧0

| NO.1176 | 2002.3.17. | 水の流れ | 格子点である正三角形(1) |
太郎さんは大学の数学科を希望する生徒がいたとき、
推薦入試でどんな論文が出題されるか、
面接でどんな口頭試問があるか予想したいと考えています。ここで、問題です。
問題1:
xy平面上の点で、
x座標もy座標も整数であるような点を平面上の格子点または整数点と言います。
平面上の格子点から3点を選んで結び、正三角形にできるか。論じてください。

| NO.1177 | 2002.3.17. | yokodon | 格子点である正三角形(2) |
ちょっと考えてみました。
平行移動により、3頂点のうち1個が xy 平面の原点であるとしても構いませんね(詳細後述)。
あとの2点を ( m, n ) および ( p, q ) とします。
件の3頂点が正三角形をなすとすると、以下の式が成り立ちます。
但し、R(α) は
、反時計回りを回転角の正方向とする回転行列を表します。
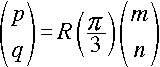
これより、以下の関係式を得ます。
p = (m - √3・n)/2 ,q = (√3・m + n)/2
m および n が整数の時、√3 は無理数なので同時に整数にはなりません。
また、[1] 式で“π/3”を“-π/3”に交換しても、全く同様の議論になります。
(補足:因みに、3頂点のいずれも原点とは限らないことを念頭に置いても、残る1
点を ( a, b ) として、[1] 式で“p”→“p - a”、“m”→“m - a”、“q”→“q
- b”および“n”→“n - b”として議論しても同様の結果になります。仮定より、a
,b,m,n,p,q はいずれも整数ですから、2頂点を結ぶベクトルの成分もまた整数であ
り、従って x 座標及び y 座標の差が整数であることが本質的であるので、「平行移
動により、3頂点のうち1個が xy 平面の原点であるとしても構」わないわけです)
よって、結論は「不可能」です。…(答)
#このくらいだと、論文試験でなくとも、国公立の通常の数学の2次試験で出るかも
知れませんよ(さすがに、1次変換は現行では高校の範囲外ですが、複素平面におけ
る点の回転移動を考えれば、本質的には同じですから)。

| NO.1178 | 2002.3.17. | Junko | 格子点である正三角形(3) |
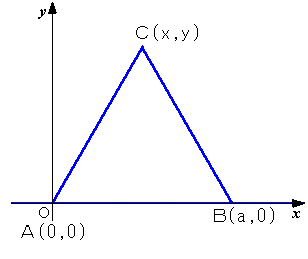
正三角形ABCを、点Aが原点と重なるように、さらにABがx軸と重なるように配置する。
A(0,0)、B(a,0)、C(x,y)とおく。
三角形ABCは正三角形なので、
x=a・cos(π/6)=(1/2)a
y=a・sin(π/6)=(√3/2)a
これより、aとyが同時に整数(有理数にすら)にはならない。
従って不可能。

| NO.1179 | 2002.3.19. | ニースケンス | 格子点である正三角形(4) |
むかし本で読んだ方法をご紹介します。
題意の三角形が存在したとして、それを△ABCとします。
Aを中心として△ABCを2倍拡大し、B, Cの移り先をそれぞれ
D, Eとすると、△ADEも正三角形であり、D, Eも格子点です。
BはADの中点ですからAD⊥BEです。すなわち、AB, BE上の格子点は
同じ間隔で並んでいますから、A, EがBから数えてそれぞれ
p, q番目の格子点とすると、BE/AB=q/p=√3となって矛盾です。

| NO.1180 | 2002.3.20. | wasmath | 格子点を頂点とする正三角形(5) |
「格子点である正三角形」は日本語がおかしいので,
勝手に「格子点を頂点とする正三角形」とさせていただきました。
問題は,正三角形にこだわらず,
「格子点を頂点とし,60度の内角をもつ三角形は存在しない」ようです。
三角形を平行移動させ,内角60度の頂点が原点にくるようにします。
必要ならば90度回転させることにより,
残りの頂点はy軸上にないとしてさしつかえありません。
三角形の頂点を(0,0),(a,b),(c,d) (a≠0,c≠0)とし,
tanα=b/a,tanβ=d/cとおきます。加法定理より
tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)=(bc-ad)/(ac+bd)
となり,a,b,c,dは整数ですから,tan(α-β)は有理数です。
ところが,tan(±60°)=±√3は無理数ですから一致しません。 (証明おわり)
NO.1179(4)の証明はあざやかですね。
正三角形に限定すれば,それ以外にも
a2+b2=c2+d2=(a-c)2+(b-d)2
が非自明解をもたないことを示す方法も,中学の範囲で証明できます。
a,b,c,dがすべて偶数ならば,相似比 1/2を考え直せばよいので,
少なくとも一つは奇数の場合だけ考えれば十分です。
ところが,a2+b2=c2+d2より,aとbの少なくとも一方,
cとdの少なくとも一方が奇数となります。上式を変形すると
a2+b2=2(ac+bd)=c2+d2
となり,2(ac+bd)が偶数なので,結局a,b,c,dすべて奇数となります。
すると,a2+b2とc2+d2はともに4で割れない偶数で,ac+bdは偶数となるので矛盾します。
(証明おわり)
NO.1178(3)の証明は,x軸に平行なものの中にはないことを示しているだけ,
のような気がしますが・・・。

| NO.1181 | 2002.3.24. | yokodon | 二項分布から正規分布へ(2) |
測定値 x が正規分布 N(μ,σ2) に従うものとして、正規分布表から数値計算す
ると、x が区間 μ-2σ≦ x ≦μ+2σ の外にある確率は、約 0.045 です。恐らく斜
面上のある定点の変位の大きさを測定しているのだと思いますが、まぁ恐らく正規分
布で(1次近似としては)問題ないのではないでしょうか?
因みに、二項分布の式から正規分布を導くやり方ですが、
P(r) = nCr・pr・qn-r , p + q = 1 ・・・[1]
の式で、
t = (r - np)/√(npq)
とおくと、この t は n が充分大きいとき正規分布 N(0,1) に従うことを示すことが
出来ます
(ところで、E(r) = np ,V(r) = npq でしたね;この期待値 E(r) は、
二項分布に従うある事象を n 回反復したときの、問題にしている事象が現れる回数
の期待値です;統計学の流儀にきちんと従うなら、ベルヌーイ試行に従う事象の確率
分布が二項分布である、という感じでしょうか)。
実際、[1] の第1式を変形すると、スターリングの公式を用いて、
P(r) ≒ 1/√(2π)×√(n/r(n - r)) ×(np/r)r・(nq/(n - r))n-r ・・・[2]
とできます。
なお、スターリングの公式は、以下です。
(n を自然数として)n! ≒ nn・exp(-n)・(√(2πn) + o(1/n))
さて、[2] 式の r を含む3つの項に関して、対数計算をします。結果だけ示しま
すが、以下のようになります(ここで、ln(1 + x) のマクローリン展開の公式を用い
ています)。
ln(np/r)r≒ -√(npq)・t - 1/2・qt2
ln(nq/(n - r))n-r ≒ √(npq)・t - 1/2・pt2
ln√(n/r(n - r)) ≒ -1/2・{ln(npq) + [√(q/np)・t - 1/2・q/np・t2] + [√(p/
nq)・t - 1/2・p/nq・t2]}
よって、以上をまとめて [2](の両辺の対数を取ったもの)に代入し、n → ∞ の
極限にて整理すると、
lim ln(P(r)) = -ln√(2π) - 1/2・ln(pq) - 1/2・t2
となり、従って、
lim P(r) =1/√(2πpq)・exp(-1/2・t2)
となります。
この結果は正確に N(0,1) を与えるものではないんですけど、2項分布が正規分布
に漸近する事実は「ド・モアブル-ラプラスの定理」として知られています(計算間
違いがあったら、ゴメンナサイ)。
というわけで、最後のフリーズしたところに関してお答えすると、結論として、こ
こで p= 1/6 として二項分布 P(r) が漸近して正規分布 N(np,npq) に“漸近”する
とき、その分布はあくまで「さいころの5の目の出る回数の分布」であるわけです(
言い換えれば、さいころの5の目の出る回数が、ここで問題にしている確率変数であ
ると言うことです)。
斜面上の定点の変位 x の測定値の従う確率分布を正規分布とみなすのは、あくま
で x が本来ある別の確率分布に従うものとして、その測定例数が充分大きければ、
その確率分布がある正規分布に漸近することから言えるのだろうと考えます。
蛇足ながら、二項分布からポアソン分布を導くのは (1 + 1/x)x → e(x → 0 の
とき)を用いると、比較的容易に出来ます。計算練習にいかがでしょう?

 E-mail
E-mail
 戻る
戻る