Weekend Mathematics乛僐儘僉僂儉幒乛NO.118
| NO.996 | 2001.8.1. | 悈偺棳傟 | 惓幍妏宍乮侾乯 |

奆偝傫偼丄墌偵撪愙偡傞巐妏宍俙俛俠俢偵偮偄偰丄乽僩儗乕儈偺掕棟乿偑偁傞偙偲傪偛懚偠偱偡偐丅
俀慻偺懳曈偺挿偝偺愊偺榓偑俀偮偺懳妏慄偺挿偝偺愊偵摍偟偄偲偄偆傕偺偱偡丅
丂俙俛丒俠俢亄俛俠丒俙俢亖俙俠丒俛俢
偝偰丄栤戣偺惓幍妏宍偱峫偊偰傒傑偡丅傕偪傠傫丄墌偵撪愙偟偰偄傑偡丅
偙偙偱丄偙偺墌偵撪愙偡傞巐妏宍俛俠俢俧傪峫偊傑偡丅
俛俧亖俛俢亖俢俥亖倶丂丂丄丂俠俧亖俢俧亖倷丂丂丄丂丂俙俛亖俛俠亖俠俢亖侾侽偐傜丄
乽僩儗乕儈偺掕棟乿丂俛俠丒俢俧亄俠俢丒俛俧亖俛俢丒俠俧丂偵戙擖偟偰
侾侽丒倷亄侾侽丒倶亖倶丒倷丂丂偙偺椉曈傪侾侽倶倷偱妱傞偲丄
侾乛倶亄侾乛倷亖侾乛侾侽丂偵側傝傑偡丅
亙僐儊儞僩丗偙偺夝朄偼丄乽弶摍悢妛丗2001擭俉寧柧擔梩崋乿偺婰帠偺拞偵丄
娾揷帄峃愭惗偺乽婔壗妛戝帿揟丟戞係姫130崁乿偵彂偄偰偁傞偲丄徯夘偟偰偁傝傑偟偨丅
忋偺婰帠傪撉傫偩偙偲傪晅偗壛偊偰偍偒傑偡丅
側偍丄栤戣採婲偺摨帪惈偵偼戝曄嬃偄偰偄傑偡偗偳丅亜

| NO.997 | 2001.8.1. | yokodon | 墫婎偺愗抐乮俀乯 |
杮栤偱偡偑丄偲傝偁偊偢係庬偺暥帤偺惉偡墌弴楍偵偍偄偰丄摿掕偺暥帤楍傪峔惉偡
傞応崌偺悢偺慻傪峫偊傞偲偄偆曽恓偱峫偊偰傒傑偡丅偑丄偦傟傪慡偰媮傔傞偲側傞偲
丄偦偺慡懱偐傜側傞廤崌偼丄梫慺悢偑偐側傝戝偒偄偱偟傚偆丅
峺慺俙丄俛丄俠丄俢偵傛傝愗抐偝傟傞売強偺悢傪丄偦傟偧傟 a丄b丄c丄d 偲偟傑偡丅
係庬偺墫婎偺憤悢偑 5243 偱丄偦偺慻惉偑俧丄俠丗栺 20% 丄俙丄俿丗栺 30% 偲側
偭偰偄傑偡乮幚偼丄寁嶼偟偰傒傟偽梕堈偵暘偐傞偲偍傝丄偙偆傒側偝側偄偲惉暘墫婎
偺屄悢偑惍悢偵側傜側偄乯丅
偙偙偱偼丄奺乆偺墫婎偺悢傪丄俧丗1048丄俠丗1049丄俙丗1573丄俿丗1573 偲偟偰傒傑偟傚偆丅
慡偰偺墫婎乮幚偼丄惓妋偵偼僰僋儗僆僠僪巆婎偲尵偆傋偒側偺偱偡偑丟屻弎乯偼娐
忬偵暲傫偱偄傞偺偱丄墫婎摨巑偺寢崌偑 5243 儢強桳傞偙偲偵側傝傑偡丅
峺慺俙丄俛丄俠丄俢偺擣幆晹埵偵懚嵼偡傞墫婎偺屄悢傪峫椂偟偰丄奺峺慺偺擣幆晹
埵偑廳暋偟側偄偲偄偆壖掕傪峏偵愝偗傞偲丄係庬椶偺墫婎偵偮偄偰埲壓偺晄摍幃偑惉
傝棫偪傑偡丅
墫婎俙丗a亄3b亄c亝1573
墫婎俧丗a亄2c亄4d亝1048
墫婎俿丗a亄3b亄c亝1573
墫婎俠丗a亄2c亄4d亝1049
偲偙傠偑丄偙傟傪枮偨偡応崌偺悢偺慻偺慡懱偑偮偔傞廤崌偼丄
偐側傝乬戝偒偄乮R4 忋偺偁傞挻捈曽懱偵懏偡傞奿巕揰偺偆偪偺偐側傝偺晹暘傪
愯傔傞偲偄偆堄枴偱乯乭偱偟傚偆丅
廤崌偺奜墑揑婰朄偱彂偔偲側傞偲丄偡偛偄偙偲偵側傝偦偆偱偡丅
偟偐傕丄乽奺峺慺偺擣幆晹埵偑廳暋偟側偄乿偲偄偆壖掕偵傛偭偰丄椺偊偽乬俙俧俠
俿俿俿俙俙俙乭偲偄偭偨攝楍傪峫椂偺懳徾偐傜彍奜偟偰偄傞偺偱丄偦傟傪峏偵峫椂偵
擖傟傞偲側傞偲丄杮栤偱宖偘傜傟偨忦審壓偱偼丄峏偵忬嫷偑暋嶨偵側偭偰偟傑偄傑偡丅
墫婎攝楍偵娭偡傞忣曬偑堦愗柍偄拞偱丄奺峺慺偵傛傞愗抐売強偺屄悢傪昡壙偡傞偲
偄偆偺傕丄栤戣傪夝摎崲擄偵偟偰偄傞傛偆偵姶偠傜傟傑偡丅
偁傞偄偼丄壗偐忋庤偄昡壙曽朄偑偁傞偺偐傕抦傟傑偣傫偑丄杔偼偙傟埲忋偼巚偄偮
偒傑偣傫偱偟偨丅
埲壓丄栤戣偺攚宨偲巚傢傟傞傕偺傪偄偔偮偐曗懌揑偵僐儊儞僩偟偨偄偲巚偄傑偡丅
偙偙偱尵偆係庬椶偺墫婎偲偼丄DNA乮僨僆僉僔儕儃妀巁乯傪峔惉偡傞僰僋儗僆僠僪
偺墫婎晹暘偺偙偲偱偡偹丅
偦傟偧傟丄俙丗傾僨僯儞丄俧丗僌傾僯儞丄俠丗僔僩僔儞丄俿丗僠儈儞丄偱偡丅
娐忬偺 DNA 偼丄堦斒偵偼嵶嬠椶偵懡偔尒傜傟傞傕偺偱丄僾儔僗儈僪偲屇偽傟傑偡丅
偨偩丄婛抦偺僾儔僗儈僪 DNA 偺懡偔偼俀廳嵔偵側偭偰偍傝丄杮栤偱憐掕偟偨侾廳
嵔偵偡傞偵偼丄偁傞暿偺張棟偑昁梫偱偡丅揤慠偱侾廳嵔偺僾儔僗儈僪 DNA 偲偄偆偺
偼丄杔偑抦傝偆傞尷傝丄懡暘懚嵼偟側偄偲巚偄傑偡丅
DNA 傪峔惉偡傞係庬椶偺僰僋儗僆僠僪偺峔惉斾偑丄俙偲俧丄俠偲俿偱傎傏摍偟偔側
偭偰偄傞偺偼丄乮DNA 偺俀廳傜偣傫偺恾傪偛懚偠偺曽側傜棟夝偟傗偡偄偲巚偄傑偡偑
乯偙偺奺乆偺慻偱憡曗揑偵暘巕娫悈慺寢崌傪宍惉偡傞偙偲偱丄DNA 偺崅師峔憿偑宍惉
偝傟偰偄傞偐傜偱偡乮嬊強揑偵俀廳傜偣傫偱側偄峔憿傪偲偭偰偄傞偙偲傕偁傞偺偱丄
昁偢偟傕尩枾偵摍偟偄傢偗偱偼側偄偺偱偡偑乯丅
杮栤偱憐掕偝傟偰偄偨係庬椶偺峺慺偼丄亀惂尷峺慺亁偲屇偽傟傞傕偺偱丄DNA 忋偺
摿掕偺僰僋儗僆僠僪攝楍傪擣幆偟偰偦偺晹埵偺壛悈暘夝斀墳傪怗攠偟傑偡丅DNA 偼係
庬偺僰僋儗僆僠僪乮墫婎亄摐乮僨僆僉僔儕儃乕僗乯亄儕儞巁乯偺堎庬懡検懱偱偁傝丄
摐偺悈巁婎偲儕儞巁偲偱偮偔傜傟傞乽儕儞巁僕僄僗僥儖寢崌乿傪夘偟偰懡検壔偟偰偄
傑偡丅偦偺寢崌傪壛悈暘夝偱愗傞偲偄偆傢偗偱偡丅
惂尷峺慺偺僶僀僆僥僋僲儘僕乕傊偺墳梡椺偼偄偔偮偐桳傝傑偡偑丄椺偊偽埲壓偺傛
偆側椺偑偁傝傑偡丅
戝挵嬠傪巊偭偰丄偁傞儁僾僠僪乮椺偊偽僀儞僔儏儕儞乯傪憹傗偦偆偲偡傞応崌丄惂
尷峺慺傪巊偭偨 DNA 偺愗傝挘傝偼傛偔巊傢傟傑偡丅惂尷峺慺傪梡偄偰丄摿掕偺僾儔
僗儈僪偵栚揑偺儁僾僠僪傪僐乕僪偡傞堚揱巕 DNA 傪嫴傒崬傒丄偦傟傪戝挵嬠偵姶愼
偝偣偰丄戝挵嬠偺嬠懱撪偺戙幱斀墳宯傪巊偭偰栚揑偺抈敀幙傪嶌傜偣傞偲尵偆偙偲偼
丄尰嵼椙偔峴傢傟偰偄傑偡丅偨偩丄姶愼偝偣偨偄恖岺 DNA乮偙傟傪暘巕惗暔妛偺嬈奅
偱偼亀儀僋僞乕亁偲屇傫偱偄傑偡乯傪幚嵺偵偮偔傞偵摉偨偭偰偼丄梋寁側偲偙傠傪愗
傜側偄傛偆偵丄攝楍婛抦偺僾儔僗儈僪偲嶌梡婛抦偺惂尷峺慺傪忋庤偔慻傒崌傢偣偰傗
傞偺偑晛捠偱偡偟丄偦傟偱傕栚揑偺恖岺 DNA 偑摼傜傟傞妱崌乮斀墳廂棪乯偼丄偦傫
側偵崅偔側偄偺偑晛捠偱偡丅
偨偩丄儀僋僞乕惗惉偺斀墳岠棪偺岦忋偺壜擻惈傪棟榑揑偵峫偊傞晍愇偲偟偰丄傾僀
僨傿傾偲偟偰忋庤偔偄偔偐偳偆偐偼偪傚偭偲偳偆偐側丠乮幚嵺偵偼丄斀墳忦審偺岺晇
偱夝寛偝傟傞偙偲偑懡偄偩傠偆乯偲偼巚偄傑偡偑丄拝娽揰偲偟偰偼杮栤偼偪傚偭偲嫽
枴怺偄偲巚偄傑偟偨丅攝楍偵娭偡傞壗傜偐偺忦審偑梌偊傜傟偰偄傟偽丄傕偭偲媍榑偟
傗偡偄栤戣偵側偭偨偲巚偄傑偡丅

| NO.998 | 2001.8.1. | 悈偺棳傟 | 抋惗擔 |
懢榊偝傫偼丄愭擔丄撉幰偺曽偐傜偙傫側搳峞栤戣傪捀偒傑偟偨偺偱丄崱夞偺墳曞栤戣偵偟傑偟偨丅
巹丆傉傝偭傉仐戝妛堾惗偱偡丏
偪傚偭偲柺敀偄栤戣傪峫偊偨偺偱丆傛偐偭偨傜庢傝忋偘偰傕傜偊傞偲偆傟偟偄偱偡丏
栤戣侾丂侾俈恖偄偰丆抋惗擔偑摨偠恖偑彮側偔偲傕侾慻偄傞妋棪偼丠
栤戣俀丂侾俈恖偄偰丆抋惗擔偑摨偠傕偟偔偼侾擔堘偄偺恖偑彮側偔偲傕侾慻偄傞妋棪丠
侾俈偼N恖偱傕峔傢側偄偦偆偱偡偐傜丄捛壛偟傑偡丅
栤戣俁丂俶恖偄偰丆抋惗擔偑摨偠恖偑彮側偔偲傕侾慻偄傞妋棪偼丠
栤戣係丂俶恖偄偰丆抋惗擔偑摨偠傕偟偔偼侾擔堘偄偺恖偑彮側偔偲傕侾慻偄傞妋棪丠

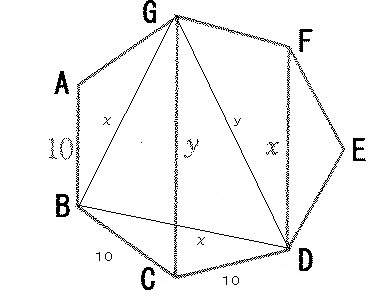
| NO.999 | 2001.8.1. | Junko | 曻暔慄忋偺奿巕揰乮俀乯 |
乮1乯嬋慄俠1丗y 亖(併2)丒x(x-1) 忋偺奿巕揰傪丄慡偰媮傔傛丅
柧傜偐偵丄(侽丆侽)偲(侾丆侽)偲偄偆奿巕揰偑懚嵼偟傑偡丅
偙傟埲奜偵偼懚嵼偟側偄偙偲傪帵偟傑偡丅
戞俁偺奿巕揰(倶0丆倷0)偑懚嵼偟偨偲偡傞偲丄
y0亖(併2)丒x0(x0-1)丄倶0亗侽丆侾
偲偙傠偑丄
y0/x0(x0-1) 亖併2偲側傝丄
偙傟偼桳棟悢亖柍棟悢偲偄偆柕弬傪婲偙偡丅
傛偭偰丄奿巕揰偼俀揰偟偐懚嵼偟側偄丅
乮俀乯a丄b丄c 傪幚悢偲偡傞丅
丂嬋慄俠丗y 亖 ax2+bx+c 忋偵俁屄偺憡堎側傞奿巕揰偑懚嵼偡傞側傜丄偙偺嬋慄俠
忋偵偼柍尷屄偺奿巕揰偑懚嵼偡傞偙偲傪徹柧偣傛丅
嬋慄俠丗y 亖 ax2+bx+c 忋偵俁屄偺憡堎側傞奿巕揰偑懚嵼偡傞側傜丄
a,b,c丂偼丄桳棟悢偲側傝傑偡丅
俁屄偺憡堎側傞奿巕揰傪丄(倶1丆倷1)丄(倶2丆倷2)丄
(倶3丆倷3)偲偟傑偡丅
倷1亖倎倶12亄倐倶1亄們
倷2亖倎倶22亄倐倶2亄們
倷3亖倎倶32亄倐倶3亄們
偙傟傪俁尦侾師曽掱幃偲偟偰a,b,c丂傪夝偒傑偟偨丅
(寁嶼娫堘偄傪偟偰偄側偗傟偽丄偄偄偺偱偡偑丒丒丒)
a亖(倶1倷2亅倶1倷3亅倶2倷1亄倶2倷3亄倶3倷1亅倶3倷2)
乛(倶1亅倶2)(倶2亅倶3)(倶3亅倶1)
b亖(亅倶12倷2亄倶12倷3亄倶22倷1亅倶22倷3亅倶32倷1亄倶32倷2)
乛(倶1亅倶2)(倶2亅倶3)(倶3亅倶1)
c亖(倶12倶3倷2
亅倶12倶2倷3
亅倶22倶3倷1
亄倶22倶1倷3
亄倶32倶2倷1
亅倶32倶1倷2)
乛(倶1亅倶2)(倶2亅倶3)(倶3亅倶1)
偲偄偆傢偗偱丄a,b,c丂偼丄桳棟悢偱偡丅
a=p/q丄b=r/s丄c=t/u丂q,s,u亗0丂偲偍偔偲丄
y 亖 ax2+bx+c丂
丂亖(p/q)x2+(r/s)+(t/u)丂偲側傝丄
倶偵丄q丂偺岞攞悢(柍尷偵偁傞)傪梌偊傟偽丄倷偼惍悢抣偲側傞丅
偮傑傝丄嬋慄俠忋偵偼柍尷屄偺奿巕揰偑懚嵼偡傞丅

| NO.1000 | 2001.8.3. | yokodon | 曻暔慄忋偺奿巕揰乮俁乯 |
乮2乯偵娭偟偰偼丄慜敿偼惓偟偄偱偡偑丄屻敿偑巆擮側偑傜僴僘儗偱偡丅
俁屄偺奿巕揰偑偁傞偙偲偐傜丄a丄b丄c 偑桳棟悢偵側傞偙偲傪帵偡晹暘偼惓偟偄偱
偡丅偟偐偟丄嵍婰偺媡柦戣偵偁偨傞亀a丄b丄c 偑桳棟悢側傜丄嬋慄俠忋偵乮彮側偔偲
傕乯俁屄偺奿巕揰偑懚嵼偡傞亁偲偄偆柦戣偼丄堦斒偵偼惓偟偔偁傝傑偣傫丅
椺偊偽丄y亖x2+1/2丂偑斀椺偱偡丅
惓偟偔偼丄乽a丄b丄c 偑桳棟悢偱偁傞乿偲偄偆忦審偺壓偱丄嬋慄俠忋偺偁傞奿巕揰
乮x1,y1乯偲惍悢値偵懳偟偰丄
俠偺倶偵 x1亄値傪戙擖偟偨応崌偵憡摉偡傞埲壓偺
抣倄偑惍悢偲側傞傛偆側値偑柍尷屄懚嵼偡傞偙偲傪帵偡偙偲偵側傝傑偡
倄亖a(x1亄値)2亄b(x1亄値)亄c
幚嵺丄
倄亖y1亄(2a丒x1亄b)値亄a丒値2
側偺偱丄a亖p/q丄b亖r/s乮p 偲 q丄r 偲 s 偼奺乆屳偄偵慳側惍悢乯偲偍偔偲丄値偑
q 偲 s 偺岞攞悢偱偁傟偽倄偼惍悢偱偡丅
乮2乯偵娭偟偰丄埲壓偺摨抣娭學偑惉傝棫偭偰偄傑偡丅
乽俠忋偵俁屄偺憡堎側傞奿巕揰偑懚嵼偡傞乿
仼仺乽俠忋偵奿巕揰偑懚嵼偟丄a丄b丄c 偑桳棟悢偱偁傞乿
仼仺乽俠忋偵偼柍尷屄偺奿巕揰偑懚嵼偡傞乿
曻暔慄忋偺奿巕揰偵娭偟偰丄屄悢偱暘椶偡傞偲
侽屄丗椺偊偽丄y亖x2亄併2丄y亖x2亄x亄1/2
侾屄丗椺偊偽丄y亖併2丒x2
俀屄丗椺偊偽丄y=併2丒x(x-1)
柍尷丗椺偊偽丄y亖(1/8)x2亄(4/3)x亄1/2
丒丒丒偺傛偆偵側傝傑偡丅
慡偔摨偠峫嶡傪丄俁師嬋慄傗堦斒偺倣師嬋慄乮倣丗帺慠悢乯偵娭偟偰傕峴偆偙偲偑
弌棃傑偡丅
椺偊偽丄俁師嬋慄偺応崌偼丄侽丄侾丄俀丄俁丄柍尷乧偱偡丅
偲偙傠偑丄偪傚偭偲俁師嬋慄偺宍傪偄偠偭偰丄
y2亖x3亄1
側偳偲偟偰偟傑偆偲丄堦嫇偵栤戣偑擄偟偔側偭偰偟傑偄傑偡丅
偙偺応崌偼丄奿巕揰偺屄悢偼俆屄偱偡丅偦偺俆屄傪尒偮偗傞偺偼帋峴嶖岆偱傕壗偲
偐側傝傑偡偑丄偦偺俆屄偵尷傞偙偲傪帵偡偺偼丄偦傟傑偱偺媍榑偲偼慡偔堘偭偰擄偟
偔側偭偰偟傑偄傑偡丅偨偩丄偙傟偑懏偡傞堦孮偺嬋慄乮亀懭墌嬋慄亁偲偄偄傑偡偑乯
偵娭偡傞偁傞桳柤側掕棟偑偛偔嵟嬤徹柧偝傟偨偲偄偆榖偑偁傝傑偟偰丄偦傟偑僼僃儖
儅乕偺嵟廔掕棟偲枾愙側娭楢傪帩偮丄偲偄偆傢偗偱偡乧偲偄偆榖偺嬝傪峫偊偰偄偨偺
偱偡偗傟偳偹乮嬯徫乯丅丂

| NO.1001 | 2001.8.8. | 悈偺棳傟 | 2001乽崅峑悢妛僙儈僫乕乿 |
丂婒晫導偱偁偭偨乽崅峑悢妛僙儈僫乕乿偵嶲壛偟偰丄島巘偺拀攇戝妛搉曈岞晇嫵庼偺島媊傪
暦偄偰偒傑偟偨丅僥乕儅偼
乽僼傽儖儅乕偺掕棟傪夝寛偡傞偵偁偨傞宱堒偲徹柧偺奣梫乿偱偡丅
丂嵟弶偐傜丄庴島惗偵椡偢偔丄乽悢妛傪妛傇偺偵昁梫側偙偲偼丄丄恖傛傝憗偔夝偔曽朄偩偗偱側偔丄
側偤偙偺棟榑偑惗傑傟偨偐傪峫偊傞偙偲偱偡丅帺暘偺巚峫嬻娫傪偄偐偵峀偘傞偐側傫偱偡丅
偙傟偑悢妛偺僟僀僑儈側傫偱偡丅乿
島媊偺拞偵偱偰偒偨婔偮偐偺栤戣傪搳峞偟傑偡丅
栤戣侾丗擏壆偵攦偄暔偵峴偭偰丄併俀倠倗偺媿擏傪攦偭偰偒偰偔偩偝偄丅
丂丂丂丂偁側偨偑擏壆偺庡恖側傜偳偆傛偆偵偟偰丄應傝傑偡偐丅
栤戣俀丏嶰暯曽偺掕棟傪抦偭偨偽偐傝偺拞妛惗偵丄俁曈偺挿偝偑丄
俁們倣丄俆們倣丄俈們倣偺嶰妏宍偑偁傞丅
丂偙偺偲偒丄曈偑俈們倣偱偁傞懳妏偺妏搙偼壗搙偱偡偐丅
栤戣俁丗倎丄倐丄們偑帺慠悢偺偲偒丄師偺嶰暯曽偺掕棟偺夝傪堦斒偵昞偟偰偔偩偝偄丅
乮侾乯倎俀亄倐俀亖們俀
乮俀乯倎俀亄乮倎亄侾乯俀亖們俀
乮俁乯倎俀亄倐俀亖乮倐亄侾乯俀
乮係乯倎俀亄倐俀亖乮俀倎亇侾乯俀
栤戣係丗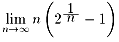 偺抣偱偡丅乮庴島惗偵偼丄寢壥偲偟偰巊偄傑偟偨乯
偺抣偱偡丅乮庴島惗偵偼丄寢壥偲偟偰巊偄傑偟偨乯
偝傜偵丄偙偺抣傪揹戩偱媮傔傑偟偨丅偙偺曽朄傕峫偊偰偔偩偝偄丅偨偩丄値亖侾侽偱廫暘偱偡丅
嵟屻偵偼丄僼儔僀嬋慄偐傜丄僼儔僀梊憐丄巙懞亖扟嶳梊憐偺榖偱偱偰偒偰島媊偑廔椆偟傑偟偨丅

| NO.1002 | 2001.8.10. | 俛倧倱倱俥 | 抋惗擔乮俀乯 |
抋惗擔偵娭偟偰偼
摿堎擔乮12/31丄1/1丄2/29丄3/31丄4/1乯偺栤戣偑偁傞偦偆偱偡偑丄悢妛揑偵偼偦傟
傪柍帇偟偰偲丒丒
俶恖偄偰丆抋惗擔偑摨偠恖偑彮側偔偲傕侾慻偄傞妋棪偼
1-366PN/366N偱偡偐傜丄
1-(365/366)(364/366)丒丒丒乷(366-N+1)/366乸丂乧嘆丂乧栤偄俁偺夝
嘆偱俶=17偵偟偰
17恖偄偰丆抋惗擔偑摨偠恖偑彮側偔偲傕侾慻偄傞妋棪偼
1-(365/366)(364/366)丒丒丒(350/366)佮0.999994乧丂丂乧栤偄1偺夝

| NO.1003 | 2001.8.14. | yokodon | 10偱妱偭偨梋傝乮侾乯 |
柾帋僔儕乕僘2
丂帺慠悢 n 傪 10 偱妱偭偨梋傝傪 L(n) 偲偡傞丅
乮1乯帺慠悢 m丄n 偵懳偟偰丄L(m)亖L(n)亖1 偺偲偒丄L(mn) 偺抣傪媮傔傛丅
乮2乯n 傪係偺攞悢偲偡傞丅L(3n) 媦傃 L(3^(3n)) 偺抣傪媮傔傛丅

| NO.1004 | 2001.8.14. | 昹揷丂柧枻 | 峆摍幃偺夝偒曽 |
師偺峆摍幃偺栤戣傪丆惗搆偵壗婥側偔弌戣偟偨偺偱偡偑丆柺搢側偙偲偵側偭偰偟傑偄傑偟偨丏
栤戣偼師偺捠傝偱偡丏
乽俀倶2亄倎倶倷亅俁倷2亄倶亄係倷亅侾亖(俀倶亄倷亄倐)(倶亅俁倷亄們)偑倶丆倷偺峆摍幃偵側傞傛偆偵丆掕悢倎丆倐丆們偺抣傪掕傔傛丏乿
峆摍幃偺夝偒曽偵偼丆學悢斾妑丆悢抣戙擖偺俀捠傝偺曽朄偑偁傝丆
働乕僗僶僀働乕僗偱寁嶼偑妝偵側傞曽傪慖傇偲傛偄丆偲巜摫偟偰偄傑偡丏
偨偩偟丆悢抣戙擖朄偺応崌丆昁梫廫暘偺娭學傪枮偨偡堊偵丆
嵟屻偵乽媡偵偙偺偲偒丆嵟弶偺摍幃傪枮偨偡丏乿偲偄偆暥嬪傪晅偗壛偊側偔偰偼側傝傑偣傫丏
戙擖偟偨抣偺偲偒偵惉棫偡傞偙偲偼暘偐傞偺偱偡偑丆
懠偺偡傋偰偺応崌偵傕惉棫偡傞偙偲傪尵傢側偔偰偼側傜側偄偺偱偡丏
幚幙揑偵偼丆壗傕峫偊偢偵偙偺暥嬪傪婡夿揑偵彂偒壛偊傞偺偑捠忢偱偡丏
惉棫偡傞偺偑暘偐傝愗偭偰偄傞丆崱傑偱偦偆偩偭偨偐傜丆偲偄偆偺偑丆杮壒偱偡丏
偟偐偟丆忋婰偺栤戣偺応崌丆悢抣戙擖朄偱傗偭偰傒傞偲丆偙偺峫偊曽偑偔偢傟偰偟傑偆偺偱偡丏
夝偄偰傒傑偡丏
俀倶2亄倎倶倷亅俁倷2亄倶亄係倷亅侾亖(俀倶亄倷亄倐)(倶亅俁倷亄們)乧乧乧嘆
偲偡傞丏
丂嘆偵倶亖侽丆倷亖侽傪戙擖偡傞偲丆亅侾亖倐們乧乧乧嘇
丂嘆偵倶亖侽丆倷亖侾傪戙擖偡傞偲丆侽亖(侾亄倐)(亅俁亄們)乧乧乧嘊
丂嘆偵倶亖侾丆倷亖侾傪戙擖偡傞偲丆倎亄俁亖(俁亄倐)(亅俀亄們)乧乧乧嘋
丂嘊偐傜丆倐亖亅侾傑偨偼們亖俁
i).倐亖亅侾偺偲偒丆嘇偐傜丆們亖侾
丂丂嘋偵戙擖偡傞偲丆倎亄俁亖亅俀丂丂丂亪倎亖亅俆
丂丂偙偺偲偒丆嘆偼
丂丂丂俀倶2亅俆倶倷亅俁倷2亄倶亄係倷亅侾亖(俀倶亄倷亅侾)(倶亅俁倷亄侾)
丂偲側傝丆忢偵惉棫偡傞丏
ii).們亖俁偺偲偒丆嘇偐傜丆倐亖亅侾乛俁
丂丂嘋偵戙擖偡傞偲丆倎亄俁亖俁亅侾乛俁丂丂丂亪倎亖亅侾乛俁
丂丂偙偺偲偒丆嘆偼
丂丂丂俀倶2亅倶倷乛俁亅俁倷2亄倶亄係倷亅侾亖(俀倶亄倷亅侾乛俁)(倶亅俁倷亄俁)
丂丂亖俀倶2亅俆倶倷亅俁倷2亄侾俈倶乛俁亄係倷亅侾
丂偲側傝丆偙傟偼倶丆倷偺峆摍幃偱偼側偄丏
i).丆ii).偐傜丆摎偼倎亖亅俆丆倐亖亅侾丆們亖侾偱偁傞丏
傗偼傝丆栤戣偼僐僣僐僣偲挌擩偵夝偄偰偄偐側偔偰偼側傜側偄偺偱偟傚偆偐丏
峆摍幃偵偼學悢斾妑朄偑堦斣傛偄偺偱偟傚偆偐丏

| NO.1005 | 2001.8.14. | 搉晹丂彑 | 惓曽宍偺愜傝巻乮俀乯 |
悢妛偺廳梫惈
丂悢妛傪妛傇偲尵偆帠偼丄傕偼傗岞棟丄掕棟傗岞幃傪巊偭偰徹柧偡傞帠丄
寁嶼偡傞帠偱偼柍偔側偭偰偄傞偲巚偆丅
丂悢妛傪妛傇偲尵偆帠偼丄怴偟偄掕棟傗岞幃傪敪尒偡傞帠偱偁傝丄栤戣
傪夝寛偡傞擻椡傪奐敪偡傞帠丄妶惈壔偡傞帠偱偁傞偲尵偭偰椙偄偺偱偼
側偄偐丅偦傟備偊偵丄惌帯傗宱嵪偺暘栰偵偍偄偰傕偦偺悢妛偑廳梫偲側傞偺偱偡丅
丂乽憂憿椡乿偲尵偆尵梩偼偛偔堦斒揑偱偡偑丄乽岺晇椡乿偲偼偁傑傝尵
傢側偄傛偆偱偡丅丂乽憂憿椡乿偲偼丄傂傜傔偒椡偺帠偱偁傝丄乽岺晇椡乿
偲偼丄偦偺傂傜傔偄偨暔丄傂傜傔偄偨帠傪嬶懱壔丄嬶尰壔偡傞僾儘僙僗
偵偍偗傞栤戣夝寛椡偲尵偭偰椙偄丅
丂婇嬈幮夛偵偍偗傞丄憂憿椡偲岺晇椡偲偼丄偡側傢偪乽儓僔両丂侾侽侽墌偱
嶌傠偆乿偲尵偆憂憿椡偲乽偳偺傛偆偵偟偰偦傟傪嶌傞偺偐乿偲尵偆岺晇椡
偺娭學偱偁傞丅
丂懘張偱偙偺乽岺晇椡乿傪奐敪偡傞偲尵偆帠丄偦傟偼椺偊偽丄堦枃偺挿曽宍
偺梡巻傪惗搆偵梌偊丄乽偦偺梡巻偺柺愊傪嶰摍暘偣傛乿偲偡傞帪丄偳偺傛偆
偵偙偺栤戣傪夝寛偡傞偺偐偲尵偆擻椡傪奐敪偡傞偵摍偟偔丄偙傟偼戝曄
廳梫側帠偱偁傞丅夝摎偼堦捠傝偱偼偁傝傑偣傫丅
丂妛惗偨偪丄偄傗丄懡偔偺幮夛恖偑悢妛寵偄偱偁傞尰忬偼懡偄偵桱椂偝傟
側偗傟偽側傜側偄丅巹偼乽岺晇椡乿偺奐敪丄妶惈壔偺偨傔偵丄採埬傪懕偗
偰偄偒偨偄偲巚偄傑偡丅
栤戣
乽梡巻丂A4斉偺柺愊偺侾/3偲側傞惓曽宍傪嶌傝側偝偄乿
偙偺梡巻傪巊偄傑偡丅

 E-mail
E-mail
 栠傞
栠傞