
Weekend Mathematics/コロキウム室/NO.115
| NO.973 | 2001.6.2. | 水の流れ | √nに近い整数(1) |
太郎さんは、√n(整数nの正の平方根)にもっとも近い整数をanと表して、
数列{an}を作りました。
実際に、数列を作ってみると、こんな問題ができます。
問題1:an=kとなるnの値の範囲をkで表せ。
問題2:an=kとなるnの個数をkで表せ。
問題3:初項から第2001項までの逆数の和Sを求めよ。
すなわち、S=1/a1+1/a2+1/a3+・・・+1/a2001

| NO.974 | 2001.6.2. | DDT | 蒸気機関車の問題・その後 |
53.蒸気機関車の問題でJunkoさん曰く
「場合によっては1周が100度でもよかったのかもしれない。
(ちょっと不便な気もしますが・・・) 10進法が主流なのに、
なぜ角度のはかり方は違うのでしょう?」
こんな噂があります
最初に申し上げます。史実にもとづかない与太話です。
18〜19世紀にかけてイギリスは七つの海を制覇し、大英帝国に日の沈む所なしと言われました。 そのきっかけとなったのは、スペインのアルマダ(無敵艦隊)をドーバー海峡で撃破した、 ネルソン提督率いるイギリス艦隊です。
当時スペインのフェリペ4世は、角度の単位としてgrad(1直角100°)を制定していました。 一方イギリスは、今も昔もdegree(1直角90°)です。 で、砲撃による海戦がどうなったかというと・・・。
イギリス艦隊:
「右舷前方30°に敵艦発見!。撃て〜!!」とネルソン提督。
「それ〜っ!、いてまえ〜〜!!」と砲撃手。
ドカン!ドカン!!ドカン!!!(大砲の音)
スペイン艦隊:
「右舷前方30.3333333333333333333333333333333333333333333333・・・」と息切れ。
「はやく撃てって言ってくれ〜〜!」と砲撃手。
ドカン!ドカン!!ドカン!!!(大砲を食らった音)
こうしてスペイン艦隊は、ただの1発も撃ち返すことなく敗北を迎えたそうです。
以上、かなり昔の数学セミナーに出ていたと思われるお話です。
でも右舷前方30°でなく、違う角度だったら、立場が逆になったのでは?
そこでやってみました。1直角/2,1直角/2,1直角/3,1直角/4・・・と調べて行くと・・・。
| [gradの場合] | [degreeの場合] |
|---|---|
| 100/2=50 | 90/2=45 |
| 100/3=33.333333333333・・・ | 90/3=30 |
| 100/4=25 | 90/4=22.5 |
| 100/5=20 | 90/5=18 |
| 100/6=16.666666666666・・・ | 90/6=15 |
| 100/7=14.2857142857・・・ | 90/7=12.857142857142・・・ |
| 100/8=12.5 | 90/8=11.25 |
| 100/9=11.111111111111・・・90/9=10 | |
| 100/10=10 | 90/10=9 |
| ・ | |
| 100/12=8.3333333333・・・ | 90/12=7.5 |
| ・ | |
| 100/15=6.6666666666・・・ | 90/15=6 |
| 100/16=6.25 | 90/16=5.625 |
| ・ | |
| 100/18=5.5555555555・・・ | 90/18=5 |
| ・ | |
| 100/20=5 | 90/20=4.5 |
| ・ | |
| 100/24=4.1666666666・・・ | 90/24=3.75 |
| 100/25=4 | 90/25=3.6 |
| ・ | |
| 100/30=3.3333333333・・・ | 90/30=3 |
| ・ | |
| 100/32=3.125 | 90/32=2.8125 |
| ・ | |
| 100/36=2.7777777777・・・ | 90/36=2.5 |
| ・ | |
| 100/40=2.5 | 90/40=2.25 |
| ・ | |
| 100/45=2.2222222222・・・ | 90/45=2 |
| ・ |
製図の得意な友人に、30°をフリーハンドで書いてもらったことがあります。
その精度は、30.00011°というとんでもないものでした。
例えば30°とかいう角度はもう、私達の体に叩き込まれてる気がします。

| NO.975 | 2001.6.15. | DDT | √nに近い整数(2) |
n≧1と考え、「√n(整数nの正の平方根)にもっとも近い整数an」
の意味を四捨五入とします。
問題1:an=kとなるnの値の範囲をkで表せ。
√nの四捨五入がkと考えると、
k−0.5≦√n<k+0.5
です。いまn≧1としているので、k≧1より、k−0.5≧1−0.5≧0.5>0で、
(k−0.5)2≦n<(k+0.5)2
k2−k+0.25≦n<k2+k+0.25 (1)
となります。k2−kとk2+kは明らかに整数なので、
(1)の範囲にある整数は、k2−k+0.25の上隣りの整数
k2−k+1から、k2+k+0.25の下隣りの整数k2+kまでとなりますが、
心配なのは、k2+k<k2−k+1の場合です。
k2+k<k2−k+1からkの範囲を定めると、
k2+k<k2−k+1
2k<1
k<1/2<1
となり、k≧1ではokでした。従って、an=kとなるnの値の範囲は、
k2−k+1<n<k2+k
です。
問題2:an=kとなるnの個数をkで表せ。
問題1より、k2−k+1≦n≦k2+kなので、
k2−k+1からk2+kまでの幅が2k−1で、端の1個分を足し、2k個。
問題3:初項から第2001項までの逆数の和Sを求めよ。
すなわち、S=1/a1+1/a2+1/a3+・・・+1/a2001
Ak={an|an=k}とします。
a2001が含まれるAkを探します。問題1より
k2−k+1≦2001≦k2+k
であれば良い。
k2−k−2000≦0 (2)
かつ
k2+k−2001≧0 (3)
となるから、(2)でα2−α−2000=0とおいて、
α=(1±(1+4・2000)1/2)/2=(1±80011/2)/2≒45.2,−44.2
(3)でβ2+β−2001=0とおいて、
β=(−1±(1+4・2001)1/2)/2=(−1±80051/2)/2≒44.2,−45.2
従って、44.2≦k≦5.2からk=45。
k=45のときk2−k+1=1981なので、
a2001はA45の2001−1981+1=21番目の
anになる。
問題2より、各Akには2k個のanが含まれ、それらの値はみなkだから、


| NO.976 | 2001.6.16. | 水の流れ | ウェアリングの予想(1) |
太郎さんは、以前「数秘眺望発見」の中で、フェルマーがギリシァ人数学者のディオファンタスが書いた本の複写の余白に
「全ての自然数は、どれも1,3,6,10,15,21、・・・という三角数であるか、 あるいは2個または3個の三角数の和で表される」と記したとある。また、「全ての自然数はm個以下のm角数で表される」と彼は考えた。
「全ての自然数は、多くても4個の平方数の和、9個の立方数の和、・・・として表れる」
これは、フェルマーの予想の四角数(=平方数)の場合と一致するので、
ラグランジュによって証明済みです。
ここで、立方数についての問題です。コンピュータさんにお願いします。
問題1.最高の9個の立方数の和で表される自然数を教えてください。
問題2.8個の立方数の和で表される自然数を教えてください。
問題3.7個の立方数の和で表される自然数を教えてください。
さらに、ウェアリングの予想は、平方数や立方数でない4乗数の和にも及んでいる。
当然、5乗数の和、6乗数の和、・・・有限個の和で全ての自然数を表せると予想している。
<参考文献:図解雑学 数の不思議 今野紀雄著 ナツメ社 >

| NO.977 | 2001.6.21. | Kernighan | ウェアリングの予想(2) |
任意のk>0に対して、どんな正の整数も高々有限個のk乗数の和でかける。
はヒルベルトが証明しています。
これに関連して、
全ての整数NはN=a2+b2-c3(a,b,cは整数)とかける。
[Elkies and Kaplansky] Problem10426.Am.Math.Monthly,102:70,1995
が証明できます。

| NO.978 | 2001.6.24. | Junko | GRAPES |
「GRAPES」というソフトをご存知でしょうか?
大阪教育大学附属高等学校池田校舎の友田勝久先生がお作りになったフリーソフトウェアで、
陽関数、陰関数、媒介変数のグラフなど、簡単な操作で描いてくれます。パラメータの増減や、点の
ドラッグによってグラフを動かし、残像機能によって描いたグラフを残すこともできます。
授業で利用できるかなあと思って、使ってみたのですが、まず自分がはまってしまいます。おもしろいです。
ダウンロード、及び詳しい内容は、GRAPESへ。
HTMLマニュアル、サンプルデータもそろっています。
また文英堂から、「GRAPES パーフェクトガイド」が出版されています。(\1800)
いろいろな機能がオールカラーで丁寧に説明されています。
本体、サンプルデータの入ったCD-ROM付きで、是非おすすめです。

| NO.979 | 2001.6.28. | DDT | 微分(1) |
微分 その1(接線が住んでいる?)
かなり以前に、「微積分の意味(日本評論社,森毅)」と
「ベクトル解析(国土社,森毅)」を読んでいたとき、
微分とは関数の線形化操作そのもののことだと思いました。
つまり微分とは、微分係数を求めることでも導関数を求めることでもなく、
f(x+dx)=f(x)+f'(x)dx
という微分の形をつくることなのだと。
今この2冊を読み返してみても、なぜその時そう思ったのか見当もつきません。
確かに一次化とか線形化とか、それらしきことは書いてありますが、
微分が線形化操作そのものだとは一言も書いてありません。
だからこれは私の誤解かもしれませんが、恐らく「ベクトル解析」の序文で、
関数を微分して線形化して線形代数に載っけて料理するのが、微分の現代風の扱い、
という一文に引っ掛かったのだと思います。
そこで「じゃあ、関数の一点には一次関数が住んでるのか?」と思い立ちました。
もしこれが本当なら、平均速度の極限として定義される瞬間速度についてわまる、
瞬間には、動いてないのに速度あり、という異常事態を避けて通れるのでは、という次第です。
異様と感じるのは、個人的感覚なんですが・・・。
関数の一点に一次関数が住んでるのかどうかを見るためには、1点の内部を覗けばよろしい。
どうやって?・・・恥ずかしながら、考えつけたのは以下のようなものでした。
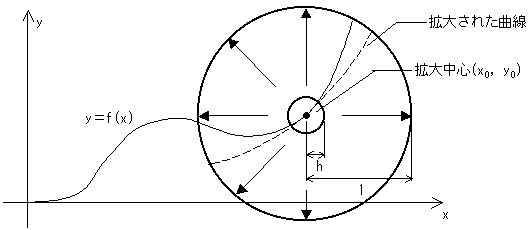
|h|<1として、上図の半径hの円内に含まれる関数y=f(x)の部分を1/h倍に拡大する。
半径hの円はいわば顕微鏡の対物レンズで、半径1の円は1/h倍に拡大された対物レンズの像を写す
接眼レンズです。ここで、h→0の極限をとれば、対物レンズは拡大中心(x0,y0)
に収束するので、h→0のときに接眼レンズに写った像は、
1点の内部での関数の姿ではなかろうか?・・・考えつけるのは、この辺は限界でした。
実行します。
関数y=f(x)をy=f(x)上の1点(x0,y0)のまわりで等方的に拡大するために、
(x0,y0)が原点に来るようにy=f(x)を平行移動します。
y+y0=f(x+x0) (1)
(1)を原点まわりに1/h倍に等方的に拡大します。
h・y+y0=f(h・x+x0) (2)
左辺のhとy0を移項します。
y=(f(x・h+x0)−y0)/h (3)
h→0の極限をとります。
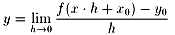 (4)
(4)
y0=f(x0)でなので、
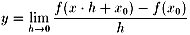 (5)
(5)
となります。(5)で合成関数の微分公式を思い出すと、
y=f'(x0)・x (6)
です。(6)を(x0,y0)を通るように、もとの位置に戻します。
y−y0=f'(x0)(x−x0) (7)
これは接線の方程式だ!
考えれば当たり前なのですが、この結果を見たときは、非常に驚きました。
そういうわけで、関数の1点の内部には接線が住んでいると考えて良いのだと、
安心して思うようになりました。だから瞬間には動いていなくても、
一次関数が関数の1点に住んでる以上、瞬間速度は想定して良いのだ。
それは平均速度の理想化にすぎないのだから。考えてみれば当たり前の結果でした。
関数の1点の内部に接線が住んでるとは、常識的にいえば、いたるところ微分可能な
関数は折れ線近似の極限として得られる、といったところだと思います。ここまで考えたときに、
ふと頭をよぎったものがありました。それはテーラー級数です。
というわけで厚かましくも、「微分 その2」を書く気でいます。

 E-mail
E-mail
 戻る
戻る