Weekend Mathematics乛僐儘僉僂儉幒乛1997乛NO.1
NO.1丂丂丂6/1丂丂丂MK142857
悢妛偵嫽枴偑偁傞愮梩巗嵼廧偺崅峑侾擭惗偱偡丅
僀儞僞乕僱僢僩忋偱愭惗偺儂乕儉儁乕僕傪尒偰嫽枴傪帩偪傑偟偨丅
嫽枴偁傞栤戣傪偍憲傝偟傑偡丅傕偟傛偐偭偨傜愭惗偺弌戣椺偵壛偊偰壓偝偄丅
傑偨丄杔偺栤戣椺偵僐儊儞僩偑偁傝傑偟偨傜丄
偍朲偟偄偱偟傚偆偑曉怣傪壓偝偄丅
栤戣侾
48134813,53775377側偳偺傛偆偵摨偠係寘偺帺慠悢傪俀偮暲傋偨宍偺俉寘偺帺慠悢偺拞偱丄
17447偱妱傝愗傟傞嵟戝偺帺慠悢傪媮傔偰壓偝偄丅
乮弌揟丂嶼悢侾侽侽偺擄栤丄婏栤俹俀侾偺椶戣丂侾俋俋俁擭島択幮乯
栤戣俀
懢榊孨偼丄庤偵300枃偺僇乕僪傪廳偹偰帩偭偰偄傑偡丅
崱偐傜師偺憖嶌傪偟傑偡丅
傑偢丄堦斣忋偺僇乕僪傪婘偺忋偵抲偒傑偡丅
偦偟偰丄師偺僇乕僪傪帩偭偰偄傞僇乕僪偺堦斣壓偵擖傟傑偡丅
摨偠傛偆偵丄師偺僇乕僪傪婘偺忋偵抲偒丄
偦偺師偺僇乕僪傪帩偭偰偄傞僇乕僪偺堦斣壓偵擖傟傑偡丅
偙偺憖嶌傪偢偭偲孞傝曉偡偲偒丄
懢榊孨偺庤偵嵟屻傑偱巆傞僇乕僪偼丄
弶傔偵帩偭偰偄偨僇乕僪偺拞偺忋偐傜壗斣栚偺僇乕僪偐摎偊偰壓偝偄丅
乮弌揟丂嶼悢僆儕儞僺僢僋戞俀夞戝夛栤戣俇偺椶戣乯
NO.2丂丂6/2丂丂Junko
巹偺夞摎傪偐偒傑偡丅
栤戣侾
戣堄偵偁傞俉寘偺悢偼壓係寘偺晹暘傪a偲偡傞偲丄a亊10001偲偐偗傞丅
偲偙傠偱丄17447=73亊239偲場悢暘夝偱偒傞丅
偙偺73偑10001傪傄偭偨傝妱傞偲偙傠偑儈僜両
10001亊a/17447=10001亊a/(73亊239)=137亊a/239偲側傝丄
偙傟偑妱傝愗傟傞偨傔偵偼丄137偲239偑屳偄偵慺偱偁傞偙偲偐傜丄
a偑239偺攞悢偱偁傟偽傛偄丅
a偼係寘偺帺慠悢偱239偺嵟戝偺攞悢偱偁傟偽傛偄偺偩偐傜丄9799丅
廬偭偰摎偊丄97999799丅偳偆偱偟傚偆丠
偙偺栤戣偱乽17447乿偲偄偆悢帤偼昁慠惈偺偁傞悢帤偱偡丅
栤戣偺弌戣幰偼10001傪73偑妱傝愗傞偲偄偆惈幙傪巊偄偨偄傢偗偱偡偐傜丄
傑偢73偺攞悢偱偁傞昁梫偑偁傝傑偡丅
偦偟偰丄10001/73=137偲17447/73=239偑屳偄偵慺偱側偗傟偽側傝傑偣傫丅
傑偨丄17447偼俆寘埲忋乮偱側偄偲栤戣偑偍傕偟傠偔側偄乯偱側偍偐偮丄
17447/73偼係寘偺彫偝偄曽偐偱偒傟偽俁寘埲壓丅
偙傟傜傪峫偊傞偲丄17447偩偗偱偼側偄偲巚偄傑偡偑偐側傝尷傜傟偰偔傞偟丄
傕偪傠傫壗偱傕偄偄傢偗偱偼偁傝傑偣傫丅
偦偆偄偆堄枴偱昁慠惈偺偁傞悢帤偩偲偄偆傢偗偱偡丅
弌戣幰偺棫応偵偨偭偰峫偊偰傒傞偲傑偨堘偭偨尒曽偑偱偒偰偍傕偟傠偄偲巚偄傑偡丅
師偵栤戣俀偵偮偄偰偱偡丅
奺僇亅僪偵侾偐傜俁侽侽傑偱偺斣崋偑崀偭偰偁傞偲偟傑偟傚偆丅
偙傟偲帡偨傛偆側栤戣偑擔杮悢妛僆儕儞僺僢僋梊慖偺栤戣偵弌戣偝傟偰偄傑偡丅
乽侾偐傜値傑偱偺惍悢偑暲傫偱偄傞偲偒丄
俀偐傜徚偟弶傔偰傂偲偮枅偵悢帤傪徚偟偰備偒丄
抂偵偮偄偨傜愜傝曉偟偰丄媡岦偒偵巆偭偰偄傞悢帤傪傂偲偮枅偵徚偡丅
偦偟偰抂偵偮偄偨傜愜傝曉偟丄埲壓摨條側偙偲傪孞傝曉偡丅
偦偟偰嵟屻偵侾偮偩偗巆傞悢偑壗偱偁傞偐傪峫偊傛偆丅
椺偊偽値亖俆側傜俀丆係丆俁丆俆偲弴偵悢帤偑徚偊嵟屻偵侾偑巆傞丅
傑偨丄椺偊偽値亖俈側傜徚偊傞悢帤偼弴偵俀丆係丆俇丆俆丆侾丆俈偱
嵟屻偵巆傞偺偼俁偱偁傞丅偝偰値亖侾俋俋俈偺偲偒嵟屻偵巆傞悢偼壗偐乿
挧愴偟偰傒偰偔偩偝偄丅
NO.3丂丂丂丂6/7丂丂偪傖傫偨
崱夞偺栤戣乮侾乯偼丄廃傝偵夝偐偣偰尒偨偲偙傠丄戝曄岲昡偱偟偨丅
偲傝偁偊偢棟岺宯偲偄偆偙偲傕偁傝丄侾侽暘傎偳偱傒傫側惓夝偵偨偳傝偮偒傑偟
偨偑丄嵟弶栤戣傪尒偨偲偒偼丄柺怘傜偭偰傑偟偨丅
(^_^;;丂側傫偩偐廳敔偺嬿傪偮偮偔傛偆側栤戣偱偡偑丄偍傕偟傠偐偭偨偱偡丅(^_^)
NO.4丂丂丂丂6/10丂丂丂丂BRAINMANIA
傕偆彮偟儂乕儉儁乕僕傪朙偐偵偟偨偄偺偲丄
巹屄恖偺媈栤傪偐偹偰偍偨偢偹偟偨偄偙偲偑偁傝傑偡丅
侾偮偼乽悢妛偺岠壥乿丅
壗屘偵悢妛傪廗偭偰備偔偺偐丅
尰嵼偺幮夛偺悢妛偺棫応側偳丄
巚偭偰偄傞偙偲傪嫵偊偰梸偟偄偺偱偡偑乧丅
巹側傝偵偼丄悢妛揑峫嶡椡傪抌偊傞傕偺偩偲偐側傝敊慠揑偱偡偑峫偊偰偍傝傑偡丅
傕偆侾偮偑乽摢偑傛偄偙偲偼偳偆偄偆偙偲偐乿丅
崱庤扵傝偱怓乆挷傋偰偄傑偡丅
巹偲偟偰偼丄摢偺椙偝偼戝偒偔暘偗偰俁偮偁傞偲峫偊傜傟傑偡丅
偦傟偼乽婰壇椡乿偲乽棟夝椡乿偲乽敪憐椡乿偲暘偗偰偄傑偡丅
懠偺恖偼偳偆偄偆峫偊曽側偺偐惀旕偲傕抦傝偨偄偲巚偄丄
儊乕儖傪憲傝傑偡丅
壣偑偁偭偨傜儊乕儖壓偝偄丅偱偼丅
NO.5丂丂丂丂6/11丂丂丂MK142857
栤戣3(僆儕僕僫儖)
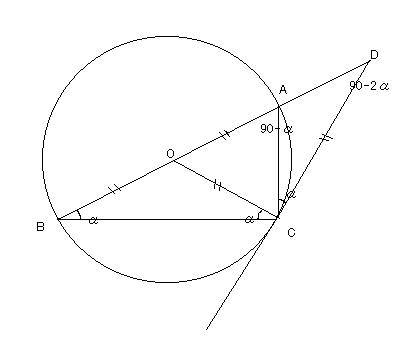
AB傪幬曈偲偡傞捈妏嶰妏宍ABC乮佢B亙45搙乯傪彂偒傑偡丅
捈慄BA偺墑挿忋偵俢傪偲傝丄
佢ABC=佢ACD偲側傞傛偆偵偟偨偲偙傠丄
AB:CD=2:1丂偲側傝傑偟偨丅
佢BAC偺戝偒偝傪媮傔偰壓偝偄丅
栤戣俀
杔偺夝摎椺
傑偢丄帩偭偰偄傞僇乕僪偺枃悢偑2n乮n偼帺慠悢乯偲偐偗傞偲偒丄
嵟屻傑偱庤尦偵巆傞僇乕僪偼丄堦斣壓偺僇乕僪偱偁傞丅--------乮仏乯
傪徹柧偟傑偡丅
NO.6丂丂6/14丂丂Junko
偙傫偵偪偼丅栤戣俀偵偮偄偰偺帣搰偝傫偺夝摎偼偡偽傜偟偄偱偡偹丅
姶摦傕傫偱偡丅
巹偺傛偆偵偁偔偣偔傗傞偺偼摎偊偵偨偳傝偮偄偨偲偟偰傕
偁傑傝旤偟偔偼側偄偱偡傕偺偹丅扙朮偱偡丅
偝偰丄僆儕僕僫儖栤戣偺曽偱偡偗傟偳傕丄偙傟傕棫攈両
曄側尵偄曽偐傕偟傟側偄偗傟偳偪傖傫偲栤戣偵側偭偰偄傑偡丅
摿偵婔壗偺栤戣傪嶌傞偺偼傓偢偐偟偄偲巚偄傑偡丅
忦審傪愝掕偟曄悢傪摦偐偟偨偲偒偵丄
偙偆偄偆忬嫷傪嶌傝弌偟偨偄偲偄偆晽偵栤戣傪嶌偭偰偄偔傢偗偱偡偑丄
忦審傪夁晄懌側偔偦傠偊傞偙偲側偳戝曄側柺偑偁傝傑偡丅
偄傠偄傠側堄枴偱傛偔偱偒偰偄傞偲巚偄傑偡丅夞摎椺傪俀偮偐偒傑偡丅
侾丏

俀丏嶰妏娭悢偺抦幆傪巊偄傑偡丅
侾偺夝朄偼拞妛峑掱搙偺抦幆偱夝偗傑偡傛偹丅
偱傕俀丗侾乮傑偨偼俽俻俼乮俁乯丗侾傑偨偼侾丗俽俼俻乮俁乯側偳乯
偲偄偆摿庩側応崌偱偟偐夝偗傑偣傫丅
俀偺夝朄偼嶰妏娭悢偵娭偡傞抦幆偑昁梫偱偡偑丄
堦斒揑側斾棪偱傕丄
乮嶰妏娭悢昞傗寁嶼婡偵傛傞嬤帡偱偡偑丄乯媮傔傞偙偲偑偱偒傑偡丅
嶰妏娭悢偺墳梡偲偟偰傕偄偄栤戣偩偲巚偄傑偡丅
傑偨丄栤戣偑嶌傟偨傜尒偣偰偔偩偝偄丅
NO.7丂丂6/17丂丂丂Junko 丂丂 NO.4偺敪尵傪庴偗偰
傓偢偐偟偄幙栤傪搳偘偐偗傜傟偰偟傑偭偨偺偱丄
偄傠偄傠偲巚偄弰傜偣偰偼偄偨偺偱偡偑丄
側偐側偐儁儞傪偲傟偢乮僉亅儃亅僪傪偨偨偗偢乯偵崱偵帄偭偰偄傑偡丅
偳偪傜偵偟偰傕戝偟偨偙偲偼偐偗傑偣傫偑丄巹偺巚偆偲偙傠傪偐偄偰傒傑偡丅
悢妛偵偮偄偰丄悢妛傪傗傞恖偼悢妛帺懱偑幮夛偵偳偆峷專偡傞偐偲偐丄
壗偺偨傔偵曌嫮偡傞偐側偳偲偼峫偊偰偄側偄偲巚偄傑偡丅
枹抦偺傕偺偵庝偐傟傞丄恀棟扵媶偺惛恄偩偲巚偄傑偡丅
巹偼戝妛帪戙丄偁傑傝傑偠傔側戝妛惗偱偼側偐偭偨偱偡偗傟偳丄
偱傕悢妛傪妛傇偙偲偼偦傟帺懱偱偲偰傕偍傕偟傠偐偭偨偱偡丅
悢妛偵偼乽旤乿傪姶偠傞偟丄姶摦傕偟傑偡丅
悢妛壢偲偄偆偺偼戝掞偺戝妛偱偼棟壢宯偵埵抲偟傑偡偑丄
懠偺棟壢宯偺妛壢偲偼悘暘堘偆偲巚偄傑偡丅
乮傾儊儕僇偩偭偨偐側丠暥壔宯偺揘妛壢偺墶偵悢妛壢側傫偰戝妛傕偁傞傛偆偱偡丅乯
悢妛偼棟榑傪峔抸偟偰偄偔妛栤偩偲巚偄傑偡丅
偦傟傪昞婰偡傞偺偵悢幃傪梡偄偰偄傑偡丅
帺慠壢妛偺暘栰偼丄傑偢丄帺慠尰徾偁傝偒偱偡傛偹丅
偳傫側偵慺惏傜偟偄棟榑傪偆偪偨偰偰傕丄幚尡寢壥傗尰幚偲崌傢側偗傟偽丄
擣傔偰傕傜偊側偄丅
偱傕丄悢妛偼偪偑偄傑偡丅
悢妛偱偼丄妋偐偵嬶懱揑側儌僨儖偑偁偭偨曽偑傢偐傝傗偡偄偟丄僀儊亅僕傕傢偒傑偡丅
偱傕丄嬶懱椺偼昁偢偟傕昁梫偱偼側偄偱偡丅
値師尦偱峫偊傞側傫偰偙偲傕偦偆偱偡丅
悢妛偼暔帠傪拪徾壔偡傞妛栤偩偲巚偄傑偡丅
愭傎偳丄悢妛傪傗傞恖偼幮夛偲偺娭傢傝偼峫偊偰偄側偄偲彂偒傑偟偨偑丄
崱偺帪戙偼偦傟偱偼捠梡偟側偄偲巚偄傑偡丅
屆偔偼丄僲亅儀儖偑僟僀僫儅僀僩傪嶌偭偨丄
傾僀儞僔儏僞僀儞偑憡懳惈棟榑傪偆偪偨偰偨丄
斵傜偼偦傟傜偑懡偔偺恖娫傪嶦彎偡傞寢壥偵側傞偲偼柌偵傕巚傢側偐偭偨偱偟傚偆丅
堛妛偺暘栰偵偍偗傞條乆側栤戣丄擼巰丄堏怉丄惗怋偵娭偡傞偙偲側偳丄
椺傪偁偘偨傜偒傝偑側偄偱偡
丅尰嵼丄帺慠壢妛乮悢妛傕娷傔偰乯偵娭傢傞恖娫偼丄恀棟扵媶偩偲尵偭偰丄
幮夛惈傪柍帇偡傞偙偲偼偱偒側偄偲巚偄傑偡丅
恖娫偲偟偰偺椣棟娤傪偟偭偐傝傕偭偰偄側偄偲偄偗側偄偲巚偄傑偡丅
偝偰丄嫵堢偺柺偱悢妛傪偲傜偊傞偲偳偆偐丠丂
惗搆偨偪偵丄悢妛偭偰偍傕偟傠偄偱偟傚偆丄
偲尵偭偰傕傢偐偭偰偼傕傜偊傑偣傫丅
夝偗傟偽妝偟偄丄偲偄偆偙偲偼偁傞偱偟傚偆丅
偟偐偟丄弮悎偵悢妛偺偍傕偟傠偝傪揱偊傞偺偼帄擄偺媄偱擔乆奿摤偟偰偄傑偡丅
悢妛偼壗偺偨傔偵曌嫮偡傞偐丄
偙偺幙栤偵懳偡傞摎偊偼偒傢傔偰擄偟偄偱偡丅
傕偪傠傫丄幚惗妶偵栶棫偨偣傞偨傔偲偄偆偺偑偁傞偱偟傚偆丅
偱傕丄崅峑惗偵偦傟傪偄偆偲丄
乽愭惗丄旝暘抦傜側偔偰傕攦偄暔偼偱偒傞傛丅乿偲惗搆払偼尵偄傑偡丅
巹偼偦偆偼巚傢側偄偗傟偳丄
斵傜偵偲偭偰幚惗妶偲悢妛偼側偐側偐寢傃偮偐側偄偺偱偟傚偆丅
巹偼丄悢妛偵尷傜偢崅峑偱曌嫮偡傞撪梕偼
帺暘偺恖娫惈傪朙偐偵偡傞偨傔偵妛傇偺偩偲惗搆偵偼尵偭偰偄傑偡丅
乮偳偙傑偱揱傢偭偰偄傞偐傢偐傝傑偣傫偗傟偳丒丒丒乯
傕偪傠傫丄傕偭偲愱栧揑偵曌嫮偟偨偄壢栚偑偁傟偽偦傟傪曌嫮偡傞偺偼
摉慠偱偡偗傟偳丄庴尡壢栚偵側偄傕偺偼傗傜側偄丄側傫偰偙偲偵傕側傝偐偹傑偣傫丅
帺暘偺壜擻惈傪暵偞偝偢丄峀偘傞偨傔偵偄傠偄傠側偙偲傪妛傇偺偩偲
丄巹偼尵偄偨偄偱偡丅
丂
悢妛偵偮偄偰尵偊偽丄
愭掱傕偐偒傑偟偨偑侾偮偵偼暔帠傪拪徾壔偡傞偲偄偆偙偲傪妛傇丄
偲偄偆偙偲偩偲巚偄傑偡丅
乮傕偪傠傫帺慠壢妛傪巙偡恖偵偲偭偰偼悢妛偼尵岅偱偡偐傜丄
摉慠岅妛妛廗偼嵟掅尷昁梫偱偡丅乯
傢偗偺傢偐傜側偄偙偲傪偐偒傑偟偨丅俀審傔偵偮偄偰偼傑偨夵傔偰丅
NO.8丂丂6/18丂丂丂丂傒偐傫
尰嵼偺悢妛偼丄暘偐傝偒偭偨偙偲惓偟偄偙偲懄偪丄
岞棟傪婎斦偵棟榑揑傪峔抸偟偰偄偔傕偺偱偁傞丄偦傟備偊偵偙偦丄
弌棃忋偑偭偨棟榑偼乽惓偟偄乿偺偱偡丅
偱偡偐傜丄帺慠尰徾偺愢柧傗擔忢偺暔帠傪棟夝偡傞庤彆偗偵偼
昁偢偟傕側傜側偄偺偼摴棟偩偲巚偄傑偡丅
側偤側傜丄帺慠尰徾傗擔忢偺弌棃帠偵偼晄壜夝側傕偺
乮傑偩枹抦側傞傕偺乯傪傕娷傔偰弌棃忋偑偭偰偄傞偐傜偱偡丅
偙偺偙偲偵傛傝悢妛偑慡偰偺傕偺傪棟夝偡傞摴嬶偲側傝摼側偄強埲偱傕偁傝丄
悢妛偑栶偵棫偨側偄偲尵傢傟偰傕丄
悢妛幰偼暜慠偲偟偰屩傝崅偔丄
榑棟傪傪愊傒忋偘棟榑懱宯傪嶌偭偰偄偔偺偩偲巚偄傑偡丅
NO.9丂丂丂6/19丂丂BRAINMANIA丂丂
儊乕儖桳傝擄偆偛偞偄傑偟偨丅
戝曄嫽枴怺偔攓尒偝偣偰偄偨偩偒傑偟偨丅
偦偙偱巹側傝偺悢妛偵偮偄偰偺峫偊傪偍揱偊偟傑偡丅
暔帠傪榑棟棫偰偰巚峫傪弰傜偡楙廗偵丄
悢妛偑栶棫偭偰偄傞偲巹偼巚偄傑偡丅
検巕擼棟榑傪偆偪棫偰偨儘僕儍乕丒儁儞儘乕僘攷巑傕
擼傪峫偊傞偺偵悢妛傪僼傿乕儖僪偵慖傃傑偟偨丅
偦傟傎偳悢妛偼榑棟棫偰偰峫偊傞偺偵傆偝傢偟偄椞堟偩偲巚偄傑偡丅
幮夛偵弌偨傜堦晹傪彍偒丄嶰妏娭悢偲偐丄懳悢側傫偰偺偼巊偄傑偣傫丅
偟偐偟丄妛惗帪戙偵偦傟傜偺栤戣傪夝偔偺偵巊偭偨峫偊曽傗丄
夝偔偨傔偺恑傔曽丄偦偺夝偒曽偑偄偐偵惓偟偄偐傪愢柧偡傞擻椡側偳偼丄
幮夛恖偵側偭偰傕巊傢傟傞偙偲偱偟傚偆丅
偨偩偟丄偦偺偲偒攟偭偨擻椡偼丄帺慠偲帺暘偺擻椡偵旛傢偭偰偟傑偭偰偄傞偺偱丄
悢妛偺岠壥傪偄傑偄偪堄幆偟偢傜偄偺偱偟傚偆丅
偩偐傜丄彫搰愭惗傕惗搆偵悢妛傪嫵偊傞偲偒偵偼丄
偙偺偙偲傪嫮挷偝傟偨傜偄偐偑偱偟傚偆偐丅
岺妛晹偼丄悢妛偺抦幆傪偄偐偵幮夛偵栶棫偰偰偄偗傞偐傪
尋媶偡傞偲偙傠偲巚偄傑偡丅
慡偔傓偩偲巚偊傞嫊悢傕丄
寁嶼曽朄偵傛偭偰偼岎棳揹棳傪専摙偡傞偺偵栶棫偭偰偄傑偡
乮傎偐偵怓乆偁傝傑偡偑丄曌嫮偟偰偄側偄偺偱乧乯
栤俀偲偟偰乽摢偑傛偄偲偼偳偆偄偆偙偲偐乿傪庢傝忋偘傑偟偨丅
巹側傝偺峫偊傪偡偙偟丄偍揱偊偟傑偡丅
摢偑傛偄丄偲偄偆掕媊偵偮偄偰丄
戝偒偔暘偗偰俁庬椶偁傞偲峫偊傑偟偨丅
侾偮偑乽婰壇椡乿丅傑偁丄偙傟偼妛峑偺曌嫮偱妎偊傞傛偆側傕偺
乮戝壔夵怴偼俇係俆擭側傫偐乯丅
俀偮栚偑乽敪憐椡乿丅
偙傟偼抦幆傪慻傒崌傢偣偰壗偐偵栶棫偰傛偆偲偡傞偙偲丅
俁偮栚偑乽憐憸椡乿丅
柍偐傜桳傪嶌傝弌偡丄偲偄偆偺偑憡墳偟偄偱偟傚偆丅
乽敪憐椡乿偲乽憐憸椡乿偼摨偠傕偺偩偲傕峫偊傜傟傑偡偑丄
巹偼偁偊偰俀偮偵暘偗傑偟偨丅
愢柧偼屻夞偟偲偄偆偙偲偱丄偱偼丅
NO.10丂丂丂6/23丂丂丂MK142857
彫搰弤巕丂愭惗丄偙傫偵偪偼丅
怴嶌僆儕僕僫儖栤戣傪嶌傝傑偟偨偺偱丄憲傝傑偡丅
栤戣係
f(x)=x2-4x+6偲偡傞偲偒丄
師偺曽掱幃偼偄偔偮偺幚悢夝傪帩偪傑偡偐丅
丂丂丂 f(f(f(f(f(x)))))=2
栤戣俆
師偺俀偮偺忦審傪摨帪偵枮偨偡嵟彫偺帺慠悢傪媮傔偰壓偝偄丅
忦審侾丂奺埵偺悢偑奆摍偟偄丅
忦審俀丂侾偐傜俋傑偱偺俋偮偺帺慠悢偺偆偪丄
偁傞侾偮傪彍偄偨俉偮偺帺慠悢偺岞攞悢偱偁傞丅
NO.11丂丂6/24丂丂丂Junko
崱夞偺栤戣傕側偐側偐偄偄偱偡偹偊丅
偳偆傗偭偰丄栤戣傪敪埬偡傞偺偐僐僣傪嫵偊偰傕傜偄偨偄側偁丅
偝偭偦偔丄夝偄偰傒傑偟偨丅
栤戣係丂
幚悢夝偼侾偮丄俀偱偡偹丅
偙偺曽掱幃偼俁俀師曽掱幃偱夝偺俀偼俁俀廳夝偱偡偹丅
捈慄y=x忋偺揰乮俀丆俀乯偵y=f(x)偺僌儔僼丄
曻暔慄偺捀揰傪帩偭偰偒偨偲偄偆偲偙傠偑億僀儞僩偱偡傛偹丅
偝偰丄偙偺栤戣傪敪揥偝偣偰
乮悢妛傪傗傞恖偼偡偖堦斒壔偟偨偑傞廗惈偑偁傞傫偱偡丅乯
乽f(x)=x2-4x+6偲偡傞偲偒丄師偺曽掱幃偼偄偔偮偺幚悢夝傪帩偪傑偡偐丅
f(f(f(f(f(x)))))=a丂乿偲偡傞偲丄偳偆偱偟傚偆丅
a=2偺働亅僗偼偄偄偱偡傛偹丅
嘆a<2偺応崌
丂y=f(x)偺僌儔僼偲y=a偺僌儔僼偼岎揰傪帩偪傑偣傫偐傜幚悢夝偼懚嵼偟側偄丅
嘇a>2偺応崌
丂y=f(x)偺僌儔僼偲y=a偺僌儔僼偼岎揰傪俀偮帩偪傑偡丅
偮傑傝幚悢夝偼俀偮偁傞傢偗偱丄
偙傟傪兛1丄兝1偲偡傞偲
乮兛1亙兝1乯
兛1亙俀丄俀亙兝1偲側傞丅
丂師偵f(f(f(f(x))))=兛1丄
f(f(f(f(x))))=兝1
側傞俀偮偺曽掱幃傪峫偊傞偲丄
慜幰偼兛1亙俀傛傝丄嘆偲摨條幚悢夝偼側偄丅
屻幰偼俀亙兝1侾傛傝幚悢夝傪俀偮帩偮丅
偙傟傜傪兛2丄兝2 偲偡傞偲
乮兛2亙兝2乯
兛2亙俀丄俀亙兝2偲側傞丅
偲丄偄偆傛偆偵俆夞孞傝曉偡丅
廬偭偰丄嵟廔揑偵偼幚悢夝偼兛5丄兝5丂 偺俀偮偲側傞丅
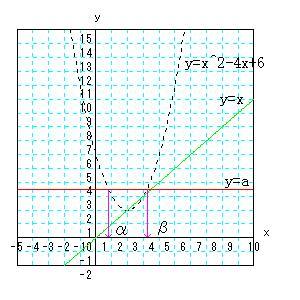
栤戣俆丂
偙傟偼丄慜夞偺Weekend丂Mathematics丂俆丂僇亅僪偺栤戣
(僽儔僂僓偺Back儃僞儞偱栠偭偰偒偰偹丅)偺墳梡栤戣偲偟偰嵟揔両
丂偝偰丄偢傜偢傜偲暲傇悢帤偱偡偑丄
NO.12丂丂6/24丂丂K.Y.丂丂丂
栤戣係偵偮偄偰杔傕峫偊偰傒傑偟偨丅
f(X)=f5 (X)偲偐偔丠
傑偁丄偐偔偲偟偰
f1 (X)=x2-4x+6
f2 (X)= (f1 (X))2-4( f1 (X))+6
f3 (X)= (f2 (X))2-4( f2 (X))+6
乧
fn (X)= (fn-1 (X))2-4( fn-1 (X))+6
偙偙偱丄fn (X)=2偲偡傞偲丄乧嘆
(fn-1 (X))2-4( fn-1 (X))+6=2傛傝丄
fn-1 (X)=2乧嘇
嘆嘇傛傝丄fn (X)= fn-1 (X)
廬偭偰丄f5 (X)= f (X)=2
x=2乮廳夝乯
 栠傞
栠傞