Weekend Mathematics/問題/問題98
98.消えた数
たろうくんは、1から順番に1,2,3,4,5,・・・とある数までを黒板に書きました。 じろうくんがその中の1個の数を消してしまいました。 すると残りの数の平均は、590/17になりました。じろうくんの消した数はいくつですか。
算数オリンピックに挑戦
'00~'03年度版
算数オリンピック委員会編
2000年第9回算数オリンピックトライアル問題
解答・その1
(ペンネ-ム:浜田 明巳)
答は,
1~69の中から55を消す事により,平均は590/17になる
です.
解答その1.
次のエクセルのマクロで解きました.
約分して590/17になるのだから,最初書いた数は1~17m+1(mは自然数)である.このmと,消す数kを求めればよい.あとはシラミつぶし計算である.
Option Explicit
Const m As Long = 200 '********
Sub Macro1()
Sheets("Sheet1").Select
Range("A1").Select
Dim n As Integer
Dim k As Integer
Dim wa As Long
Dim g As Long
Dim kosuu As Long
Dim j As Integer
kosuu = 0
For n = 17 * 1 + 1 To 17 * m + 1 Step 17
For k = 1 To n
wa = -k
For j = 1 To n
wa = wa + j
Next j
g = GCM(wa, n - 1)
If wa / g = 590 And (n - 1) / g = 17 Then
kosuu = kosuu + 1
Cells(kosuu, 1).Value = k
Cells(kosuu, 2).Value = n
End If
Next k
Next n
MsgBox Str(17 * m + 1) + "以下の数では,答は以上の" + Str(kosuu) + "個です.", vbOKOnly
End Sub
Private Function GCM(ByVal a As Long, ByVal b As Long) As Long '最大公約数
If b = 0 Then
GCM = a
Else
GCM = GCM(b, a Mod b)
End If
End Function
しかしこの方法では,k≦17×20+1=3401と,非常に狭い範囲でしか答を求めていない.そこで,もう少し広い範囲で求める為に,次の工夫をした.
解答その2.
もう一つの方法で,エクセルのマクロで解きました.
解答その1のm,kを求める.平均を求めると,
[{1+2+………+(17m+1)}-k]/(17m)
={(17m+1)(17m+2)/2-k}/(17m)
={(17m)2+3・17m+2-2k}/(2・17m)=590/17
∴289m2+51m+2(1-k)=2m・590
∴289m2-1129m+2(1-k)=0
∴m=[1129±{11292-4・289・2(1-k)}1/2]/(2・289)
={1129±(1272329+2312k)1/2}/578
故に1272329+2312kが平方数になり,mが自然数となり,1≦k≦17m+1となるm,kを求めればよい.あとはシラミつぶし計算である.
Option Explicit
Sub Macro2()
Sheets("Sheet1").Select
Range("A1").Select
Dim m As Long
Dim k As Long
Dim D As Long
Dim Dd As Long
Dim fugou As Integer
Dim kosuu As Integer
kosuu = 0
For k = 1 To 928292 '********
D = 1272329 + 2312 * k
Dd = Int(Sqr(D))
If Dd * Dd = D Then
For fugou = 1 To -1 Step -2
m = Int((1129 + fugou * Dd) / 578)
If m >= 1 And k <= 17 * m + 1 And 289 * m * m - 1129 * m + 2 * (1 - k) = 0 Then
kosuu = kosuu + 1
Cells(kosuu, 1).Value = k
Cells(kosuu, 2).Value = 17 * m + 1
End If
Next fugou
End If
Next k
End Sub
しかし,この方法でもぎりぎりk≦928292までの答である.そこで使うソフトを替えてみた.
解答その3.
解答その2の方法を,UBASICを使って解きました.
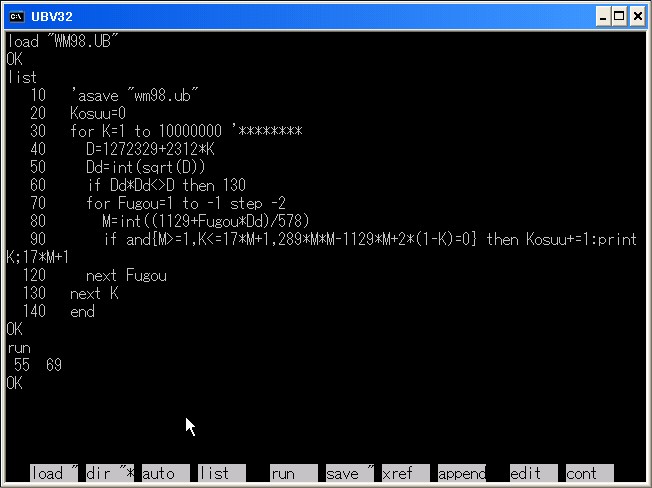
これでk≦10000000での答となった.時間の関係でこのくらいが妥当であろうか.
数学的には,すべてのmについて計算しなければならず,無限大の時間がかかるので,解けない.これがコンピュータの限界なので,仕方がないでしょう.
解答・その2
(ペンネ-ム:すたこらさっさ)
/* * 作成日: 2005/02/01 * */ package quiz; /** * 98.消えた数 * たろうくんは、1から順番に1,2,3,4,5,・・・とある数までを黒板に書きました。 * じろうくんがその中の1個の数を消してしまいました。 * すると残りの数の平均は、590/17になりました。じろうくんの消した数はいくつですか。 * * 算数オリンピックに挑戦 * '00~'03年度版 * 算数オリンピック委員会編 * 2000年第9回算数オリンピックトライアル問題 * */ public class Question0098 { /** 分子 */ private static int numerator = 590; /** 分母 */ private static int denominator = 17; public static void main(String[] args) { /* 数値の加算ワーク */ int x = 0; /* 数値の最大値 */ int y = 0; /* 17の倍数カウント */ int z = 0; /* 答え */ int answer = 0; while(true) { z++; int i = 0; /* 平均値が590/17になるには数値の最大は17の倍数+1になる */ for(i = y + 1; i < ( z * 17 ) + 1; i++) { x = x + i; } y = i; /* 数値の合計と590の倍数の差を求める */ answer = x - ( 590 * z); /* * 上記の差がゼロより大きく最大数より小さければその数を * 消すことは可能 */ if(answer > 0 && answer < y) { // System.out.println("number end = " + y); // System.out.println("sum numbers = " + x); // System.out.println("answer = " + answer); break; } } System.out.println("1から" + y + "までを足した" + x + "から" + answer + "を引き" + y + "マイナス1で割れば平均がでる"); int a = y - 1; int b = x - answer; System.out.println("1から" + y + "までを足した" + x + "から" + answer + "を引いた" + b + "も" + y + "マイナス1の" + a + "も" + z + "で割り切れる"); System.out.println(b + "÷" + z + "=590"); System.out.println(a + "÷" + z + "=17"); System.out.println("よって" + b + "/" + a + "は590/17に約分できる。"); } }
解答・その3
(ペンネ-ム:寺脇犬)
590/17を 34と12/17 とか 小数で表したりしないで このままで考える。 平均値 590/17より、 全体は 590でこれは17の数字からできていると考えると 問題文より 最初は18個で それらは連続数であって その和を求めると
18×19×1/2 = 171
となるが この数だと 1個減じた全体の数590より 小さいので ダメ
そこで今度は、 平均値590/17 を変形した同値の
1180/34 , 1770/51 , 2360/68 , 2950/85 , 3540/102 , ・・・・
を考える。
まず 1180/34の場合
590/17と同じように考えると 1個減じない元の数の和は
35×36×1/2= 630
これも1個減じた数の和の方が大きいので これもダメ
次に 1770/51の場合 これも
52×53×1/2 = 1378
だから 同じくダメ
2360/68の場合
69×70×1/2 = 2415
これは 1個減じた全体数2360より 大きいので まずは OK で保留にして あとで考える。
次は 2950/85の場合
86×87×1/2 = 3741
だが これは1個減じた全体数2950より 大きいので問題の条件に適すが
3741-2950 =791より
抜いた数は791となって これは この場合の全体数のあつまりである 1から86までには 含まれてないので やっぱりダメ
その次は 3540/102の場合
これも同様に考えて 元の数の和は
103×104×1/2 = 5356
で5356- 3540 =1816 より抜いた数は 1816になるから これは この場合の 1から103の中には含まれないので ダメ
さてこの後も 590/17と同値で、 分母が102より大きくなっていくと 抜いた数はその構成している連続数の集まりの中から 乖離していくので 問題に適しない。 こうして考えていくと 結局問題に適するのは平均値 2360/68の場合だけと分る。 以後この場合を検討する。
2360/68が 1個抜いた後の平均値とすると もとの数の集まりは 1から 69までとなって その数の和は
69×70×1/2 = 2415
そして抜いた数は
2415-2360= 55
55は 1から69の中に 含まれているので これが答えです。
解答・その4
(ペンネ-ム:内海 育)
(答) 55
(過程)
ある正の整数をn、消した数をxとすると)
{n(n+1)/2-x}/(n-1)=590/17・・・・・①,
∴17n2-1163n+1180=34x
1≦x≦nゆえ 34≦17n2-1163n+1180≦34n
∴0≦17n2-1163n+1146 and 17n2-1197n+1180≦0
∴n=68 or 69
①式より、(n-1) は17の倍数ゆえn=69
よって、①式より x=55
解答・その5
(ペンネ-ム:FIVEILAND)
考え方 自然数の和とその平均については、あまり知識が無いのでいくつかの規則 について考えてみました。
1.
1 平均 1 1+2=3 平均 1.5 1+2+3=6 平均 2 1+2+3+4=10 平均 2.5
…個数n+1に対して平均は1/2ずつ増加する。
2.
7までの和について 個数7-1=6について6は約数が多いので色々な 意味で規則性が見出せるかなと思いましたが後で考えてみると、特に意味はありませ んでした。
7までの和は、 1+2+…+6+7=7×8×1/2=28 平均4
1がない場合の平均 27÷6=4・3/6=4・1/2
2がない場合の平均 26÷6=4・2/6=4・1/3
3がない場合の平均 25÷6=4・1/6
4がない場合の平均 24÷6=4
5がない場合の平均 23÷6=3・5/6
6がない場合の平均 22÷6=3・4/6=3・2/3
7がない場合の平均 21÷6=3・3/6=3・1/2
ここまででわかることは、ある数までの個数-1の平均は、①本来の 平均±1/2の中にある。②本来の個数-1での平均値には必ず個数-1の約数が分母に含 まれている。あたりまえか?
ここまでわかったことを踏まえて、590/17について考えて見ます。
590/17=34・12/17
本来の平均は、34・12/17-1/2から34・12/17+1/2の間にある。つまり 34・7/34から35・7/34のなかにある。ところが自然数の和の平均は1から始 まり1/2づつ増加するので、34.5か35であることがわかる。
この場合の自然数の個数は、69か70になる。
590/17の時の個数は、68か69ということになるが、17を約数に持つものは68である。
したがって本来の個数は69であることがわかる。
590/17×68=2360 69×70/2=2415 2415-2360=55
答え じろうくんが消した数は 55
解答・その6
(ペンネ-ム:moko)
平均は590/17ということは ある数は17の倍数+1となる
1) ある数=18とすると
1から18までの合計=171
残りの平均=(171-χ)/17=590/17 χ=-419 となる
2) ある数=35とすると
1から35までの合計=630
残りの平均=(630-χ)/34=1180/34 χ=-550 となる
同様にして計算するとχ>0になるのは
ある数=69
1から69までの合計=2415
残りの平均=(2415-χ)/68=2360/68 χ=55 となる
またある数=86とすると
1から86までの合計=3741
残りの平均=(3741-χ)/34=2950/34 χ=791 となり
86より大きくなるので不適
よって答えは 55
解答・その7
(ペンネ-ム:やんま)
解答・その8
(ペンネ-ム:三角定規)
たろうくんがNまで書き,じろうくんが数m(1≦m≦N )を消したとする。
題意より,
∴ 17{N(N+1)-2m}=2・590・(N-1) … ②
17と590は互いに素だから,N-1 が17を素因数としてもつ。
よって, N-1=17k ∴ N=17k+1 … ③
③を②に戻して整理すると,
(17k+1)(17k+2)-2m=2・590・k … ④
(1) k=1 のとき 18・19-2m<18・19<2・590・1 で,④を満たさない。
(2) k=2 のとき 35・36-2m<35・36<2・590・2 で,④を満たさない。
(3) k=3 のとき 52・53-2m<52・53<2・590・3 で,④を満たさない。
(4) k=4 のとき 69・70-2m=2・590・4=4720 ∴ m=(4830-4720)/2=55
(5) k≧5のとき,④より
このmは,③で定まるNを大きく超え,題意を満たさない。
以上より,じろうくんが消した数は,55 …[答]
解答・その9
(ペンネ-ム:佐野允信)
1からnまで書き、数iを消したとする。i以外の(n-1)個の数の平均をαとおくと、
が成り立つ。1≦i≦nだから、
今、α=34+12/17だから、(2)より
nは正の整数だから、(3)より
n=68,69 ・・・(4)
さらに(1)より、α(n-1)=(590/17)(n-1)は、正の整数だから、(4)より
n=69 ・・・(5)
従って、
i =(1+2+・・・+n)ーα(n-1) (∵(1)より) (1/2)×69×70ー(590/17)×68 (∵(5)かつα=590/17より) 55
よって求める数55である。・・・(答)
解答・その10
(ペンネ-ム:巷の夢)
たろうの書いた数を1~Nまでとし、じろうの消した数をXとします。すると、じろうが消す前の数の平均は(N+1)/2となります。次にXのみ消した場合の平均は前の合計からXを引き、個数N-1で割ればよいので
〔N(N+1)/2 -X〕/(N-1) = 590/17 となります。
即ち、N-1が17の倍数であることが必要です。つまり、17、17×2、17×3、17×4、・・・となります。
又、上記式を変形すると、34X=17N(N+1)―1180(N-1)となります。
ところでN≧Xが必要ですから、34N≧17N(N+1)―1180(N-1)となり、 これよりNは1から69までの自然数となります。
そこで先程の17の倍数条件をあてはめて解くと、N=69、X=55を得ます。 因って、じろうの消した数は55となります。
解答・その11
(ペンネ-ム:高橋道広)
たろうくんが書いた数字の個数を(17n+1)個とします。
じろうくんが数を消したあとの4n個の数の平均が590/17ですからその合計は 590/17×17n=590n となります。
この数は 1~17nまでの数の和より 少なくない(じろうくんが消した数の最大は17n+1)ので
590n≧17n(17n+1)/2 から
17n+1≦590×2/17=69.4...
17n≦70
n≦4
一方この数は 2~17n+1までの数の和より 大きくない(じろうくんが消した数の最小は1)ので
590n≦17n(17n+3)/2
17n+3≧590×2/17=69.4...
17n≧67
n≧4
よって n=4 たろうくんの書いた数の和は (17×4+1)(17×4+2)/2=2415
じろうくんが消した数を除いた和は 590×4=2360
このことから じろうくんの消した数は 55 となります
17n+1 とするところが ずるいでしょ
みんな たぶんそうしてるでしょうけど(^_^;)
解答・その12
(ペンネ-ム:小学名探偵)
答え 55
590/17=34+12/17から、もし消した数を加えたら、その平均は35あたりになると予想 します。
69*70/(2*69)=35の可能性を考えます。
69-1=68=17*4なので、消した数をxとして、 (69*35-x)/68=590/17=2360/68 これを整理して、 2415-x=2360からx=55が求められました。
1からnまでの合計=n*(n+1)/2 この平均mは、最初の1と最後のnの和の平均に等し く、(n+1)/2です。
さて、1からnまでの整数の中から、ある数xを消したとき、残りの平均は
a={n*(n+1)-2x}/2(n-1)}
です。 aの範囲を考えてみましょう。 aの値はx=nのときに(一番大きな数nを消したとき)最小になります。aの最小値=n/2 つまり、1から(n-1)までの平均がaの最小値です。 aの値はx=1のときに(一番小さな数1を消したとき)最大になります。aの最大値 =(n+2)/2 つまり、1から(n+1)までの平均がaの最大値です。 (2からnまでの平均は、1からn+1までの平均と等しいですね)
以上から、n/2≦a≦(n+2)/2 または
n≦2a≦(n+2)
この問題では、2a=68+24/17=69+7/17なので、n=68か69になります。
ところで、n-1は17の倍数であるので、n=68は不適、n=69です。
以下、省略します。
解答・その13
(ペンネ-ム:はじめ先生)
整数問題の基本はやはり「上手く範囲を絞る」ことでしょうね。
解答・その14
(ペンネ-ム:夜ふかしのつらいおじさん)
答は55です。
たろうくんの書いた数を1からnとし、じろうくんの消した数をkとします。
(0<k<(n+1)です)
すると、
{n(n+1)/2-k}/(n-1)=590/17
整理して、
{n(n+1)-2k}/(n-1)=1180/17 ・・・ (1)
ここで右辺と等しい分数をいくつか考えます。
1180/17
=2360/34
=3540/51
=4720/68
=5900/85
=・・・・
(1)の左辺の分母と比較してnの値は、
18、35、52、69、86、・・・・
などが考えられます。それぞれ、n(n+1)の値は、
342、1260、2756、4830、7482、・・・・
次にこれらのn(n+1)の値からそれぞれの分子の値を引き2で割ってkの値を求めると、
-419、-550、-392、55、791、・・・・
この中で、0<k<(n+1)を満たすのは55です。
解答・その15
(ペンネ-ム:ダイヤモンドダスト)
平均が590/17だから、分母分子ともに何倍かして、得られる数に近い数がある数n。
ここで、分母分子をそれぞれ4倍ずつすると2360/68
1からnまでの総和は、n(n+1)/2であるから、
ここで、n=69とすると、69(69+1)/2=2415
2415-2360=55
よって求める答えは、1から69までの総和であり、消えた数は、55となる。
解答・その16
(ペンネ-ム:やなせ)
さて前ふりです。
1から連続した数値の平均を求めるのは、 なぜか(最大数値+1)÷2=平均のように 簡単な式で求めることが出来ます。
数字を限定して一個消した場合の平均は
最大平均
合計から最小数値(この場合は1)引いて残りの 個数(最大数値ー1)で割った平均は なぜかこれ又(最大数値+2)÷2=平均の様に 簡単な式で求めることが出来ます。
最小平均
更に合計から最大数値を引いた価を残りの 個数で割った価は最大数値÷2=平均になりますねぇ
いつものごとく何でこうなるかは?ですのでつっこまないでくださいね。 以上のことをふまえて
本題です。
問題を考えてみると平均が590÷17=34.70588・・に なるとのことだから
最初の数字(これは1に決定している)を消した場合の 平均が>34.70588で 最後の数字(最大の数字)を消したときの 平均が<34.70588になる処を見つければ 旨く行くのではと考えました。
勝手な前ふり方式から 1~70辺りの連続した数値に目星をつけて確かめてみると
1~68の場合
大平均は(68+2)÷2=35 小平均は68÷2=34
1~69の場合は
大平均は(69+2)÷2=35.5 小平均は69÷2=34.5
1~70の場合は
大平均は(70+2)÷2=36 小平均は70÷2=35
確かにいい感じですねぇ(笑)
1~70の場合はどっちも35以上なのでやめにして 次の1~69までを計算してみました
ここからは得意の虱潰しの手計算(本当はエクセル使いましたが)でやると 1~69までの連続数字から55を消した場合の平均が
(1+2+・・・・・・・・・+69)=2415
2415-55=2360
2360÷68=34.70588・・・=590/17
最終お答え
1から69までの連続した数字から55を消した時
解答・その17
(ペンネ-ム:JSミル)
たろうくんが最初に書いた数を1~n,じろうくんが消した数をxとすると,平均を 出すための分母はn-1であり,これが17の倍数である.従って,nの候補は18,35, 52,69.......17×k+1となる.場合分けで,それぞれの合計を調べ,平均の分子で ある590kと合わせていくと,n=69の時,1~nまでの合計は2415で,平均の分母 は590×4=2360であり,2415-2360=55となり,じろうくんの消した数は55である.
答え:55
解答・その18
(ペンネ-ム:challenger)
「消えた数」の問題ですが、次のように考えました。
1からn-1までの合計は(n-1)n/2だから平均はn/2
2からnまでの合計は(n-1)(n+2)/2だから平均は(n+2)/2
したがってn/2<=590/17<=(n+2)/2からn=68、69
消した数をxとすると、
n=68のとき
{(1+2+・・・+68)-x}/67=590/17で条件をみたすxは存在しない。
n=69のとき
{(1+2+・・・+69)-x}/68=590/17よりx=55
解答・その19
(ペンネ-ム:Mr.X)
オーソドックスに
(n(n+1)/2-n)/(n-1)≦590/17≦(n(n+1)/2-1)/(n-1)
かつ (n-1) が 17 の倍数
17n≦1180≦17(n+2)
かつ (n-1) が 17 の倍数
1136≦17n≦1180
かつ (n-1) が 17 の倍数
67≦n≦69
かつ (n-1) が 17 の倍数
n-1=4×17
n=69
(69×70/2-a)/68=590/17
a=69×70/2-4×590
答は 55 です。
解答・その20
(ペンネ-ム:Toru)
たろう君が 1,2,3,4,5,・・・,Nまで書いたことにする。
じろう君が1個消した時の残りの和をSとすると、残りの数の平均S/(N-1)=590/17よ り17S=590(N-1)、左辺は17の倍数だから、右辺も17の倍数であるが、590と17は互い に素であるから、N-1は17の倍数-----1)
1個消した残りの平均は、Nを消した時が最小で(1+(N-1))/2=N/2、1を消した時が最 大で(2+N)/2=N/2+1 すなわちN/2≦590/17≦N/2+1、590/17=34.7---だからこれを満た すNは N=68 or 69 ------2)
1)2)よりN=69
このとき S=68×590/17=2360,
1,2,3,4,5,・・・,69の和は(1+69)×69/2=2415
だからじろう君の消した数は 2415-2360=55 答え55
解答・その21
(ペンネ-ム:なか)
ある数をnとする。
1~nのうち一番小さな1を消すと、2~nが残りその平均はn/2+1。
1~nのうち一番大きなnを消すと、1~n-1が残りその平均はn/2。
つまりどれを消しても、残る数の平均はn/2~n/2+1の範囲に納まる。
そこで、n/2≦590/17≦n/2+1 → n=68またはn=69。
ここで、残った数の平均の分母が17であることにより、残った数の個数、
n-1が17の倍数でなければならないので、n=69に絞られる。
さて、1~69の合計は、 69×70÷2=2415
一方、残った数の和は、590/17×68=2360
よって、消えた数は、2415-2360=55
(答)55
解答・その22
(ペンネ-ム:杖のおじさん)
答え 55 です。
連続した自然数の合計の平均は整数又は0.5が端数として付きます。
問題は 590/17=34.70588235
従って34.70588235 以上で次の整数又は次の0.5の端数が付いた整数以下
いずれか低い方なので35以下の平均になります。最大数字は35*2-1=69となります。
69までの自然数字の合計69*(69+1)/2=2415から端数590/17*68=2360を引きます。
2415-2360=55 となります。
検証
1・2・3・4……69
までの合計 69*70/2=2415
55を消す2415-55=2360
2360/68=590/17で証明できます。
解答・その23
(ペンネ-ム:けいたろう)
1からnまでの和はn(n+1)/2なので、1からnまでの数の平均は(n+1)/2です。 平均は590/17=34.70…
また平均が590/17ということは消されたあとの個数は17の倍数であると思われるのでn=68、 n+1=69です
590/17=2360/68であり、1から69までの和は(69+70)/2=2415なので、 2415-2360=55が消された数字です
解答・その24
(ペンネ-ム:kiyo)
解答
34.5<590/17<35
から、1~69まで書いたことがわかる。
消された数をXとすると、
(35*69-X)/68=590/17
X=55
となる。
答え 55。
解答・その25
(ペンネ-ム:teki)
答え 55
考え方
1から順番に書かれた数から1個消したものの平均が590/17になるので、消さ れた後の数字の個数は17の倍数です。
よって、元の数字の個数は17n+1個となります。
これが分かれば、後は∑を使えば答えは出てきます。
元の数字は1から69まで書かれ、その合計は2415、ここから55が消されて、 残る数字の合計が2360、これを68でわれば、590/17となります。
数学的には、方程式を使えば、出てくるんでしょうが、この程度であれば、試行錯誤 して小学生にも解けそうです。
正解者
夜ふかしのつらいおじさん 巷の夢 杖のおじさん やなせ すたこらさっさ 小学名探偵 Toru なか kiyo teki 佐野允信 Mr.X 浜田 明巳 けいたろう 内海 育 寺脇犬 FIVEILAND ダイヤモンドダスト はじめ先生 JSミル 高橋道広 moko 三角定規 やんま challenger
たくさんの方から解答をいただきました。心から感謝しております。
じろうくんが数字をひとつ消したとしても、その平均が 590/17≒34. ・・・であることから、ある数はおよそ70と検討がつきます。 かつ平均値の分母が17であることから、ある数は、自然数kを用いて、 17k+1と表せる数だということになります。とすると、答えは69ですね。 まずは、方程式をたててどうこうするよりも、答えの検討をつけるということが大事なことかなたお思います。 これで解答がかなりすっきり組み立てられると思います。 ただし、解答をきちんとした形で検証する必要があるのは当然ですね。

 E-mail
E-mail
 top
top