96.四角形の面積
たて4cm、横6cmの長方形ABCDがあります。 図のように、それぞれに辺の上に点E、F、G、Hをとり、 H、Fを結んだ線の上に点Pをとり、E、Gと結びます。
四角形AEPHの面積が5cm2のとき、 四角形PFCGの面積を求めなさい。
Weekend Mathematics/問題/問題96
96.四角形の面積
たて4cm、横6cmの長方形ABCDがあります。 図のように、それぞれに辺の上に点E、F、G、Hをとり、 H、Fを結んだ線の上に点Pをとり、E、Gと結びます。
四角形AEPHの面積が5cm2のとき、 四角形PFCGの面積を求めなさい。
算数オリンピックに挑戦
'00〜'03年度版
算数オリンピック委員会編
2000年第9回算数オリンピックトライアル問題
解答・その1
(ペンネ−ム:米ぽん)
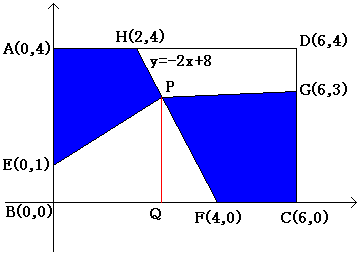
関数(座標)で考えました。もっといい方法があると思うですが・・・・。
Bを座標原点として、線分HF上の点PをP(x,y)とする。
直線HFを一次関数として、P(x,y)は、
y=-2x+8 ・・・・・・・・・(1)
また、四角形ABFH=(2+4)*4/2=12、四角形AEPH=5より、
四角形EBFP=四角形ABFH-四角形AEPH=12-5=7
点Pから線分BCへおろした垂線と線分BCとの交点をQとして、
四角形EBFP=四角形EBQP+三角形PQF=(1+y)x/2+(4-x)y/2=7
これをまとめると、
x+4y=14 ・・・・・・・・(2)
(1)(2)から、
点P(x,y)=(18/7 , 20/7) ・・・・・・・(3)
三角形HPD=(4*(4-20/7))/2=16/7
三角形DPG=(1*(6-18/7))/2=12/7
四角形PFCG=四角形FCDH-三角形HPD-三角形DPG
四角形FCDHは、
四角形FCDH=(2+4)*4/2=12
よって、四角形PFCGは、
四角形PFCG=四角形FCDH-三角形HPD-三角形DPG=12-16/7-12/7=8
答えは8cm2
解答・その2
(ペンネ−ム:内海 育)
(答)8cm2
(過程)点Pを通り長方形の辺に平行な線とAB,BC,CD,DAとの交点をQ, R,S,Tとし、PQ=a[cm],PT=b[cm],四角形PFCGの面積=x[cm2]と置 く。
題意より (3a+2b)/2=5。∴3a+2b=10
x={3(6-a)+2(4-b)}/2={26-(3a+2b)}/2=8
解答・その3
(ペンネ−ム:<匿名>)
AEPH面積=三角面積AHE+三角面積EPH
三角面積AHE=3
三角面積EPH=2
EとGからそれぞれHFに垂足する線 ER、GQを作る
ER長さ=GQ長さ
三角面積EPH=三角面積GPH=2
PFCG面積=CDHF面積−三角面積DGH−三角面積GPH=12―2−2=8
解答・その4
(ペンネ−ム: 浜田 明巳)
解答その1.
次のVISUAL BASICのプログラムにより,面積は8cm2であることが解ります.
Option Explicit Sub Form_Load() Dim waku As Double waku = 1 Picture1.Scale (-waku, 5 + waku)-(6 + waku, -1 - waku) Picture1.BackColor = vbWhite Picture2.BackColor = vbWhite Picture2.Picture = LoadPicture("gazou96a.gif") Picture3.BackColor = vbWhite End Sub Sub Command1_Click() Dim Ax As Double Dim Ay As Double Dim Bx As Double Dim By As Double Dim Cx As Double Dim Cy As Double Dim Dx As Double Dim Dy As Double Dim Ex As Double Dim Ey As Double Dim Fx As Double Dim Fy As Double Dim Gx As Double Dim Gy As Double Dim Hx As Double Dim Hy As Double Dim Px As Double Dim Py As Double Dim Pxx As Double Dim Pyy As Double Dim Px_min As Double Dim Px_max As Double Dim Px_min0 As Double Dim Px_max0 As Double Dim kizami As Double Dim menseki As Double Dim a(1) As Double Dim b(1) As Double Dim c(1) As Double Dim h(1) As Double Dim HE As Double Dim GF As Double Dim PFCG As Double Dim sa As Double Dim min As Double Dim dankai As Integer Dim j As Integer ' Ax = 0 Ay = 4 Bx = 0 By = 0 Cx = 6 Cy = 0 Dx = Cx Dy = Ay Ex = 0 Ey = Ay - 3 Fx = 4 Fy = 0 Gx = Dx Gy = Dy - 1 Hx = 2 Hy = Ay HE = Sqr((Ex - Hx) * (Ex - Hx) + (Ey - Hy) * (Ey - Hy)) GF = Sqr((Fx - Gx) * (Fx - Gx) + (Fy - Gy) * (Fy - Gy)) Px_min0 = Hx Px_max0 = Fx 'HE:y=(Ey-Hy)/(Ex-Hx)*(x-Hx)+Hy -> a0*x+b0*y+c0=0 a(0) = Hy - Ey b(0) = Ex - Hx c(0) = Hx * Ey - Ex * Hy 'GF:y=(Fy-Gy)/(Fx-Gx)*(x-Gx)+Gy -> a1*x+b1*y+c1=0 a(1) = Gy - Fy b(1) = Fx - Gx c(1) = Gx * Fy - Fx * Gy kizami = 0.1 min = 10000 For dankai = 1 To 14 If dankai = 1 Then Px_min = Px_min0 Px_max = Px_max0 Else Px_min = max2(Pxx - kizami, Px_min0) Px_max = min2(Pxx + kizami, Px_max0) kizami = kizami * 0.1 End If For Px = Px_min To Px_max Step kizami Py = (Fy - Hy) / (Fx - Hx) * (Px - Hx) + Hy For j = 0 To 1 h(j) = Abs(a(j) * Px + b(j) * Py + c(j)) / Sqr(a(j) * a(j) + b(j) * b(j)) Next j sa = Abs(0.5 * (Hx - Ax) * (Ay - Ey) + 0.5 * HE * h(0) - 5) If min > sa Then min = sa Pxx = Px Pyy = Py PFCG = 0.5 * (Cx - Fx) * (Gy - Cy) + 0.5 * GF * h(1) Picture3.Cls Picture3.Print "四角形PFCG="; PFCG; "cm2(?), |四角形AEPH-5|="; min End If Picture1.Cls Picture1.Line (Ex, Ey)-(Pxx, Pyy), vbGreen Picture1.Line -(Gx, Gy), vbGreen Picture1.Line (Ax, Ay)-(Bx, By), vbBlack Picture1.Line -(Cx, Cy), vbBlack Picture1.Line -(Dx, Dy), vbBlack Picture1.Line -(Ax, Ay), vbBlack Picture1.Line (Hx, Hy)-(Fx, Fy), vbBlue Picture1.Line (Ex, Ey)-(Px, Py), vbBlue Picture1.Line -(Gx, Gy), vbBlue Picture1.CurrentX = Ax Picture1.CurrentY = Ay Picture1.Print "A" Picture1.CurrentX = Bx Picture1.CurrentY = By Picture1.Print "B" Picture1.CurrentX = Cx Picture1.CurrentY = Cy Picture1.Print "C" Picture1.CurrentX = Dx Picture1.CurrentY = Dy Picture1.Print "D" Picture1.CurrentX = Ex Picture1.CurrentY = Ey Picture1.Print "E" Picture1.CurrentX = Fx Picture1.CurrentY = Fy Picture1.Print "F" Picture1.CurrentX = Gx Picture1.CurrentY = Gy Picture1.Print "G" Picture1.CurrentX = Hx Picture1.CurrentY = Hy Picture1.Print "H" Picture1.CurrentX = Px Picture1.CurrentY = Py Picture1.Print "P" Next Px Next dankai Picture3.Cls Picture3.Print "四角形PFCG="; PFCG; "cm2, |四角形AEPH-5|="; min Picture1.Cls Picture1.Line (Ax, Ay)-(Bx, By), vbBlack Picture1.Line -(Cx, Cy), vbBlack Picture1.Line -(Dx, Dy), vbBlack Picture1.Line -(Ax, Ay), vbBlack Picture1.Line (Hx, Hy)-(Fx, Fy), vbBlue Picture1.Line (Ex, Ey)-(Pxx, Pyy), vbBlue Picture1.Line -(Gx, Gy), vbBlue Picture1.CurrentX = Ax Picture1.CurrentY = Ay Picture1.Print "A" Picture1.CurrentX = Bx Picture1.CurrentY = By Picture1.Print "B" Picture1.CurrentX = Cx Picture1.CurrentY = Cy Picture1.Print "C" Picture1.CurrentX = Dx Picture1.CurrentY = Dy Picture1.Print "D" Picture1.CurrentX = Ex Picture1.CurrentY = Ey Picture1.Print "E" Picture1.CurrentX = Fx Picture1.CurrentY = Fy Picture1.Print "F" Picture1.CurrentX = Gx Picture1.CurrentY = Gy Picture1.Print "G" Picture1.CurrentX = Hx Picture1.CurrentY = Hy Picture1.Print "H" Picture1.CurrentX = Pxx Picture1.CurrentY = Pyy Picture1.Print "P" End Sub Sub Command2_Click() Unload Me End Sub Private Function min2(ByVal x As Double, ByVal y As Double) As Double If x < y Then min2 = x Else min2 = y End If End Function Private Function max2(ByVal x As Double, ByVal y As Double) As Double If x > y Then max2 = x Else max2 = y End If End Function
解答その2.
GRAPESで作図して面積8cm2を求めました.ポイントは,点の座標の計算をすべてダミー点上でやっていることでしょうか.
f(x)=(E.y-H.y)/(E.x-H.x)*(x-I.x)+I.y
P(S.y-R.y)/(R.x-S.x), R.x*P.x+R.y)
Q(5-.5*2*3, Q.x*2/len(H,E), Q.y/3*len(H,E))
Q.x:△PHE, Q.y:PからHEに降ろした垂線の長さ, Q.r:HI
R((F.y-H.y)/(F.x-H.x), R.x*(-H.x)+H.y)
直線HFの係数を表す:y=a*x+b, a=R.x, b=R.y
S((E.y-H.y)/(E.x-H.x), S.x*(-I.x)+I.y)
Iを通り,HEに平行な直線の係数を表す:y=c*x+d, c=S.x, d=S.y
T(-0.71, 6.41)
答を表示する点:四角形PFCG=!{.5*(C.x-F.x)*(G.y-C.y)+.5*len(G,F)*M.r}cm2
A(0, 4)
B(0, 0)
C(6, 0)
D(6, 4)
E(0, 1)
F(4, 0)
G(6, 3)
H(2, 4)
I(2+Q.r, 4)
M((F.y-G.y)/(F.x-G.x), M.x*(-G.x)+G.y, abs(-M.x*P.x+1*P.y-M.y)/Sqrt((-M.x)*(-M.x)+1*1))
直線GFの係数を表す:y=a*x+b, a=M.x, b=M.y
解答その3.
私が一番やってはいけない算数で解きました.
まず問題の条件から,△AEH,△BFE,△CGF,△DHGの面積を求めます.
次に,四角形AEPHの面積が5であることから,△HEPの面積を求めます.
HFによって,この長方形ABCDは二等分されており,△HGFと△FEHは合同なので,台形HFCD,△HGFの面積が求められます.
△HGPと△HEPの面積は等しいので,△PGFの面積が求められます.
故に四角形PFCGの面積は8cm2です.
解答・その5
(ペンネ−ム:小学名探偵)
答え 8平方センチメートル
長方形ABCDの対角にある直角△AEH≡△CGF、
よって四角形EFGHは平行四辺形、
対角線HFは長方形ABCDの中心を通り、それを2等分します。
△EPH=四角形AEPH−△AEH=5−3=2
台形ABFH=長方形ABCD÷2=24÷2=12
△EFH=台形ABFH−(△AEH+△BEF)=12−(3+2)=7
△FGP=△EFP=△EFH−△EPH=7−2=5
四角形PFCG=△FGP+△CGF=5+3=8(平方センチメートル)
解答・その6
(ペンネ−ム:FIVEILAND)
長方形ABCDの面積は6×4=24cm2
次に△EFHと△GHFについてFH=HF、EF=GH(△BFE≡△DHG証明略)、 HE=FG(△AEH≡△CGF証明略)
∴△EFH≡△GHF
これから△EPH=△GHP、△EFP=△GPF
□AEPHの面積は5cm2だから△EPHの面積は5−3=2cm2
△GPF×2=長方形ABCD(24)−△AEH(3)×2−△EPH(2)×2−△DHG(2)×2 △GPF=5cm2
□PFCG=△GPF(5)+△CGF(3)=8cm2
解答 8cm2
解答・その7
(ペンネ−ム:Mr.X)
EGとFHの交点をQと置く。
四角形AEQHの面積と四角形CFQGの面積の和は13
(なぜなら、長方形全体の」面積は24。 長方形から角の4枚の直角三角形を 除いて平行四辺形EFGHができます。 その面積は
24−2×2×3/2−2×1×4/2=14
四角形AEQHの面積と四角形CFQGの面積の和は
2×2×3/2+14/2=13)
HQの延長上にPQ=QRである点Rをとると
四角形AEPHの面積と四角形CFPGの面積の和も
四角形AEQHの面積と四角形CFQGの面積の
それぞれに平行四辺形EPGRの4分の1を削除、
追加したものの和であり、13
従って、四角形CFPGの面積=8
正調で解答!!
解答・その8
(ペンネ−ム:杖のおじさん)
答え 8cm2です
図の点の説明
点Pは対角線HF上の任意のとする。点Qは対角線HFの中間点です。
点Rは対角線EGに対して点Pから垂直に下した点です。
従って∠PRE=∠PRG=90°(直角)です。
□HEFG(平行四辺形)について
対角線HFを引くと△HEFと△HFGは合同で面積が同じです
対角線の中間に点Qがあった場合△EQH=△FQGである。
任意の点Pにした時、△EQP=△GQPの面積が等しいことを証明します。
点Pから対角線EGに垂直に線PRを引く、
底辺はEQ=GQ 高さはPRで同じです、従って面積も同じです
三角形の面積は底辺×高さ÷2なので、両三角形の面積を計算して見ます。
点Pを移動することで△EQPの増減した面積は△FQGに増減しますので
常に△EPH+△FPGは同じです。
△EPH+△FPG=□EFGH/2となります。
面積を計算します
□ABCDの面積=4×6=24cm2
△AHE+△CFG+△EBF+△GDH=(3×2÷2+4×1÷2)×2=10cm2
□EFGH=24−10=14cm2 △HPE+△FPG=14cm2/2=7cm2
△HPE=□AEPH5cm2―△AEH3cm2=2cm2
△FPG=7cm2―2cm2=5cm2
求める□FCGP=△FCG3cm2+△FPG5cm2=8cm2
解答・その9
(ペンネ−ム:巷の夢)
まずE,F,G,Hの四点を結ぶと、△AEH≡△GCF、△EBF≡△GDHよりこの四角形は平行四辺形になります。又、HFは対角線ですから、この線上ならPをどこにとろうが△PEHと△GPFの和は一定、即ちこの平行四辺形の面積の半分となります。ところで、この平行四辺形の面積は長方形ABCDの面積から四つの三角形、△AEH、△GCF、△EBF及び△GDHの面積を加えたものを引いたものになるため、 平行四辺形EFGH=24−(3+3+2+2)=14 となり、この面積の半分ですから7となります。
又、四角形AEPHの面積は5ですから、△EPHの面積は△AEHの面積3を引いた2となります。因って、△FGPの面積は5となり△FCGの面積3を加えた8が四角形PFCGの面積となります。 以上より求めるものは8cm2となります。
解答・その10
(ペンネ−ム:k9)
EF、FG、GH、HEを結ぶと、
△EPH=2cm2
△EFP=5cm2
となる。
EからFHへの垂線の長さとGからFHへの垂線の長さは等しいから、
△GFP=△EFP=5cm2
△GFC=3cm2だから、
四角形PFCGの面積は、8cm2
解答・その11
(ペンネ−ム:mhayashi)
答え:
三角形AEH=3cm2より三角形PEH=2cm2
三角形EBF=2cm2より三角形PEF=5cm2
四角形EFGHは平行四辺形なので三角形PFG=5cm2
三角形CFG=3cm2より四角形PFCG=8cm2
解答・その12
(ペンネ−ム:夜ふかしのつらいおじさん)
答は、8cm2 です。
長方形ABCDの面積は、4×6=24 です。
HFで、この長方形は、合同な2つの台形に分かれます。(台形の面積は12)
元の長方形の角を含む三角形の面積は、簡単に求まります。(3と2)
順にEFGHを結ぶと、平行四辺形になります。(面積は、24−2×(3+2)=14)
平行四辺形は、向かい合う辺の長さが等しいので、△EFHと△GHFは合同です。
(それぞれの面積は、7)
それぞれの三角形の底辺をFHと考えると、面積が等しいので高さも等しくなります。
(高さは、EからFHにおろした垂線、GからFHにおろした垂線)
△EFHを頂点Eと底辺FH上の点Pとを結んで2つに分けるとそれぞれの三角形の面積は底辺の長さに比例します。
△AEPHの面積が5になるためには、△EPHの面積が2であれば良いことになります。
△EFHの面積は7なので、HFを2:5に内分する点がPであれば良いことになります。
△GHFもGPで2つの三角形に分かれますが、面積は底辺の長さに比例します。
△PFCGの面積は、△PFGと△FCGの和なので8となります。
解答・その13
(ペンネ−ム:やんま)
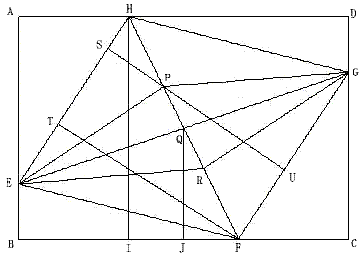
E、Gを結びHFとの交点をQとする。
FH上でFから長さHPと等しい点をRとする。
EとR、GとRを結ぶ。
EとF、FとG、GとHを結ぶ。
HからBCに垂線をおろし、その足をIとする。
QからBCに垂線をおろし、その足をJとする。
PからEHに垂線をおろし、その足をSとする。
FからEHに垂線をおろし、その足をTとする。
PからFGに垂線をおろし、その足をUとする。
他の点は問題と同様。
Sxxx、Sxxxxは添え字を結んだ三角形または四角形の面積とする。
四辺形EFGHとERGPは平行四辺形である。(証明略)
解答1
問題の面積SPFCGはSPFCG=SPFG+SGFC
SGFC =2×3÷2=3(cm2)であるからSPFGの面積が計算できればよい。
SPFG=
題意によりSAEPHは5cm2であり、SGFC=SAEHであるからSEPHは
SEPH = SAEPH −SAEH =5−3=2(cm2)
また
ここでと置き、
この連立方程式を解くと
∴ 四角形PFCGの面積は
SPFCG=SPFG+SGFC=5+3=8(cm2)
答え 8 (cm2)
解答2
問題の面積SPFCGはSPFCG=SPFG+SGFC
SGFC =2×3÷2=3(cm2)であるからSPFGの面積が計算できればよい。
SPFG=
題意によりSAEPHは5cm2であり、SGFC=SAEHであるからSEPHは
SEPH = SAEPH −SAEH =5−3=2(cm2)
またSBFEは2(cm2)でありSABFHはSABFHの半分即ち12(cm2)である。
∴ SEFH = SABFH −SAEH −SBFE =12−3−2=7 (cm2)
∴ 四角形PFCGの面積は SPFCG=SPFG+SGFC=5+3=8(cm2)
答え 8 (cm2)
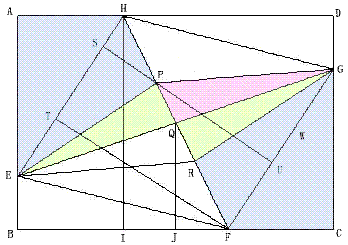
解答3(友人、竹内淳司氏の解)
△PEGと△REGに於いてEQ=GQであるから
SPEQ = SPGQ = SRGQ
Qは重心である。
∴QJ=2 (cm) BJ=3 (cm)
SPEQ =SPEBF −SQEBJ −SQJF
=(12−5)−4.5−1=1.5 (cm2)
∴SPRG = 2SPEQ=3(cm2)
∴SPFCG = SPRG +SCGRF=3+5=8 (cm2)
答え 8 cm2
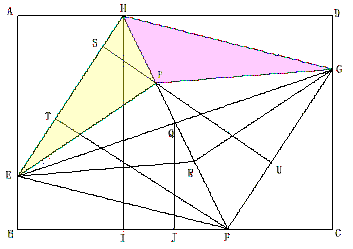
解答4
△HEGに於いてEQ=GQであるから
SHEQ = SHGQ
また△PEGに於いてもEQ=GQであるから
SPEQ = SPGQ
∴SHEP = SHGP
SHEP = SAEPH−SAEH =5−3=2 (cm2)
SDHG = 2 (cm2)
∴SPFCG = SFCDH −SHGP−SDHG=12−2−2=8 (cm2)
答え 8 cm2
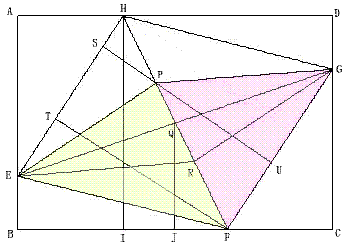
解答5
SPEF=SABFH −SAEPH−SEBF
SABFH=12(cm2)、SAEPH =5 (cm2)、 SEBF =2 (cm2)
∴SPEF=12−5−2=5 (cm2)
EQ=GQ
∴SFEQ=SFGQ、SPEQ=SPGQ
∴SPEF=SPGF
∴SPFCG = SPGF +SCGF=5+3=8 (cm2)
答え 8 cm2
解答・その14
(ペンネ−ム:Toru)
EGを結んでHFとの交点をQとするとEQ=QGよりΔPEQ=ΔPQGだから点PをHF上で移動して も、四角形AEPHの面積と四角形PFCGの面積の和は一定。そこで例えばP=Hとしてこの 和を求めると
(四角形ABCD)×1/2+ΔAEH−ΔHGD=12+3-2=13
よって(四角形PFCG)=13-5=8 答え 8 cm2
解答・その15
(ペンネ−ム:三角定規)
下図のようにEGとHFの交点をOとする。
四角形AEOHは <図1> のように分解できるから, 四角形AEOH=2×2+(2×1)/ 2+(1×3)/ 2=13 / 2
<図2> において EO=GO だから △POE=△POG。
故に,四角形AEPH+四角形PFCG=2×四角形AEOH=13
よって,四角形AEPH=5 のとき,四角形PFCG=13−5=8 [cm2] …[答]
解答・その16
(ペンネ−ム:高橋 道広)
右図のように長方形内に底辺が等しい2つの三角形を作ると、その三角形の面積の和は
1/2×AE×AP+1/2×DG×PD=1/2×AE×AP+1/2×AE×PD=1/2×AE×(AP+PD)=1/2×AE×AD
となります。
この左右の三角形が右図のように等積変形されても面積の合計は変わりません。
さて 今回の問題は PとA,Cを結ぶと 左右の赤い三角形が上に述べた状況に あり上下の青い三角形も同じ状況にあることがわかります。
よって 赤の三角形の面積の和は 1/2×3×6=9
青の三角形の面積の和は 1/2×2×4=4
合計13cm2ですから 求める面積は 9+4-5=8cm2 となります。
解答・その17
(ペンネ−ム:kirkland)
先生 「あたたたっ、頭痛い。昨日は忘年会で飲み過ぎたよ。」
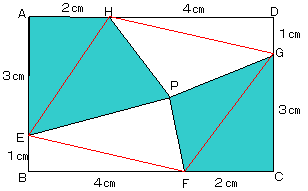
A君 「僕もおとそを飲み過ぎて頭痛いんですよ。」
先生 「何か意味不明だな。12月なのか?1月なのか?」
A君 「冗談に決まってるじゃないですか!図を描きました。」
先生 「何か図が間違ってない?点Pの位置がおかしいのでは」
A君 「そんなの気にしなくてもいいんですよ。描き直すのが 面倒なのでそのままいきましょう。」
先生 「まあいいか。
A君 「E、F、G、Hを結ぶんですよ。 まず、△AEH=△CGF=3cm2です。 それから、四角形EFGHは平行四辺形になります。」
先生 「いいんじゃないかい。」
A君 「で、Pを通ってEHと平行な直線を引いて、等積変形するわけですよ。 つまりPQとEHは平行なので△PEH=△QEHです。 同様に△PFG=△QFGなので、△PEH+△PFG=△QEH+△QFGとなって、 △QEH+△QFGは平行四辺形EFGHの面積の半分ですよね。」
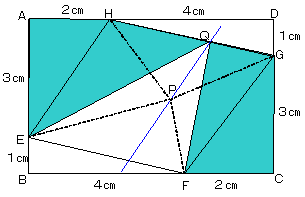
先生 「で、平行四辺形の面積はどうやって求めるの?」
A君 「なめてもらっちゃ困りますねぇ。長方形ABCDから、 四隅の直角三角形を引けばいいだけじゃないですか。
24−2−2−3−3=14だから、
△QEH+△QFG=7cm2です。
あとはまぁ適当にやると、四角形PFCG=8cm2ですか?」
先生 「頭がはたらいてないので、細かい計算ができないけど、 考え方はそんな感じでいいんじゃない。 今晩も忘年会があって忙しいから今日はここまで!」
A君 「またまた、いい加減な話ですねぇ。 頼みますから、来年こそはマジメに教えて下さいよ! では、今月はギャグなしで終わりましょう。」
解答・その18
(ペンネ−ム:佐野允信)
点E,Gから線分HFにおろした垂線の足をそれぞれL,Mとする。
四角形ABFH=四角形FCDH=12(cm2)
△AEH=△FCG=3(cm2)
△EBF=△GDH=2(cm2)
より、
△EFH=△FGH=7(cm2)
よって、
EL=GM
EL=GMより、
△EPH=△HPG
四角形AEPH=5(cm2)、かつ△AEH=3(cm2) より
△EPH=2(cm2)
よって、
△HPG=2(cm2)
四角形FCDH=12(cm2)、かつ△GDH=2(cm2) より
四角形PFCG=12ー2-2=8(cm2) (答)
正解者
夜ふかしのつらいおじさん Toru 杖のおじさん 浜田 明巳 巷の夢 k9 Mr.X 高橋 道広 米ぽん <匿名> FIVEILAND 三角定規 小学名探偵 内海 育 やんま kirkland mhayashi 佐野允信
2004年、最後の問題にもたくさんの解答をお寄せいただきどうもありがとうございました。 補助線として、EFGHをつなぐとこれが平行四辺形になるということを利用した解答が多かったのですが、 それ以外にもいろいろユニークな解法をいただき、感謝しております。 本当にいろいろな解法があるものだと感心いたします。
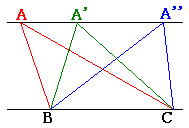
三角形の面積は、
S=(底辺)×(高さ)÷2
で求めることができます。従って、下図のように平行線の一方に三角形の底辺(BC)があり、もう一方の直線上に頂点Aがある場合、点Aが直線上のどこにあっても三角形の面積は等しくなります。あたりまえといえば、あたりまえですが、この性質をうまく使うと今回の問題はあっさり解くことができますね。

 E-mail
E-mail
 top
top