�X�R�D�������`�̖ʐ�
�@���̐}�̂悤�ȁA���a��20cm�A���S�p��144���̂������`������܂��B �_�G�A�I�A�J�A�L�A�N�A�P�A�R�́A�������`�̌ʃC�E�i�Ȑ��̕����C�E�j�� �W��������_�ł��B���̂Ƃ��A�ΐ������̖ʐς̘a�����߂Ȃ����B �������A�~������3.14�Ƃ��܂��B
Weekend Mathematics�^����^���93
�X�R�D�������`�̖ʐ�
�@���̐}�̂悤�ȁA���a��20cm�A���S�p��144���̂������`������܂��B �_�G�A�I�A�J�A�L�A�N�A�P�A�R�́A�������`�̌ʃC�E�i�Ȑ��̕����C�E�j�� �W��������_�ł��B���̂Ƃ��A�ΐ������̖ʐς̘a�����߂Ȃ����B �������A�~������3.14�Ƃ��܂��B
�Z���I�����s�b�N�ɒ���
'00�`'03�N�x��
�Z���I�����s�b�N�ψ����
2001�N��10��Z���I�����s�b�N�g���C�A�����
�E����1
�i�y���l�|���Fteki�j
�����@�Q�T�P.�Q�����Q�@�@�@�i���~�̖ʐς̂Q/�T�j
��@�@���ł�(^^;;
�E����2
�i�y���l�|���FMr.X�j
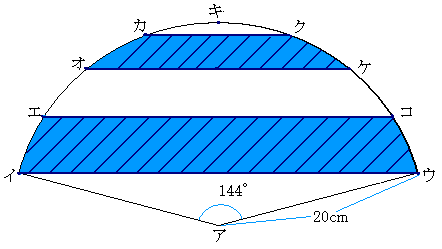
�h�[���i�C�A�L�A�E�j�|�h�[���i�G�A�L�A�R�j�{�h�[���i�I�A�L�A�P�j
�@�@�@�|�h�[���i�J�A�L�A�N�j�� �S�O�O�i144/360-108/360+78/360-36/360�j
�@�@�@�|�Q�O�O�isin144��-sin108��+sin72��-sin36���j�� �W�O�� �� �Q�T�P.�Qcm2
�@�E����3
�i�y���l�|���Fyokodon�j

�m��@�P�n���Z�ȏ�͈̔͂̒m����p�������
�@���a r �A���S�p�Ƃ̋|�`�i��`����A���̉~�ʕ����̗��[�Ɣ��a�Q������ŏo ����Q���ӎO�p�`���������}�`�j�̖ʐς�
�@�@1/2�Er2�E(�� - sin��)
�ŗ^�����܂��i���o�͗e�Ղ��Ǝv���̂ŁA�ȗ����܂��j�B�����p����ƁA���߂�}�`�̖ʐ� S �́A�ȉ��̂悤�ɕ\���ł��܂��i�P�ʁFcm2�j�B
�@�@S �� {1/2�E202�E(2��/5 - sin(2��/5)) - 1/2�E202�E(��/5 - sin(��/5))} + {1/2�E202�E(4��/5 - sin(4��/5)) - 1/2�E202�E(3��/5 - sin(3��/5))}
�@��������A�傫�ȋ|�`�̖ʐς��珬�����|�`�̖ʐς����������̂ł��B�Ƃ���ŁA
�@�@sin(2��/5) �� sin(3��/5) �Asin(��/5) �� sin(4��/5)
�ł�����A�����p����
S �� 1/2�E202�E{(2��/5 - ��/5) + (4��/5 - 3��/5)} �� 202�E��/5 �� 80�� (cm2)�@�E�E�E(��)
�E�E�E�ƂȂ�܂��B���l�v�Z����� S �� 251.2 (cm2) �ł��B
�m��@�Q�n���w���ł��ł������
�@�Ƃ͂����A��@�P�̕��@�ŏo���鏬�w���́Akirkland ����̂Ƃ���̂`�N���܂߁H���������ł��傤�B
�@�l�݂����ȃA�^�}�̕��}�ȑ�l�́A�g����m���𐧌������ƁA�����Ă��܂��܂��B(��
�@�������A��ŎO�p����p���ĎO�p�`�̖ʐς��o���Ă���i�|�`�̖ʐς��o���Ƃ� �ɁA���̍l������p���Ă���j���Ƃɒ��ڂ���ƁA���������܂����������ł��B���� �A�_�A�Ɠ_�L�����Ԑ����Ɛ����J�N�A�����I�P�A�����G�R�A�����C�E�Ƃ̌�_������ �T�A�V�A�X�A�Z�Ƃ���ƁA���́��A�J�T�߁��A�C�Z�A���A�I�V�߁��A�G�X�Ȃǂ����� �����Ă��܂��i���ꂪ�A��@�P�� sin(2��/5) �� sin(3��/5) �Asin(��/5) �� sin(4 ��/5) �ƑΉ����Ă���l�Ɍ����܂��j�B
�@�ȏ��p���āA���߂đ�ӂ̖ʐ� S �����߂鎮�������Ă݂�ƁA�O�p�`�A�J�T�� �ʐς����A�J�T�Ə������Ƃɂ��āA
S �� {(1/2�E202�E2��/5 - ���A�I�P) - (1/2�E202�E��/5 - ���A�J�N)} + {(1/2�E202�E4��/5 - ���A�C�E) - (1/2�E202�E3��/5 - ���A�G�R)}
�E�E�E�ł����A
�@�@���A�I�P�����A�G�R�� 2 �~���A�I�V
�@�@���A�J�N�����A�C�E�� 2 �~���A�J�T
�E�E�E��p���Đ�������ƁA
�@�@S �� 1/2�E202�E{(2��/5 - ��/5) + (4��/5 - 3��/5)}
�E�E�E�ƂȂ�A�ȉ���@�P�ɓ����ł��B
�E����4
�i�y���l�|���Fanik�j
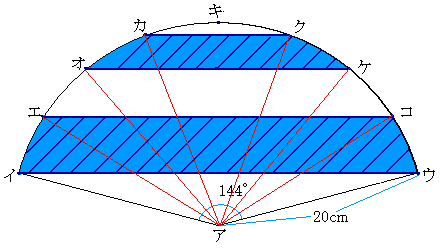
144�x��4��/5
144�x/8��18�x����/10
��`�A�J�N��(1/2)*202*(��/5)��40��
�O�p�`�A�J�N��(1/2)*202*sin(��/5)��200sin(��/5)
��`�A�I�P��(1/2)*202*(2��/5)��80��
�O�p�`�A�I�P��(1/2)*202*sin(2��/5)��200sin(2��/5)
�J�I�P�N �� (��`�A�I�P�|�O�p�`�A�I�P)�|(��`�A�J�N�|�O�p�`�A�J�N) �� (200sin(2��/5)�|80��)�|(200sin(��/5)�|40��) �� 40�|200(sin(2��/5)�|sin(��/5))
��`�A�G�R��(1/2)*202*(3��/5)��120��
�O�p�`�A�G�R��(1/2)*202*sin(3��/5)��200sin(3��/5)
��`�A�C�E��(1/2)*202*(4��/5)��160��
�O�p�`�A�C�E��(1/2)*202*sin(4��/5)��200sin(4��/5)
�G�C�E�R �� (��`�A�C�E�|�O�p�`�A�C�E)�|(��`�A�G�R�|�O�p�`�A�G�R) �� (200sin(6��/5)�|160��)�|(200sin(3��/5)�|120��) �� 40�|200(sin(4��/5)�|sin(3��/5))
����ċ��߂����ʐρ��J�I�P�N�{�G�C�E�R �� 40�|200(sin(2��/5)�|sin(��/5))�{40�|200(sin(4��/5)�|sin(3��/5)) �� 80�|200(sin(2��/5)�|sin(��/5))�|200(sin(4��/5)�|sin(3��/5))
sin(��/5)��sin(4��/5)�Asin(2��/5)��sin(3��/5)����
�� 80�|200(sin(2��/5)�|sin(��/5))�|200(sin(��/5)�|sin(2��/5)) �� 80��80*3.14��251.2
�@�@�`�D251.2cm2
�E����5
�i�y���l�|���F �l�c�@�����j
���W�n������D
�Ƃ���ƁC���߂�ʐςr�́C
�@�@�r���Q{��(�Q�^�T�C�R�^�P�O)�Q�Osin��(�|�Q�Osin��)���Ɓ|��(�^�T�C�^�P�O)�Q�Osin��(�|�Q�Osin��)����}
�@�@�@���W�O�O{��(�R�^�P�O�C�Q�^�T)sin�Q�Ƃ��Ɓ|��(�^�P�O�C�^�T)sin�Q�Ƃ���}
�@�@�@���S�O�O{��(�R�^�P�O�C�Q�^�T)(�P�|cos�Q��)���Ɓ|��(�^�P�O�C�^�T)(�P�|cos�Q��)����}
�@�@�@���Q�O�O{[�Q�Ɓ|sin�Q��](�R�^�P�O�C�Q�^�T)�|[�Q�Ɓ|sin�Q��](�^�P�O�C�^�T)}
�@�@�@���Q�O�O<[�Q(�Q�^�T�|�R�^�P�O)�|{sin(�S�^�T)�|sin(�R�^�T)}]�{[�Q(�^�T�|�^�P�O)�|{sin(�Q�^�T)�|sin(�^�T)}]>
�@�@�@���Q�O�O[{�Q�E�^�P�O�|�Qcos(�V�^�P�O)sin(�^�P�O)}�{{�Q�E�^�P�O�|�Qcos(�R�^�P�O)sin(�^�P�O)}]
�@�@�@���S�O�O{�^�T�|cos(�V�^�P�O)sin(�^�P�O)�|cos(�R�^�P�O)sin(�^�P�O)}
�@�@�@���S�O�O[�^�T�|{cos(�V�^�P�O)�{cos(�R�^�P�O)}sin(�^�P�O)]
�@�@�@���S�O�O[�^�T�|{�|cos(�R�^�P�O)�{cos(�R�^�P�O)}sin(�^�P�O)]
�@�@�@���W�O�icm�Q�j
�@�o�r�D�Z���̖��ɐϕ����g���Ă͂��߂ł��ˁD
�E����6
�i�y���l�|���F�J�̖��j
���E�Ώ̂Ȃ̂ō������ōl����B
�܂��������A�L�ƂS�{�̐������C�E�A�G�R�A�I�P�A�J�N�Ƃ̌�_���e�X�`�C�a�C�b�C�c�Ƃ���B
����Ɛ}�`�A�C�J�c�|���A�C�`�|�}�`�a�G�I�b���ΐ������̖ʐ�
�Ƃ���Ł��A�C�`�߁��J�A�c
�}�`�a�G�I�b���}�`�A�G�I�b�|���A�G�a
�Ƃ���Ł��A�G�a�߁��I�A�b�ł��邩��
�}�`�a�G�I�b����`�A�G�I
�����ċ��߂��`�A�C�I���i�P/�Q�j�~�Q�O�~�Q�O�~�i��/�T�j�ƂȂ�B
���̒l��苁�߂�ΐ����̖ʐς͂Q�{���ĂW�O�A�����A�Q�T�P�D�Q�ƂȂ�B
�E����7
�i�y���l�|���F��̂�������j
�}�P���Q��
�� �J�T�A�Ɓ��A�C�Z�͍����Ȃ̂œ����ʐςł��B
�����̏ؖ�
���J�A�T�ɂ���
�ڃJ�T�A���X�O���@�ڃT�A�J���P�W���@�@�ڃT�J�A���V�Q���J�A�̒������Q�Ocm
���A�C�Z�ɂ���
�ڃA�Z�C���X�O���@�ڃZ�C�A���P�W���@�@�ڃZ�A�C���V�Q�@�A�C�̒������Q�Ocm
���A�Z�\�̖ʐρi�Ԃ̕����@�}�P���Q�Ɓj�����Ƃ���ƁA�����ʐς̎O�p�`���瓯���ʐς̂��������̂� ���A�C�\�Ƒ�`�J�T�\�Z�͓����ʐςł��邱�Ƃ�������܂��B
�܂��A���I�V�A�Ɓ��G�X�A�͍����Ȃ̂œ����ʐςł��B
�����̏ؖ�
���I�V�A�ɂ���
�ڃI�V�A���X�O���@�ڃI�A�V���R�U���@�@�ڃV�I�A���T�S���A�I�̒������Q�Ocm
���G�X�A�ɂ���
�ڃG�X�A���X�O���@�ڃA�G�X���R�U���@�@�ڃG�A�X���T�S���@�A�G�̒������Q�Ocm
���^�X�A�̖ʐρi�Ԃ̕����{���F�̕����@�}�P���Q�Ɓj��y�Ƃ���ƁA�����ʐς̎O�p�`���瓯���ʐς�y�������̂� ���A�G�I�Ƒ�`�I�^�X�V�͓����ʐςł��邱�Ƃ�������܂��B
���@���߂�ʐς�
�}�Q�̖ʐρi�̕����j�͂������`�A�C�J�̂Q�{�̖ʐρi�ʐσC�J�N�E�A�̕����{���F�̕����j ���炨�����`�A�G�I�̂Q�{�̖ʐρi�ʐσI�G�R�P�A���F�̕����j�����������̂ɂȂ�܂��B
�@�@�}�Q�̃C�J�N�E�̖ʐρi�ΐF�̕����{���F�̕����j�����߂܂�
�ʐρ��Q�O�~�Q�O�~�R�D�P�S�~�T�S/�R�U�O�~�Q���R�V�U�D�V�X�X�X�W���R�V�U�D�W
�A�@�������@�Ŏΐ��̖ʐσI�G�R�P�����߂܂�
�ʐρ��Q�O�~�Q�O�~�R�D�P�S�~�P�W/�R�U�O�~�Q���P�Q�T�D�T�X�X�X�X���P�Q�T�D�U
���߂镔���̖ʐς͎��̒ʂ�ł�
�@�\�A���R�V�U�D�W�|�P�Q�T�D�U���Q�T�P�D�Q�@�����Q
�G�N�Z���̃��[�U�[�t�H�[���ł����܂����B���̃t�H�[���ł��B
���̃t�H�[���̍��������̃z�[���[�W�ʼn���������܂��B
�����@�@�@�Q�T�P�D�Q�@�����Q
�E����8
�i�y���l�|���FToru�j
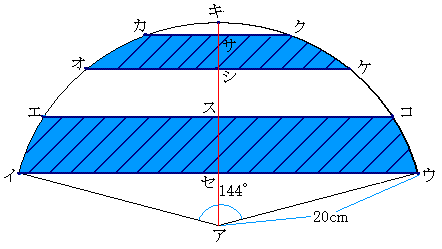
�L�ƃA���Ō���Œ����J�N�A�I�P�A�G�R�A�C�E�Ƃ̌�_�����ɁA�T�A�V�A�X�A �Z�Ƃ���B
�@�ΐ��̂����́i�J�I�P�N�j�̖ʐς́i�J�I�V�T�j�̂Q�{��
�@�@�@�@�i�J�I�V�T�j����`�i�A�I�J�j�{���i�J�A�T�j�\���i�I�A�V�j
�ΐ��̂����́i�G�C�E�R�j�̖ʐς́i�G�C�Z�X�j�̂Q�{��
�@�@�@�@�i�G�C�Z�X�j����`�i�A�C�G�j�{���i�G�A�X�j�\���i�C�A�Z�j
�@�@�@�@��`�i�A�I�J�j�ߐ�`�i�A�C�G�j
�ڃC�A�Z���ڃA�J�T���V�Q���Ȃǂ��烢�i�J�A�T�j�߃��i�A�C�Z�j
�ڃI�A�V���ڃA�G�X���R�U���Ȃǂ��烢�i�I�A�V�j�߃��i�A�G�X�j
����ċ��߂�ʐς�
�@�@�@�@�Qx�i�i�J�I�V�T�j�{�i�G�C�Z�X�j�j���Sx��`�i�A�C�G�j
�@�@�@�@�@�@�@�@��4x20x20x3.14x18/360=251.2
�����@251.2 cm2
�E����9
�i�y���l�|���F�w偂̑���j
�O�p�`�A�C�E�ƎO�p�`�A�J�N�̖ʐς͓������A�O�p�`�A�G�R�ƎO�p�`�A�I�P�̖ʐς��������B �Ȃ��Ȃ�Ɓ�18���Ƃ���i5�Ɓ�90���j���ꂼ��Εӂ̒��������������p�� �Ƥ4�Ƥ5�Ƃ�2�Ƥ3��,5�Ƃ̒��p�O�p�`��ڍ������`������B
�ȉ��A�ʐς̊W���m�F�B�i�O�����`�ƌ��������̂ł��傤���B�ł��`�͈Ⴂ�܂���ˁB�j
�����`�J�L�N����`�A�J�L�N�|�O�p�`�A�J�N����@
�����`�I�L�P����`�A�I�L�P�|�O�p�`�A�I�P����A
�����`�G�L�R����`�A�G�L�R�|�O�p�`�A�G�R����B
�����`�C�L�E����`�A�C�L�E�|�O�p�`�A�C�E����C
���߂�ʐ�S�͇C�|�B�{�A�|�@�ł��邩��
S=��`�A�C�L�E�|��`�A�G�L�R�{��`�A�I�L�P�|��`�A�J�L�N
�@�@�@�@�@�@�@�@�@�@�@�@�|�O�p�`�A�C�E�{�O�p�`�A�G�R�|�O�p�`�A�I�P�{�O�p�`�A�J�N
�`���ɏq�ׂ����R����O�p�`�̖ʐς͏��ł��A �܂���`�̖ʐς͌��ǂ̂Ƃ��뒆�S�p�Ƃ̂��̂�4���B �������S�p72���̐�`�̖ʐςɓ������B
�E����10
�i�y���l�|���F��ӂ����̂炢��������j
���̖��́u�~������3.14�Ƃ���v�Ƃ����̂��q���g�ɂȂ��Ă��܂��B
144�x��8��������ƁA1�̊p��18�x�ɂȂ�܂��B �Ɓ�18���Ƃ���ƁA5�~18����90���Ȃ̂ŁA90���|2�Ɓ�3�Ƃł��B �����ŁA
�@�@sin(90���|2��)��sin(3��)
�@�@cos(2��)��sin(3��)
�@�@1�|2sin2�Ɓ�3sin�Ɓ|4sin3��
�@�@4sin3�Ɓ|2sin3�� �|3sin�Ɓ{1��0
�@�@(sin�Ɓ|1)(4sin2�Ɓ{2sin�Ɓ|1)��0
����������āAsin�Ɓ�(�|1�{��5)�^4
�ȂǂƂ����̂ł́A��5�̈������A�Ɣ�ׂĂ��܂�����܂���B
���ʂɁ�5������Ȃ��̂��ƌ��������܂��B
���āA���~�̒��S�A�ɏW�܂��Ă���p�́A���ׂ�18�x�ł��B�i�}�P�j
�}�P
���̐}�̐F��t���������̖ʐς����ꂻ��A�r1�A�r2�A�r3�A�r4�Ƃ��܂��B
�}�Q�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�R
�@�@�@
�}�S
�}�T
���ꂼ��̖ʐς́A��`���璆�S�A�_�Ƃ���ӎO�p�`�������ċ��߂܂��B
�ӎO�p�`�́A���p�O�p�`�̂Q�{�ł��B
�c���A�L�̉E���ɂ���S�̒��p�O�p�`�ɂ͎��̂悤�ȍ����̊W������܂��B
�@�@���A�N�T �� ���E�A�Z�A
�@�@���A�P�V �� ���R�A�X
�N�T���A�Z�����A�A�T���E�Z�����A�P�V���A�X�����A�A�V���R�X�����Ƃ����A
���S�p��18�x�̐�`�̖ʐς��`�Ƃ����ƁA
�}�U�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�V
�@�@�@
�@�@�@�@�r1��2�`�|���A�J�N��2�`�|2���A�N�T��2�`�|����
�@�@�@�@�r2��4�`�|���A�I�P��4�`�|2���A�P�V��4�`�|����
�@�@�@�@�r3��6�`�|���A�G�R��6�`�|2���A�R�X��6�`�|����
�@�@�@�@�r4��8�`�|���A�C�E��8�`�|2���A�E�Z��8�`�|����
���߂�ʐς��r�Ƃ���ƁA
�r ���i�r2�|�r1�j�{�i�r4�|�r3�j ���i�i4�`�|�����j�|�i2�`�|�����j�j�{�i�i8�`�|�����j�|�i6�`�|�����j�j ���i2�`�|�����{�����j�{�i2�`�|�����{�����j ��4�`
�܂�A���S�p 4�~18�x��72�x �̐�`�̖ʐςƈ�v���܂��B
�r ���i��2�j�~�i4�^20�j ���i1�^5�j�~�i��2�j�@�@�@�i��3.14�A����20�����j ��251.2�icm2�j
�E����11
�i�y���l�|���F�O�p��K�j
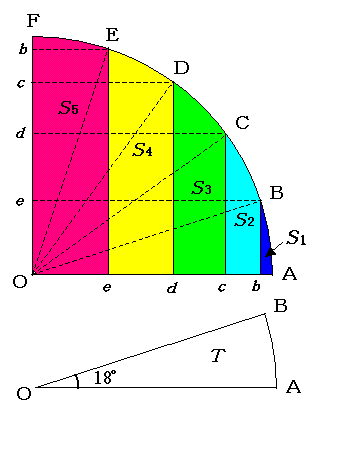
�@����ł����C�E�}�ōl�@���܂��B
�@B�CC�CD�CE�́C4���~��AF��5�����_�ł��B
�@�}�̂悤�ɐF�������������̖ʐς�S1�C�`�CS5�C���S �p18���̐�`�̖ʐς�T�Ƃ���ƁC
�@�^����ꂽ���肪���߂�ʐς͂����2�{��
�@�@�@�@20�~20�~3.14�~4/20��251.2 [cm2] �c�m���n
�E����12
�i�y���l�|���Fkirkland�j
�`�N �u��C�ɂ����܂����I
��`�A�I�J�{���A�J�N�{��`�A�N�P�|���A�I�P�{��`�A�C�G�{���A�G�R�{��`�A�E�R�|���A�C�E
�Ȃ̂ł����A���A�J�N�����A�C�E�A���A�G�R�����A�I�P�Ȃ̂ŁA
���ǁA��`�A�I�J�{��`�A�N�P�{��`�A�C�G�{��`�A�E�R
�Ƃ������ƂŁA�S�̂̔����ł����ƁA�����`�I�ȏ�I�v
�搶 �u���炭�G���ˁB����Ȃ�A�Ƃ��ĔF�߂��B�v �`�N �u�܂��A����ȕ��ʂ̉́A�E�H�[�~���O�A�b�v�Ƃ������ƂŁB ���͂ˁA������̉��������J�b�R������ł���I�v �搶 �u�Ӗ����Ȃ����C���ˁ`�v �`�N �u���������̎Z���I�����s�b�N�Ȃ���A�撣���Ă݂܂�����B �S�N��́A�l�͍��Z���Ȃ̂ŁA�o��ł��܂���ˁB�v �搶 �u�Z���I�����s�b�N���Ă����̂́A���N�����Ȃ��́B ����Ɏc�O�Ȃ���A�S�N����N�͏��w�U�N���̂܂܂��Ǝv�����B�v �`�N �u�c�c�B�v �搶 �u���āA�J�b�R�����̂��n�߂Ă݂Ȃ�����B�v �`�N �u��������[�I�}��`���̂��ʓ|�Ȃ̂ŁA�����������ōl���܂��ˁB�܂��A�Ԃ̎O�p�`��̎O�p�`�̕����Ɉړ����� �܂��B�i���}�j���́A�ړ��ł��邩���āH�ǂ����90���A36���A54���̒��p�O�p�`�����A�Εӂ̒������ǂ���� ��`�̔��a������Ł`���I�v
�搶 �u�ق��ق��v �`�N �u���ɂ܂��A�Ԃ̎O�p�`��̎O�p�`�̕����Ɉړ������܂��B�i���}�j���̂Ƃ��A���F�̕����͂Q��d�Ȃ��Ă��邱�Ƃɒ��ӂ��܂��傤�I�v
�搶 �u�ق��ق��v �`�N �u����ł����āA�܂��܂��A�Ԃ��O�p�`����O�p�`�̕����Ɉڂ��ƁA�ف`��A���܂��������ł��傤�I�v
�搶 �u���́A�ړ��ł���́H�v �`�N �u�P��ڂ̈ړ�����l����ƁA�s���N�̕����̒����͂ǂ���������Ȃ�ł��ˁ`�B ������A�ԂƐ̎O�p�`�͍����Ȃ�ł���B�v �搶 �u�Ӂ`��A�Ȃ�قǁB�Ƃ���ŁA�����̓{�P�܂���\�肶��Ȃ������́H�v �`�N �u���̂��肾������ł����ǂˁA�}��`���̂ɔ�ꂿ����āA�M���O���l����ɂ��Ȃ�������ł���`�B TV���ςȂ��Ⴂ���Ȃ��̂ŁA�Ƃ��ƂƋA��܁[���B�ł́A���悤�Ȃ�`�v �搶 �u���`���I���`���I ���`�s����������B���ς�炸�������傱���傢�ȓz���ˁ`�B�̐S�̓������o�����ɋA�����������B�v
������
Mr.X Toru �l�c�@���� teki ��ӂ����̂炢�������� ��̂������� yokodon �O�p��K �J�̖� �w偂̑��� anik kirkland
���̂悤�Ȑ}�`�̖��ɉ���̂́A��ςł���ˁB�C���X�g��Y���ĉ��������������� �����A�ǂ������肪�Ƃ��������܂����A���ӂ������܂��B
���̖����l����Ƃ��A���S�p18���̐�`���▭���Ǝ��͊����܂����B �~����̓_�ƒ��S�Ƃ�����ł����ƁA18���̐�`������A����Ɠ����ɍ����ȎO�p�`�����g���p�������܂��B ��������܂��g���Ɠ����͂������肵���`�ɂȂ�܂��B �O�p��K�����̉́A�X�ɍ��W�����邱�ƂŁA �X�ɂ�������킩��₷�����̂ɂȂ��Ă���Ǝv���܂��A���S�������܂����B

 E-mail
E-mail
 �߂�
�߂�
 top
top