Weekend Mathematics／問題／問題91

９１．長針と短針の問題

B君が本を読み始めたとき、時計の針は午後９時５５分から午後１０時の間を指していました。２時間たらずで本を読み終えたとき、 長針と短針の位置が読み始めたときとちょうど入れ替わっていたとします。

1. 本を読んでいる間に短針が回転した角度と、長針が回転した角度を合計すると何度ですか？
   
   
2. 本を読んでいる間に短針が回転した角度は何度ですか。
   
   
3. １１時５９分のとき、長針と短針の間の角度は何度ですか。
   
   
4. 本を読み終えた時刻は、午後１１時何分ですか。
   
   

解答・その1

（ペンネ−ム：巷の夢）

(1) 元々の長針と短針が作る狭い方の角度をαとすると、約2時間経過後、 長針と短針が反対になっていたので、これらの移動角度の和は720°である。

(2) 短針の移動角度をX°とすると長針のそれは12X°であるから
13 X°＝720°が成立し、X＝720°/13　となる。

(3) 11時59分は11時から59分後であるから、長針は354°動き、短針はその1/12動くので354°/12となる。 元々の短針は330°動いているから二つの針が形成する角度は354°/12　−24°＝11°/2　となる。

解答・その2

（ペンネ−ム：杖のおじさん）

答え

１．720°です。
２．55.38°
３．１１時５９分の時の長針と短針の間の角度は５．５°です。
４．１１時49分５５秒８です

計算

１．長針と短針の角度をｘ°とすると、長針の回転は360°*2―x°で、 短針の回転角度はx°なので合計すると720°になります。

２．短針の動いた角度は合計の1/13なので720/13となります。

３．１１時５９分のとき、長針と短針の間の角度は何度ですか。
長針の位置は30/5=6°短針の位置は30/60=0..5
従って　　　６°−０．５°＝５．５°です。

４．短針の動いた角度は720/13=55.38°である。
これを分で計算720/13/5.5=1440/143分
これを計算して　１１時６０分−10*10/143=１１時49*133/143分になります
60-1440/143=7140/143=49+133/143=49+55.8（秒）
計算すると１１時４９秒５５秒８になります。秒以下四捨五入しました。

解答・その3

（ペンネ−ム：teki）

（１）　７２０度
（２）　７２０/１３度
（３）　5.5（１１/２）度
（４）　１１時５０分（正確には１１時7140/143分）

（１）は長針と短針のなす角が始めと終わりで同じなのですから、あわせて360×２ 度回ったことになります。

（２）は、長針の回る速さ（角速度）は短針の回る速さの1/12ですので、あわせて 720度を12：1に分ければいいんですね。

（３）は、１分間に長針は360/60＝６度、短針は30/60＝0.5度回るので、その差は 5.5度となります。

（４）が、ややこしかったです。

解答・その4

（ペンネ−ム：三角定規）

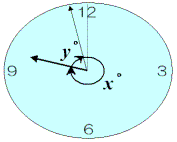
(1) 右図のように長針の回転角を xﾟ，短針の回転角を yﾟ とすると， 明らかに，x＋y＝720ﾟ

(2) 時計の性質より x＝12 y だから

　　　　　

(3) 11時59分のとき
　　　長針と12時の間の鋭角は，360ﾟ÷60＝6ﾟ
　　　短針と12時の間の鋭角は， 30ﾟ÷60＝0.5ﾟ
　　　　　　　　よって， 5.5ﾟ

(4) (3)より，11時m分のときの長短針のなす角は330ﾟ−5.5mﾟ だから
これに(2)の結果を代入して，本を読み終えた時刻は

　　　　　　　　　　　　　　11時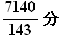

※　分母子に17までの素数がすべて現れているのは，偶然ですよね ??

解答・その5

（ペンネ−ム：Toru）

1. 720度

2. 長針は短針の１２倍の速さで回るから、これと１.とから720/13度

3. １２時では針が重なっており、１分戻すと、短針は30/60=1/2（度）長針 は360/60=6（度）戻るから、6-1/2=11/2 （度）

4. １２時から１分もどるごとに短針と長針は11/2度はなれるので、720/13度はなれ るには、(720/13)/(11/2)=1440/143（分）もどせばよい。 60-1440/143=7140/143 （分）≒49'55"8
すなわちほぼ１１時５０分（１１時４９分５６秒）

解答・その6

（ペンネ−ム：Mr.X）

９時Ｘ分から１１時Y分
6X=330+Y/2 , 6Y=270+X/2

１．の答え・・・７２０度

２．の答え・・・６（Ｘ−Ｙ）＝７２０度/１３

３．の答え・・・３３０＋５９/２−６×５９＝５．５度

４．の答え・・・Ｙ＝１１９×１２０/（２×１１×１３）
従って、１１時７１４０分/１４３

解答・その7

（ペンネ−ム：寺脇犬）

１、短針→長針の位置に、長針→一周して短針の位置に。
ってことは　　長針の移動した角度に短針の移動した角度を足すと
めでたく長針は　２周したことになるので　　　答えは　　　７２０度

２、長針は６０分で　３６０度　　短針は60分で　３０度と言う一定の速度で移動している。
長短２針足して７２０度移動した場合でも　この比、つまり１２対１の割合で移動したわけやから
　　　　短針は　　　720度　×　1/13 =55と5/13 度 回転した。

３、11時００分のとき、　短針は長針より　３３０度進んでいると考えると
11時59分のときの２針の隔たりは
　　　　３３０度ー　５．５度×５９＝　５．５度です

４、読み終わった時点での　２針の隔たりは　５５と5/13度
この後２針の隔たりが無くなって重なるのは　12時００分だから
　　　　５５と5/13 ÷　　５．５　　＝　　1440/143
読み終わった時点から　　1440/143後である
てなわけで、
　　　　６０−　1440/143　=7140/143
7140/143は　４９と133/143だから
　 　　　　求める答えは　11時49と133/143分

解答・その8

（ペンネ−ム：蜘蛛の巣城）

時計の長針と短針の動きをとらえるためには、角速度が手がかりになります。 設問文からみて単位は「度数（角）と分（時間）」を使用します。
長短針の角速度はそれぞれ　6度/分　と　(1/2)度/分　です。 これはスピードの比が12:1であることを示しています。

１.針の回転を目で追って即答。2回転、720度

２．スピード比で比例配分して短針分は (720/13) 度

３．あと1分で12時。角速度から1分間の回転角 6度 と (1/2)度 の差をとって (11/2)度

４．前問の結果が１分あたりに生ずる長短針の差です。
設問２．の角度を解消して12時になるのに何分かかるか。
２．の結果を３．の結果で割ると (1440/143)分。
即ち、12時(1440/143)分前
即ち、11時(7140/143)分

解答・その9

（ペンネ−ム：夜ふかしのつらいおじさん）

長針も短針も時計回りに動きます。
角度を測る基準を12時の針の位置とし、時計回りを正とします。
始めの時刻 Ｔ_n に長針の方が進んだ位置にあったとします。 （見た目の角が長針の方が大きい）
長針の進む速さは　6［度／分］、短針の進む速さは　1／2［度／分］です。
長針が始めに短針のあった位置に、短針が始めに長針のあった位置に来ることを考え ます。
始めからの経過時間をｔ［分］とします。
すると、長針と短針とが入れ替わったことになるので、

　　　6ｔ＋　(1／2)ｔ　＝　360×ｎ［度］

　　　ｔ　＝　(720／13)×ｎ［分］

（つまり、始めの時刻Ｔ_nから(720／13)×ｎ［分］後に長針と短針の位置が入れ替わります。 720／13［分］は約55分23秒です）
そのとき短針が動く角度は、(1／2)×(720／13)×ｎ＝(360／13)×ｎ［度］です。
（360／13［度］は約27.7［度］です）
さて、23時59分は、24時からそれぞれの針が、負の方向に1［分］進んだと考えられ ます。
だから、長針と短針の間の角度は、（−6）−（−1／2）＝−11／2［度］です。
これは、長針と短針のなす角が１位ごとに −11／2 ［度］ずつ増えていくことを意 味しています。
だから、（(360／13)×ｎ）÷（−11／2）＝−(720／143)×ｎ ［分］で、
24時から何分さかのぼれば、時刻 Ｔ_n になるかがわかります。
（720／143［分］は約5分と2.1秒です）

ｎ	24:00からさか のぼる時間［分］ (720／143)×ｎ	その時刻	さらにさか のぼる時間［分］ (720／13)×ｎ	その時刻 （ 始めの時刻） Ｔn	短針と長針の 間の角度 (360／13)×ｎ
1	5.03	23時54分57.9秒	55.38	22時59分34.8秒	27.69
2	10.07	23時49分55.8秒	110.77	21時59分09.7秒	55.38
3	15.10	23時44分53.7秒	166.15	20時58分44.5秒	83.08
4	20.14	23時39分51.6秒	221.54	19時58分19.3秒	110.77
5	25.17	23時34分49.5秒	276.92	18時57分54.1秒	138.46
6	30.21	23時29分47.4秒	332.31	17時57分29.0秒	166.15
7	35.24	23時24分45.3秒	387.69	16時57分03.8秒	193.85
8	40.28	23時19分43.2秒	443.08	15時56分38.6秒	221.54
9	45.31	23時14分41.1秒	498.46	14時56分13.4秒	249.23
10	50.35	23時09分39.0秒	553.85	13時55分48.3秒	276.92
11	55.38	23時04分36.9秒	609.23	12時55分23.1秒	304.62
12	60.42	22時59分34.8秒	664.62	11時54分57.9秒	332.31
13	65.45	22時54分32.7秒	720.00	10時54分32.7秒	360.00

この問題は、ｎ＝2 の場合ですから、

１．は720度

２．は55.38度

３．は5.5度

４．は23時49分55.8秒です。

解答・その10

（ペンネ−ム：kirkland）

Ａ君 まず、読み始めたときの長針の位置（読み終わったときの短針の位置）をア、 読み終わったときの長針の位置（読み始めたときの短針の位置）をイとします。 すると、長針の動いた角度（赤線）と短針の動いた角度（青線）の和は、 ちょうど２周分で720度です。（右図）はははっ、楽勝、楽勝！ 先生 順調ではないか。で、（２）は？ Ａ君 長針は１時間(60分)で一周しますから、１分間に360÷60＝６度進みます。 短針は12時間(720分)で一周しますから、１分間に360÷720＝0.5度進みます。 というわけで、同じ時間に長針と短針の進む角度の比は、６：0.5＝12：１です。 (１) で、長針と短針の進んだ角度の和が720度と分かっているので、短針が進んだ角度は、 720× ＝55 度です。 簡単、簡単。調子に乗って一気に(４)を出しちゃいますよ！ 短針が55 度進めばいいんだから、 本を読んでいた時間は、55 ÷0.5＝110 分間ですな。 というわけで……えっっ！？こんなのを求めても意味ないですねぇ〜。 先生 調子に乗っちゃぁイカン。ちゃんと(３)からやりなさい。 Ａ君 はぁ。11時59分っていうことは、12時の１分前ですね。12時では、長針と短針は重なってますよね。 11時59分では、重なっている状態から長針が６度戻って、短針が0.5度戻っているので、両針は5.5度 離れています。 先生 そうそう。で、(４)は？ Ａ君 読み終わったときには両針の間は55 度離れています。 12時から１分さかのぼるについて、両針の間は5.5度 ずつ離れていくので、読み終わったのは12時の55 ÷5.5＝ 10 分前です。ということで、読み終わった時刻 は、午後11時49 分で〜す。 先生 正解だね。 Ａ君 ところでこのＢ君っていうのは、変人ですか？まともな人間が、49 分なんて時刻を時計から読みとれる訳ないで すよ！ 先生 うん、君の言う通り、この問題の登場人物はそうとうの変人だね。細かすぎるというか、つまらないことにこだわり すぎるというか、単なる大バカモノというか……。その上、口やかましいし、何かと無礼だし……。 Ａ君 あれ？珍しく僕の過激発言（掲載されないことが多いのですが）に同調してくれましたね。 てっきり怒られると思ったのに。それにしても、『口やかましい』とか『無礼だ』って？ 先生 東大寺学園のオリジナルの問題に登場するのは『Ｂ君』ではなく『Ａ君』なんだよ！ Ａ君 ……。

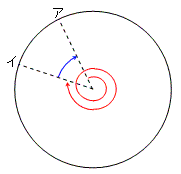
解答・その8

（ペンネ−ム：午年のうりぼう）

正解者

Toru	巷の夢	teki
夜ふかしのつらいおじさん	杖のおじさん	Mr.X
kirkland	蜘蛛の巣城	三角定規
寺脇犬	午年のうりぼう

皆さん、夏休みを迎えられているのでしょうか？　 いただいた解答の数が少ないので、ちょっと寂しい思いがしています。 今回は時計の針の問題ですが、時計の針の規則的な動きを考えるのは、 なかなかおもしろいですね。
この問題は、(4)の問題を解くために、絶妙に(1)〜(3)で準備がされています。 何人かの方が指摘してくださっているように、(3)の結果が１分間における長針と短針の回転の差です。 (2)の結果をこれで割れば、ちょうど重なる１２時からどれだけさかのぼればいいかがわかるわけです。 こうして考えることで、方程式を使わずして解くことができます。

E-mail 戻る top