Weekend Mathematics／問題／問題90

９０．ハノイの塔

バラモン教のある寺院に、次のような伝説があった。

「この寺院の中に３本の大理石の柱がある。その１本Ａに、すべて大きさの違う ６４枚の黄金の円盤が、大きいものから順に刺してある。これを１回に１枚ずつ動かし、 全部を別の柱Ｂに移し終えたとき、この世は終わる」

というものである。
１枚を動かすのに１秒かかるとすると、この世が終わるのはいつか？ ただし、移動するとき、小さい円盤はつねに大きい円盤の上になければならない。 そのためには、もう１本の柱Ｃを補助柱として使ってよい。

解答・その1

（ペンネ−ム：杖のおじさん）

答え
５８４５億４１７７万１８６４年１４時間２０分１５秒後にこの世は終わります。
計算式は２^６４−１ですが
エクセルのヘルプにも書いてありますが、エクセルの仕様では数値は「１５桁の有効数字まで」 とのことなので数値が１５桁以上になると１０^{（N桁―１５桁）}未満が丸められて ２^６４の計算が１位まで出来ません、従って次のようにいたしました。

２^６４−１＝２^３２＊２^３２−１
２^３２=4294967296
4294967296×4294967296−１

２^６４−１の計算を次の通りエクセルのセルの文字列結合を利用して行いました。

２^６４−１＝18446744073709551615秒
Aは６４枚を移動完了に要する秒数
A=18446744073709551615秒
Bは一年の秒数
６０＊６０＊２４＊３６５＝３１５３６０００秒
B=31536000秒
Cは年数
C=A/B
C=18446744073709551615/31536000=584942417355年
584942417355*31536000=18446744073709500000……・D
A- D＝５１６１５秒余り、　これを時間に換算すると１４時間２０分１５秒になります。
うるう年の計算（４年に一度、一年の日が一日多くなります。）
C/4＝146235604339年…・146235604339日　…・・E

年に換算します。
E/365=400645491年…・F　　になりますので、先に計算した年数から引きます。
C−F=584541771864年
ちなみに地球の誕生は４６億年前と言われています。

解答・その2

（ペンネ−ム：anik）

１枚の時・・・１回
２枚の時・・・３回
３枚の時・・・７回
４枚の時・・・１５回
…………………………
ｎ枚の時・・・２^ｎ−１

６４枚の時・・・２^６４−１＝18446744073709551615

18446744073709551615秒（約五千八百億年）

この問題は中学校の時がんばって解きましたね。
2⁶⁴を求めるのに
2¹⁶＝65536
65536²＝4294967296
4294967296²＝(42949＋67296)²
　　　　　　　 ＝42949²＋2×42949×67296＋67296²
　　　　　　　 ＝18446744073709551616
と2,4,8,16,32,64．．．と2倍していく方法と二種類やって確かめたものです。大変でしたね。
楽に求める方法はあるんですか。

解答・その3

（ペンネ−ム：kirkland）

Ａ君 早速ですが、ヒントを下さい。 先生 何を急いでるんだ？ Ａ君 だって、早くしないとこの世が滅んでしまいますよ！ こんな問題はさっさと片づけて、残された時間を存分に楽しまなきゃ！ ゲームもしないといけないし、マンガも読みたいし…、とにかく時間が ないんですよ！最後の晩餐は何にしようか？お寿司も食べたいし、 ハンバーグもカレーも食べたいし、お菓子だけっていうのもいいなあ〜。 先生 ……。まぁ、例によって、簡単なところで実験してみれば？ Ａ君 円盤が１枚のときは１秒後、円盤が２枚のときは、３秒後ですね。（右表） 先生 では、円盤が３枚のときは？ちょっと頭を使って考えてみなさい。 Ａ君 円盤３(以下、単に３)をＢに動かす為には、１，２がＣにないといけません。 １， ２をＡからＣに移動させるのは、さきほどと同様に３秒かかります。 そして、４秒後に３をＢに動かします。Ｃにある１，２をＢに移動させる のにまたまた３秒かかるので、合計で７秒かかります。（右表） 先生 そんなんでいいんじゃないかい。円盤が４枚のときもすぐに出せるだろ。 Ａ君 楽勝ですな！１〜３をＣに移動させるのに７秒、４をＢに移動させるのに １秒、１〜３をＢに移動させるのに７秒で、合計７×２＋１＝15秒です！ 先生 そうそう。円盤５枚だと、15×２＋１＝31秒だね。 Ａ君 ２倍して１を足すっていうのをどんどん計算していけばいいわけですね。 先生 面倒くさくないかい？数字に並びに着目しなさい。 Ａ君 １，３，７，15，31，63，127，……？？？ 何ですか、この数字の並びは？ うーん、焦るなあ！早くしないと、この世が滅んでしまう〜！ 先生 それぞれに１足してみなさい 先生 はぁ、２，４，８，16，32，64，128，…。 分かりましたよ、ちょうど２倍ずつになっていますね！ １，３，７，15，31，63，127，……っていうのは、 ２−１、２２−１、２３−１、２４−１、２５−１、２６−１、……ですね！ Ａ君 インチキ臭いけど、まぁそんなんでいいんじゃないの。 先生 円盤が64枚のときは、２64−１秒後です。 Ａ君 正解！ 先生 でもこれって、どれぐらいの大きさなのか見当も付きませんね。というわけで、電卓で計算すると、 18446744073709551615秒後。っていうことは、18446744073709551615÷60÷60÷24÷365≒584942417355年後っ！ なあんだ、当分の間は大丈夫なんですね。では、さっそく余裕をかまして遊びに行ってきま〜す！

円盤２枚 Ａ Ｂ Ｃ スタート １ ２ 　 　 １秒後 　 ２ 　 　 １ ２秒後 　 　 ２ 　 １ ３秒後 　 １ ２ 　 円盤３枚 Ａ Ｂ Ｃ スタート １ ２ ３ 　 　 １秒後 　 ３ 　 １ ２ ２秒後 　 　 ３ １ ２ ３秒後 　 １ ２ ３

解答・その4

（ペンネ−ム：蜘蛛の巣城）

「円盤が刺してある」という表現から想像されたのは、 柱Ａから任意の円盤を抜き取り柱Ｂの所定の位置に差し込む図でした。 これなら64秒でこの世は終わります。現在、円盤の移動作業中なのでしょうが、 どう考えてもこの世は65秒以上続いています。 文意をとるのに苦しみましたが、以下のように問題を解釈し直して解答します。

　　

「３つのサークルＡ，Ｂ，ＣがあってサークルＡ内にすべて大きさの異なる 皿がピラミッド型に積み重ねてある。この皿の塔をそっくりサークルＢに 移す。皿は1枚ずつ3つのサークル間だけを移動し皿の大小の順序を逆転 させてはならない。完成に何手かかるか。」

初期状態P₀から第１手はサークルＢかＣへ最小の皿を移す。 これが状態P₁である。第2手は空のサークルに2番目に小さい皿を移し、 3手目に最小の皿を2番目の皿の上に移す。状態P₂である。 4手目に3番目に小さい皿を空のサークルに移動する事ができる。 皿の大小の順序は逆転させてはならないから、 上の手順のように空のサークルを用意して新しい皿をＡ塔の１番上から移動するのである。 さて、次の定義を設ければ直ちに次の推定ができるであろう。

定義「サークルＢかＣに、上より順に最小の皿１から皿ｎまでが 重なってあり、Ａ塔は上より順に皿ｎ＋１以下が重なって いる状態をP_nという」

推定「状態P_nから状態P_n+1へ移行するのに2ⁿ 手かかる」

この推定はｎ＝0､1､2､3､4程度の実際例で確認される。 また一般には、上の推定をそのまま仮定とし、次の命題を証明すればよい。

命題「状態P_n+1から状態P_n+2へ移行するのに2ⁿ⁺¹手かかる」

以下、証明。 Ａ塔の上から皿ｎ＋２を空サークルに移すのを第1手として、 他の塔の1番下の皿を残して皿ｎ以上をＡ塔の上に移す。これは移動場所などの相違はあるものの、 仮定した手順に準ずるとみなしてよい。 次に、皿ｎ＋１を皿ｎ＋２の上に移すのを第1手としてＡ塔の皿ｎ以上を皿ｎ＋１の上に移す。 これも仮定の手順に準ずる。手数の合計は

　　　　２ⁿ＋２ⁿ＝２ⁿ⁺¹

結論。初期状態から状態P_nを完成するのに要する手数は

　　　　１＋２＋２²＋・・・＋２^nｰ1＝２ⁿ-1

従って、64枚の皿の塔を移動させるのに、次の手数を必要とする。

　　　　２⁶⁴−１手

1手１秒で何年かかるか。この世の終わらぬ理由がわかりました。
尚、64枚の皿でＢ塔をつくるためには第1手をサークルＣに施さなければなりません。 また、上記の解答が最短の手数であることは、 実際例での確認と一般の証明の中に盛り込むことが出来ます。

解答・その5

（ペンネ−ム：aa）

こういうのは数を少なくして実際にやってみよー、が基本ですね。

1)黄金の円盤が1枚の場合
　これは明らかにA->Bの１回

2)黄金の円盤が2枚の場合
　　この場合は、
　　　A->C
　　　A->B
　　　C->B
　　の3回

3)黄金の円盤が3枚の場合
　　この場合は、
　　　A->B
　　　A->C
　　　B->C
　　　A->B
　　　C->A
　　　C->B
　　　A->B
　の7回。

4)黄金の円盤が4枚の場合
　　そろそろ何か考えないと、面倒になってくる。
　　一番下の大きな円盤を動かすためには、その上の3枚をCに移しておく必要がある。
　　3)よりこれには7回掛かる。
　　次に、一番大きな円盤をBに移し（1回)、Cの3枚をBに移すのに7回必要。
　　よって7+1+7=15回

5)黄金の円盤が5枚の場合
　　15+1+15=31回

6)黄金の円盤が6枚の場合
　　31+1+31=63回

ふー、この調子で64まで行けばいいのだが、64は遠い(!)ので、いままでの回数を振り返ってみると、

　　1,3,7,15,63

う〜ん、これは2ⁿ-1って形じゃん。

7)ちなみに黄金の円盤が7枚の場合
　　63+1+63=127・・・おー、まさに2⁷-1だぁ。

よって64枚の場合は、2⁶⁴-1回必要。

Windowsの関数電卓でこの値を求めると、

　2⁶⁴-1=18446744073709551615

というととてつもなく大きな値。

1年は、60*60*24*365=31536000秒なので、これで割って、 およそ584942417355。 5850億年かかるというもの。

解答・その6

（ペンネ−ム：teki）

今月は、超有名な「ハノイの塔」ですか。
最短手数は、円盤の枚数が、２枚の時３手、３枚で７手、４枚で１５手・・・で、ｎ 枚では２^ｎ-１手になります。

円盤の枚数が１枚のときは、明らかに１手です。 これに１枚加われば、どうなるでしょう？
上の小さな円盤を移すのに１手、２枚目の円盤を移すのに１手、最初の円盤を積み上 げるのに１手の合計３手かかります。
次に、もう１枚加われば、２枚のときの状態にするのに３手、それを戻すのに３手、 残った１枚を移すのに１手の合計７手です。
同様にｎ枚の円盤を移すのに要する手数は、ｎ-1枚の時に必要な手数×２+１手とな ります。
つまり、ｎ枚のときの手数をＨ（ｎ）とすると、

　　　Ｈ（ｎ）＝２×Ｈ（ｎ-1）+１　

という漸化式が成立します。これを変形すると、

　　　Ｈ（ｎ）+１＝２×（Ｈ（ｎ-1）+1）　

となります。 つまり、Ｈ（ｎ）+１は初項２、公比２の等比数列ですので、その一般項は、２^ｎです。 よって、Ｈ（ｎ）＝２^ｎ-１が成立することになります。

で、６４枚では、２^６４-１手ですから、18,446,744,073,709,551,615手、１手１ 秒ですから、約584,942,417,355年 かかることになります。（なんと、５８００億年以上かかっちゃうんですね。） 地球が誕生してから約５０億年ですので、この世の終わりは「当分こない」ってこと になりますね。 もっとも、昨今のコンピュータの発達によって、１手が10^-10秒くらいでできるよ うになれば、あと６０年ほどで終わっちゃいますけど・・・。（それまで、私は生きてないって）

解答・その7

（ペンネ−ム：巷の夢）

一般的にN個の円盤を移し換えるための最小回数をM_ｎとすると、 M_１は明らかに１である。 ここでN＞１とし、N個目の一番大きな円盤を２本目の大理石の柱に移動するためにはN−1個の円盤を ３本目の大理石の柱に移動しておく必要がある。 即ち、M_ｎ−１回移動する必要がある。 この作業が完了後、最大のN番目の円盤を２本目の大理石の柱に移動するには１回の移し換えが必要。 ここまで完了したら３本目の大理石の柱にあるN−1個の円盤を２本目の大理石の柱に移動すればよく、 この回数はM_ｎ−１であるから、

　　　M_ｎ＝２M_ｎ−１＋１

が成立する。この漸化式を解いて、

　　　M_ｎ＝２^ｎ−１

となる。
ここでｎ＝64を代入すると、２^６４−１≒　5.849×10^１１　年となる。

解答・その8

（ペンネ−ム：Toru）

N枚の円盤を移すのにF(N)秒かかるとする。（N＋１）枚移すには、条件よりまずN枚 を柱C移して、一番大きな円盤を柱Bへ移し、その後柱CのN枚を柱Bへ移すことになる から、

　　　F（N＋１）＝F（N）＋１＋F（N）＝２F（N）＋１、F（１）＝１

より、

　　　F（N）＝２^N―１

N＝６４として、

　　　2⁶⁴-1 (秒)≒1.8×10¹⁹(秒)≒2.1×10¹⁴（日）≒5.8×10¹¹（年）

とまあ大分先のようでちょっと安心しました。

解答・その9

（ペンネ−ム：三角定規）

n枚の円板を柱Aから柱Bに移すのにa_n回の移動手数がかかるとすると，それは右図のように

　　　　a_n−１＋1＋a_n−１

と分解できるから

　　　　a_n＝2a_n−１＋1 ……(1)

初期条件 a_１＝1 のもとで(1)を解いて

　　　　a_n＝2ⁿ −1

n＝64のとき
　2⁶⁴−1 ＝18,446,744,073,709,551,615(秒)
≒584554529391 (年)
≒ 5800 (億年)

この5800億年後が，この問題がいうところの「この世の終わり」です。

しかし，「この世の終わり」を『地球の終わり』と捉えるなら，それはもっともっと最近(?)です。 太陽は現在50億歳，あと50億年で自身の水素エネルギーを消費し尽くし赤色巨星への道を辿ります。 その後地球がどうなるかですが，すべての源の太陽を失うと…… 「この世の終わり」を『人類の終わり』と捉えるなら……あと200年もつかどうか

解答・その10

（ペンネ−ム：夜ふかしのつらいおじさん）

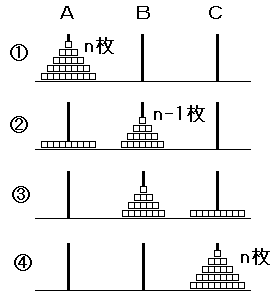
ｎ枚の円盤をＡの柱からＣの柱に移すとき、右の図のような段階があります。
�@は始めの状態です。
�AはＡの柱にあった上のn−1枚の円盤をＢの柱に移した状態です。
�BはＡの柱にあった一番下の１枚の円盤をＣに移した状態です。
�CはＡからＢに移したn−1枚の円盤をＣに移して完成した状態です。
ｆ(n)をn枚の円盤を違う柱に移すのに必要な手数とします。

　　　�@から�Aへは　ｆ(n−1)、
　　　�Aから�Bへは　ｆ(1)（＝ １）、
　　　�Bから�Cへは　ｆ(n−1)

の手数がかかります。つまり、

　　　ｆ(n)＝２ｆ(n−1 )＋１

となります。両辺に１を加えて変形すると、

　　　ｆ(n)＋１＝２｛ｆ(n−1)＋１｝

すると、ｆ(n)＋１は、初項ｆ(1)＋１＝２、公比２の等差数列になるので、

　　　ｆ(n)＋１＝２･２^nー１＝２ⁿ
　　　ｆ(n)＝２ⁿ−１
ここで、n＝64とすると、ｆ(64)＝２⁶⁴−１＝18446744073709551615となります。

さて、
１８４４,６７４４,０７３７,０９５５,１６１５　秒は、
（千八百四十四京、六千七百四十四兆、七百三十七億、九百五十五万、千六百十五　秒）
これを ６０（秒）×６０（分）×２４（時間）×３６５（日）で割ると、
　　　約　５８４９,４２４１,７３５５　年　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・�@
（五千八百四十九億、四千二百四十一万、七千三百五十五　年）
�@を　４５,５０００,００００　年（地球の年齢といわれている）で割ると、

　　　約　１２８．６　倍　（地球が出来て今までの時間の約１２９倍）

�@を　１３７,００００,００００　年（宇宙の年齢、WMAP衛星プロジェクトチーム）で割ると、

　　　約　４２．７　倍　（宇宙が出来て今までの時間の約４３倍）

ともかく気が遠くなるような先にこの世がなくなります。

解答・その11

（ペンネ−ム：SOU）

ｎ枚の移動にかかる最短の手数をf(ｎ)とすると、

　　　ｆ(1)＝1

がわかります。あとは、f(n+1)とf(n)の関係を求め、漸化式に持ち込みます。

まず、f(n+1)とｆ(n)との関係を調べてみます。
3つの柱をそれぞれ左、真ん中、右という名前をつけます。
右の柱にｎ＋１枚の皿が刺さっていて、真中の柱に移動させることにします。
�@まず上からｎ枚だけ左に動かします。
n枚動かすのに必要な手数をf(n)としましたので、この時に必要な手数は f(n)回です。
いま、右にはまだ１枚残ってます。
�A右にある最後の一個を真中に移動させます。ここでかかる手数は１回です。
�B更に左にあるｎ枚を真中に移動させます。この時かかる手数はさっきと同じｆ(n)回です。これで、

　　　ｆ(n+1)＝f(n)+1+f(n)
　　　　　　　＝2f(n)+1

という関係があることが分かりました。これと、

　　　f(1)=1

という条件を使えば帰納的に f(n) が定義されます。

　ｆ(n+1)＝f(n)+1+f(n)
　　　　⇔　f(n+1)+1=2(f(n)+1)　　と変形できる。これは等比数列なので
　　　　⇔　f(n)+1=(f(1)+1)*｛2^n-1｝　と変形できる。
　　　　⇔　f(n)+1=2*{2^n-1}
　　　　⇔　f(n)=(2ⁿ)-1

となるので

　　　f(64)=2⁶⁴-1

となります。すなわち世界が終わるのはその作業を始めたときから考えて

　　　2⁶⁴-1秒後

となります。

解答・その12

（ペンネ−ム：小学名探偵）

（答え）２^６４−１秒後

ｎを円盤の総数とします。
円盤に番号を、小さい順に１〜ｎまで振ります。
ｎ枚の円盤を柱Ａから柱Ｂに移すのに：
ｎ−1枚の円盤をＡからＣに移します。これにより、番号ｎの円盤だけが柱Ａに残ります。
次に、番号ｎの円盤をＡからＢに移します。
最後に、ｎ−１枚の円盤をＣからＢに移します（番号ｎの円盤の上に載せます）。 これから、

　　　A(n)=A(n-1)+ 1+A(n-1)、初項A(1)=1

これを解いて、

　　　A(n)=2ⁿ -1

になります。2ⁿ-1=2ⁿ⁻¹+1+2ⁿ⁻¹ から帰納的に確認できます。

具体的な手順：柱Ａ、Ｂ、Ｃが３角形の頂点の位置に立っていて、Ａ→Ｂ→Ｃ→Ａが 反時計回りだとします。 円盤の枚数ｎが奇数枚のときは、１番小さい円盤を一回置きに（奇数手目のときに） 「反時計回り」で隣の柱に移します。偶数手目では、残り２つの柱 （１番小さい円盤が載っていない２つの柱）の１番上に載っている円盤を比べ （２つの柱の一方が空のときはどんな円盤でも載せることが出来るので空の柱には 無限大の円盤が載っていると考えて）、小さい方を大きい方の上に移します。 円盤の枚数ｎが偶数枚のときは、１番小さい円盤を一回置きに（奇数手目のときに） 「時計回り」で隣の柱に移します。

２進数で考えると、１枚のとき、１
２枚のとき、１＋１＋１＝１０＋１＝１１
３枚のとき、１１＋１＋１１＝１１０＋１＝１１１
となり、ｎ枚のとき、１がｎ個、続く２進数になります。

トーナメント（または、２分枝）で考えると、

　　　　　　　　　　　｜　　　　　　１
　　　　　　　　　｜　　　｜　　　　３
　　　　　　　　｜　｜　｜　｜　　　７（｜の総数）

したがって、ｎ段あれば、1 + 2 +2² +...+2^nｰ1 =2ⁿ -1 です。
円板の数は６４枚なので、世界が終わるまでの時間は、(２^６４−１)秒です。

2⁶⁴-1＝18,446,744,073,709,551,615(秒)

この間、１年が３６５日であり続け（？）、一日の長さが60×60×２４秒であり続け る（？）のであれば、
5849億4241万7355年　26日　7時間　0分　15秒です。
どう考えても、現実の世界の話ではないですね。

上でみたように、柱の数が３本のとき、円盤を移し終えるまでの最小手数は 簡単に求められます。ところが、柱の数が４本以上になると突然、難しくなり、未解 決のようです。

正解者

teki	Toru	巷の夢
小学名探偵	杖のおじさん	SOU
夜ふかしのつらいおじさん	anik	三角定規
aa	蜘蛛の巣城	kirkland

換算の仕方はともかくとして、「2⁶⁴-1」秒というのが答えになります。 約5800億年という途方もない時間になります。
お寄せいただいた解答の多くは、漸化式「a_n=2×a_n-1+1」を見いだし、 それを用いて、一般項である「a_n=2⁶⁴-1」を導いていただきました。
小学名探偵さんの解答の中に２進数に関する記述があり、 これはとても興味を持ちましたので、もう少し詳しく伺いました。

小学名探偵さんより ハノイの塔に関わる僧侶たちは、２進数の世界の住人でした。 かれらにとって、数が２回繰り返されることは、数の桁が１つ繰り上がることです。 かれらには分っていました、ハノイの塔の最小の手順の数が・・・ その数は、移さないといけない円盤がＮ枚あるとき、 いったん、（Ｎ-１）枚を別の塔に移し、そこで、 一番でかい円盤を目的の塔にセットし、それから、 別の塔に移してあった（Ｎ-１）枚をもう一度、移せばよいと。 （Ｎ-１）枚を移す手順は２回繰り返されるのです、その手順の数は一桁上がるです。 かれらは２進数の言葉で話し始めました。 ”１”枚なら、１、 ”１０”枚なら、1が繰り返されて”10”回、これに一番でかい円盤を目的の塔に セットする１回が加わり、 　　　　　　　１０+１＝１１、 ”１１”枚なら、１１０+１＝１１１、 そして、・・・・・・・・・・・・・・・・、 そこへ、コンピュータの世界の人がやってきて、つぎのようなものを記しました。 枚数 状態 左シフト プラス１ 1 0 0 1 2 1 10 11 3 11 110 111 4 111 1110 1111 さらに、別の人がやってきて、最小手順の数と、２のべき乗の数を比べました。 ハノイの塔では、円盤が一枚のとき手順の数は１で２より１少ない。つまり、差は 2-1＝1 ハノイの塔では、円盤が一枚増えるたびに、手順の数は（元の）2倍+1になります。 （円盤が２枚のとき、手順の数は1×2＋1になるが、これを22つまり2×2と比べる と、） 元の差が１なので、２倍した段階（計算の途中）で、差は2になりますが、少ない方 がプラス1されるので、結局、差は１になり、変わりません。 したがって、円盤がＮ枚のとき、最小手順の数は264より、１少ない数です。

漸化式「a_n=2×a_n-1+1」を２進数で考えると、「左シフト＋１」 、目から鱗状態です。つまり、６４枚なら、「１１１１１・・・１」と、２が６４個並ぶわけですよね。 それを１０進数に直すと、蜘蛛の巣城さんの解答にあるように

　　　　２⁶⁴＋２⁶³＋・・・＋２²＋２＋１

となるわけですね。つまり、2⁶⁴-1というわけです。

E-mail 戻る top