86.同心円の分割
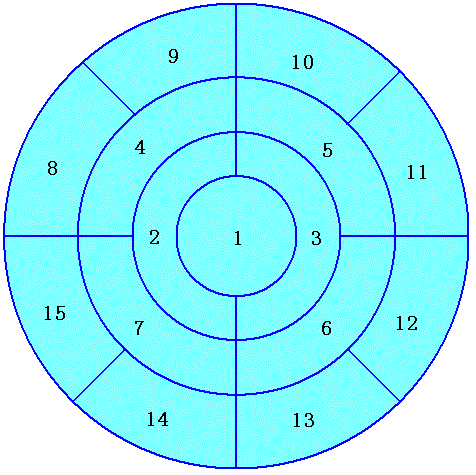
右の図は、四つの同心円を示していて、中央の円には1という番号がついている。 この中央の円と次に続く円によって区切られている部分は、2,3と番号づけられた、それぞれ 合同な図形に分割されている。 同じように、4からはじまる次の円の部分も、 8からはじまるその次の円の部分も、、合同な図形に分割され、順番に番号がつけられている。 これらの番号づけられた15個の図形の面積がすべて同じになるためには、 この四つの同心円の半径の比率はどのようにならなければならないか。
問題の出典
遊びの数学
ヨハンネス・レーマン著
和田秀之訳
啓学出版
答えと解説
答えと解説
解答・その1
(ペンネ−ム:玉村太郎)
同心円の半径比は
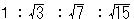

解答・その2
(ペンネ−ム:kiyo)
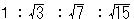

解答・その3
(ペンネ−ム:Mr.X)
円の面積比が 1:3:7:15 だから
円の半径比は
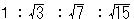 です。
です。

解答・その4
(ペンネ−ム:Toru)
4つの円の面積の比は、1:3:7:15なので半径の比は
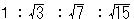
ということでしょうか。

解答・その5
(ペンネ−ム:aa)
一番内側の円の半径を1とすると、面積はπ。
2番目の円の半径をxとすると、「2の面積+3の面積」は、πx2-π
この半分が1の面積と等しいので、(πx2-π)/2=π。
これより、x=√3
同様に、3番目の円の半径をyとすると、(πy2-πx2)/4=π。
これより、y=√7
4番目の円の半径をzとすると、(πz22-πy2)/8=π。
z=√15

解答・その6
(ペンネ−ム:蜘蛛の巣城)
同心円群の内側からn番目の円をCnとし、その半径をRnとすれば
R1:R2:R3:R4
=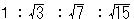 ・・・・・①
・・・・・①
が得られる。手順は後述。
① から帰納すれば、次の推定が得られる。
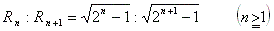 ・・・・・②
・・・・・②
実際、①は ②から演繹される。
従って、② の推定に数学的根拠を与えるためには、次の命題が成り立てばよい。
命題Q 「 比例関係 ② を仮定すれば ③ が得られる。」
③ は次の通り。
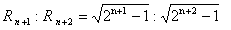 ・・・・・③
・・・・・③
ところで、円Cnのすぐ内側にある2n-1個の合同図形の面積Snについて
条件Sn+1n (n≧1)・・・・・④
が存在する。また、問題の趣旨から明らかに
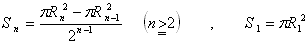 ・・・・・⑤
・・・・・⑤
であることを確認しておこう。
[命題Qについて]
④ ⑤ に拠れば
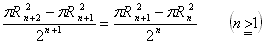
即ち
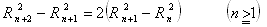 ・・・・・⑥
・・・・・⑥
であるが、この ⑥ に仮定 ② から得られる ⑦ を代入して整理すれば、 比例関係 ③ が得られる。
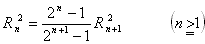 ・・・・・⑦
・・・・・⑦
ところで、冒頭の ① を得る手順は命題Qを証明する手順と同様で、
番号を指定すれば足りる。

解答・その7
(ペンネ−ム:浜田 明巳)
同心円の半径を,小さい方から順にx1,x2,x3,x4とする.
15個の図形の面積が等しいので,
πx12=π(x22−x12)/2=π(x32−x22)/4=π(x42−x32)/8
∴2x12=x22−x12,2(x22−x12)=x32−x22,2(x32−x22)=x42−x32
∴x22=3x12,x32=3x22−2x12,x42=3x32−2x22
∴x22=3x12,x32=7x12,x42=15x12
故に求める半径の比は、小さい方から順に,
x1:x2:x3:x4=
となる.

解答・その8
(ペンネ−ム:やなせ)
まず各同心円の面積は条件から
一番外側は一番内側の15倍(1+2+4+8=15)
外側から二番目は7倍(1+2+4=7)
三番目は3倍(1+2=3)になります。
これから各円の直径の比率を求めると
最内の円の直径を1とした場合
次は √3
そん次は √7
外側の円は√15

解答・その9
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
答え 同心円の分割の半径は、比率、
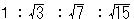 となります。
となります。
小数点以下第3位を四捨五入すると
比率 1:1.73:2.65:3.87 になります。
解説
円の面積は1,3,7,15,31,……………(2*NN−1−1)
,と増加します
同心円のN番目の円の半径をRとすると次の式が成り立ちます。
2*(N(1/2)−1)*3.14=R(1/2)*3.14
R=2*(N(1/2)−1)(1/2)
N=1 R=1(1/2)=1
N=2 R=3(1/2)=1.73
N=3 R=7(1/2)=2.65
N=4 R=15(1/2)=3.87
小数点以下第3位を四捨五入します
今回はエクセルを活用して次のように検証しました
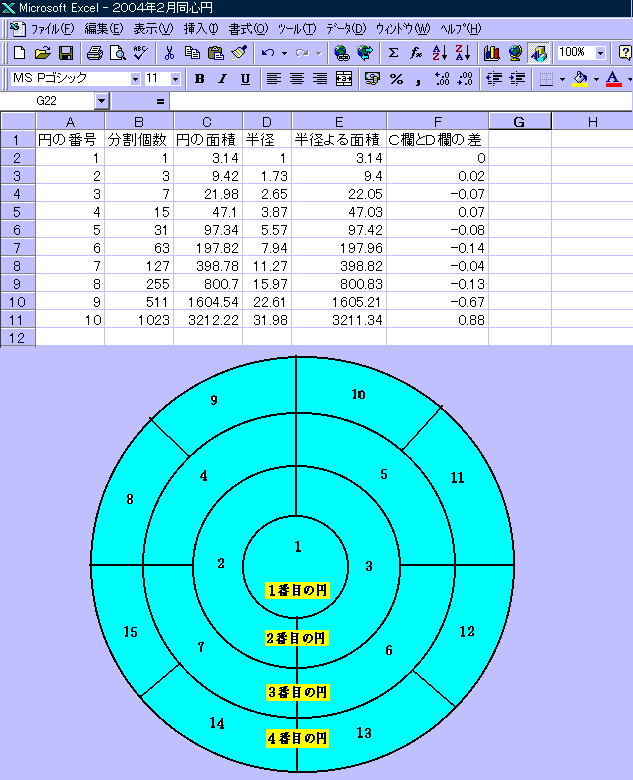
数式入力と解説
A欄は中心の円を1として番号を付番した
B2には2*2^(A2-1)-1(数列により分割面積の数を計算する)
C2にはB2*3.14(分割個数により求めた円の面積)
D2には(INT(B2^(1/2)*100+0.5)/100)(分割個数から半径を求める)
E2にはINT(D2^2*3.14*100+0.5)/100(半径より求めた面積)
F2にはC2-E2(C欄とE欄との計算の差)小数点以下第3位を四捨五入した面積との差なので差は出ます
すべての数式をドラック・アンド・ドロップで円番号10までコピーーする
数式の所を選択して右クリック、コピーを選択してエクセルに貼り付けて試してみてください。

解答・その10
(ペンネ−ム:巷の夢)
今4個の同心円の半径をr1、r2、r3及びr4とすると、
題意より、
πr22=3πr12
πr32=7πr12
πr42=15πr12が成り立つ。
因って、
r1:r2:r3:r4
= 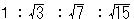 が求めるものである。
が求めるものである。

解答・その11
(ペンネ−ム:teki)
答え 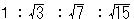
この問題、最初はもう少しややこしい計算が必要かと思われたんですが、
次のように考えると、あっさり解けました。
分割された図形の面積はどれも等しいのですから、番号1の円の面積を1とすると、
2番目の円はその3倍、3番目の円はその7倍、一番大きい円はその12倍の面積です。
円の面積は半径の2乗に比例するので、半径の比は、
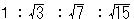 となります。
となります。

解答・その12
(ペンネ−ム:UnderBird)
4つの同心円の半径をr1,r2,r3,r4
(r1<r2<r3<r4)とする。
また、1と番号づけられた半径r1の円の面積をSとすると、
πr12=S
πr22=3S
πr32=7S
πr42=15S
より、
r1=sqrt(S/π)
r2=sqrt(3S/π)
r3=sqrt(7S/π)
r4=sqrt(15S/π)
だから、
r1:r2:r3:r4= 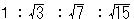

解答・その13
(ペンネ−ム:ユージ)
一番小さい円の面積を1とすると、円の面積は小さい順に
1、3、7、15
面積は半径の二乗だから、円の半径は小さい順に、
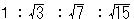
よって円の半径の比率は小さい順に、
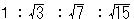
となる。

解答・その14
(ペンネ−ム:小学名探偵)
答え 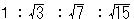
一番内側の円の面積を1とすると、二番目、三番目、四番目の円の面積は、それぞれ
3、7、15になります。(嬉しいことに1,3,7,15の数字は図面に書かれてますね)
相似な図形の対応する長さ(ここでは半径)同士の比は面積の比の平方根に
比例します。
逆に言えば、対応する長さの二乗の比が面積比になります。

解答・その15
(ペンネ−ム:三角定規)
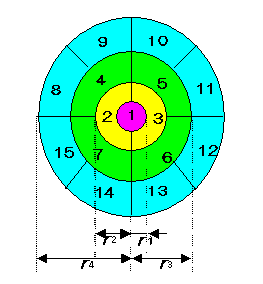
右図のように4つの円の半径を r1、r2、r3、r4
とすると、
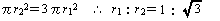
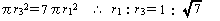
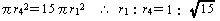
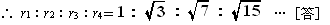
同じルールでn 個の同心円を作るとすると,その半径 rn は、
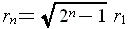

解答・その16
(ペンネ−ム:夜ふかしのつらいおじさん)
四つの円の面積の比率は、小さい順に、次のようになります。
1:(1+2):(1+2+4):(1+2+4+8)=1:3:7:15
面積は、半径の平方に比例するので、その平方根が半径の比率です。
だから、次のようになります。
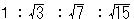
この問題を考えていて思いついた問題を書きます。そんなに難しくないので考え
てみてください。2つとも同じ答になります。
【類題】
1.n個の同心円がある。半径の小さい順に円に番号をつける。
k番目と(k+1)番目の円の間は、2k 個の合同な図形に分割されている。
(kは、1以上、(n−1)以下)
これら (2n −1)個の図形の面積が全て同じならば、nが十分大きいとき、
n番目と(n−1)番目の円の直径の比は、どんな値に近づくか考えなさい。
2.n個の同心円がある。半径の小さい順に円に番号をつける。
k番目と(k+1)番目の円の間は、(k+1) 個の合同な図形に分割されている。
(kは、1以上、(n−1)以下)
これら 1/2・n(n+1)個の図形の面積が全て同じならば、nが十分大きいとき、
n番目と(n−1)番目の円の直径の差は、どんな値に近づくか考えなさい。

解答・その17
(ペンネ−ム:kirkland)
| 先生 | 「今月の問題は平方根を使うので、小学生の君には無理だと思うんだけど。」 |
| A君 | 「だったら、そのヘーホーコンっていうのを教えて下さいよ。」 |
| 先生 | 「面倒だなぁ。例えば、円の面積を16倍にしようと思ったら、その半径を何倍にすればいいか分かる?」 |
| A君 | 「なめてもらったら困りますねぇ〜。16倍とか8倍とか言うと思ったんでしょう! 残念でした、4×4=16だから半径を4倍にすれば面積は16倍になりますよ。」 |
| 先生 | 「正解。では、面積を2倍にしようとすると?」 |
| A君 | 「???先生は、九九を知ってますか?そんな数は、ありませんよ。だって、1×1=1だし、 2×2=4ですもの。同じ数を2回掛け合わせて2になる数は、ないんじゃないですか?」 |
| 先生 | 「だから、面倒なことはイヤだって言ったじゃないか。整数だけで考えるからダメなんだよ! 小数もふくめて探しなさい。」 |
| A君 | 「そんなことを言われても、1.4×1.4=1.96で1.5×1.5=2.25なんだから、1.4と1.5の間というぐら いしか分かりません。」 |
| 先生 | 「だいたい1.41421356ぐらいだよ。」 |
| A君 | 「1.41421356×1.41421356=1.9999999932878736なので、2に近いですね。うーん、電卓って便利。 でも、まだ2じゃないですね。」 |
| 先生 | 「実際には、1.414213562373095048801688724209698078569671875376……とずっと続いていく
小数なんだよ。細かい理屈は抜きにするけど、この数は書ききれないので、とりあえず と
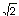 書くことにしているわけだ。『ルート2』と読もう。」 書くことにしているわけだ。『ルート2』と読もう。」
|
| A君 | 「ほほう、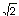 × ×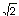 =2というわけですね。ところで、どうやって計算したんですか?」 =2というわけですね。ところで、どうやって計算したんですか?」
|
| 先生 | 「それはまたの機会にでも教えましょう。…と逃げつつ、 とりあえずは、1.41421356は『一夜一夜に人見頃』とでも覚えておきなさい。」 |
| A君 | 「ふ〜ん。では、 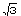 × × 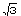 =3なんですよね。 =3なんですよね。
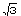 はどれぐらいの数ですか?」 はどれぐらいの数ですか?」
|
| 先生 | 「 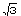 ≒1.7320508は『人並みにおごれや』です。
ちなみに ≒1.7320508は『人並みにおごれや』です。
ちなみに 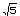 ≒2.2360679『富士山麓オーム鳴く』です。」 ≒2.2360679『富士山麓オーム鳴く』です。」
|
| A君 | 「これさえ分かれば簡単なので、問題にいきま〜す。
円の面積の比は、小さい方から順に1:3:7:15
になっているので、半径の比は 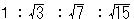 ですね。」 ですね。」
|
| 先生 | 「まぁ正解だ。まだスペースがあるので、もう少し色々な言葉を教えておきましょう。同じ数を2回掛け あわせることを平方とか2乗とか言って、その数の右上に小さく2を書きます。例えば、3×3は 32と書いて、『3の平方』または『3の2乗』とか読むわけだ。」 |
| A君 | 「あっ、ひょっとして面積の単位で『m2』というのは、そういうことだったんですね。」 |
| 先生 | 「その通り。同じ数を3回掛け合わせることは、立方とか単に3乗とか言ったりします。」 |
| A君 | 「只今×只今×只今=只今参上!ってな感じですね!」 |
| 先生 | 「軽く無視して話を進めるけど、逆に、平方してその数になる数のことを平方根というわけだ。
16=42だから16の平方根は4、3=( 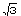 )2だから3の平方根は )2だから3の平方根は
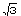 だ。本当はちょっと違うんだけど
ね。ちなみに だ。本当はちょっと違うんだけど
ね。ちなみに 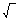 の記号は日本語で根号っていうんだよ。」 の記号は日本語で根号っていうんだよ。」
|
| A君 | 「いや〜、今月は色々と勉強になりましたな〜。新しい記号をさっそく使ってみましょう。
先生、問題です。さて、次の山の名前は?問1 山2 問2 |
| 先生 | 「???」 |
| A君 | 「ヒントでーす。どちらの山も僕の家(奈良県)から見えますよ。さ〜て、みなさんも地図で探 して下さいね〜。では、さいなら〜〜。」 |

解答・その18
(ペンネ−ム:yokodon)
番号のついた区切りの部分を、番号 n に対して「区画 n」と呼ぶことにし、区画
n の面積を Sn とします。
図にある円の半径を小さい方から順番に r1, r2, r3, r4とすると、題意から、
S1 = π・(r1)2
S2 = S3 = π・{(r2)2 - (r2)2}/2
S4 = S5 = S6 = S7 = π・{(r3)2 - (r_2)2}/4
S8 = ... = S15 = π・{(r4)2 - (r3)2}/8
且つ、
S1 = S2 = S4 = S8
・・・なので、結局
| π・(r1) | = π・{(r2)2 - (r1)2}/2 |
| = π・{(r3)2 - (r2)2}/4 | |
| = π・{(r4)2 - (r3)2}/8 |
を得ます。これを整理して、
r2 = √3・r1 、r3 = √7・r1 、r4 = √15・r1
従って、求める比は
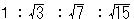 ・・・(答)
・・・(答)同様に、題意にある規則でドンドン外側に区画を作っていくと、m 番目の円の半径
rm は 1 番目の円の半径を r1 として
rm = √(2m - 1)・r1
になるのでしょうか。

正解者
| 巷の夢 | teki | Toru |
| やなせ | 小学名探偵 | kiyo |
| 夜ふかしのつらいおじさん | 杖のおじさん | Mr.X |
| 浜田 明巳 | 玉村太郎 | ユージ |
| 蜘蛛の巣城 | aa | kirkland |
| UnderBird | 三角定規 | yokodon |

まとめ
ドーナツ部分に注目して、1,2,4,8,・・・等比数列か・・・と、 考えるとちょっと大変ですが、 「同心円」に注目して、円の中にピースがいくつあるか、と考えると 答えは図の中にあります。
1:3:7:15
ピースの面積はどれも等しいのですから、これが面積比です。 面積比は、相似比(長さの比)の2乗比ですから、
ですね。
ただし、一般的な比を求めようとすると、やはりドーナツに注目せざるをえません。 ドーナツ部分の面積は、1,2,4,8・・・という初項が1、公比が2の等比数列になっています。 円の面積はそれを足していけばいいわけですから、 中央からn番目の円の面積は、この等比数列の部分和Snということになります。 1番の円の面積をS1として、
Sn ={1−2n}/(1−2)・S1 =(2nー1)・S1
従って、三角定規さんが求めてくださったように、
n番目の円の半径 rn は、
となります。夜ふかしのつらいおじさん、 A君(kirklandさん)から宿題が出されています。 皆さん、考えてみてください。

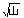 」
」 E-mail
E-mail
 戻る
戻る
 top
top