侾俀亊侾俇俈偺挿曽宍傪丄偱偒傞偩偗悢偑彮側偄惓曽宍偵暘妱偟偰偔偩偝偄丅
Weekend Mathematics乛栤戣乛栤戣85
俉俆丏俀侽侽係擭偺栤戣
侾俀亊侾俇俈偺挿曽宍傪丄偱偒傞偩偗悢偑彮側偄惓曽宍偵暘妱偟偰偔偩偝偄丅
僷僘儖傛傝柺敀偄拞妛擖帋偺嶼悢
僺乕僞乕丒僼儔儞僋儖挊
島択幮
夝摎丒偦偺1
乮儁儞僱亅儉丗Hiro乯
摎偊丂俀侽屄
夝摎丒偦偺2
乮儁儞僱亅儉丗kiyo乯
12*167=2004=(12*12)*13+(8*8)*1+(4*4)*2+(3*3)*4
13+1+2+4=20
20屄丅
夝摎丒偦偺3
乮儁儞僱亅儉丗岼偺柌乯
惓曽宍
丂丂侾俀亊侾俀仺侾俁屄
丂丂俉亊俉仺侾屄
丂丂係亊係仺俀屄
丂丂俁亊俁仺係屄
丂場偭偰慡晹偱俀侽屄偺惓曽宍偵暘妱偡傞偺偑嵟彫屄悢偲側傝傑偡丅
夝摎丒偦偺4
乮儁儞僱亅儉丗摻柤婓朷乯
惓曽宍偺悢偑彮側偄曽偑偄偄偺偱傑偢丄堦曈偑侾俀僙儞僠偺惓曽宍偱廲偵暘妱偟傑偡丅
丂丂丂167亐12亖13偁傑傝11丂丂師偼丄墶偵堦曈侾侾僙儞僠偺惓曽宍偱暘妱丅
丂丂丂12亐11亖1偁傑傝1丂丂丂丂傕偆堦搙廲偵堦曈侾僙儞僠偺惓曽宍偱暘妱丅
丂丂丂11亐1亖11
偲丄偡傞偲彫偝偄惓曽宍偑偨偔偝傫偱偒偰偟傑偆偺偱丄堦曈偑侾僙儞僠偺惓曽宍傪嶌傜側偄岺晇傪 偡傟偽椙偄偲峫偊偰丄堦曈侾俀僙儞僠偺惓曽宍偱暘妱偟偨屻偺廲侾俀僙儞僠墶侾侾僙儞僠偺挿曽宍傪 俁亊俁偺惓曽宍係屄偲俉亊俉偺惓曽宍侾屄偲係亊係偺惓曽宍俀屄偵暘妱偟傑偡丅
偮傑傝丄13+4+2+1偱俀侽屄丒丒丒偐側傽丠
夝摎丒偦偺5
乮儁儞僱亅儉丗teki乯
摎偊丂侾俀亊侾俀偑侾俁枃丄俉亊俉偑侾枃丄係亊係偑俀枃丄俁亊俁偑係枃丂寁俀侽枃
侾俀亊侾俀傪偱偒傞偩偗懡偔愗傝庢傝丄巆偭偨侾俀亊侾侾傪嵟彫屄悢偱暘妱 偡傞曽朄傪峫偊傑偟偨丅
侾俀亊侾侾偐傜丄俉亊俉傪侾屄愗傝庢傝丄巆偭偨L帤宆偺晹暘傪係亊係偑俀枃偲俁亊俁 偑係枃偵暘妱偡傟偽丄寁俈枃偱暘妱偱偒傑偡偹丅
夝摎丒偦偺6
乮儁儞僱亅儉丗俶偲乣乯
丂侾俀亊侾俀偺惓曽宍丒丒丒丒丒丒丒侾俁屄
丂丂俉亊丂俉偺惓曽宍丒丒丒丒丒丒丒丂侾屄
丂丂係亊丂係偺惓曽宍丒丒丒丒丒丒丒丂俀屄
丂丂俁亊丂俁偺惓曽宍丒丒丒丒丒丒丒丂係屄
偺崌寁俀侽屄偑嵟彫偐側偀偲巚偭偰偄傑偡丅
偱傕丄徹柧傕偱偒偰偄傑偣傫偟丄斀椺傪尒偮偗傛偆偲巚偭偰傕尒偮偗傜傟 傑偣傫丅傒側偝傫偺徹柧傪妝偟傒偵偟偰偄傑偡丅 偲傝偁偊偢憲偭偰偍偒傑偡偹丅
夝摎丒偦偺7
乮儁儞僱亅儉丗彫妛柤扵掋乯
摎偊丂20屄
嵟弶偵12仏12偺惓曽宍傪愗傝庢偭偰偄偔偺偼摨偠偱偡偑丄師偵巆偭偨 11仏12偺惓曽宍偺張棟偑堘偄傑偡丅
嘆8仏8偺惓曽宍傪愗傝庢傞乮嵍忋乯
嘇4仏4偺惓曽宍傪愗傝庢傟傞偩偗愗傝庢傞乮嘆偺壓乯
嘊巆偭偨晹暘傪3仏3偺惓曽宍偱杽傔傞
偡傞偲摎偊偼13+1+2+4偺20屄偲側傝傑偡丂丂
夝摎丒偦偺8
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊俀侽屄偱偡
嵟弶偼俀俆屄偲巚偄傑偟偨偑丄偱偒傞偩偗悢偑彮側偄惓曽宍偵暘妱偟偰偔偩偝偄丄 偲栤戣偑弌偰偄傑偡偺偱庤寁嶼偱 傗偭偰尒傑偟偨丅偦偺寢壥俀侽屄偩偲敾柧偟傑偟偨丅嵟屻傑偱丄尒偰偔偩偝偄両
娫堘偄偺傗傝曽
丂丂俇侾俈乛侾俀亖侾俁丏俋侾俇俇乧丂丂侾俁偲梋傝丂俇侾俈亅乮侾俀仏侾俁乯亖侾侾
丂丂侾俀乛侾侾亖侾丏侽俋乧丂丂丂丂丂丂丂侾偲梋傝丂丂侾俀亅乮侾侾仏侾乯亖侾
丂丂侾侾乛侾亖侾侾丂丂丂丂丂丂丂丂丂丂侾侾偲梋傝丂侽
廬偭偰侾俁亄侾亄侾侾亖俀俆屄偱偡
崱夞傕CASIO(僇僔僆)丂FX乗俉俈侽P丂 CASIO(僇僔僆)丂FX乗俉俋侽P丂偺億働僢僩僐 儞僺儏乕僞乕乮億働僐儞乯偱僾儘僌儔儉傪嶌偭偰傒傑偟偨丅
僾儘僌儔儉偼師偺捠傝偱偡丅
侾侽丂俹俼俬俶俿乬僙僀儂僂働僀丂僯丂僽儞僇僣丂僾儘僌儔儉乭 俀侽丂俬俶俹倀俿乬儓僐乭丟俙 俁侽丂俬俶俹倀俿乬僞僥乭丟俛 係侽丂俿亖侽 俆侽丂俬俥丂俙亜俛丂俿俫俤俶丂俠亖俙丗俙亖俛丗俛亖俠 俇侽丂倄亖俛乛俙丗倅亖俬俶俿丂倄丗俛亖俛亅俙仏倅丗倂亖倄亅倅 俈侽丂俿亖俿亄倅 俉侽丂俬俥丂倂亜侽丂俿俫俤俶丂俆侽 俋侽丂俛俤俤俹丗俹俼俬俶俿乬僙僀儂僂働僀丂僴乭丟倀丟乬僐丂僨僗乭 侾侽侽丂俧俷俿俷丂俀侽
僾儘僌儔儉夝愢
俀侽峴丄俁侽峴偱僞僥丄儓僐傪擖椡偟傑偡丅 俆侽峴偱僞僥丄儓僐傪彫偝偄弴偵暲傋懼偊偰偄傑偡偺偱俀侽峴偱偳偪傜偱傕愭偵擖椡偟偰椙偄偺偱偡丅
俿偼惓曽宍偺憤崌寁傪僇僂儞僩偡傞曄悢偱偡丅倅偼惓曽宍偑偄偔偮弌棃傞偐寁嶼偟偰偄傑偡丅
倂偼惓曽宍傪嶌偭偨偲偒偺偁傑偭偨晹暘偱偡丅俉侽峴偱梋偭偨晹暘偑偁傞偲敾抐偝傟傞偲 俆侽峴偵旘傫偱梋偭偨晹暘偱偄偔偮惓曽宍偑弌棃傞偐寁嶼傪峴偄傑偡丅
俋侽峴偱俛俤俤俹壒傪柭傜偟俹俼俬俶俿暥偱寢壥傪弌偟傑偡丅
僾儘僌儔儉偺嶌傝曽偄傠偄傠偁傝傑偡偺偱嶌偭偰尒傞偲柺敀偄偱偡丅
偙偺僾儘僌儔儉傪幚峴偡傞偲
儓僐丠丂偲暦偄偰偒傑偡偺偱侾俇俈偲擖椡偟傑偡丅
師偵偨偰丠偲暦偄偰偒傑偡偺偱侾俀偲擖椡偟傑偡丅
俤倃俤僉乕傪墴偡偲侾昩屻丂僙僀儂僂働僀僴丂俀俆丂僐丂僨僗丂偲丂丂寢壥傪弌偟傑偡丅
僞僥丂丄儓僐丂丄揔摉偵擖椡偟偰尒偰偔偩偝偄丅
儓僐侾俀俁係俆俇俈俉俋侽丄僞僥侾俀俁係俆傪擖椡偟偰尒傑偟偨丅
摨偠偔侾昩屻丄侾侽侽係侾俉屄偲弌傑偟偨丅
娫堘偄偲婥偯偄偰傗傝捈偟偨傕偺
偪傚偭偲懸偰傛両偙偺摎偊偱偼栤戣偺庡巪偱偁傞偱偒傞偩偗悢偑彮側偄惓曽宍偵暘妱偟偰偔偩偝偄偲偄 偆尵梩偑斀塮偝傟偰偄側偄側両偦傟偱偼庤寁嶼偱傗偭偰傒傛偆両
嵟弶偺惓曽宍偼
侾俇俈乛侾俀偱侾俁屄弌棃傞丅
廬偭偰侾俀仏侾俁亖侾俆俇丂巆傝侾侾亊侾俀偵惓曽宍偑婔偮弌棃傞偐峫偊傟偽偄偄
廲丂俁亊俁丂偺惓曽宍丂係屄
塃偵俉亊俉丂偺惓曽宍丂侾屄
壓塃懁偵係亊係丂偺惓曽宍丂俀屄
崌寁丂俀侽屄偱偡
夝摎丒偦偺9
乮儁儞僱亅儉丗傗側偣乯
傑偢嵟弶偵侾俀亊侾俀偺惓曽宍傪墶偵侾俁屄嶌傝傑偡丅
巆傝偺侾俀亊侾侾傪俉亊俉亖侾屄偲係亊係亖俀屄丂俁亊俁亖係屄偱偟偨偐偹丅
偮傑傝俀侽屄偱偟偨偐丠
夝摎丒偦偺10
乮儁儞僱亅儉丗帥榚丂將乯
傑偢偼丂侾俀亊侾俀偺惓曽宍傪侾俁屄偲傞偲丂侾俀亊侾侾偺挿曽宍偑巆傝傑偡丅
師偵偦偺侾俀亊侾侾偺挿曽宍傪廲侾俀丄墶侾侾偲偟偰堦斣戝偒偄侾侾亊侾侾偺惓曽宍偐傜弴斣偵 嵍偺忋偺嬿偵偲偭偰巆偭偨僗儁乕僗偐傜壗屄偐偺惓曽宍傪愗傝弌偟偰偄偒傑偟偨丄偦偆偡傞偲 嵍忋嬿偵俉亊俉偺惓曽宍傪偲偭偨偲偒偑丂侾俀亊侾侾傪嵟彫偺俈屄偱暘妱弌棃傑偟偨丅
偮傑傝偼偙偆偱偡丄恾偑側偔偰暘傝擄偄偲偍傕偄傑偡偑丂
嵍忋嬿偵8亊8偑侾屄丄懘偺壓偵係亊係偑俀屄丄塃嬿偵偼忋偐傜壓傊丂俁亊俁偑係屄暲傃傑偟偰 寁俈屄偱嵟弶偺侾俁屄偲懌偟偰丂俀侽屄偺惓曽宍偵暘妱弌棃傑偟偨丅
夝摎丒偦偺11
乮儁儞僱亅儉丗Toru乯
側傞傎偳侾俀x侾俇俈亖俀侽侽係偲偄偆傢偗偱偡偹丅
侾俀x侾俀傪侾俁屄丄俉x俉傪侾屄丄係x係傪俀屄丄俁x俁傪係屄偲偡傞偲寁俀侽屄偱偱 偒傑偡丅
偙傟傛傝彮側偄悢偱偱偒傞偐偳偆偐専摙偟側偔偰偼偄偗傑偣傫偑丄傑偢丄侾俀x侾俀 傪巊傢側偄偲偡傞偲丄侾俋屄埲壓偱偼偱偒側偄偺偱丄彮側偔偲傕堦偮偼巊偆丅偙傟傪 抂傊傕偭偰偒偰愗傝棧偡偲丄侾俀x侾俆俆傪侾俉屄埲壓偱偱偒傞偐専摙偲偄偆偙偲偵 側傝傑偡偑丄偙偙偱傑偨侾俀x侾俀傪巊傢側偄偲偡傞偲丄偲摨偠傛偆偵峫偊偰偄偔偲 乮俀俁x侾侾偺偁偨傝偼丄嵟弶傎偳娙扨偱偼偁傝傑偣傫偑乯寢嬊丄侾俀x侾侾偑俇屄埲 壓偱偱偒傞偐偲偄偆偙偲偵側傞偐偲巚偄傑偡丅偙偺挿曽宍偺侾俀偺曈偺曅懁偵惓曽宍 傪俀偮暲傋傞応崌丄俁偮暲傋傞応崌偲偄偆傛偆偵偄傠偄傠専摙偟偰傕丄寢嬊俇偮埲壓 偱偼偱偒偦偆傕側偄偺偱丄俀侽屄偑嵟彫偺傛偆偵巚傢傟傑偡丅
夝摎丒偦偺12
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
摎偼丄俀侽屄偱偡丅
侾俀亊侾俇俈偺挿曽宍傪丄偱偒傞偩偗悢偑彮側偄惓曽宍偵暘妱偡傞応崌丄 傑偢堦斣戝偒側侾曈侾俀偺惓曽宍傪側傞傋偔懡偔庢傝傑偡丅 侾俇俈亐侾俀亖侾俁梋傝侾侾側偺偱丄弶傔偵侾俁屄庢傝傑偡丅
師偵丄巆偭偨侾俀亊侾侾偺挿曽宍偵偮偄偰峫偊傑偡丅 巆傝偺挿曽宍偱庢傝偆傞惓曽宍偺侾曈偺挿偝偱応崌暘偗傪偟偰幚嵺偵彂偄偰傒傑偡丅 偡傞偲師偺傛偆側寢壥偵側傝傑偡丅昞偺拞偺悢偼丄惓曽宍偺屄悢偱偡丅
惓曽宍偺侾曈 11 10 9 8 7 6 5 4 3 2 1 惓曽宍偺屄悢 惓曽宍偺柺愊寁 恾侾 1 丂 丂 丂 丂 丂 丂 丂 丂 丂 11 12 132 恾俀 丂 1 丂 丂 丂 丂 丂 丂 丂 5 12 18 132 恾俁 丂 丂 1 丂 丂 丂 丂 丂 3 6 丂 10 132 恾係 丂 丂 丂 1 丂 丂 丂 2 4 丂 丂 7 132 恾俆 丂 丂 丂 丂 1 丂 1 3 丂 2 2 9 132 恾俇 丂 丂 丂 丂 丂 2 2 丂 丂 2 2 8 132
恾係偺応崌偑堦斣屄悢偑彮側偔側傝丄侾俁亄俈亖俀侽屄偱偡丅
夝摎丒偦偺13
乮儁儞僱亅儉丗嶰妏掕婯乯
2004亖12亊167 亖12亊(12亊13亄11)
偱偁傞偐傜丆挿曽宍偺堦抂偐傜12亊12偺惓曽宍傪13屄偲傝丆巆傝偺12亊11偺晹暘傪惓曽宍偵暘妱偡傞丅
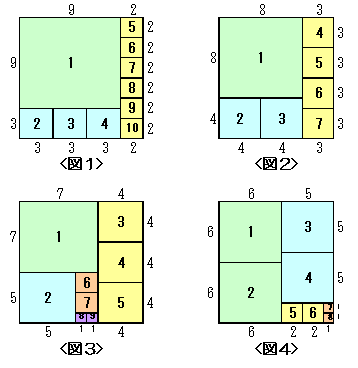
塃恾偺4偮偺応崌傪挷傋傟偽廫暘偱偟傚偆丅寢壥偼丆亙恾俀亜 偺7屄偑嵟彫丅
忋偺13屄偲偁傢偣偰丂丂乵摎乶20 屄
夝摎丒偦偺14
乮儁儞僱亅儉丗kirkland乯
俙孨 乽傆偭偐乣乣偮!!慡崙俀壄7000枩恖偺奆偝傫丄偍懸偨偣偟傑偟偨乣乣両乿 愭惗 乽暿偵扤傕懸偭偰側偄偧丅偟偐傕丄擔杮偺恖岥偼偦傫側偵懡偔側偄偧丅乿 俙孨 乽偝偀偰崲偭偨偙偲偵丄崱寧偼栤戣暥偑僔儞僾儖偡偓偰儃働傛偆偑偁傝傑偣傫丅崲偭偨丄崲偭偨丅挿偔側傝偦偆側偺偱丄 憗懍偄偒傑偡丅傑偢偼12亊12偺惓曽宍偑13屄偱偒傑偡偹丅巆偭偨12亊11偺挿曽宍傪暘偗傞傢偗偱偡偑丄偙偙偱挷 巕偵忔偭偰11亊11偺惓曽宍傪偮偔偭偰偟傑偆偲丄11亊侾偺挿曽宍偑巆偭偰傑偨傑偨崲偭偪傖偆傢偗偱偡傛丅 偙傟偩偲侾亊侾偺惓曽宍傪11屄偮偔傞偟偐側偄傢偗偩偐傜丄屄悢偑懡偔側偭偰偟傑偄傑偡丅恖惗偁傫傑傝梸挘傜偢 偵丄彮偟峊偊偺曽偑傛傠偟偄傛偆偱偡丅乿 愭惗 乽暿偵恖惗傪岅傞傎偳偺栤戣偱偼柍偄偲巚偆偑丄12亊11偺挿曽宍傪偳偺傛偆偵暘偗傞偐偩偹丅乿 俙孨
乽偄傠偄傠偲幚尡偟偰傒偨偺偱偡偑丄塃恾偺傛偆偵偡傞偲俈屄偵暘偗傜傟傑偡丅 偙傟偑摎偊偩偲巚偆傫偱偡偗偳丅偁偭丄偦傟偧傟偺惓曽宍偺拞偵偁傞悢帤偼堦曈偺挿偝偱偡傛丅乿
愭惗 乽偊傜偔庤敳偒側揥奐偩側丅傕偆彮偟挌擩偵傗偭偨曽偑偄偄傫偠傖側偄偺丠乿 俙孨 乽偄傗丄崱夞偼偙偙偐傜偑挿偄傫偱偡傛丅偲偄偆偺傕丄杮摉偵偙傟傛傝彮側偔側傜側偄傫偱偡偐丠 暘偗曽傪岺晇偟偨傝丄堦曈傪暘悢偵偟偨傝偡傞偲丄傕偭偲彮側偄応崌傕偁傞偐傕偟傟傑偣傫傛丅乿 愭惗 乽偆乣傫丄偦傟傕堦棟偁傞偹偊丅偱偼丄俇屄埲壓偵暘偗傞偙偲偺偱偒傞挿曽宍偺廲墶偺斾傪曅偭抂偐傜挷傋偰傒傛偆丅 傑偢偼丄俀屄偺惓曽宍偵暘偗傞偙偲偺偱偒傞挿曽宍偺廲墶偺斾偼丠乿 俙孨 乽偙傟偼娙扨丅侾丗俀偺挿曽宍偱偡傛偹丅俀丗侾偱傕摨偠帠偱偡偗偳丅乿
愭惗 乽偱偼丄俁偮偺惓曽宍偵暘偗傞偙偲偺偱偒傞挿曽宍偺応崌偼丠乿 俙孨 乽壓恾偺傛偆偵侾丗俁偲俀丗俁偺挿曽宍偱偡丅乿
愭惗 乽係偮偼丠乿 俙孨 乽傑偨傑偨恾傪昤偒傑偡丅侾丗係偲俁丗係偲俀丗俆偲俁丗俆偱偡偹丅乿
愭惗 乽偦傠偦傠婯懃惈偵婥晅偄偨偐側丠俆偮偺応崌偼丠乿 俙孨 乽係偮偺惓曽宍偱偱偒偨挿曽宍偺廲偐墶偵惓曽宍傪偝傜偵侾偮晅偗壛偊傟偽偄偄偺偩偐傜乧乧丅倎丗倐偺挿曽宍偵惓曽 宍傪侾偮偔偭偮偗傞偲丄倎丗(倎亄倐)偲倐丗(倎亄倐)偺俀庬椶偺挿曽宍偑偱偒傑偡丅椺偊偽丄侾丗係偺挿曽宍偵惓曽 宍傪侾偮偔偭偮偗偰偱偒傞侾丗俆偺挿曽宍偲係丗俆偺挿曽宍偼偲傕偵俆偮偺惓曽宍偵暘妱偡傞偙偲偑偱偒傞偼偢偱 偡丅偙傟側傜丄偄偪偄偪恾傪昤偐側偔偰傕偄偄偱偡偹丅乿 愭惗 乽偄偄傫偠傖側偄偺丅乿 俙孨 乽偲偄偆傢偗偱丄俆偮偵暘偗傜傟傞偺偼侾丗俆丄係丗俆丄俁丗俈丄係丗俈丄俀丗俈丄俆丗俈丄俁丗俉丄俆丗俉偺 俉僷僞乕儞偱偡偹丅乿 愭惗 乽孨傕傑偩傑偩偩偹偉丅俆亖係亄侾偩偗偐丠俆亖俁亄俀偭偰偄偆応崌傕偁傞偩傠偆偵丅乿 俙孨 乽偁偭偦偆偐両俁偮偵暘妱壜擻側挿曽宍偲俀偮偵偵暘妱壜擻側挿曽宍傪偔偭偮偗偰傕偄偄傢偗偐丅 偡傞偲丄壓恾偺傛偆側俆丗俇偲俇丗俈偺挿曽宍傕俆偮偵暘妱偱偒傑偡偹丅乿
愭惗 乽偝偰俇偮偩丅乿 俙孨 乽俇亖俆亄侾偺僷僞乕儞偼娙扨丅傑偢丄侾丗俆偐傜侾丗俇丄俆丗俇偑偮偔傟傑偡丅偍偭偲丄俆丗俇偼俆偮偱偱偒傞傫偩 偭偨丅係丗俋丄俆丗俋丄俁丗10丄俈丗10丄係丗11丄俈丗11丄俀丗俋丄俈丗俋丄俆丗12丄俈丗12丄俁丗11丄俉丗11丄 俆丗13丄俉丗13丄俆丗11丄俇丗11丄俇丗13丄俈丗13偱偡偹丅俇亖係亄俀偺僷僞乕儞偼恾傪昤偗偽暘偐傝傗偡偄傫偩 偗偳柺搢側偺偱丄俋丗10偲10丗11丅俇亖俁亄俁偺僷僞乕儞偼僟儊丅偙傫側傕傫偱偳偆偱偟傚偆丠偲偄偭偰傕丄偙傫 側悢帤偺梾楍偽偐傝偠傖偀丄扤傕偪傖傫偲撉傑側偄婥偑偟傑偡偑丅乿 愭惗 乽傆傆傆偭丄彮乆僀儞僠僉廘偄偑丄壓恾偺傛偆偵偡傞偲11丗13傕俇偮偱俷俲側傫偩傛丅乿
俙孨 乽乧乧乧丅傑偁丄偄偢傟偵偣傛11丗12偺挿曽宍偼俇屄埲壓偺惓曽宍偵偼暘妱偱偒側偄偲偄偆偙偲偱偡偹丅偲尵偆傢偗偱丄弶傔偺梊憐捠傝20屄偑嵟彮偱偡偹丅乿 愭惗 乽惓曽宍傪侾偮偢偮壛偊偰偄偔僷僞乕儞偼搶岺戝偺栤戣偵偁傞傫偩偗偳丄偁傟側傜彫妛惗偱傕夝偗傞偲巚偆傛丅乿 俙孨 乽僩乕僐乕戝丠搳崀戝偭偰曔椄偽偭偐傝丠偼偨傑偨丄摢岝戝偭偰僴僎偽偭偐傝丠乿 愭惗 乽傗傔側偝偄偭偰丅嬯忣偑偔傞傛両乿 俙孨 乽偱偼丄偙傫側姶偠偱搳峞両乿
惓夝幰
kiyo teki 忨偺偍偠偝傫 嶰妏掕婯 岼偺柌 Hiro Toru 栭傆偐偟偺偮傜偄偍偠偝傫 帥榚丂將 傗側偣 kirkland 摻柤婓朷 俶偲乣 彫妛柤扵掋
傑偲傔
2004擭偺擭偑僗僞乕僩偟偨偐偲巚偭偨傜丄偁偭偲偄偆娫偵傕偆侾儢寧偑夁偓偰偟傑偄傑偟偨丅
崱寧偺栤戣偼丄侾俀亊侾俇俈偺挿曽宍傪偄偐偵彮側偄惓曽宍偱暘妱偱偒傞偐偲偄偆栤戣偱偡丅 傕偪傠傫惓曽宍偺侾曈偺挿偝偼偡傋偰摨偠偱偁傞昁梫偼偁傝傑偣傫丅 僷僘儖偺傛偆側栤戣偱偡偹丅 摎偊偼乽俀侽屄乿偱偡偑丄尩枾偵偄偊偽丄 偙傟偑嵟彫偱偁傞偲偄偆偙偲偺専徹乮徹柧乯偑昁梫偵側傝傑偡丅 壜擻惈偼崅乆桳尷屄偱偡偐傜丄 傕傟偺側偄傛偆偵専徹偟偰偄偗偽偄偄偲巚偄傑偡丅 壗恖偐偺曽偑幚嵺偵専徹偟偰偄偨偩偄偰偄傑偡丅
傎偲傫偳偺曽偑丄嵟屻偵巆偭偨侾俀亊侾侾偺挿曽宍傪偳偆暘偗傞偐偲偄偆傾僾儘乕僠傪偟偰偄傞偺偵懳偟偰丄 A孨偺傾僾儘乕僠偼偪傚偭偲儐僯乕僋偱偡偹丅惓曽宍屄悢偵拲栚傪偟偰丄 侾俀丗侾侾傪幚尰偱偒傞偐丄偲峫偊偰偔傟傑偟偨丅
 E-mail
E-mail
 栠傞
栠傞
 top
top