Weekend Mathematics／問題／問題81

８１．麦わら帽子の問題

ボブとヘレンは、この夏休みメイン州の森で過ごしました。そこにはヘンリー伯父さんの山小屋があるのです。 山小屋まで行くのに、彼らは借りたカヌーをこいで川をのぼっていきました。 ボブが前でオールでこぎ、ヘレンは船尾でこいでいました。２時になったとき、ヘレンは麦わら帽子をぬいで、船尾におきました。 そのとき突風が吹いてきて、ヘレンの帽子は飛ばされてしまいましたが、ヘレンもボブもそれに気がつきませんでした。 上流へ３キロほど離れたとき、はじめてヘレンは気がついて叫びました。

ヘレン　待って！　カヌーを止めて。私のすてきな帽子がなくなっちゃったのよ。

彼らはカヌーの向きを変え、帽子が見つかるまで下流にこいでいきました。 カヌーは時速６キロ（流れのない所で）、そして川が時速２キロで流れていたとすると、 ヘレンが帽子を取り戻したのは何時でしょうか？

答えと解説

解答・その1

（ペンネ−ム：やなせ）

水はあくまでも直線的にまっすぐ、風の抵抗は無い、ボートがＵターンするときの タイムラグはゼロとしますね。 帽子が飛ばされた事に気がついた時にカヌーと帽子の距離が３ｋｍですので そこからＵターンして追いかけるとしたらカヌーの速度から３０分後には 追いつきます。
３ｋｍ÷（６ｋｍ＋２ｋｍ−２ｋｍ）＝０．５時間
３ｋｍ＝バックする時に離れている距離
６ｋｍ＝ボート単独の速度
＋２ｋｍ＝ボートの速度に流れの速度をプラスします
−２ｋｍ＝帽子が流れる速度（川の流れと同じ）

ここで問題は３ｋｍ離れるのに何時間かかるかって事ですよね
ボートが上流に行くときの速度は６ｋｍ−２ｋｍで時速４ｋｍ
帽子は流れと同じで２ｋｍこれから両者が３ｋｍ離れるために必要な時間は
３ｋｍ÷（４ｋｍ＋２ｋｍ）＝０．５時間

カヌーをこぎ始めたのは午後２時（多分午後ですよね。真夜中は怖いもん）にスター トして３０分後に帽子が無くなったのに気がつき、そこから追いつくのに３０分なの で答えは午後３時です。

解答・その2

（ペンネ−ム：Y.M）

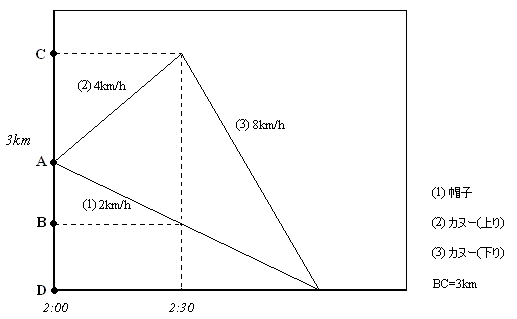
帽子を落とした地点をA、カヌーを引き返したときの帽子の位置をB、カヌーの位置をC、 追いついた地点をDとしておきます。BC=3km
カヌーが引き返したとき、出発から

　　　　3÷(4+2)＝1/2　　　より

30分経過しています。 あとは単純な追いかけですので、

　　　　3÷(8-2)＝1/2　　　より

D地点にて追いつくのは2:30から30分後、即ち 答え、3:00

解答・その3

（ペンネ−ム：aa）

カヌーの速度は時間あたり上り４Ｋｍ、下り８ｋｍ、帽子は２ｋｍです。
ボートと帽子は、時間あたり（４＋２）ｋｍ離れていくので、３ｋｍ離れるには、

　３÷（４＋２）＝0.5時間かかります。

カヌーは時速８ｋｍで、時速２キロで流されていく帽子をおいかけるので、 時間あたり（８−２）＝６ｋｍ近づくことができます。
よって、カヌーが帽子に追いつく時間は、

　３÷６＝0.5時間

です。

以上より、

　帽子が無くなったことに気が付くまでの時間＝0.5時間
　帽子に追いつくまでの時間＝0.5時間

の合計

　１時間

かかります。
よって、ヘレンが帽子を取り戻したのは３時。

解答・その4

（ペンネ−ム：巷の夢）

帽子を落としてからカヌーと帽子の距離が３ｋｍ離れるのは、カヌーの時速 ４ｋｍ、帽子の時速２ｋｍであるから、1/2時間である事が分かる。
因って、帽子を取り戻した時間をXとすると、

　２（X−5/2）＋３　＝　８（X−5/2）　

が成り立つ。これを解いてX＝3を得る。 以上より帽子を取り戻した時刻は３時である。

解答・その5

（ペンネ−ム：杖のおじさん）

カヌーの速度　　　６Kｍ（時速）
落としたと気が付いたときカヌーから帽子までの距離は　　　３Kｍ
としたと思われる時間　　　２時
気づくまでの時間と取りに行く時間は　　　３/６＊２　　　　１時間
拾う時間は　　　２時＋１時間　　　　３時　前後です

前後としたのは拾いに行くためカヌーの向きを変えている間にも帽子は流れていま す。途中で風が渦を巻いているかもしれません、あるときは追い風に、又、あるとは向か い風になるときもあるかもしれません、途中岸とか岩に引っかかっているといいですね！ボッブ！早く 見つけて拾ってあげて下さい。

今回もCASIO(カシオ)　FX―８７０P　 CASIO(カシオ)　FX―８９０P　のポケット コンピューター（ポケコン）でプログラムを作ってみました。

１０　ＰＲＩＮＴ“オトシモノ　ヒロイ”
２０　ＩＮＰＵＴ“フネ　ノ　ハヤサ”，Ａ
３０　ＩＮＰＵＴ“キズイタトキ　ノ　オトシタモノ　カラ　ノキョリ”，Ｂ
４０　ＰＲＩＮＴ“オトシタト　オモワレル　ジカン”
５０　ＩＮＰＵＴ“ジ”，Ｃ，“フン”，Ｄ，“ビョウ”，Ｅ
６０　Ｆ＝ＤＥＧ（Ｃ，Ｄ，Ｅ）　
７０　Ｇ=Ｂ／Ａ＊２：Ｈ＝Ｆ＋Ｇ：Ｉ＄＝ＤＭＳ＄（Ｈ）
８０　ＰＲＩＮＴ　Ｉ＄；“　ゼンゴ　ニ　ミツカリマス”
９０　GOTO　２０

上記プログラム中、 ＤＥＧ（Ｃ，Ｄ，Ｅ）は与えられた６０進数を１０進数に変換する文字関数命令で す。
ＤＭＳ＄（Ｈ）は１０進数を６０進表記の文字列に変換する文字関数命令です。 Ｉ＄は時，分，秒で表示されます。
色々工夫してみてください。さあ！ポケコン持って落し物を拾いに行こう！

解答・その6

（ペンネ−ム：午年のうりぼう）

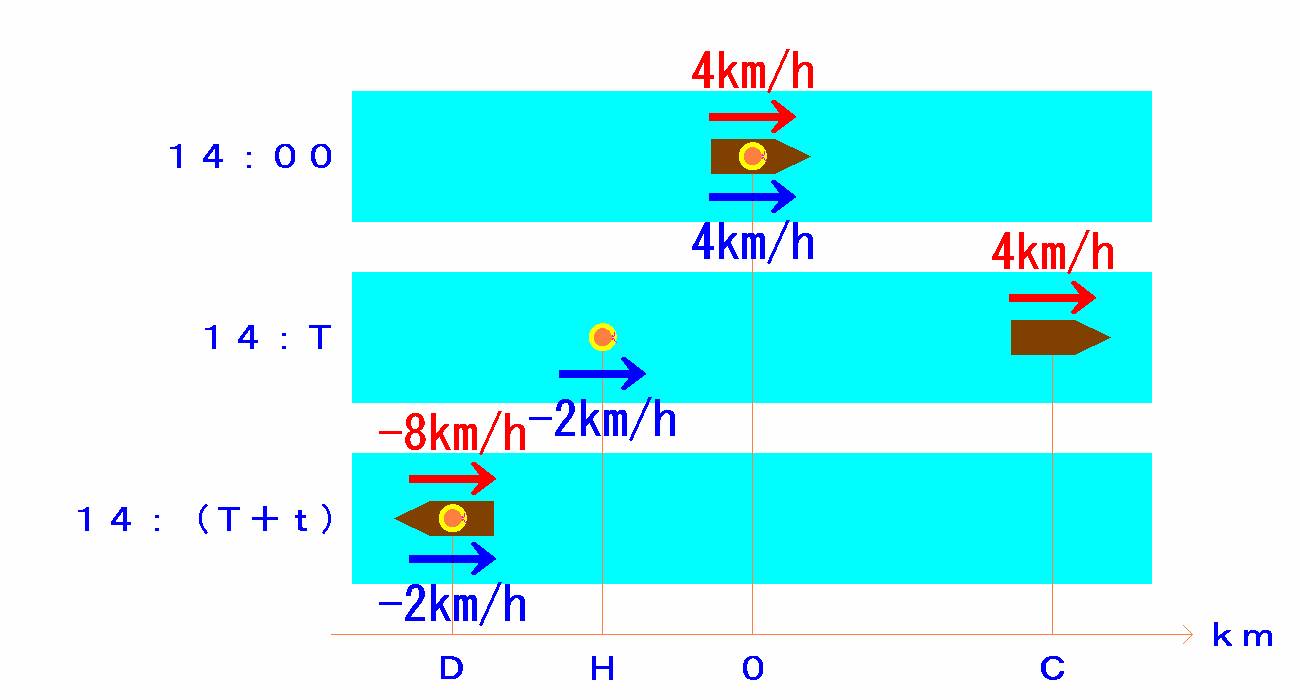
突風が吹いてきて、帽子が飛ばされた地点を０ｋｍ、そのＴ分後の帽子の位置をＨｋｍ、 その時刻のカヌーの位置をＣｋｍ、帽子を取り戻した位置 （この時刻は、帽子が飛ばされてから(Ｔ＋ｔ)分後。）をＤｋｍとする。

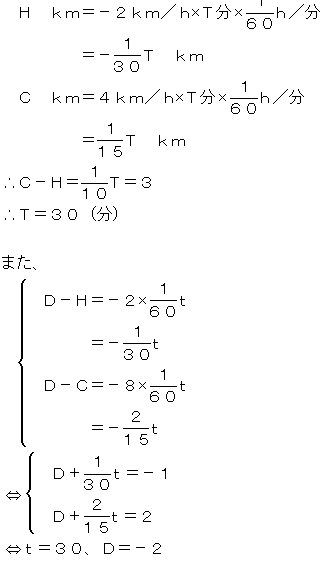
したがって、ヘレンが帽子を取り戻したのは、１４：６０、つまり１５：００である・・・(答)

別解

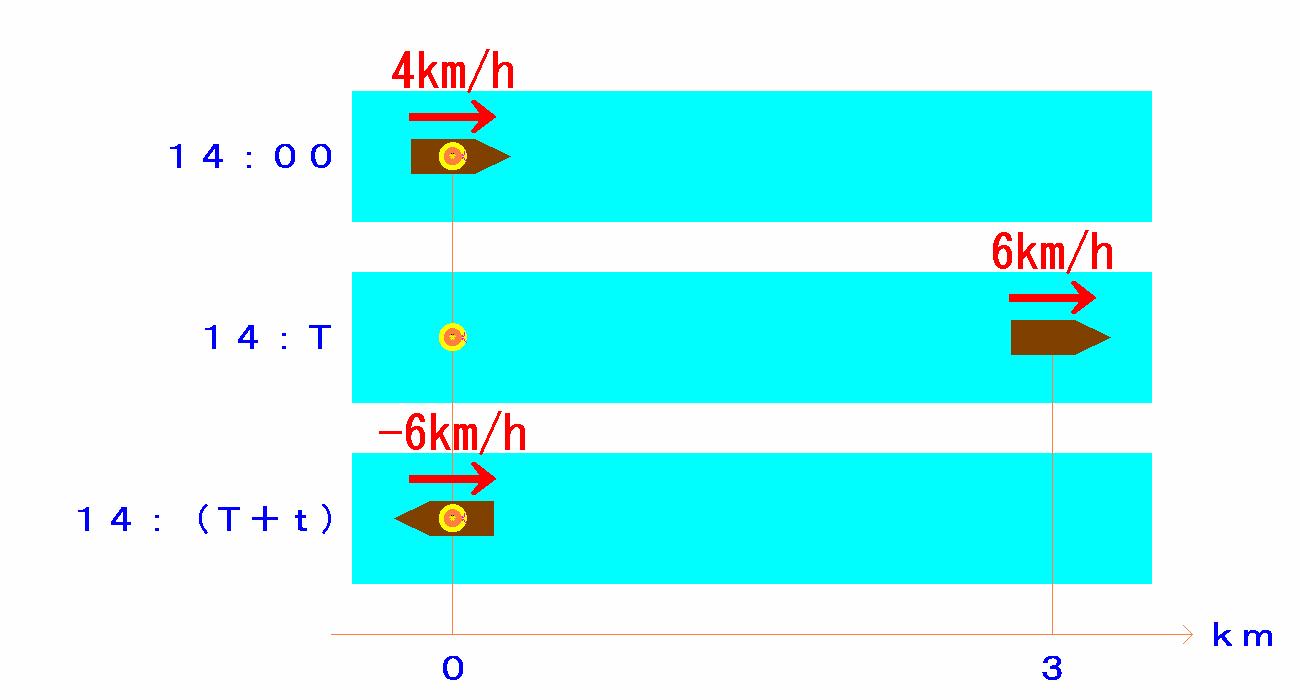
突風が吹いてきて、ヘレンの麦わら帽子が飛ばされ、その麦わら帽子が川の面に落ちたときに、 空からひらひらと一頭のモンキチョウがその帽子の上にひらりととまった。 そこで、このモンキチョウの視点でこの問題を解いていくことにしようと思う。

麦わら帽子の位置を常に０ｋｍ地点とする。

カヌーは、実際は、帽子を落としてからＴ分間は、速度４ｋｍ／ｈで進む。
また、帽子はその間−２ｋｍ／ｈで進む。
そして、帽子を落ちしたことに気づいた地点（位置：３ｋｍ地点、時刻：Ｔ分）から帽子を回収するまでのｔ分間は、 −８ｋｍ／ｈで進む。
また帽子はその間、速度−２ｋｍ／ｈで進む。

だから、モンキチョウは、カヌーの速度は、
　帽子が川に落ちた瞬間（位置：０ｋｍ地点）から、帽子を落としたことに気付く（位置：３ｋｍ地点）まで
　帽子を落としたことに気付いてから帽子を回収する（位置：０ｋｍ地点）までのｔ分間
であると「観測」する。

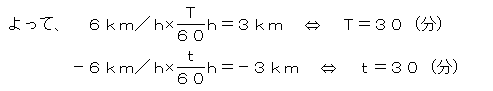
よって、帽子を回収したのは、１４：６０、つまり１５：００である・・・(答)

解答・その7

（ペンネ−ム：Ｎと? ）

水が動いていないと思って問題ないので、３時じゃないすか？ 　でも、３ｋｍではなく、３キロ【ほど】ってのや、船尾とか前とかっ てのも気になりますなぁf(^_^;

解答・その8

（ペンネ−ム：小学名探偵）

答え　3時

川の流れに対するボートの速さ（相対速度）は川を上るときも下るときも時速6ｋｍです。 そこで川に流れがないとして考えますと、静止した麦藁帽子を始点として行きに3ｋｍ、 帰りに3ｋｍ、計6ｋｍ進むのにボートが要する時間は6/6＝1時間です。 麦藁帽子と離れたのが2時なので再会したのは3時です。

解答・その9

（ペンネ−ム：夜ふかしのつらいおじさん）

ヘレンが帽子を取り戻すのは午後３時です。

カヌーは上流に向かうときは (6-2)=4km/h の速さで進み、
下流に向かうときは(6+2)=8km/h の速さで進みます。
帽子は下流に 2km/h の速さで進みます。

カヌーが上流に向かうときは帽子と、１時間に(4+2)=6km ずつ離れていきます。
カヌーが下流に向かうときは帽子に、１時間に(8-2)=6km ずつ近づいていきます。
つまり、この問題を考えるとき、川の流れを考えないで、カヌーの時速６キロだ け考えれば良いのです。

問題の「上流へ３キロほど離れたとき」というのを帽子とカヌーの距離と考える と３キロ離れまたその３キロを追いつくわけですから、合計６キロをカヌーが移 動することを考えればよいので、午後２時から１時間後の３時にヘレンが帽子を 取り戻すと考えられます。

解答・その10

（ペンネ−ム：teki）

答え　　３時ちょうど

＜解法＞
　この種類の問題を「流水算」と呼びますが、ややこしいと感じる のはカヌーの速さと川の流れの速さを両方考えてしまうためです。
　実は、川の流れが一定の場合、カヌーの速さと帽子が流される 速さに両方プラスされるので、この場合は一切考える必要がない のです。
　要するに、静止した水面において、静止している帽子を往復する と考えればいいのです。
　というわけで、片道３ｋｍ（往復６ｋｍ）の距離を時速６ｋｍで往復 するのですから、往復にかかる時間は１時間です。
　帽子が飛ばされたのが２時ちょうどですので、帽子に追いつくの は、それから１時間後の３時ちょうどということになります。

解答・その11

（ペンネ−ム：Toru）

解答：３km離れた時というのがちょっと分かりにくいですが、この時点での帽子とカ ヌーとの距離と考えます。また帽子はその場でポチョンと川に落ちてその後は川の流 れに乗って下流に進むとします。川といっしょに動いている人の視点で考えれば、川 の流れのスピードは場所によらないので、（たとえば川が地球だと考えればよい）、 帽子は止まっていてボートは６km／hrで３km地点までを往復することになり、かかる 時間は１時間で、答は３時。

解答・その12

（ペンネ−ム：yokodon）

細かいことを言えば、帽子が飛んでから着水するまでの時間や、ヘレンが帽子を船 縁においてから帽子が船を離れるまでの時間、及び帽子が空中をとんで着水するまで の水平方向の移動距離、ヘレンが帽子のことに気付いて船が進行方向を変えるまでの 時間が不明ですし、川の形状がどうなっているかも本来なら重要な情報であるはずで すが（きっと、Kirkland さんとこのＡ君当たりは、しっかり気付いているに違いな い）、簡単のため、上記３種の時間は０とし、帽子は船から直下に所要時間０で水面 に落下して以後川の流れる方向に等速運動したものとし、川が直線であるとして、運 動も１次元で考えます。

考えられる場合が２つあるようなので、それぞれに関してコメントします。

場合１：3 km という距離が、帽子が落下した地点からのカヌーの移動距離である場合。

上流に向かうカヌーの速さは 4 km/h 、下流に向かう場合は 8 km/h ですね。
カヌーが上流に 3 km 進む所要時間は 3/4 h（＝45 分）、その間に帽子は落下地 点から 2×3/4 ＝ 1.5 km 下流に移動しています。
そこから t 時間後にカヌーが帽子に追いつくとすると、追いつくまでに必要なカ ヌーの移動距離は 3 + 1.5 + 2t (km) ですから、以下の式が成り立ちます。

　　　　8t ＝ 4.5 + 2t

これを解いて、t ＝ 3/4 (h)（＝ 45 分）を得ます。
合わせて、帽子が追いつくまでの所要時間は、単位を分に換算して 90 分後です。
時刻にして、午後３時30分…（答）、ですかね。

場合２：3 km という距離が、帽子からカヌーまでの距離である場合。

物理の相対速度の考えを用いれば、帽子に対するカヌーの相対速度は、上流に向か う方を速度の正の向きとして、上流に向かう場合が +6 km/h 、下流に向かう場合が -6 km/h で、いずれもその大きさは 6 km/h です。これを用いて考えます。
上流に向かう場合は、帽子とカヌーとの距離が 3 km になるまで離れたわけですか ら、所要時間 t (h) は、

　　　　6t ＝ 3

より t ＝ 1/2 (h)（＝ 30 分）。
ヘレンが帽子のことに気付いてから下流に向かう場合も、3 km の距離を相対速度 のおおきさ 6 km/h で追いかけるわけですから、所要時間 t' (h) は、

　　　　6t ＝ 3

より t' ＝ 1/2 (h)（＝ 30 分）。というわけで、上流に向かう場合と等しくなりま す。
よって、この解釈のもとでは、カヌーが帽子に追いつくのが事件発生後 60 分の時 点、時刻に換算して午後３時ちょうど…（答）、ということになります。

場合１の後半も、相対速度の考え方で出来ますが、前半は無理そうですね。
ただ、いずれにせよ、もうちょっと遅い時刻になりそうな気がしますが。(^^;

解答・その13

（ペンネ−ム：高橋　道広）

帽子にくっついていたアリンコトムは叫びました。
「お〜い　帽子が飛んだよ〜」
ところが先を急いでいたボブとへレンにはその声は届きませんでした だって声も姿も　とってもちいさかったんですもの。 トムからみるとカヌーは時速6kmの速さで遠ざかっていきます。 30分たつと3kmも離れてしまいました。

解１
ようやくカヌーのへレンが気がつきました。 ヘレンたちは帽子のトムからみると時速6kmで近づいてきます。 そして30分後無事にトムと帽子はヘレンの手元に戻ってきたのでした。 それはおやつを食べる午後3時のことでした。めでたし　めでたし

解２
30分こいでもボブは帽子を見つけられませんでした。
「おかしいなあ　もうそろそろ見つかるころなんだけどなあ」
実はボブはとっくに帽子のところについていたのですが、見つけることはできま せんでした。 そう、帽子は水の中を流れていたのです。ボブは帽子が水面に浮いているものだ とばかり思っていたのでした。とうとうへレンの帽子は見つからないで終わった のです。
「まあ　ボブったら　ちっとも役にたたないのねっ」
こうしてボブはヘレンに頭が上がらなくなっていくのでした。ちゃんちゃん

解３
30分こいでもボブは帽子を見つけられませんでした。
「おかしいなあ　もうそろそろ見つかるころなんだけどなあ」
実はボブとヘレンは見過ごしていたのです。こぎ始めて15分たったところで 川が２つに分かれていることを。 だってもうひとつの流れは草に隠れるくらい細い流れだったんですもの。
「まあ　ボブったら　ちっとも役にたたないのねっ」
「もとはとえばヘレンがなくしたんじゃないか」そういう言葉をボブはぐっと 飲み込みました。言い争いになってもどうせ　最後には負けることは火をみるよ り明らかだったからです。 えらいぞボブっ。世の中を知っているっ。 こうしてボブはヘレンに借りをまたひとつつくったのでした。

解４
よくよく読むと帽子が川を流れたとは書いてない。飛ばされて川岸の草に引っか かったかもしれません。
そのときは、3÷(6-2)=3/4時間で気がついて　3÷(6+2)=3/8時間で戻ってきたの で合計　9/8時間後に発見　発見時間は　3時7分30秒のときです。

解答・その14

（ペンネ−ム：kirkland）

Ａ君	「小島先生、お久し振りで〜す。 先月は夏休みだったので、ハワイの別荘でバカンスを楽しんでました！」
先生	「嘘つけ！パソコンが壊れていただけだろ！」
Ａ君	「さて、今月の問題ですが、いろいろと疑問点が残りますね。」
先生	「というと？」
Ａ君	「帽子を置いたのが２時で、 突風が吹いたのも２時だということが分かっていながら、帽子がとばされていることに気 付かないなんて、こいつら大丈夫ですか？」
先生	「そんなことを気にする君こそ大丈夫か？」
Ａ君	「帽子は何ｍぐらい飛ばされたんですかねぇ？ それによって計算が違ってきますし、ひょっとしてずっと空を飛んだま まだと、一生帽子は見つからない！ はたまた、帽子が途中で沈んだりなんかしたりして。さぁヘレン、困っただろ！」
先生	「おいおい、もう気が済んだか？」
Ａ君	「はい、もう充分です。２ヶ月分ボケました。 いやー、ずっとストレスたまってたんですよ。こんな問題、方程式を使 えば一発ですよね！」
先生	「まだボケるつもりか？君は小６なんだから方程式は知らないだろ！」
Ａ君	「一度言ってみたかっただけですよ。 さて、問題文にある『上流へ３ｋｍほど離れた』とあるのは、『突風が吹いた地 点から上流へ３ｋｍ』だと思ったのですが。」
先生	「小島先生からいただいたメールによると、『帽子から上流へ３ｋｍ』ということらしいよ。不自然だとか文句言わな いように！」
Ａ君	「いや、これはごく自然な設定でしょ。 なんてったって、すてきな帽子なんだから、発信器ぐらいついているはずです。 よくスパイ映画なんかで使われているあれですよ。 というわけで、帽子がどこにあるかなんて瞬時に分かるはずですよ。」
先生	「………。まあ、そういうことにしておこうか。 さて、問題を考えていくとしよう。」
Ａ君	「直感なんですが、 カヌーも帽子も川の上にあるんだから、川の流れの速さは無視していいのでは？」
先生	「何故に？」
Ａ君	「これって、新幹線に乗っている人が、 席を立って車内のトイレまで往復するようなもんでしょう。座席が時速200ｋ ｍで進んでいるだなんて、誰も考えないのと同じ理屈だと思います。 というわけで川の流れの速さを無視すると、カ ヌーが３ｋｍを往復するだけなので、６÷６＝１時間後の３時に帽子を取り戻す。 こんな感じでどうでしょう。」
先生	「いいんじゃない。君の言うとおり、川の速さは時速何ｋｍだろうと結果は同じだね。
Ａ君	「先生もまだまだ甘いですね。川の流れの速さが光速と等しい場合は、そんなふうになりませんよ。もう少し物理も勉 強した方がいいんじゃないんですか？」
先生	「あっ、君が理科マニアだという初期の設定を忘れてた……。」

正解者

Toru	高橋　道広	teki
巷の夢	杖のおじさん	Ｎと?
やなせ	夜ふかしのつらいおじさん	aa
Y.M	午年のうりぼう	小学名探偵
kirkland	yokodon

まとめ

今月の楽しい解答、ユニークな解答、どうもありがとうございました。
「上流へ３キロほど離れたとき」という表現が曖昧で大変ご迷惑をおかけしました。 Ａ君にもその不自然さをフォローしていただきましたが・・・、 「帽子から３キロ離れたとき」という解釈でお願いします。
何人かの方にご指摘いただいていますように川の流れ（光速ほどでないならば）は関係ありませんね。 単に帽子とカヌーとの相対的な関係が問題になります。
Ａ君の解答を楽しみにしている読者の方も多いようですので、Ａ君、来月も是非お願いします。 私も楽しみにしています。

E-mail 戻る top