Weekend Mathematics乛栤戣乛栤戣80
俉侽丏崅峑栰媴偺栤戣
崅峑栰媴偺婫愡偵側傝傑偟偨丅崱擭傕抧曽戝夛傪彑偪敳偄偨係俋峑偑慡崙戝夛偵弌応偟傑偡丅 偛懚抦偺捠傝丄僩乕僫儊儞僩曽幃偱桪彑僠乕儉傪寛傔偰偄偒傑偡丅偦偙偱栤戣偱偡丅
(1)帋崌悢偼偄偔偮偱偡偐丠
(2)侾夞愴偐傜弌応偟偨偲偟偰丄壗帋崌彑偰偽桪彑偱偒傑偡偐丠
(3)崅峑栰媴偺僩乕僫儊儞僩偺慻傒曽偼丄壗僠乕儉偐傪侾夞愴柶彍偲偟丄俀夞愴埲崀偼丄敿暘丄敿暘偲側偭偰 寛彑愴偵帄傝傑偡乮侾夞愴挷惍曽幃偲屇傃傑偟傚偆乯丅偙偺応崌丄侾夞愴傪柶彍偝傟傞乮晄愴彑偲側傞乯僠乕儉偼壗僠乕儉偵側傝傑偡偐丠
(4)嵟弶偐傜俀僠乕儉偢偮懳愴偝偣丄敿抂偑偱偨偲偒偩偗侾僠乕儉晄愴彑偲偄偆慻傒曽乮搑拞挷惍曽幃偲屇傃傑偟傚偆乯傪偡傞偲丄帋崌傪柶彍偝傟傞乮晄愴彑偲側傞乯僠乕儉偼偺傋壗僠乕儉偵側傝傑偡偐丠
寖愴嬫恄撧愳戝夛偱偼丄崱擭侾俋俉峑偑弌応偟丄峛巕墍傊偺愗晞傪憟偄傑偟偨丅 摨偠傛偆偵恄撧愳戝夛偺応崌傕峫偊偰傒偰偔偩偝偄丅
乮儁儞僱亅儉丗傗側偣乯
侾乯偱偡偑侾帋崌偱侾僠乕儉偑徚偊傑偡丅係俋僠乕儉嶲壛偱桪彑偡傞偺偼侾僠乕儉偱
偡偐傜
丂丂係俋亅侾亖係俉偱摎偊偼係俉帋崌
俀乯堦夞彑偭偰儀僗僩俁俀丄擇夞彑偭偰儀僗僩侾俇偙偺挷巕偱俉丅係丏俀丆侾偱偡偐
傜彮側偔偰傕俇夞彑偰偽桪彑偱偡偹
俁乯僩乕僫儊儞僩曽幃偺応崌丄偒偭偪傝峴偔側傜俀丏係丏俉丏侾俇丏俁俀丏俇係僠乕
儉嶲壛偱偡偹
偲偙傠偑係俋僠乕儉側偺偱偙傟傪俁俀僠乕儉傑偱偵峣傜側偔偰偼側傝傑偣傫偐傜
係俋亅俁俀亖侾俈偱侾俈帋崌堦夞愴傪峴傢側偗傟偽側傝傑偣傫偺偱丄
帋崌悢偺攞偺僠乕儉偑堦夞愴傪峴傢側偔偰偼側傝傑偣傫丅
偮傑傝俁係僠乕儉偑堦夞愴偵嶲壛巆傝偺侾俆僠乕儉偼柶彍偱偡偹丅
摎偊偼侾俆僠乕儉偱偡丅
係乯堦夞愴偼係俋亐俀亖俀係丒丒丒侾
丂 擇夞愴偼乮俀係亄侾乯亐俀亖侾俀丒丒丒侾
丂 嶰夞愴偼乮侾俀亄侾乯亐俀亖俇丒丒丒侾
丂 巐夞愴偼乮俇亄侾乯亐俀亖俁丒丒丒丒侾
丂 屲夞愴偼乮俁亄侾乯亐俀亖俀丒丒丒丒侽乮徫乯
丂 寛彑愴偼俀亐俀亖侾丒丒丒丒丒侽(敋徫)
偙偺寢壥丄偺傋僠乕儉悢偱偡偺偱奺幃偺梋傝傪崌寁偟偨暔偑摎偊偱偡偹
係僠乕儉偠傖側偄偐側

乮儁儞僱亅儉丗岼偺柌乯
(1) 侾帋崌傗傞偲昁偢侾僠乕儉偑徚偊偰偄偒傑偡丅場偭偰桪彑幰偐傜傒傟偽帺暘埲奜偺係俉僠乕儉偑徚偊偰偔傟傟偽椙偄偺偱丄係俋亅侾亖係俉帋崌
(2) 寛彑偺曽偐傜熻傝丄巆傝偺僠乕儉悢傪峫偊傞偲丄
| 寛彑 | 弨寛彑 | 弨乆寛彑 | 儀僗僩侾俇 | 儀僗僩俁俀 |
|---|---|---|---|---|
| 俀僠乕儉 | 係僠乕儉 | 俉僠乕儉 | 侾俇僠乕儉 | 俁俀僠乕儉 |
(3)崱丄堦夞愴偐傜弌応偡傞僠乕儉悢傪X丄晄愴彑僠乕儉悢傪Y偲偡傞偲丄
丂丂丂X亄Y亖係俋丄乮X/2乯+Y亖俁俀
偺楢棫曽掱幃偑惉棫偡傞丅偙傟傛傝X亖俁係丄Y亖侾俆
懄偪丄媮傔傞晄愴彑僠乕儉悢偼侾俆偱偁傞丅
(4)埲壓偺條偵昞夝偟偰傒傞偲丄丂
| 帋崌 | 嶲壛僠乕儉 | 幚愴僠乕儉 | 晄愴彑僠乕儉 | 彑棙僠乕儉 |
|---|---|---|---|---|
| 堦夞愴 | 係俋 | 係俉 | 侾 | 俀俆 |
| 擇夞愴 | 俀俆 | 俀係 | 侾 | 侾俁 |
| 嶰夞愴 | 侾俁 | 侾俀 | 侾 | 俈 |
| 弨乆寛彑 | 俈 | 俇 | 侾 | 係 |
| 弨寛彑 | 係 | 係 | 侽 | 俀 |
| 寛彑 | 俀 | 俀 | 侽 | 侾 |
亂偍傑偗偺栤戣亃
恄撧愳戝夛傕忋婰偲慡偔摨條偵偟偰
(1) 侾俋俈
(2) 俉
(3) 俆俉
(4) 係丂丂丂弌応僠乕儉悢偵娭學側偔係夞丠寁嶼偟偰傒傑偡丅
巹傕恄撧愳導偵廧傫偱偍傝傑偡偺偱侾俋俉峑偺捀揰偱偁傞墶昹彜戝晅懏崅峑偵偼婃挘偭偰傕傜偄偨偄偟丄僄乕儖傪憲傝傑偡丅

乮儁儞僱亅儉丗宩偍偲偙乯
僩乕僫儊儞僩乮偡側傢偪彑偪敳偒乯曽幃偩偲丄堷偒暘偗偑側偄偐傜帋崌偑偁傟偽昁偢懘偺帋崌偱偺晧偗僠乕儉偑偁傞丄偡側傢偪帋崌偵偼晧偗偨僠乕儉偑侾懳侾偵懳墳偟偰偄傞丅偦傟偱攕戅偡傞僠乕儉悢偼丄弌応慡峑偺拞偐傜桪彑峑傪彍偄偨僠乕儉悢偲側傞丅偡側傢偪丂弌応僠乕儉悢傪俶偲偡傟偽丄俶亅侾偑桪彑僠乕儉偑寛掕偡傞傑偱偺憤帋崌悢偱偡丅
偲偙傠偱丄弌応僠乕儉悢偑俀偺椵忔偺応崌偩偲丂俀値僠乕儉傪堦楍偵暲傋偰抂偐傜俀偮偢偮慻傪嶌偭偰偄偔師偵懘偺彑偪巆偭偨僠乕儉傪丂傑偨抂偐傜弴偵俀偮偢偮慻傪嶌偭偰偄偔丄偙傟傪孞傝曉偟偰偄偔偲嵟屻偵侾僠乕儉偑彑偪巆偭偰桪彑偡傞傑偱堦搙傕丂晄愴彑傪嶌傜傫偱偡傓丅
弌応僠乕儉偑俀偺椵忔偱側偄応崌偵偼晄愴彑傪嶌傞偙偲偵側傞偑丄戞俀夞愴埲崀偵晄愴彑偑弌側偄傛偆偵偡傞偵偼丂戞侾夞愴偱彑偪巆傞僠乕儉悢傪俀偺椵忔偵偡傞昁梫偑偁傞傢偗偱丄偦偙偱弌応僠乕儉悢丂俶丂偵懳偟偰
丂丂俶亜俀値
偱偁傞嵟戝偺俀値傪慖傇偲
丂
丂丂俶亅俀値亖俹
偱俹偑戞侾夞愴帋崌悢偱丄俀値乕俹偑丂戞侾夞愴偺晄愴彑僠乕儉悢偲側傞丅
偱丄戞俀夞愴弌応僠乕儉悢偼丄俹亄俀値乕俹偐傜俀値丂偱偁傝丄
偙偺屻帋崌悢偼丂敿暘丄敿暘偵尭偭偰偄偔偐傜
丂丂戞俀夞愴帋崌悢偼丂丂俀値亅侾
丂丂戞俁夞愴帋崌悢偼丂丂俀値亅俀
丂丂丒丒丒丒丒丒丒丒丒丒丂
偱傕偭偰丂憤帋崌悢丂俽丂偼
丂
| 俽 | 亖俹亄俀値亅侾亄俀値亅俀亄丒丂丒丂丒亄俀亄侾 |
| 亖俶亅俀値亄俀値亅侾亄俀値亅俀亄丒丒丒丒丒亄俀亄侾 丂丂丂丂扐偟丂値亖侽丆侾丆俀丆俁丄丒丒丒丒 |
| 俽 | 亖俶亅俀値亄乮俀値亅侾乯 |
| 亖俶亅侾丂丂丂偲側傞傢偗偱偡丅 |
師偵搑拞挷惍曽幃傪峫偊傞
係俋峑偱奺夞愴偛偲偵丂丂俀偮偢偮慻傪嶌偭偰偄偔偲丂丂帋崌悢偼丄
丂丂戞侾夞愴偼丂丂係俋亐俀亖俀係丂丂丂梋傝侾偑晄愴彑
丂丂戞俀夞愴偼丂丂俀俆亐俀亖侾俀丂丂丂梋傝侾偑晄愴彑
丂丂戞俁夞愴偼丂丂侾俁亐俀亖俇丂丂丂丂梋傝侾偑晄愴彑
丂丂戞係夞愴偼丂丂7亐俀亖丂俁丂丂丂丂梋傝侾偑晄愴彑
丂丂戞俆夞愴偼丂丂係亐俀亖俀
丂丂戞俇夞愴偼丂丂俀亐俀亖侾
偲側偭偰丂晄愴彑偼崌寁係偱丂丂墑傋係僠乕儉偑柶彍偝傟傞傢偗偱偡丅
摨條偵丂侾俋俉峑弌応偺恄撧愳戝夛傪峫偊偰傒傞偲
侾俋俉亅侾亖侾俋俈
侾俋俉亜俀値丂丂丂丂丂丂丂値亖俈偱丂丂俀俈亖侾俀俉
侾俋俉亅侾俀俉亖俈侽丂丂丂丂丂丂丂侾俀俉亅俈侽亖俆俉
俽亖俈侽亄俀俇亄俀俆亄俀係亄俀俁亄俀俀亄俀侾亄俀侽傛傝丂戞俉夞愴傑偱偁傞偐傜丄俉夞彑偭偰桪彑
偦偟偰丂俆俉偑晄愴彑僠乕儉悢偱偡側
師偵搑拞挷惍曽幃偱偼
丂丂侾俋俉亐俀亖俋俋
丂丂俋俋亐俀亖係俋丂亄晄愴彑丂侾
丂丂俆侽亐俀亖俀俆
丂丂俀俆亐俀亖侾俀丂亄晄愴彑丂侾
丂丂侾俁亐俀亖俇丂丂亄晄愴彑丂侾
丂丂俈亐俀丂亖俁丂丂亄晄愴彑丂侾
丂丂係亐俀亖俀
丂俀亐俀亖丂侾丂丂丂丂丂丂偲側偭偰晄愴彑悢偼丂傗偭傁傝丂係
丂丂

乮儁儞僱亅儉丗儕僫儔僀乯
夝摎乮1乯丗偙傟偼丄慡晹偺帋崌悢傪尵偊偽椙偄偺偱偡傛偹?
1帋崌廔傢傞枅偵1僠乕儉攕戅偟丄嵟廔揑偵偼1僠乕儉偑桪彑偡傞偺偱丄弌応僠乕儉悢-1帋崌偁傝傑偡
49-1亖48帋崌
恄撧愳丗198-1亖197
乮2乯丗堦夞愴廔傢傞枅偵僠乕儉偑敿暘偵尭傝傑偡
傛偭偰丄26亜49亜25側偺偱丄6帋崌彑偰偽桪彑偱偒傑偡
恄撧愳丗28亜198亜27側偺偱丄8帋崌彑偰偽桪彑偱偒傑偡
乮3乯丗2n偵偡傟偽丄偦偺偁偲敿抂側偔帋崌偑恑傓偺偱
乮2乯傛傝49偐傜25亖32偵偡傞偵偼17峑偑攕戅偟側偗傟偽偄偗傑偣傫
側偺偱丄34僠乕儉偑嶲壛偡傟偽偄偄傢偗偱偡偐傜49-34亖15僠乕儉偑堦夞愴晄愴彑偵側傝傑偡
恄撧愳丗乮2乯傛傝198偐傜27亖128偵偡傞偵偼70僠乕儉偑攕戅偟側偗傟偽偄偗傑偣傫
側偺偱丄140僠乕儉偑嶲壛偡傟偽椙偄傢偗偱偡偐傜198-140亖58僠乕儉偑堦夞愴晄愴彑偵側傝傑偡
乮4乯丗曽朄傛傝2偱妱傝偮偯偗偰婏悢偵側偭偨帪偵-1偟偰嵟廔揑偵1偵偡傟偽偄偄
偙偺応崌丄-1偟偨応崌偼妱偭偨屻偵+1偟側偗傟偽側傝傑偣傫
晄愴彑偼丄堦僠乕儉堦夞傑偱偲偟偨帪丄-1偟偨夞悢亖晄愴彑偵側偭偨僠乕儉悢偲側傝傑偡
49佀25佀13佀7佀4仺2仺1乮佀偺帪-1偟偨偲偡傞乯
4夞敿抂偑弌偨偺偱丄4僠乕儉偑晄愴彑偲側傝傑偟偨
恄撧愳丗198仺99佀45佀23佀12仺6仺3佀2仺1
4夞敿抂偑弌偨偺偱丄4僠乕儉偑晄愴彑偲側傝傑偟偨

乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
係俋峑偺応崌
乮侾乯係俉帋崌偱偡丅
僩乕僫儊儞僩曽幃偺応崌丄嵟屻傑偱晧偗側偄僠乕儉偑侾偮巆傝傑偡丅帋崌悢偼 懠偺僠乕儉偑侾夞偢偮晧偗傞夞悢偲側傝傑偡丅偮傑傝嶲壛僠乕儉悢偐傜侾傪堷偄 偨悢偱偡丅
寛彑愴偐傜侾夞愴偵偝偐偺傏偭偰偄偔偲丄僠乕儉悢偑攞乆偵憹偊傑偡丅僠乕儉 悢偼丄弶崁侾丄岞斾俀偺摍斾悢楍偵側傞偺偱乷侾丆俀丆係丆俉丆侾俇丆俁俀丆俇 係丆侾俀俉丆俀俆俇丆丒丒丒乸偲側傝傑偡丅桪彑偵昁梫側彑棙悢偼丄崁偺娫偺僇 儞儅乭丆乭傪悢偊偰偄偒弶傔偰嶲壛僠乕儉傪墇偊傞偲偒偱偡丅
侾夞愴挷惍曽幃偱侾夞愴傪柶彍偝傟傞僠乕儉偼丄乮俀乯偺摍斾悢楍偱僠乕儉悢 傪墇偊傞嵟彫偺崁偐傜嶲壛僠乕儉悢傪堷偄偨抣偱偡丅偮傑傝俇係亅係俋亖侾俆偱 偡丅巆傝偺係俋亅侾俆亖俁係僠乕儉偼侾夞愴傪愴偭偰敿悢偺俁係亐俀亖侾俈僠乕 儉偲側傝傑偡丅侾夞愴柶彍偺侾俆僠乕儉偲侾夞愴傪彑偪忋偑偭偨侾俆亄侾俈亖俁 俀僠乕儉偱俀夞愴傪峴偄傑偡丅
嶲壛僠乕儉悢傪俀偱妱偭偰偄偔偲偒梋傝偑弌偨夞悢偑帋崌傪柶彍偝傟傞夞悢偱 偡丅彜偲梋傝傪壛偊偰偙偺寁嶼傪孞傝曉偟偰偄偒嵟屻偵彜偑侾偵側傞傑偱偵梋傝 偑壗夞弌偨偐傪悢偊傑偡丅
丂侾夞愴丗係俋亐俀亖俀係丒丒丒侾丂丂俀夞愴丗俀俆亐俀亖侾俀丒丒丒侾
丂俁夞愴丗侾俁亐俀亖丂俇丒丒丒侾丂丂係夞愴丗丂俈亐俀亖丂俁丒丒丒侾
丂俆夞愴丗丂係亐俀亖丂俀丂丂丂丂丂丂俇夞愴丗丂俀亐俀亖丂侾
侾俋俉峑偺応崌
乮侾乯侾俋俈帋崌偱偡丅
乮俀乯俉帋崌偱偡丅
乮俁乯俀俆俇亅侾俋俉亖俆俉僠乕儉偱偡丅
乮係乯係僠乕儉偱偡丅
丂侾夞愴丗侾俋俉亐俀亖俋俋丂丂俀夞愴丗俋俋亐俀亖係俋丒丒丒侾
丂俁夞愴丗丂俆侽亐俀亖俀俆丂丂係夞愴丗俀俆亐俀亖侾俀丒丒丒侾
丂俆夞愴埲崀偼係俋峑偺応崌偲摨偠側偺偱丄偁偲俀僠乕儉憹偊傞偙偲偑暘偐傝傑 偡丅

乮儁儞僱亅儉丗Y.M乯
(1)
1帋崌偡傞偛偲偵1僠乕儉晧偗偰偄偔傢偗偱偁傝丄
嵟屻偵巆偭偨1僠乕儉偑桪彑偡傞偺偱丄
丂丂丂49-1=48
Ans.48帋崌
(2)
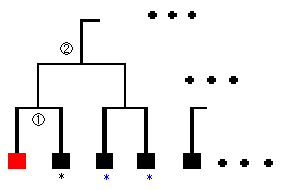
帺暘丗愒偲偟傑偡丅丂彑偪恑傓偺偼丄帺暘偺僠乕儉偱偡丅
嘆仺2僠乕儉偺偆偪丄1僠乕儉彑偪忋偑傞丅
嘇仺忋偵忋偑傟傞偺偼4僠乕儉偺偆偪1僠乕儉丅
嘊偱偼8僠乕儉拞1僠乕儉丅嘋偱偼16僠乕儉拞1僠乕儉丅丒丒丒偲傗偭偰偄偗偽丄
嘍偱偼32僠乕儉拞1僠乕儉丅(32<49)
嘐偱偼64僠乕儉拞1僠乕儉丅(49<64)
懄偪丄5帋崌偱偼桪彑偵偼晄廫暘丄6帋崌栚傑偱彑偪懕偗傟偽椙偄偲偄偆偙偲偵側傝傑偡丅
Ans.6帋崌
(3)
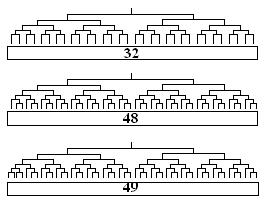
桪彑偺1僠乕儉偐傜弴偵憹傗偟偰偄偒傑偡丅
扨弮偵2攞丄2攞偟偰偄偭偰嵟戝32僠乕儉丅
1夞愴偺2僠乕儉偺偆偪1僠乕儉傪僔乕僪偝偣偰48僠乕儉丅
1僠乕儉暘傪偳偙偐偵曗偄49僠乕儉丅
偙偺偲偒1夞愴柶彍偺僠乕儉偼丄15僠乕儉丅
Ans.15僠乕儉
(4)
32僠乕儉偼姰慡偵抂悢傪弌偡偙偲側偔愴偊傞偺偱丄
巆傝17僠乕儉偱峫偊偰傒傑偟偨丅
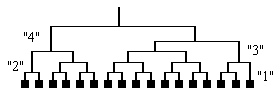
傛偭偰偺傋4僠乕儉
Ans.4僠乕儉

乮儁儞僱亅儉丗奰杮丂峗乯
亙働乕僗侾丗峛巕墍係俋僠乕儉偺応崌亜
侾丏
乬僩乕僫儊儞僩宍幃乭偺婎杮揑側塣梡偵偮偄偰峫偊偰傒傞偲
乽僌僗儞(T_T)丅偆偪偺妛峑丄帋崌偟偰側偄偺偵扙棊偟偪傖偭偨傛丅乿
亀偍偄偍偄偦傫側僴僘側偄偩傠丅帋崌偱晧偗側偄尷傝扙棊偼側偄傛丅亁
乽崱擔偺帋崌偼晧偗偪傖偭偨偗偳丄傑偨柧擔婃挘傟偽偄偄傛偹丅乿
亀偍偄偍偄壗尵偭偰傫偩傛丅晧偗偨傜偦偙偱偍偟傑偄偠傖傫偐丅亁
偮傑傝偼
丂丂乬侾帋崌峴傢傟傞枅偵侾僠乕儉偢偮扙棊偟偰偄偔乭
丂丂乬偁傞侾僠乕儉埲奜偺慡偰偺僠乕儉偑扙棊偡傞偲桪彑僠乕儉偑寛傑傞乭
偲峫偊傜傟傞偺偱
丂丂憤帋崌悢亖憤僠乕儉悢亅侾丂偲尒側偣傞丅
峛巕墍偱偺僶僩儖偼傕偪傠傫係俉帋崌峴傢傟偨帪揰偱係俉僠乕儉偑扙棊偟
嵟屻偵巆偭偨侾僠乕儉偑桪彑偲側傞帠偑暘偐傞丅
俀丏
偙傟偵娭偟偰偼丄帋崌悢偺挷惍曽幃丄晄愴彑偺埖偄偵傛偭偰
曄傢偭偰偔傞偐傕偟傟傑偣傫偺偱愭偵俁斣丄係斣傪夝偄偪傖偄傑偟傚偆丅
俁丏
寛彑偵巆傞偺偼俀僠乕儉丄弨寛彑偵巆傞偺偼偦偺俀攞偱係僠乕儉
弨乆寛彑偵巆傞偺偼峏偵偦偺俀攞偱俉僠乕儉丒丒丒
偲峫偊偰偄偔偲丄僠乕儉悢偑俀偺値忔乮値偼帺慠悢乯偱偁偭偨応崌
晄愴彑偵傛傞帋崌悢偺挷惍傪峴偆昁梫偑側偄帠偑暘偐傞丅
偲側傞偲丄嵟弶偵偄傞偺偑係俋僠乕儉偩偐傜
係俋埲壓偱俀偺値忔偲側傞嵟戝偺悢帤偼丒丒丒俀俆亖俁俀偱偁傞帠偑暘偐傝
侾帋崌栚偑廔傢偭偨帪揰偱俁俀僠乕儉巆偭偰偄傟偽
偦傟埲崀偼晄愴彑偵傛傞挷惍偺昁梫偑側偄帠偑暘偐傞丅
偙偙偱栤侾偺夝摎偺乽帋崌悢亖尭傞僠乕儉悢乿傪巚偄弌偡偲
侾夞愴偱侾俈帋崌峴傢傟傟偽丄係俋亅侾俈亖俁俀偱
俀夞愴偵偪傚偆偳俁俀僠乕儉巆傞帠偑暘偐傝
侾俈帋崌峴偆丂仺丂侾俈亊俀亖俁係僠乕儉偑帋崌傪峴偆帠偑暘偐傝
侾夞愴偱晄愴彑偲側傞僠乕儉悢偼係俋亅俁係亖侾俆僠乕儉偱偁傞帠偑暘偐傞丅
係丏
尰嵼巆偭偰偄傞僠乕儉悢傪傕偲偵
師偺帋崌悢丄晄愴彑僠乕儉悢丄帋崌寢壥偺巆傝僠乕儉悢傪峫偊傞偲
亂尰嵼偺僠乕儉悢偑嬼悢偱偁偭偨応崌亃
師偺帋崌悢亖尰嵼偺僠乕儉悢亐俀
晄愴彑僠乕儉悢亖侽
帋崌寢壥巆傝僠乕儉悢亖尰嵼偺僠乕儉悢亅師偺帋崌悢亖尰嵼偺僠乕儉悢亐俀
亂尰嵼偺僠乕儉悢偑婏悢偱偁偭偨応崌亃
師偺帋崌悢亖乮尰嵼偺僠乕儉悢亅侾乯亐俀
晄愴彑僠乕儉悢亖侾
帋崌寢壥巆傝僠乕儉悢亖尰嵼偺僠乕儉悢亅師偺帋崌悢
偲側傞帠偑暘偐傞偺偱丄係俋傪偙偺婯懃偵摉偰偼傔偰寁嶼偡傞偲
| 丂 | 帋崌悢 | 晄愴彑悢 | 巆傝僠乕儉悢 |
|---|---|---|---|
| 侾夞愴 | 俀係 | 侾 | 俀俆 |
| 俀夞愴 | 侾俀 | 侾 | 侾俁 |
| 俁夞愴 | 俇 | 侾 | 俈 |
| 係夞愴 | 俁 | 侾 | 係 |
| 俆夞愴 | 俀 | 侽 | 俀 |
| 俇夞愴 | 侾 | 侽 | 侾 |
偙偙偱栤俀偵栠偭偰峫偊偰尒傞偲丄栤俁偺儖乕儖偱峴偭偨応崌偼
| 丂 | 帋崌悢 | 晄愴彑悢 | 巆傝僠乕儉悢 |
|---|---|---|---|
| 侾夞愴 | 侾俈 | 侾俆 | 俁俀 |
| 俀夞愴 | 侾俇 | 侽 | 侾俇 |
| 俁夞愴 | 俉 | 侽 | 俉 |
| 係夞愴 | 係 | 侽 | 係 |
| 俆夞愴 | 俀 | 侽 | 俀 |
| 俇夞愴 | 侾 | 侽 | 侾 |
偟偐偟丄栤係偺儖乕儖偱帋崌傪峴偭偨応崌偼
| 丂 | 帋崌悢 | 晄愴彑悢 | 巆傝僠乕儉悢 |
|---|---|---|---|
| 侾夞愴 | 俀係 | 侾 | 俀俆 |
| 俀夞愴 | 侾俀 | 侾 | 侾俁 |
| 俁夞愴 | 俇 | 侾 | 俈 |
| 係夞愴 | 俁 | 侾 | 係 |
| 俆夞愴 | 俀 | 侽 | 俀 |
| 俇夞愴 | 侾 | 侽 | 侾 |
亙働乕僗俀丗恄撧愳戝夛侾俋俉僠乕儉偺応崌亜
侾丏
偙傟偼峛巕墍偺働乕僗偲摨條偵峫偊傜傟丄侾俋俈帋崌偲側傞丅
俁丏
侾俋俉埲壓偱俀偺値忔偲側傞嵟彫偺抣偼丂俀俈亖侾俀俉
偡側傢偪丄侾帋崌栚偑廔傢偭偨帪揰偱侾俀俉僠乕儉巆偭偰偄傟偽椙偄偺偱
侾俋俉亅侾俀俉亖俈侽丂偱丄侾夞愴偱俈侽帋崌偑峴傢傟傟偽乮亖侾係侽僠乕儉偑愴偊
偽乯偪傚偆偳俀夞愴偱偼侾俀俉僠乕儉巆傞偺偱
侾俋俉亅侾係侽亖俆俉丂偱俆俉僠乕儉偑侾夞愴偱晄愴彑偲側傞丅
係丏
峛巕墍偺働乕僗偲摨條偵峫偊傞偲
| 丂 | 帋崌悢 | 晄愴彑悢 | 巆傝僠乕儉悢 |
|---|---|---|---|
| 侾夞愴 | 俋俋 | 侽 | 俋俋 |
| 俀夞愴 | 係俋 | 侾 | 俆侽 |
| 俁夞愴 | 俀俆 | 侽 | 俀俆 |
| 係夞愴 | 侾俀 | 侾 | 侾俁 |
| 俆夞愴 | 俇 | 侾 | 俈 |
| 俇夞愴 | 俁 | 侾 | 係 |
| 俈夞愴 | 俀 | 侽 | 俀 |
| 俉夞愴 | 侾 | 侽 | 侾 |
俀丏
侾夞愴挷惍曽幃偺応崌偼
| 丂 | 帋崌悢 | 晄愴彑悢 | 巆傝僠乕儉悢 |
|---|---|---|---|
| 侾夞愴 | 俈侽 | 俆俉 | 侾俀俉 |
| 俀夞愴 | 俇係 | 侽 | 俇係 |
| 俁夞愴 | 俁俀 | 侽 | 俁俀 |
| 係夞愴 | 侾俇 | 侽 | 侾俇 |
| 俆夞愴 | 俉 | 侽 | 俉 |
| 俇夞愴 | 係 | 侽 | 係 |
| 俈夞愴 | 俀 | 侽 | 俀 |
| 俉夞愴 | 侾 | 侽 | 侾 |
搑拞挷惍曽幃偺応崌偼
| 丂 | 帋崌悢 | 晄愴彑悢 | 巆傝僠乕儉悢 |
|---|---|---|---|
| 侾夞愴 | 俋俋 | 侽 | 俋俋 |
| 俀夞愴 | 係俋 | 侾 | 俆侽 |
| 俁夞愴 | 俀俆 | 侽 | 俀俆 |
| 係夞愴 | 侾俀 | 侾 | 侾俁 |
| 俆夞愴 | 俇 | 侾 | 俈 |
| 俇夞愴 | 俁 | 侾 | 係 |
| 俈夞愴 | 俀 | 侽 | 俀 |
| 俉夞愴 | 侾 | 侽 | 侾 |

乮儁儞僱亅儉丗aa乯
乮1乯(堷偒暘偗嵞帋崌偑側偄応崌乯侾帋崌峴偆偲丄侾峑偑攕戅偟傑偡丅
48峑攕戅偡傞偲丄巆偭偨侾峑偑桪彑偱偡丅
偱丄摎偊偼丄堷偒暘偗嵞帋崌側偳偑側偄応崌偼丄48帋崌丅
乮2乯
(I)夞愴悢傪嵟彫偵偡傞慻傒崌傢偣
偙傟偼丄僔乕僪峑傪嬌椡彮側偔偡傞偙偲丅
嵟屻偺侾峑乮桪彑峑乯傪寛傔傞偨傔偵偼丄俀峑偵傛傞愴偄偑昁梫丅
俀峑偺愴偄偺偨傔偵偼丄係峑偵傛傞帋崌偑昁梫偲偄偆傛偆偵峫偊偰丄
嶲壛偱偒傞峑悢偼丄侾亅俀亅係亅俉亅侾俇亅俁俀亅俇係偲側傞偐傜丄
俇夞帋崌彑偰偽桪彑偱偒傞丅
(II)夞愴悢傪嵟戝偵偡傞慻傒崌傢偣
僔乕僪峑傪嵟戝偵偡傞偲丄
-----+ 丂 +---+ -----+ +---+ ---------+ +---+ -------------+ +--- -----------------+
乮3乯侾夞愴偑廔傢偭偨抜奒偱俁俀峑偑巆偭偰偄傞忬懺偵偟偨偄偐傜丄 侾夞愴偱係俋亅俁俀亖侾俈峑傪攕戅偝偣傞昁梫偑偁傞丅 侾俈峑攕戅偺偨傔偵偼丄俁係峑偵傛傞帋崌偑昁梫側偺偱丄侾夞愴柶彍偼丄 係俋亅俁係亖侾俆峑丅
乮4乯幚嵺偵寁嶼偟偰傒傞偲丄
| n夞愴 | 慡懱偺僠乕儉悢 | 晄愴彑 | 彑偪巆偭偨僠乕儉悢 |
|---|---|---|---|
| 侾 | 係俋 | 侾 | 俀係 |
| 俀 | 俀俆 | 侾 | 侾俀 |
| 俁 | 侾俁 | 侾 | 俇 |
| 係 | 俈 | 侾 | 俁 |
| 俆 | 係 | 侽 | 俀 |
| 俇 | 俀 | 侽 | 侾 |

乮儁儞僱亅儉丗忨偺偍偠偝傫乯
崅峑栰媴係俋峑偺応崌
丂乮侾乯 帋崌悢偼丂丂丂丂丂丂丂丂丂丂係俋亅侾亖係俉丂丂丂係俉帋崌偱偡
丂乮俀乯 侾夞愴偐傜弌偰壗帋崌彑偰偽桪彑偐丂丂丂丂丂丂丂丂6彑偱偡
丂乮俁乯 晄愴彑偼丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂侾俆僠乕儉偱偡
丂乮係乯 搑拞挷惍曽幃丂丂晄愴彑偲側傞僠乕儉悢偼丂丂係僠乕儉偱偡
恄撧愳戝夛侾俋俉峑偺応崌
丂乮侾乯 帋崌悢偼丂丂丂丂丂侾俋俉亅侾亖侾俋俈丂丂丂丂丂侾俋俈帋崌偱偡
丂乮俀乯 侾夞愴偐傜弌偰壗帋崌彑偰偽桪彑偐丂丂丂丂丂丂丂俉彑偱偡
丂乮俁乯 晄愴彑偼丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俆俉僠乕儉偱偡
丂乮係乯 搑拞挷惍曽幃丂丂晄愴彑偲側傞僠乕儉悢偼丂丂係帋崌偱偡
崱夞傕CASIO乮僇僔僆乯丂FX乗俉俈侽P丂 CASIO乮僇僔僆乯丂FX乗俉俋侽P丂偺億僢
働僩僐儞僺儏乕僞乕乮億働僐儞乯偱僾儘僌儔儉傪嶌傝挷傋傑偟偨丅
僾儘僌儔儉偼師偺捠傝偱偡
侾侽丂INPUT乬僩僠儏僂僠儑僂僙僀乕侾丆僩乕僫儊儞僩乕俀乭丟M 俀侽丂IF丂M=1丂THEN丂侾俀侽 俁侽丂INPUT乬僠乕儉丂僗僂乭丟A 係侽丂FOR丂L=1丂TO丂侾侽 俆侽丂IF丂俀丱L亖亜A丂THEN丂俈侽 俇侽丂NEXT丂L 俈侽丂PRINT乬僔傾僀丂僗僂乭丟A-1 俉侽丂PRINT乬僼僙儞僔儑僂僠乕儉僗僂乭丟俀丱L亅A 俋侽丂PRINT乭儐僂僔儑儅僨僲丂僔傾僀僗僂乭丟L 侾侽侽丂IF丂INKEY$=乬乭丂THEN丂侾侽侽 侾侾侽丂GOTO俁侽 侾俀侽丂PRINT乬僩僠儏僂僠儑僂僙僀乭 侾俁侽丂D=侽丗C=侽丗B=侽丗INPUT乬僠乕儉丂僗僂乭丟俙 侾係侽丂IF丂俙亖侾丂俿俫俤俶丂俹俼俬俶俿乬僀儗僫僆僔僥僋僟僒僀乭丗俧俷俿俷丂侾俁侽 侾俆侽丂B=A 侾俇侽丂IF丂B亖亙侾丂俿俫俤俶丂俹俼俬俶俿乬儐僂僔儑僂儅僨乭丟D丟乬僔傾僀乕僼僙儞僔儑僂僠乕儉僗僂乭丟C 丂丂丂丂丗俧俷俿俷丂侾俁侽 侾俈侽丂PRINT丂B丟 侾俉侽丂IF丂FRAC(B乛俀)亜侽丂俿俫俤俶丂俛亖俬俶俿乮亅乮俛乛俀乯仏乮亅侾乯丗 丂丂丂丂俠亖俠亄侾丗俢亖俢亄侾丗GOTO丂俀侽侽 侾俋侽丂俛亖俛乛俀丗俢亖俢亄侾 俀侽侽丂GOTO丂侾俇侽
EXE傪墴偡偲丂僠乕儉丂僗僂丠丂偲暦偄偰偒傑偡偺偱丂恄撧愳戝夛偺応崌側偺偱侾俋俉
偲擖椡偟傑偡
弖帪偵摎偊偑師偺傛偆偵弌傑偡丅
丂丂丂丂僔傾僀丂僗僂丂丂 丂侾俋俈
丂丂丂丂僼僙儞僔儑僂僠乕儉僗僂丂丂俆俉
丂丂丂丂儐僂僔儑僂儅僨丂僲丂僔傾僀僗僂丂 丂俉
師偵嵟弶偐傜俀僠乕儉傪慻傓偲偳偺傛偆偵側傞偐挷傋傑偡
僩僠儏僂僠儑僂僙僀乕侾丆僩乕僫儊儞僩乕俀丂偲丂暦偄偰偒傑偡偺偱侾偲擖椡偟偰
EXE丂傪墴偟幚峴偟傑偡丅
僠乕儉丂僗僂丠丂偲暦偄偰偒傑偡偺偱丂崅峑偺応崌側偺偱丂係俋丂偲擖椡偟傑偡丅
弖帪偵摎偊偑師偺傛偆偵弌傑偡丅
係俋丂俀俆丂侾俁丂俈丂係丂俀丂丂丂儐僂僔儑僂儅僨俇僔傾僀乕僼僙儞僔儑僂僠乕儉
僗僂係丂偲昞帵偝傟傑偡
僠乕儉丂僗僂丠丂偲暦偄偰偒傑偡偺偱丂恄撧愳戝夛偺応崌側偺偱丂侾俋俉丂偲擖椡
偟傑偡丅
弖帪偵摎偊偑師偺傛偆偵弌傑偡丅
侾俋俋丂俋俋丂俆侽丂俀俆丂侾俁丂俈丂係丂俀丂儐僂僔儑僂儅僨俉僔傾僀乕僼僙儞
僔儑僂僠乕儉僗僂係丂偲昞帵偝傟傑偡
僾儘僌儔儉拞侾俉侽峴偺FRAC偼彫悢揰埲壓偺抣傪曉偡娭悢偱偡丅
偟偨偑偭偰丂丂丂丂丂丂FRAC乮B乛俀乯偲丂B乛俀亅俬俶俿乮俛乛俀乯偼摨偠抣偑弌傑
偡
彫悢揰埲壓偑偁傞偐丄偳偆偐偱婏悢丄嬼悢偺敾抐傪偟偰偄傑偡丅
MOD娭悢偼僄僋僙儖偵偁傝傑偡偑妱傝嶼偺梋傝傪弌偟傑偡丅俀偱妱傞偺偱梋傝偑偁傞
偙偲偼婏悢偲敾抐偟傑偡丅
僄僋僙儖偺儐乕僓乕僼僅乕儉偱僾儘僌儔儉傪嶌傞応崌偼B乛俀亅俬俶俿乮俛乛俀乯傪
巊偆偺偑椙偄偱偟傚偆丅
俬俶俹倀俿偼Val(TextBox1.Text)偱擖椡偟俹俼俬俶俿偼Label1.Caption
偱弌椡偟傑偡乮VisualBasic偱偼 TextBox1.Text 偼Text1.text 偲側傝傑偡乯
偙偺僾儘僌儔儉傪CommandButton侾偺僐乕僪偵婰弎偟幚峴偟傑偡
崱偼丄NEC丂PC乕8201乮僴儞僪僿儖僪僐儞僺儏乕僞乯傕憤摦堳偟偰栤戣偵庢傝慻傫偱
偄傑偡丅

乮儁儞僱亅儉丗teki乯
乮侾乯丂係俉帋崌
乮俀乯丂俇帋崌
乮俁乯丂侾俆僠乕儉
乮係乯丂係僠乕儉
亙峫偊曽亜
乮侾乯偼挻桳柤側栤戣偱丄侾帋崌峴偆搙偵侾僠乕儉偑晧偗偰徚偊傞偺偱丄桪彑僠乕儉
傪彍偄偰丄昁偢侾偮晧偗傞偙偲偵側傝傑偡丅
傛偭偰丄帋崌悢偼丄嶲壛僠乕儉悢亅侾偲側傝傑偡丅
乮俀乯偼丄係俋僠乕儉偱僩乕僫儊儞僩傪峴偭偨応崌丄侾夞愴偐傜偺嶲壛偩偲丄俀俇亖俇係
側偺偱俇帋崌峴偆偙偲偵側傝傑偡丅
堦斒揑偵偼丄嶲壛僠乕儉悢傪N偲偡傞偲丄俀値-侾亙N亖亙俀値偲側傞値偑帋崌悢偱偡丅
乮俁乯偼丄侾夞愴廔椆帪偵俁俀僠乕儉偑巆傞傛偆側慻崌偣偲側傞偺偱丄俇係亅係俋亖侾俆
僠乕儉偑侾夞愴晄愴彑偲側傝傑偡丅
乮媡偺峫偊曽偱尵偆偲丄侾夞愴傪慡偰峴偆偺偵昁梫側僠乕儉悢偼俇係偱偡偺偱丄壦嬻
偺侾夞愴傪峴偭偨帪偺壦嬻偺侾夞愴嶲壛僠乕儉悢偲傕尵偊傑偡丅乯
乮係乯偼丄係俋僠乕儉偱幚巤偟偨応崌丄嵟弶偵侾丄師偵侾丄丒丒丒偺傛偆偵悢偊偰傕偱偒傑偡偑
俀恑朄昞婰偵偡傟偽丄傕偭偲娙扨偵傢偐傝傑偡丅
係俋傪俀恑朄昞婰偵偡傞偲丄侾侾侽侽侽侾丂偲側傝傑偡偑丄侾偲侾偺娫偵偁傞侽偺悢+侾
偑摎偊偱偡偹丅乮扐偟丄侾偑侾偮偟偐側偄応崌偼侽僠乕儉偲峫偊傑偡丅乯
恄撧愳導戝夛偱偼
帋崌悢偼丄侾俋俈帋崌
侾夞愴偐傜嶲壛偡傞偲丄俉帋崌愴偆偙偲偵側傝傑偡丅
傑偨丄侾夞愴挷惍曽幃偺晄愴彑僠乕儉悢偼丄俆俉僠乕儉丄搑拞挷惍曽幃偺晄愴彑
僠乕儉悢偼丄係僠乕儉偱偡偹丅

乮儁儞僱亅儉丗Toru乯
乮侾乯 椺偵傛偭偰丄堷偒暘偗偼側偄傕偺偲偡傞偲丄堦帋崌偛偲偵晧偗偨堦偮偺僠乕
儉偑懳墳偟丄桪彑峑偩偗偑晧偗側偄偺偱
丂丂丂係俋乗侾亖係俉
係俉帋崌偲側傝傑偡丅
乮俀乯乮俁乯偺曽幃偲偡傞偲俀俆亖俁俀丄俀俇亖俇係偱偡偐傜
丂丂丂係俋仺俁俀仺侾俇仺俉仺係仺俀仺侾
偲寁俇夞彑偮昁梫偑偁傞偙偲偵側傝傑偡丅
乮俁乯 堦夞愴偺彑幰偲柶彍幰傪偁傢偣偰俁俀偲側傞傛偆偵偡傞傢偗偱偡偐傜柶彍偝
傟傞僠乕儉悢傪X偲偟偰
丂丂丂X亄乮係俋乗X乯乛俀亖俁俀
傪夝偄偰丄X亖侾俆丄偁傞偄偼尪偺僠乕儉俇係乗係俋亖侾俆僠乕儉傪壛偊偰俇係僠乕儉偲峫偊偰丄傒傫側堦夞愴傪傗傞偲峫偊傟偽丄尪僠乕儉偲懳愴偡傞僠乕儉偑晄愴彑偲側傝傑偡偐傜侾俆僠乕儉
乮係乯 係俋亖俀係x俀亄侾乮俀俆僠乕儉巆傞丄晄愴彑偼侾僠乕儉乯埲壓摨條偵
丂俀俆亖侾俀x俀亄侾丂侾俁亖俇x俀亄侾丂俈亖俁x俀亄侾丂係亖俀x俀丂俀亖侾x俀
偲偄偆偙偲偐傜晄愴彑偺僠乕儉偼偺傋係僠乕儉偲偄偆偙偲偵側傝傑偡丅傑偨乮俁乯偲摨條偵
婏悢偵側偭偨傜昁偢晧偗傞尪偺僠乕儉傪侾僠乕儉偨偡偲峫偊偨曽偑傛偄偐傕偟傟傑偣
傫丅
乮俆乯 恄撧愳導戝夛偺応崌傕摨條偵
丂乮侾乯侾俋俈帋崌乮俀乯俉夞乮俁乯俆俉僠乕儉乮係乯係僠乕儉
乮俇乯 搑拞挷惍曽幃偼埲慜帡偨栤戣偑偁偭偨傛偆側婥偑偟傑偡偑丄寢嬊侾傪壛偊傞
偐丄俀偱妱傞偲偄偆偙偲偵側偭偰丄俀恑朄偱彂偔偲尒捠偟偑傛偔側傞傛偆偱偡丅椺偊
偽係俋傪擇恑朄偱偼
丂丂丂係俋=110001=100000-1111
偐傜尪偺僠乕儉偑係僠乕儉昁梫丅
丂丂丂侾俋俉=11000110=100000000-111010
偱傗偼傝係僠乕儉丅

乮儁儞僱亅儉丗彫妛柤扵掋乯
乮侾乯侾帋崌枅偵侾僠乕儉徚偊偰偄偔偺偱丄係俋亅侾亖係俉帋崌偱偡丅
乮俀乯俀俇亜係俋亜俀俆偐傜俇帋崌偱偡丅
乮俁乯俀俇-係俋亖侾俆僠乕儉偱偡丅
乮係乯係俋亖俀係*俀+侾丆俀俆亖侾俀*俀+侾丆侾俁亖俇*俀+侾丆俈亖俁*俀+侾丆
係亖俀*俀丆俀亖侾*俀偐傜+侾偺悢偱偁傞係僠乕儉偱偡丅
栤偄乮係乯偵偮偄偰丄
栤偄乮俁乯偐傜俀俇-係俋亖侾俆偲側傝丄偙偺侾俆傪俀恑悢偱昞傢偡偲丄
侾侾侾侾偲側傝傑偡丅偙偺侾偺悢偼係偱偁傝丄係僠乕儉偑晄愴彑僠乕儉偺
崌寁偱偡丅
戞侾儔僂儞僪偱侾僠乕儉偑晄愴彑偲側傝丄
戞俀儔僂儞僪偱傕侾僠乕儉偑晄愴彑偵側傝傑偡偑丄偙偺僠乕儉偼俀僠乕儉偺彑偪忋偑傝僠乕儉側偺偱
俀僠乕儉傪晄愴彑偺婡夛偑梌偊傜傟偨僠乕儉亖晄愴彑岓曗僠乕儉偲屇傇偲偦偺悢偼俀偱偡丅摨條偵偟偰丄
戞俁儔僂儞僪丄戞係儔僂儞僪偺晄愴彑僠乕儉悢偼偦傟偧傟係丄俉僠乕儉偲側傝傑偡丅
偮傑傝丄僩乕僫儊儞僩昞偵彂偄偨応崌丄侾+俀+係+俉僠乕儉偼丄俆夞彑偰偽桪彑偱偒傑偡丅
偦偺堄枴偱侾夞愴挷惍曽幃偺晄愴彑僠乕儉偺悢侾俆偲摨偠偱偡丅

乮儁儞僱亅儉丗崅嫶丂摴峀乯
(1)侾帋崌偛偲偵侾僠乕儉偑攕戅偡傞偺偱丂48峑偑嫀傞偵偼48帋崌昁梫
恄撧愳戝夛偼丂197帋崌偱偡偹丅
(2)49傛傝戝偒偄嵟彫偺2n偺傗偖傜傪慻傓傢偗偱偡偐傜丂32<49<64傛傝
壦嬻偺僠乕儉64-49=15僠乕儉傪壛偊乮壦嬻偺僠乕儉偼偐側傜偢晧偗傞偲
憐掕偡傞偺偱偡乯丂15僠乕儉偑2夞愴偐傜49-15=34僠乕儉偑侾夞愴偐傜
愴偆帠偵側傝傑偡丅64=26傛傝丂6帋崌偟傑偡丅
恄撧愳戝夛偼丂128亙198亙256側偺偱丂256=28偐傜丂8帋崌偱偡
(3)丂(2)偱彂偄偨傛偆偵壦嬻偺僠乕儉偲愴偆偲憐掕偟偨15僠乕儉偑晄愴彑偲側傝傑偡
恄撧愳戝夛偺応崌偼256-198=58傛傝58僠乕儉偑晄愴彑偱偡丅
(4)
婏悢偺帪偼丂壦嬻偺侾僠乕儉傪楢傟偰偒偰懳愴丄嬼悢偺偲偒偼偦偺傑傑
2僠乕儉偯偮懳愴偡傞偲偄偆晽偵峫偊傞偺偱偡偐傜
婏悢偺偲偒偼侾傪懌偟偰俀偱妱傝丄嬼悢偺偲偒偼俀偱妱傞偙偲傪孞傝曉偟傑偡丅
丂49仺25仺13仺7仺4仺2仺1丂偲側傝
侾傛傝戝偒偄婏悢偺屄悢偼4偮側偺偱係帋崌偑晄愴彑偲側傝傑偡丅
暿夝
49(10恑朄)=110001(2恑朄乯傪1000...0乮俀恑朄乯偵偡傞偵偼丂
110001+1111=1000000側偺偱4帋崌偲側傝傑偡丅
偙偺曽朄偵偮偄偰愢柧偟傑偡丅
亙亙1111偺媮傔曽偵偮偄偰亜亜
偡傋偰偺寘偑1偵惉傞偵偼壗傪懌偡偲偄偄偐峫偊傑偡丅
1110傪懌偡偙偲偲偄偄偺偱偡偐傜乮0偺晹暘傪侾偵丂侾偺晹暘傪0偵偡傞乯
亄侾偟偰1111傪摼傑偡丅
亙亙偙傟偱弌傞棟桼亜亜
侾寘栚偑侾夞愴傪昞偟丂偙偙偱偼婏悢側偺偱侾僠乕儉傪楢傟偰偒
傑偡丅偡傞偲偼偠傔偺僠乕儉悢偼110010僠乕儉偱偁傞偲偒傪峫偊傞偲
偄偆帠偵側傝傑偡丅
崱搙偼俀寘栚偑2夞愴栚偱偙偺偲偒婏悢僠乕儉偵側傝傑偡偐傜侾僠乕儉
楢傟偰偔傞偙偲偵側傝僠乕儉悢偼110100傪偐傫偑偊傞偙偲偲摨偠丅
...偲摨條偵峫偊偰偄偔偲丄偳偺寘偐偑侾偲側傞偲偒丄偦偺寘偵侾傪懌偡
乮侾僠乕儉楢傟偰偔傞=晄愴彑乯偲偄偆偙偲偵側傞偙偲偑傢偐傝傑偡丅
偦傟偱1000...000偺宍偵側傞偲偄偄偙偲偑傢偐傝傑偡丅偙偺曽朄偱偼
1111偼丂侾夞愴2夞愴3夞愴4夞愴偱壦嬻偺僠乕儉偑昁梫乮晄愴彑乯偲偄偆
偙偲傕傢偐傝傑偡丅
198峑偺偲偒偼
夝侾
198仺99仺50仺25仺13仺7仺4仺2仺1丂傛傝侾傛傝戝偒側婏悢偼4偮側偺偱4帋崌
夝俀
198(10恑朄乯=11000110乮俀恑朄乯丂11000110+111010=10000000傛傝丂係帋崌偲
側傝傑偡丅
忋偲摨條偵丄偙偺111010偺娙扨側弌偟曽偼丂11000110+111001=11111111偲偄偆
傛偆偵偡傋偰侾偲惉傞傕偺傪尒偮偗丂111001+1=111010偵傛偭偰悢傪摼傞偙偲偱
弌偣傑偡丅
夝俁
忋偺夝侾偲夝俀偺曽朄傪棟夝偡傞偲丂師偺傛偆偵弌偡帠偑偱偒傞偙偲偑
傢偐傝傑偡丅
128亙198亙256傛傝丂256-198=58丂58(10恑朄乯=111010(2恑朄乯傛傝丂
4僠乕儉偑晄愴彑偱偦傟偼丂2,4,5,6夞愴栚偱偁傞丅

| teki | 岼偺柌 | Toru |
| 忨偺偍偠偝傫 | 傗側偣 | aa |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 宩偍偲偙 | 奰杮丂峗 |
| 崅嫶丂摴峀 | 彫妛柤扵掋 | 儕僫儔僀 |
| Y.M |

崱擭偺壞偺慡崙崅峑栰媴戝夛偼丄堬忛導戙昞偺忢憤妛墍偺桪彑偱廔傢傝傑偟偨丅 場傒偵忢憤妛墍偺帋崌悢偼俇帋崌偱偟偨丅 恄撧愳導戙昞偺墶昹彜戝偼巆擮側偑傜侾夞愴偱晧偗偰偟傑偄傑偟偨丅巆擮両丂
崱夞偺栤戣偼丄僉乕儚乕僪丄偄傗僉乕僫儞僶乕偑乽俀乿偱偁傞偙偲偵偍婥偯偒偱偟傚偆偐丠
乮係乯偵偮偄偰偼丄僠乕儉悢偲摍偟偄偐傕偟偔偼挻偊傞俀偺椵忔乮俀値乯偺拞偱嵟傕彫偝偄悢偐傜僠乕儉悢傪傂偄偨悢丄偙偺栤戣偺応崌偼丄
丂丂丂俇係亅係俋亖侾俆
偱偡偐傜侾俆偵側傝傑偡丅偙傟傪俀恑悢偵偟偨帪偵暲傇侾偺屄悢偑摎偊偵側傝傑偡丅
侾俆偲偄偆偺偼丄Toru偝傫偺夝摎偵偁傞傛偆偵尪偺僠乕儉悢偱偁傝丄偙偺尪偺僠乕儉偲懳愴偡傞僠乕儉偑晄愴彑偲傪峫偊傞偲傢偐傝傗偡偄偲巚偄傑偡丅彫妛柤扵掋偝傫偺夝摎傕摨條偱偡偹丅 崅嫶丂摴峀偝傫偺夝摎偺拞偱傕愢柧偟偰偄偨偩偄偰偄傑偡偺偱丄嶲峫偵側傞偲巚偄傑偡丅
僩乕僫儊儞僩愴偺慻傒曽偲俀恑朄偑偮側偑傞偲偄偆偺傕丄偍傕偟傠偄偱偡偹両

 E-mail
E-mail
 栠傞
栠傞
 top
top