Weekend Mathematics/問題/問題79
79.サイコロの問題
(1)サイコロを1回または2回ふり、最後に出た目の数を得点とするゲームを考える。 1回ふって出た目を見た上で、2回目をふるか否かを決めるのであるが、 どのように決めるのが有利であるか。
(2)上と同様のゲームで、3回ふることも許されるとしたら、2回目、3回目をふるか否かの決定は、 どのようにするのが有利か。
入試数学 伝説の良問100
安田亨
講談社ブルーバックス
(京大 1977)
(ペンネ−ム:リナライ)
解答1:サイコロ1回振った時の得点の期待値を求めると
1/6+2/6+3/6+4/6+5/6+6/6=21/6=7/2=3.5
となります
なので、期待値以上、つまり4以上出たら、そこでストップするのが賢いやり方だと思います

(ペンネ−ム:kiyo)
(1) 4以上ならやめる。
(2) 2回目の判断 5以上ならやめる。
3回目の判断 4以上ならやめる。

(ペンネ−ム:teki)
答え
(1) 1回目の目が3以下なら2回目を振り、4以上なら2回目を振らない。
(2) 1回目の目が4以下なら2回を振り、2回目で4以上が出れば3回目は振らない。
<理由>
(1)は比較的簡単です。
1回目で4以上が出た場合、それより大きい目(5、6)の出る確率は、1/3
一方、それより小さい目(1、2、3)の出る確率は、1/2となり、小さい目が出る確率の
方が大きくなるからです。
(2)は、ちょっと複雑です。
1回目に4が出た場合、次の2回の内、1回でも4以上が出る確率は、1-3/6*3/6=3/4
ですので、この場合は次を振る方がより大きな目になる確率の方が大きくなります。
次に2回目ですが、これは、(1)と同様の考え方をすれば、2回目で3以下であれば、
3回目を振る方が、確率は上がります。

(ペンネ−ム:杖のおじさん)
(1)2回目を振るかの判断は1回目の出た目の数が期待値より大きい時にはやめる、期待値未満の時は2回目を振ることになります。
1回目に出る確率は次の通りとなります。
期待値は、
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| 期待値 | 1/6 | 2/6 | 3/6 | 4/6 | 5/6 | 6/6 |
| 合計期待値 | 3.5 | |||||
期待値=1×(1/6)+2×(1/6)+3×(1/6)+4×(1/6)+5×(1/6)+6×(1/6)=3.5
従って、1回目4,5,6のときは期待値より大きいのでやめる。
1,2,3のときは期待値より小さいのでもう1回振る。
そして1または2がでたら残念でしたということになります。
(2)3回目まで振ることができる場合、3回目に出る目の確率は、
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 | 1/12 | 1/12 | 1/12 | 1/4 | 1/4 | 1/4 |
| 期待値 | 1/12 | 2/12 | 3/12 | 4/4 | 5/4 | 6/4 |
| 合計期待値 | 4.25 | |||||
期待値=1×(1/12)+2×(1/12)+3×(1/12)+4×(1/4)+5×(1/4)+6×(1/4)=4.25
従って1回目5,6のときは期待値より大きいのでやめる。
1,2,3,4のときは期待値より小さいので2回目を振ります。
2回目に4,5,6のときはそこでやめる。
1,2,3のときは3回目を振ります。
1または2が出たら、残念でしたということになります。
因みに、3回目に出る目の確率は次のとおりです。
1〜3までは、 (1/6)×(1/6)×3=1/12
4〜6までは、 (1/2)×(1/6)×3=1/4 となります。

(ペンネ−ム:夜ふかしのつらいおじさん)
サイコロの目はどれも同じように出るとします。
サイコロをふってkの目が出たとします。(kは1から6の整数)このあとn回サイコロをふって1回でもkよりも大きな目が出る確率pを考えます。これはn回続けてk以下の目が出る事象の余事象ですから、p=1−(k/6)n です。pの値を計算すると次の表のようになります。この表より4回以上サイコロをふれば1回は6の目が出ることが1/2以上の確率で起こることが分かります。
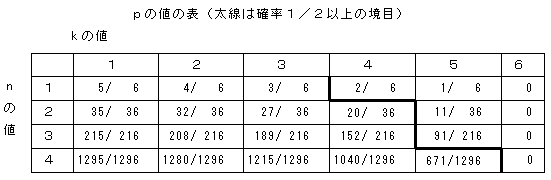
さて、何回でもサイコロをふってもよいのならば、当然6が出るまでふります。
あと1回だけしかふれないならば今サイコロの目が{1,2,3}ならばもう1回ふり、{4,5,6}ならふらないのがよいと思います。出る目の平均は、
(1+2+3+4+5+6)/6 = 3.5
だから、それより目が小さければ、もう1回ふると得することを期待できるからです。
難しいのはあと2回ふることを許されるときです。
今サイコロの目が{4}のとき、あと2回ふればそれより大きな目{5,6}が少なくとも1回出る確率は、20/36=5/9=0.5555・・・・ です。もしあと2回のうち1回目に{(5),6}が出ればよいのですが、そうでなかったとき、もう1回を一連の試行(あと2回ふること)の後半として思い切ってふるのか、あと1回だけふるとき出る目の平均値が3.5なので4より小さいと考えて自粛するのでしょうか。このあたりをどうするかはそのときの運とか流れによるのではないでしょうか。
解答
(1)1回目に{1,2,3}が出ればもう1回ふり、{4,5,6}が出れば止める。
(2)1回目に{1,2,3,4}が出ればもう1回ふる。
(「あと2回ふると{5,6}の出る確率が1/2より大きい」ことに期待して)
2回目は{1,2,3}が出ればもう1回ふる。(あと1回サイコロをふったときの平均値は3.5なので4以上が出ればふらない。1回目に「あと2回ふると・・・」と期待したことを修正する)
大勝ちを狙うより、負けないことでよしとする程度にしておく方が多くの勝負をするときには良いというのが実感です。

(ペンネ−ム:yokodon)
期待値で考えればいいですね。
ゲームの得点を確率変数と見て、これを X とし、X = k となる確率を P(k) とし
ます。
(1)この場合は、1回目までの得点 X の期待値 E(X) をさいころの出た目と比較す
れば良いですね。
P(k) = 1/6 (k = 1, 2, ..., 6) ですから、E(X) = 7/2
よって、さいころの目が 1〜3 の時には2回目に進み、4〜6 の時にはそこでやめ
るのが最適ということになります。
(2)2回目に関しては、問(1)で考えたので、3回目のみ考察します。
問(1)から、1回目の数字が 1, 2, 3 の時には必ず2回目に進むと考えて、
P(k) = (3/6)・(1/6) = 1/12 (k = 1, 2, 3)
他方、X = 4, 5, 6 となるのは、1回目が 4〜6 の時と、1回目が 1〜3 で2回目
が 4〜6 のときの2つの場合があるので、その和事象を考え
P(k) = 1/6 + (3/6)・(1/6) = 1/4 (k = 4, 5, 6)
となります。これを用いて得点の期待値を計算すると、E(X) = 17/4 で
これより、2回目のさいころの目が 1〜4 の時には3回目に進み、5 又は 6 の時
にはそこでやめるのが最適と言うことになります。

(ペンネ−ム:巷の夢)
(1)サイコロを一回振った場合の得点期待値は(1+2+3+4+5+6)/6=3.5となる。
因って一回目が3以下なら二回目を振り、一回目が4以上なら二回目は振らない。
(2)上記の行動を行ったとすると、サイコロを振った二回目までの得点期待値は以下のような考え方から4.25となる。
| 一回目 | 二回目 | 得点 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | |
| 3 | 3 | |
| 4 | 4 | |
| 5 | 5 | |
| 6 | 6 | |
| 2 | 1 | 1 |
| 2 | 2 | |
| 3 | 3 | |
| 4 | 4 | |
| 5 | 5 | |
| 6 | 6 | |
| 3 | 1 | 1 |
| 2 | 2 | |
| 3 | 3 | |
| 4 | 4 | |
| 5 | 5 | |
| 6 | 6 | |
| 4 | 4 | |
| 5 | 5 | |
| 6 | 6 |
例えば得点1の期待値は(1/6)×(1/6)×3=1/12となる。得点2,3も全く同様である。
得点4については(1/6)+(1/6)×(1/6)×3=3/12=1/4となる。得点5,6も全く同様である。
因って得点の期待値は (1+2+3)/12 +(4+5+6)/4=17/4=4.25
以上より、一回目が5以上なら二回目は振らない。一回目が4以下なら二回目を振り、二回目が3以下なら三回目を振る。二回目が4以上なら三回目を振らない。

(ペンネ−ム:SOU)
(1)
1〜6の目でだと、期待値は3.5なので、一回目が1〜3のとき
は振るべき。4〜6の時は振らないべき。
(2)
(1)と同様、1〜3だったら振るべき。ただ、一回触れる回数
が増えているので、4〜6で振るべきポイントがないかどうか、
考える。
イ)まとめると・・・
1回目に4の時、その後5または6になる確率を考える。
2回目で5または6が出る確率は
1/3
2回目で4以下が出て、3回目で5または6が出る確率は
2/3*1/3 = 2/9
以上のことから、
1/3+2/9 = 5/9
となり、一回目が4の時は振るべき。
ロ)
1回目が5の時は、同様に考えると1/2を下回るので振るべきでない。
ハ)
2回目の振り方については、(1)と同様。

(ペンネ−ム:Y.M)
(1)
1回サイコロを振ったときの出た目の期待値は、
(1/6)*(1+2+3+4+5+6)=3.5 ですから、
一回目の目の値が1,2,3であった→もう一度振り直す
一回目の目の値が4,5,6であった→そのままでやめておく
(2)
2回目の目が1,2,3であったら3回目投げる
2回目の目が4,5,6であったら投げない
とする。

(ペンネ−ム:高橋 道広)
(1) 期待値を求めます。
(1+2+3+4+5+6)/6=7/2であるから 平均して3.5が出るので 1〜3までのときは
もう一度振って 4,5,6のときは 振らない。
(2)
2回振った後での得点の期待値は1回振ったあとと状況が同じだから
その結果が1〜3までのときはもう一度振って 4,5,6のときは 振らない。
1回振った後でどうするかが 大問題です。
しかし 2回振った後の期待値を求めて比較するとよいのです。
もし2回目のさいころを振ったときに1〜3まででたら 得点の期待値は3.5
4,5,6のときは3回目を振らないので 得点は4,5,6
よって2回振ったときの得点の期待値は (3.5×3+4+5+6)/6=4.25
よって1回目に1〜4までなら2回目を振る 5,6なら振らない
2回目を振ったときに1〜3なら3回目を振る 4〜6ならふらない。
うまく説明できていませんね。日本語は難しい…。
2回振った時の期待値を求めるのがみそですね(^.^)
出た目が1〜5までなら もう一回振ったほうが有利になるのはこの試行を何回
以上くりかえすときなんでしょうか。

(ペンネ−ム:kirkland)
| A君 | 「直感ですが、(1)は、1回目が4以上だったらそこでストップ。(2)は、1回目が5以上だったらストップ、 2回目が4以上だったらストップですね。」 |
| 先生 | 「正解だが、その根拠は?」 |
| A君 | 「だって、そもそも2分の1の割合で4以上の目が出ますよね。1〜3か4〜6の2通りなんだから。 (1)は2回振るんだったら、2回のうち1回ぐらいは4〜6の目が出そうじゃないですか。だから、1回目で3以下の場合は再チャレンジです。理屈の上では、2回目には4〜6の目が出るはずです。」 |
| 先生 | 「ほうほう」 |
| A君 | 「同じ理屈で、5以上の目は3分の1の割合で出るはずです。1〜2、3〜4、5〜6の3通りですから。3回に1回 の割合で5以上の目が出ますよね。だから、(2)で1回目は4以下は強気で再チャレンジです。理屈の上では残り の2回のち1回は5以上の目が出るはずですから。しかし、ちょっと小心者の僕は、ビビって2回目は4しか出なく ても妥協してしまうわけです。」 |
| 先生 | 「強気とか弱気とかはあまり関係ないだろ、数学の問題なんだから。(2)で2回目の判断は、あと2回まで振ること ができるということで(1)と同じじゃないか。」 |
| A君 | 「なるほど。こんな簡単な考え方でいいんですか?」 |
| 先生 | 「厳密にはちゃんと計算した方が、スッキリいくんだろうが。ところでカーニバルの問題は覚えてるかい?」 |
| A君 | 「もちろん。小島先生に怒られちゃって、もうけ損ねました。う〜ん、残念!」 |
| 先生 | 「全然反省してないな!また怒られるよ!」 |
| A君 | 「理論上の平均値を考えるんですね。と、話をそらしつつ」 |
| 先生 | 「そうそう。1回サイコロを振ったら平均してどれくらいの目が出る?」 |
| A君 | 「理屈の上では、6回振ったら1〜6の目が1回ずつ出るんだから、平均して(1+2+3+4+5+6)÷6=3.5 ですね。というわけで、(1)だと、2回目に平均して3.5の目が出るはずから、1回目が平均以下だと再チャレン ジなのですね。」 |
| 先生 | 「そのとおり。さて、(1)の戦略でいくと、平均してどれくらいの目が出るんだろう?」 |
| A君 | 「1回目でやめてしまう場合と、2回振る場合があって計算がややこしそうですね。」 |
| 先生 | 「まぁ、実験してみよう。」 |
| A君 | 「は〜い、振ってみま〜す!あっ、4ですね。もちろん、ここで終了ですね。」 |
| 先生 | 「本当に終了でいいのかなぁ〜、次に6が出るかもしれないよ〜。ファイナルアンサー?」 |
| A君 | 「ファイナルアンサーですよ!」 |
| 先生 | 「じゃあ仕方ないなぁ。4なんだね。最終結果は4にしておこう。ところで、2回目の目は気にならない?」 |
| A君 | 「う〜ん気になりますね。2回目も振ってみます。あっ、先に言っておきますけど、僕は4でストップしたので、2回 目に3以下が出ても4はキープですよ、絶対!試しに振ってみるだけなんですからね!」 |
| 先生 | 「OK、OK。まぁ、試しに振ってみなさい。」 |
| A君 | 「えいっと。ぎぇ〜〜!6が出た〜〜!」 |
| 先生 | 「なぁ、言った通りだろ!でも、君は4をキープしたので4だよ〜!ざまぁ〜!」 |
| A君 | 「こんな不幸な〜!とほほ……。んっ、分かりましたよ!1回目が4〜6だと勿論ストップなんですが、これをキープ しておいて2回目の目も確かめればいいんですよ!そうすれば、一喜一憂ありますが、いつも2回振ることになって 計算が楽そうです。う〜んと、表に整理すると下のようになります。」 |
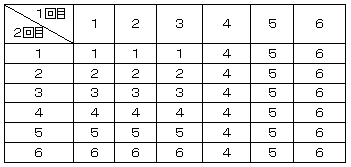
| 先生 | 「よくぞ気付いたね!」 |
| A君 | 「え〜と、合計36通りの目の出方があって、1になるのは3通り、2になるのも3通り……。平均すると、4.25です ね。」 |
| 先生 | 「その通り。これで、(2)もできただろ。」 |
| A君 | 「はい。3回まで振ることのできる場合、2回目と3回目の2回を(1)のような戦略でいくと平均して4.25の目を 出せるから、1回目は4以下だと再チャレンジなのですね。」 |
| 先生 | 「はい、じゃあ今月はここまで。さようなら〜」 |
| A君 | 「ところで、先生。4回まで振ってもいい場合とか、5回まで振っていい場合とかはどうなるんですかね?」 |
| 先生 | 「君もしつこいねぇ。計算が面倒なので、辞めだ辞めだ。誰かが計算してくれるよ、きっと。結論だけ言っておくと、 4回も5回もそんなに変わらないよ。6回まで振っていい場合で初めて、1回目が5以下で再チャレンジだ。 では、本当にさようなら〜〜。」 |

(ペンネ−ム:Toru)
数学の問題ですから、やはり期待値で考えるのでしょう。
1) さいころを1回ふった時、でる目の数の期待値A(1)とすると、
A(1)=(1+2+3+4+5+6)/6=7/2 よって、1回あるいは2回ふるという場合は1回目の目
の数が7/2より小さければ2回目へ行く、7/2より大きければ終わりという戦略が有利
と考えられる。すなわち、1回目1、2、3ならもう一度ふる。4、5、6なら終わ
りにする。
2) 1)のような戦略で1回あるいは2回さいころをふる時の得点の期待値をA(2)
とすると、A(2)=(4+5+6)/6+1/2xA(1)=51/12=4.25 つまり3回ふることを許される場
合は、1回目にこれより小さな目がでれば2回目以降へ進み、大きな数字が出ればそ
こで終わりとするのがよい。2回目から3回目へ行くかどうかは1)と同じ。すなわち、
1回目5、6なら終わり。1、2、3、4なら2回目をふり、2回目が4、5、6な
らそこで終わり。1、2、3ならさらに3回目をふる。
3) おまけ 2)の方法で1or2or3回ふった時の得点の期待値A(3)とすると
A(3)=(5+6)/6+2/3xA(2)=14/3<5同様にA(4)=(5+6)/6+2/3xA(3)=89/18<5,
A(5)=(5+6)/6+2/3 x A(4)=277/54>5
と5回ふるのを許されると初めて期待値が5を超えるから6回以上ふってよい場合は、6以外ではもう一度ふるのがよいと考えられる。6が最高点でこれ以上はない。

(ペンネ−ム:aa)
(1)サイコロを1回振って出る目の期待値は、(1+2+3+4+5+6)/6=3.5。
よって、1回目が1〜3のときは、2回目を振ったほうが期待値が上がる。
1回目が4〜6のときは、2回目を振らない。
このときの期待値は、(3.5+3.5+3.5+4+5+6)/6=4.25となる。
(2)(1)より、サイコロを2回振るときの期待値は、4.25であるから、
1回目が5,6のときは、2回目を振らない。
1回目が1〜4のときは、2回目を振る。3回目を振るか否かは、(1)と同じ。
このときの期待値は、(4.25+4.25+4.25+4.25+5+6)/6=4.666...
Excel使って期待値計算してみました。
| 振る回数 | 期待値 |
|---|---|
| 1回 | 3.500000000000000 |
| 2回 | 4.250000000000000 |
| 3回 | 4.666666666666670 |
| 4回 | 4.944444444444440 |
| 5回 | 5.129629629629630 |
| 6回 | 5.274691358024690 |
| 7回 | 5.395576131687240 |
| 8回 | 5.496313443072700 |
| 9回 | 5.580261202560590 |
| 10回 | 5.650217668800490 |
| 20回 | 5.943508200715050 |
| 30回 | 5.990876259027990 |
| 40回 | 5.998526464896180 |
| 50回 | 5.999762015854150 |
| 60回 | 5.999961564231800 |
| 70回 | 5.999993792408850 |
| 80回 | 5.999998997439370 |
| 90回 | 5.999999838080860 |
| 100回 | 5.999999973849160 |
| 110回 | 5.999999995776490 |
| 120回 | 5.999999999317880 |
| 130回 | 5.999999999889830 |
| 140回 | 5.999999999982210 |
| 150回 | 5.999999999997130 |
| 160回 | 5.999999999999540 |
| 170回 | 5.999999999999920 |
| 180回 | 5.999999999999990 |
| 184回 | 5.999999999999990 |
| 185回 | 6.000000000000000 |
185回目で計算精度から期待値が6.0になりました。
感覚的には、10回も振れば1回くらいは6が出そうですが、期待値としては、
5.65程度なんですね。

| kiyo | teki | aa |
| Toru | 巷の夢 | 杖のおじさん |
| 高橋 道広 | SOU | yokodon |
| Y.M | 夜ふかしのつらいおじさん | kirkland |
| リナライ |

今回の問題はちょっとむずかしかったでしょうか?
数学的には、期待値を計算して出た目の数とそれとを比較して次のとるべき行動を決定すればいいということになります。まあ、人生はこう計算通りにはいきませんけれどね・・・。
高橋 道広さんの問いかけに、Toruさん、aaさんが答えてくださいました。A君、わかったかな?
サイコロを最大6回まで振っていいとすると、 1回目に5がでても、それでやめないほうがいいということになります。 6回に1回くらいは6がでると考えるとまあ妥当な線でしょうね。

 E-mail
E-mail
 戻る
戻る
 top
top