Weekend Mathematics/問題/問題78
78.連続自然数の問題
いくつかの連続な自然数の和が1000であるとき、この連続な自然数を求めよ。
入試数学 伝説の良問100
安田亨
講談社ブルーバックス
(山形大・人文 1989)
(ペンネ-ム:やなせ)
お答えは5個と25個ですね
198~202と28~52なんですが
他に無いといった説明が未だできていない
途中経過です(笑)
3組目発見しました。55~70(16個)ですね。
1から順に足し込んでいくと45まで行くと1000越えちゃいますのと
連続した組み合わせの数字ってところから
使用する数字の数は2個~44個までの組み合わせになりますね
でもこっからさきの説明<釈明?がでけもうさん
最初の二組は1000を適当に割っていって考えつきました
1.2.3&3.4.5.6.7の場合で考えると
真ん中の数字に使用した数字の個数で倍数すると合計数になることからね
んで28~52で25個、198~202で5個になっちゃいました
先生がもう一組有ると教えてもらったので
5と25の間で14~16個ぐらいのはずと、やりましたところ
前出のお答えですがこれ又導けないし、証明ができません
まさか偶数使用とは考えもつきませんでした。

(ペンネ-ム:仮面X)
最初、332+333+334=999と考えたらわかりました。
1000にするには、真ん中を偶数にして、前後に2つずつ足して奇数個にする。
1000=200×5、1000=40×25、1000=8×125だから
198+199+200+201+202=1000
28+29+30+31+32+33+34+35+36+37+38+39+40+52+51+50+49+48+47+46+45+44+43+42+41=1000
そしてもう一つありました。偶数個でも作れました。
1000=8×125からも作れます。2つ足して奇数125になるのを、
偶数8組つくれればいいので
125=62+63=61+64=60+65=59+66=58+67=57+68
=56+69=55+70
だからまえの2つとあわせて、
こたえ 198から202と28から52と55から70

(ペンネ-ム:テモ)
なんとなくすぐに分かりました。
198, 199, 200, 201, 202 の5つの連続数。
出来た!
でも待てよ?これ以外にないものか考えました。
奇数で1000がちょうど割り切れるものならば良いのでは?
25の場合40の前後のそれぞれ12個 28~52
125の場合 8の前後のそれぞれ62個 -54~70 ←負だから×
答え:上記5個と25個の2つの場合
偶数の個数の場合がまだ有りました。
55から70までの16個!
答え:5個と16個と25個の3つの場合
因みにもっと大きな数字の場合も計算してみました。
10,000,000のとき
| 1,638 から | 3,125個 |
| 7,173 から | 1,280個 |
| 15,688 から | 625個 |
| 38,935 から | 256個 |
| 79,938 から | 125個 |
| 399,988 から | 25個 |
| 1,999,998 から | 5個 |

(ペンネ-ム:杖のおじさん)
◎エクセルを使用して調べました。
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 1 | -999 | #N/A |
| 2 | 3 | 2 | -997 | #N/A |
| 3 | 6 | 3 | -947 | #N/A |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 52 | 1378 | 52 | 378 | 28 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 70 | 2485 | 70 | 1485 | 55 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 202 | 20503 | 202 | 19503 | 198 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 250 | 31375 | 250 | 30375 | #N/A |
A1のセルに数式を入力
B1*(B1+1)/2
B1のセルに1を入力
B欄は1から始まる自然数を入力
C1のセルに数式を入力
A1-1000
D1のセルに数式を入力
vlookup(c1,$A$1:$B$250,2,0)+1
1行目入力したらドラッグして250行までコピーする。
答えは、D欄に出た数字からB欄の数字までの自然数になります。
従って、28から52、55から70、198から202の3つとなります。
答えは瞬時に出ます。
◎CASIO FX-870PとCASIO FX-890Pを使用してBASICで計算して調べました。
プログラムは次のとおりです。
10 DIM Z(250),Y(250) 20 CLS:INPUT"250マデノスウジ",E 30 FOR A=1 TO E 40 B=A*(A+1)/2 50 Z(A)=B:Y(A)=B-1000 60 NEXT A 70 FOR C=1 TO E 80 FOR D=1 TO E 90 IF Z(C)=Y(D) THEN PRINT C+1;"カラ";D;"マデ":BEEP:GOTO 110 100 NEXT D 110 NEXT C 120 BEEP1:BEEP0:BEEP1:BEEP0 130 IF INKEY$="" THEN 130 140 GOTO 20
実行すると、250マデノスウジ? と聞いてきますので、250を入力し、[EXE]を押すと、結果は、
28カラ52マデ
55カラ70マデ
198カラ202マデ
と表示されます。答えがでるたびBEEP音で知らせてくれますので、それまでコーヒーでも飲んで楽しみながら待っています。30分20秒かかりました。

(ペンネ-ム:kiyochan)
連続した自然数の個数をn、はじめの自然数をxとすると
nx+(n-1)n/2=1000
∴n(2x+n-1)=2000
ここで自然数であることにより、n=奇数 2x+n-1=奇数のとき
、奇数×奇数=奇数となり存在しません。
n=偶数 2x+n-1=偶数のとき、
ここで、
2x+n=偶数+1=奇数となり、
n=偶数のためxは自然数として存在しません
n=奇数 2x+n-1=偶数のとき、
n(2x+n-1)=2000が成立する自然数は、
n=5 2x+n-1=400----①
①より n=5 x=198
答え 198,199,200,201,202
198~202までの自然数
n=25 2x+n-1=80----②
②より n=25 x=28
答え 28,29,30,31,32,
33,34,35,36,37,
38,39,40,41,42,
43,44,45,46,47,
48,49,50,51,52
28~52までの自然数
n=偶数 2x+n-1=奇数のとき
n(2x+n-1)=2000が成立する自然数は、
n=16 2x+n-1=125----③
③より n=16 x=55
答え 55,56,57,58,59,60,61,62
63,64,65,66,67,68,69,70
55~70までの自然数

(ペンネ-ム:teki)
28~52、55~70、198~202 の3種類
<解法>
連続した自然数の最初の数をm、(連続する)個数をnとすると、総和は、
m*n+n*(n-1)/2 となります。
nで整理すると、
n*(2m+n-1)/2 =1000
∴ n*(2m+n-1)=2000
よって、n及び2m+n-1はいずれも2000の約数です。
また、nの最大値は、∑n≦1000 より、44となります。
44以下の2000の約数は、2、4、5、8、10、16、20、25、40の8つですが、
条件に合致(mが自然数となる)するのは、n=5、16、25 の3つのみです。
また、この時、m=198、55、28 となります。

(ペンネ-ム:kiyo)
初項をa、項数をnとしたたき終項はa+n-1。
ガウスの方法より、
n(2a+n-1)=2000=24*53 ..................(1)
2a+n-1>n ..................................................(2)
nが偶数のとき、2a+n-1は奇数でなければならない。(3)
nが奇数のとき、2a+n-1は偶数でなければならない。(4)
(2),(3),(4)より、
n=1,a=1000 (1000)
n=5,a=198 (198-202)
n=25,a=28 (28-52)
n=16,a=55 (55-70)
以上です。

(ペンネ-ム:夜ふかしのつらいおじさん)
連続する最初の自然数をnとし、連続する個数をkとします。すると、
| (n)+(n+1)+(n+2)+・・・+{n+(k-2)}+{n+(k-1)} | |
| = | kn+1/2・k(k-1) = 1000 ・・・・・・ (あ) |
2000 の約数の表
| 20=1 | 21=2 | 22=4 | 23=8 | 24=16 | |
|---|---|---|---|---|---|
| 50= 1 | 1 | 2 | 4 | 8 | 16 |
| 51= 5 | 5 | 10 | 20 | 40 | 80 |
| 52= 25 | 25 | 50 | 100 | 200 | 400 |
| 53=125 | 125 | 250 | 500 | 1000 | 2000 |
上の表より、kの候補を小さい順に調べます。
| k | 1 | 2 | 4 | 5 | 8 | 10 | 16 | 20 | 25 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2n+k-1 | 2000 | 1000 | 500 | 400 | 250 | 200 | 125 | 100 | 80 | 50 |
| 2n | 2000 | 999 | 497 | 396 | 243 | 191 | 110 | 81 | 56 | 11 |
| n | 1000 | × | × | 198 | × | × | 55 | × | 28 | × |
この結果より、4つの場合があります。

(ペンネ-ム:浜田 明巳)
最初の自然数をn,個数をkとすると,
k{n+(n+k-1)}/2=1000
∴k(2n+k-1)=2000=24×53
n,kは自然数なので,
kが偶数の時,2n+k-1は奇数,kが奇数の時,2n+k-1は偶数.
また,
(2n+k-1)-k=2n-1>0 (∵n≧1)
∴2n+k-1>k
∴(k,2n+k-1)=(1,2000),(5,400),(16,125),(25,80)
∴(n,k)=(1000,1),(198,5),(55,16),(28,25)
故に求める連続する自然数は,
28~52,55~70,198~202,1000

(ペンネ-ム:yokodon)
題意の自然数の個数を n 、その最初の数を a とします。
n 個の連続した自然数の和は、計算すれば分かるように an + 1/2・n(n - 1) です
から、題意の条件から
an + 1/2・n(n - 1) = 1000
・・・が成り立ちます。これを整理して、
n・(2a + n - 1) = 2000
を得ます。
さて、a 及び n を自然数としたので、
(2a + n - 1) - n = 2a - 1 ≧ 1(> 0)
・・・に注意して、満たす n と 2a + n -1 の値の組の候補は以下の 10 通りに限ら
れます。
(n, 2a + n - 1) = (1, 2000), (2, 1000), (4, 500), (5, 400), (8, 250), (10,
200), (16, 125), (20, 100), (25, 80), (40, 50)
このうち、n 及び a が共に整数になるのは、
(n, a) = (1, 1000), (5, 192), (16, 55), (25, 28)
・・・の4つです。
従って、求める連続な自然数は(1個の場合も連続とみなして)、
1個の場合:1000
5個の場合:192 ~ 196
16個の場合:55 ~ 70
25個の場合:28 ~ 52
・・・です。
#なお、
#(2a + n -1) - n = 2a - 1 ≡ -1 (mod 2)
#なので、2a + n -1 と n とで偶奇が異なることを利用すると、
#若干は簡潔な議論になる(候補が4つまで絞れる)でしょうが、
#本問では全部数え上げても大差無いかも。
ついでに、ここで「ある自然数が2個以上の連続する自然数の和となるための条件
は何か」という問いに自然に興味が湧きますが、これはどなたかがきっと続きの解説
をして下さると思うので、お任せします。

(ペンネ-ム:三角定規)
n+1 からn+k までの連続k個の自然数の和は
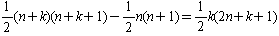
題意より
k(2n+k+1)=2000=2453 ………①
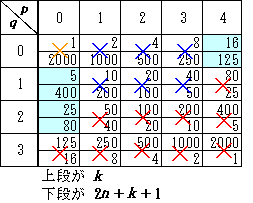 ①よりkは2p5q( 0≦p≦4,0≦q≦3)の形
で表すことができ,右表のとおりである。
①よりkは2p5q( 0≦p≦4,0≦q≦3)の形
で表すことができ,右表のとおりである。
ここで,k<2n+k+1 であること,さらに,
2n+1 が奇数だからkと2n+k+1 がともに偶数
になることはないことを考慮すると,①を満たす
(k,2n+k+1 )は,
(k,2n+k+1 )=(5,400 ),(16,125 ),(25,80 )の3組である。このとき,
(k,n )=(5,197),(16,54),(25,27)
∴(n+1,k)=(198,5),(55,16),(28,25)
[答](198,199,200,201,202) (5個)
(55,56,…,69,70) (16個)
(28,29,…,51,52) (25個)

(ペンネ-ム:午年のうりぼう)
m、nを1≦m≦44、0≦n≦999である整数とすると、題意は下のように表される。
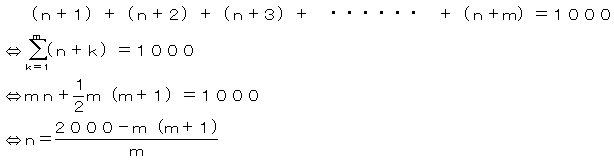
上式のmとnとの関係は下表のように表される。
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| n | 999 | 498.5 | 331.333 | 247.5 | 197 | 163.167 | 138.857 | 120.5 | 106.111 | 94.5 |
| m | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| n | 84.9091 | 76.8333 | 69.9231 | 63.9286 | 58.6667 | 54 | 49.8235 | 46.0556 | 42.6316 | 39.5 |
| m | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|
| n | 36.619 | 33.9545 | 31.4783 | 29.1667 | 27 | 24.9615 | 23.037 | 21.2143 | 19.4828 | 17.8333 |
| m | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|
| n | 16.2581 | 14.75 | 13.303 | 11.9118 | 10.5714 | 9.27778 | 8.02703 | 6.81579 | 5.64103 | 4.5 |
| m | 41 | 42 | 43 | 44 |
|---|---|---|---|---|
| n | 3.39024 | 2.30952 | 1.25581 | 0.22727 |
上表より、(m,n)=(1,999),(5,197),(16,54),(25,27)
従って、求める連続な自然数は、

(ペンネ-ム:小学名探偵)
答え (198から202) と (55から70) と (28から52)
一番目の数をa、最後はn番目とすると
n*(2*a+n-1)=2000=24*53 式(0)

(ペンネ-ム:モルモット大臣)
問題は連続する整数の和が1000になる組み合わせを求めよです。
そこで連続整数の先頭数字をB, 最後の数字をAとすると(A≠B)
1000=A(A+1)/2-(B-1)B/2よりこの式を変形して
2000=A2+A-B2+B=(A+B)(A-B)+A+B=(A+B)(A-B+1)
A+BとA-Bの偶奇性は同一であることからA+B,A-B+1の偶奇性は異なることに注目して
2000=(A+B)(A-B+1)=400×5, 125×16, 80 ×25の組み合わせがある。
(A+B)(A-B+1)=400×5よりA=202, B=198
(A+B)(A-B+1)=125×16より A=55, B=70
(A+B)(A-B+1)=80×25よりA=28,B=52
以上から求める答の組み合わせは次の3通り
(198,199,200,201,202) (55,56,57,・・・68,69,70) (28,29,30,・・・50,51,52)

(ペンネ-ム:Nと?)
1000が連続した自然数の和なので、
自然数の数をn
1番小さな自然数(数列の初項?)をa
1番大きな自然数(数列の末項?)をlとする。[l=a+n-1ということ]
すると、
1000=(a+l)*n/2 となる。
変形して、2000=(2a+n-1)*n
ここで、nが奇数ならば、2a+n-1は偶数となり、
nが偶数ならば、2a+n-1は奇数となので、
2000=奇数×偶数の形になる組み合わせを考える。
2000=24*53
なので、考えられる組み合わせは、
a. 2000=2000*1
b. 2000= 400*5
c. 2000= 80*25
d. 2000= 16*125
パターンa.からは
【n=1:1000を1つの連続した自然数の和で表す】
1000(1個だけでも連続と解釈する?)
【a+l=1:中央の・・・】
これはない。
パターンb.からは n=5
【1000を5つの連続した自然数の和で表す】
198+199+200+201+202
【a+l=5:中央の2つが2と3である200個の自然数】
これはない。
パターンc.からは
【n=25:1000を25個の連続した自然数の和で表す】
28+29+ +51+52
【a+l=25:中央の2つが12と13である40個の自然数】
これはない。
パターンd.からは、
【n=125:1000を125個の連続した自然数で表す】
これはない。
【a+l=125:中央の2つが62と63である16個の自然数】
55+56+ 69+70
以上より、組み合わせは4通りで、
1000(1個だけ)
198+199+200+201+202(5個)
28+29+ +51+52(25個)
55+56+ 69+70(16個)

(ペンネ-ム:Toru)
自然数の並びの初項をM、最終項をNとすると (M+N)(N-M+1)/2=1000 より
(M+N)(N-M+1)=2000=24x53
これから
M+N=2kx5l, N-M+1=24-kx53-l
(k=0,1,2,3,4、l=0,1,2,3)
とおくと、
2N+1=2kx5l+24-kx53-l,
2M-1=2kx5l-24-kx53-l,
第1式より、等式の右辺は奇数で、k=0 or 4、 k=0 の時 l=3とすると2M-1=109 よりM=55 N=70,l=2,1,0は2M-1<0となって不適。
k=4 の時l=3とすると同様にM=N=1000、l=2の
時M=198,N=202 l=1の時M=28,N=52、l=0 は2M-1<0で不適。
以上から
答え 28~52、55~70、198~202、1000の4通り

(ペンネ-ム:Chee)
いくつかの連続な自然数の和をnからn+kまでとして、
| n + (n+1) + ... + (n+k) | |
| = | 1 + 2 + ... + (n+k) - {1 + 2 + ... + (n-1)} |
| = | (n+k)(n+k+1)/2 - (n-1)n/2 |
| = | (k+1)(2n+k) / 2 |

(ペンネ-ム:巷の夢)
連続する自然数の最初をNとし、最後をN+nとすると、題意より
| 1000 | =N+(N+1)+(N+2)+・・・・・・+(N+n) |
| =(n+1)N+n(n+1)/2 | |
| =(n+1)(N+n/2) |
今回の問題は中々面白いですね。我々が一般的に経験することも大学の入試問題になると言う証明ですね。ひとつの数も連続する数と見なしました。

(ペンネ-ム:H.N)
答え
過程
S=A+A+1+A+2+・・・・・・+A+N=1000 とする。
このままNを自然数として計算するのは大変なので奇数と偶数の場合にわける
Ⅰ Nが奇数のとき
N=2K+1 とする
S=K(2A+2K-1)=1000 とあらわせる。
上の式を変形すると
2A=1000/K -(2K-1)
ここで左辺は偶数より右辺もまた偶数でなければならない
また1000=23×53より
右辺が偶数であるためには
K=23 OR 23×5 OR 23×52
OR 23×53
ここでAは自然数なのでA>0となるので
上のうちで K=23 のみこの条件をみたす
つまりK=8、A=55 →(1)の答え
Ⅱ Nが偶数のとき
N=2K とする
S=(2k+1)(A+K)=1000 とあらわせる。
上の式を変形すると
A=1000/(2K+1) -K
Aが自然数なのでK=2 OR 12 となる
よって K=2、A=198 →(2)
K=12、A=28 →(3)
となる

(ペンネ-ム:Y.M)


(ペンネ-ム:桂おとこ)
連続する最初の数を a 最後の数を a+b とおくと台形の面積を求める公式が使える。すなわち
(a+a+b)(b+1)÷2=1000から (2a+b)(b+1)=2000=24・53
(2a+b)と(b+1)の偶数・奇数は一致しないので
(2a+b)(b+1)=(2000,1)or (400,5)or(80,25)or(125,16) or(1,2000)or(5,400)or(25,80)or(16,125)
しかし(2a+b) >(b+1)から
(2a+b)(b+1)=(2000,1) or (400,5) or (80,25) or (125,16)となって
従って (a,b)=(1000,0) or (198,4) or (28,24) or (55,15)
よって求める答えは 198から 202 28から52 55から70 の3個です。
一般に 整数Nを連続した幾つかの自然数に分解する方法はNの奇数の約数の個数に等しいから
この場合3個で求める答えの個数に一致している。

(ペンネ-ム:高橋 道広)
自然数の最初の数をa 最後の数をa+bとします。(b+1個ある) 別解 Ⅱ数字の個数が偶数個のとき 後半の解答は他の方に以前教わった方法です。こうすると小学生でもとける問題
になるようです。大阪大学で文系の問題として1999年に出題されています。
このときの和は500でした。 (ペンネ-ム:aa) 次の(1)と(2)に場合分けします。 (1)偶数個の整数が連続している場合 (1)偶数個の整数が連続している場合の自然数の和は、 (2)奇数個の整数が連続している場合の自然数の和は、 以上より、求める自然数は、 (ペンネ-ム:ひろぽん) 連続する自然数が、偶数個並ぶ場合と奇数個並ぶ場合に分けて、考察する。 (ペンネ-ム:kirkland) 「いくつかの連続な自然数」と言ったときに、「1000」というのは解答になりうるのでしょうか?
日常の言葉の感覚でいうと、単独のものは解答にならないでしょうね。
でも数学の世界では、それも含めて考えたほうが自然(例外にするほうが不自然、というか処理が面倒くさい?)かもしれません。出題する段階で、それを明確にしておくべきでしたね、ご迷惑をおかけしました。
この場合、「1000」を含めても含めなくても、点数をつけることになると思います。
因みに、出典(ブルーバックス「入試数学伝説の良問」)の方では「1000」を解答とは扱っていません。 初項a、項数nというように、変数を設定して和を表している方が多かったわけですが、
この変数のおき方が大きく分けて3通りあっておもしろいなあと思いました。
それぞれ和は次のようになります。 このとき、遇奇性(パリティ)に注目すると、検証する回数をぐっと減らすことができます。 また、こういった問題の場合、条件に合うものをすべて挙げる必要があります。
ですから条件に合うものを挙げて終わりではなく、これ以外にはないということを示す必要があるわけです。
今回の場合、先入観からか、偶数個のケース(55~70の16個)を見落としてしまう方が何人かいらっしゃいました。 発展問題を出典(ブルーバックス「入試数学伝説の良問」)から引用します。
更にもう1つ、桂おとこさんの解答にある以下のことを示してください。
整数Nを連続した幾つかの自然数に分解する方法はNの奇数の約数の個数に等しい
和は (b+1) (a+a+b)/2=1000から (b+1)(2a+b)=2000=24×53
b+1と2a+bの偶奇は一致しないので一方は必ず奇数であることに気をつけると
(b+1,2a+b)=(1、2000),(5、400),(25,80)(125,16), (2000,1)
(400,5),(80,25)、(16,125)
1
198,199,200,201,202
28,29,30,...52
55,56,57,...70
Ⅰ 数字の個数が奇数個のとき
数字が並んでいるとき 平均がその真中の数になることから真中の数をx
個数をAとすると 500=AXとなる。
ここでAが奇数であるから A=5,25,125 x=200 40 8
A=5のとき (2つの数),200,(2つの数)と並んでいるので 最初の数は200-2=198
198,199,200,201,201
A=25のとき (12個の数),40,(12個の数)と並んでいるので 最初の数は40-12=28
28,29,30...52
A=125のとき (64個の数),8,(64個の数)と並んでいるので 最初の数は負になるから
題意をみたさない
数字が並んでいるとき 平均がその真中の2つの数の平均数になることから
真中の2つの数の和をx 個数をAとすると 500=AX/2となる。
ここでXが奇数であるから x=5,25,125 A=400 80 16
x=5のとき (198個の数),2,3,(98個の数)となるから最初の数は負となり
題意を満たさない
x=25のとき (39個の数),12,13,(39個の数)となり最初の数は負となり
題意を満たさない
x=125のとき (7個の数),62,63,(7個の数)となり最初の数は 62-7=55となる
このとき 55,56,57,58,...70となる。

解答・その23
(2)奇数個の整数が連続している場合
2個の時は、n、n+1なので、2n+1
4個の時は、n-1、n、n+1、n+2なので、4n+2
6個の時は、同様に6n+3
m個の時は、m(2n+1)である。(m=2,4,6...)
(このときの連続する整数は、n-m/2+1~n+m/2である)
よって題意は、m(2n+1)=1000となるm、nを求めることになる。(mは偶数,n>0)
一方、1000=23×53なので、1000の約数は2x×5yの形になる。
(2n+1)は奇数なので、候補としては、x=0、y=0,1,2,3として、1,5,25,125となる。
(a)2n+1=1の場合
これは、n=0となり、自然数でないので不当。
(b)2n+1=5の場合
n=2,m=200. -197~202の和が1000であるが、自然数以外を含むので不当。
(c)2n+1=25の場合
n=12,m=40. -27~52の和が1000であるが、自然数以外を含むので不当。
(d)2n+1=125の場合
n=62,m=8. 55~70の和が1000となる。
1個の時はn
3個のときは、n-1、n、n+1なので3n
5個の時は同様に5n
m個の時は、mnである。(m=1,3,5,...)
(このときの連続する整数は、n-(m-1)/2~n+(m-1)/2である)
よって題意は、m×n=1000となるm、nを求めることになる。(mは奇数,n>0)
(1)と同様に、mの候補は、1,5,25,125である。
(a)m=1の場合
n=1000。連続する自然数は1000のみ。
(b)m=5の場合
n=200。連続する自然数は、198~202.
(c)m=25の場合
n=20。連続する自然数は、8~32。
(d)m=125の場合
n=8.-54~70の和が1000になるが、自然数以外を含むので不当。
55~70
1000
198~202
8~32。
でも、1000(単独)を連続する自然数と言えるかは微妙ですねー。

解答・その24
以下に示すように、連続する自然数を前半・後半に分ける数字を、それぞれ、mとm+1とする。
・・・m-2,m-1,m|m+1,m+2,m+3…
このとき、mとm+1を始めとして、前半・後半の両側の数の和は、常に2m+1となる。
例:m+(m+1)=(m-1)+(m+2)=(m-2)+(m+3)=・・・=2m+1
この、組み合わせの個数をk個とすると、以下のような式を解けば良いことがわかる。
(式) (2m+1)*k=1000
1000=23*53に注意して、これを解くと、以下のようになる。
以下に示すように、連続する自然数の真中の数字をmとする。
・・・,m-2,m-1,m,m+1,m+2,…
このとき、mを中心に、両側の数の和は、常に2mとなる。
例:(m-1)+(m+1)=(m-2)+(m+2)=(m-3)+(m+3)=・・・=2m
この、組み合わせの個数をk個とすると、以下のような式を解けば 良いことがわかる。
(式) m+2k*m=1000 ⇔ (2k+1)m=1000
これは、『1.偶数個の場合』の式において、mとkを入れ替えた式であるため、同様に解けば良い。
以上から、解は以下の3通り
5個連続:198,199,200,201,202
16個連続:55,56,...,62,....,70
25個連続:28,29,…,40,…,51,52 以上

解答・その25
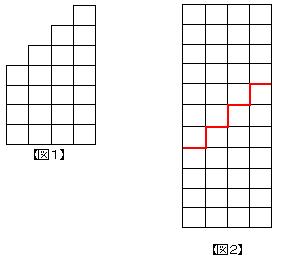
A君 「今月は、先生が出張中なので、僕一人で解きま~す!ところで、自然数とは何?辞書によると正の整数とありますね。正???小学生の僕にはよく分かりませんが、まぁ、1,2,3,……のことなんでしょうね。さて、連続する自然数の和っていうのは、たとえば、4+5+6+7みたいなもんだと考えると……。図示してみましょう。【図1】みたいな階段状の図で、正方形の個数の和と考えれますね。はははっ、全然正方形に見えませんな!タネも仕掛けもないこの階段を意味もなく2つ用意して、ひっくり返してくっつけると、あ~ら不思議、長方形になってしまいました【図2】。何が不思議やねん!!と、今日はつっこんでくれる相方もいないので、一人ボケつっこみをかましておいて…。
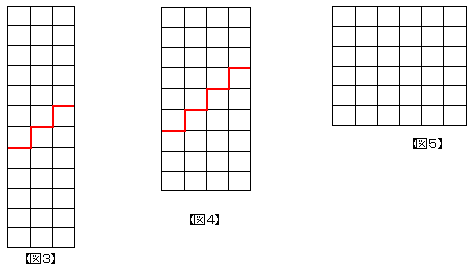
A君 さて、例によって小さい数で実験しますね。18ぐらいでいってみましょう。正方形18個でできる階段を2つくっつけると正方形の個数が36個の長方形ができますね。ということは、1×36、2×18、3×12、4×9、6×6のどれかですね。
縦の方が長いよな。1×36は軽く無視して、3×12【図3】。うまく、2つの階段に分けると。5+6+7で18になりますね。次は、4×9【図4】。これは、3+4+5+6で18ですね。6×6は……【図5】。げげっ!2つの階段に分けれぬ!偶数×偶数はダメなのかな?困りましたね~。先生の携帯にTELしてみましょう。
―――トゥルルルル――― あっ先生、教えて下さい。」
先生 「そもそも、こんな問題は方程式でやれば一発で解けるだろ!いま忙しいから、またあとで。ブツッ」
A君 「方程式なんて解けないこと知ってるくせに!!ブツブツ。図の対称性から考えていけば、いけそうなんだけど図を描くのが面倒なので、式で考えるとしますか。あんまりダラダラ長いと、誰も読んでくれなさそうだし……。
まず36=3×12=2×(3×6)=2×(6+6+6)=2×(5+6+7)ですな。中央の6は固定して、前の6を1減らす代わりに後ろの6を1増やせば階段が2つできるぞと。奇数個の数を足す場合はこんな感じでOK。
次は、36=4×9=2×(4×4.5)=2×(4.5+4.5+4.5+4.5)=2×(3+4+5+6)で見事に階段2つ。偶数個の数を足す場合は、真ん中の数が無いけれど、それぞれ0.5引く代わりに0.5足して、1.5引く代わりに1.5を足すとOK。
さて、36=6×6=2×(6×3)=2×(3+3+3+3+3+3)は、中央の数がない上、0.5ずつの調整もできないので、偶数×偶数はダメダメですな。というわけで、18の場合は、18=5+6+7と18=3+4+5+6の2通りです
―――トゥルルルル―――先生、これであってますか?」
「この電話は、現在電源が入っていないか、電波の届かない……。」
A君 「あっ、電源切ったな!畜生!こうなったら、自力で解いてやる。さて、1000ですな。階段2つで2000。
1×2000、2×1000、4×500、5×400、8×250、10×200、16×125、20×100、25×80、40×50で偶数×偶数はダメだし、1×2000は軽く無視して、5×400、16×125、25×80の3通りを考えればいいのよ。以下、ちょっと雑なのが気になりますが。
2000 =5×400
=2×(5×200)
=2×(200+200+200+200+200)
=2×(198+199+200+201+202)
というわけで、1000=198+199+200+201+202
2000 =16×25
=2×(16×12.5)
=2×(12.5+12.5+12.5+……+12.5+12.5+12.5)
=2×(5+6+7+……+18+19+20)
というわけで、1000=5+6+7+……+18+19+20
2000 =25×80
=2×(25×40)
=2×(40+40+40+……+40+40+40)
=2×(28+29+30+……+50+51+52)
というわけで、1000=28+29+30+……+50+51+52
―――トゥルルルル―――先生、これであってますか?」
先生 「素晴らしい!!いま私は上機嫌だ!!今日も勝ったぞ! ♪六甲おろしに~♪」
A君 「……出張って、ひょっとして甲子園?」

正解者
teki
テモ
夜ふかしのつらいおじさん
三角定規
kiyo
巷の夢
小学名探偵
Toru
やなせ
kiyochan
浜田 明巳
杖のおじさん
Nと?
Y.M
桂おとこ
ひろぽん
高橋 道広
H.N
仮面X
モルモット大臣
yokodon
Chee
aa
午年のうりぼう
kirkland

まとめ
私自身は1のパターンしか思いがいたらず、
案外3のパターンの式がシンプルだったりするので感心しました。
さらに、=2000として、それぞれの変数が自然数であるという条件の元に解を探していくことになります。
<発展問題>
m+(m+1)+・・・+(m+n)=Nとなる自然数m,nが存在するために自然数Nが満たす必要十分条件を求めよ。

 E-mail
E-mail
 戻る
戻る
 top
top