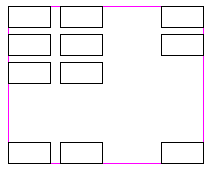
偨偰丄傛偙偺挿偝偑偦傟偧傟丂9cm丄13cm偺挿曽宍偺僞僀儖傪丄壓偺恾偺傛偆偵丂1cm偁偗偰丄
惓曽宍偵暲傋傑偟偨丅暲傋偨僞僀儖偼丄傕偭偲傕彮側偔偟偨偲偒壗枃偱偡偐丅
Weekend Mathematics乛栤戣乛栤戣77
俈俈丏僞僀儖偺栤戣
偨偰丄傛偙偺挿偝偑偦傟偧傟丂9cm丄13cm偺挿曽宍偺僞僀儖傪丄壓偺恾偺傛偆偵丂1cm偁偗偰丄 惓曽宍偵暲傋傑偟偨丅暲傋偨僞僀儖偼丄傕偭偲傕彮側偔偟偨偲偒壗枃偱偡偐丅
嶼悢100偺擄栤丒婏栤
拞懞媊嶌
島択幮僽儖乕僶僢僋僗
乮憗堫揷拞乯
乮儁儞僱亅儉丗偽傫偪傖傫乯
嵟弶偵廲曽岦傪峫偊傑偡丅
僞僀儖偺枃悢傪俶偲偡傞偲丄廲曽岦偺挿偝偼丂俋俶亄俶亅侾丂偲側傝傑偡丅
俶傪侾偐傜弴偵戙擖偡傞偲
俋丄侾俋丄俀俋丄俁俋丄係俋丄俆俋丄俇俋丄丒丒丒偲側傝傑偡丅
偙偺寢壥偐傜暘偐傞偙偲偼戞侾埵偼俋偱偁傞丅
偦傟埲奜偼慡偰偑弌尰偡傞丅乮屘偵丄戞侾埵偩偗峫偊傟偽椙偄乯
師偵墶曽岦傪峫偊傑偡
僞僀儖偺枃悢傪摨偠偔俶偲偡傞偲丄墶曽岦偺挿偝偼丂侾俁俶亄俶亅侾丂偲側傝傑偡丅
俶傪侾偐傜弴偵戙擖偡傞偲
侾俁丄俀俈丄係侾丄俆俆丄俇俋丄丒丒丒偲側傝傑偡丅
偙偺寢壥偐傜暘偐傞偙偲偼憹暘偼侾係偱偁傞丅
偙偙偱戞侾埵偩偗傪峫偊偰傒傞偲
俁丄俈丄侾丄俆丄俋丄俁丄丂偲側傝俆夞偱尦偵栠傝傑偡丅
寢榑
墶曽岦偺挿偝偺戞侾埵偑俋偺応崌偼慡偰惓曽宍偵側傞丅
墶曽岦偱戞侾埵偑俋偵側傞偺偼僞僀儖偑俆偺攞悢偺応崌偱偁傞丅
屘偵丄嵟彫枃悢偼墶曽岦偑俆枃偺応崌偱偁傞丅乮挿偝偼俇俋偲側傞乯
廲曽岦偑俇俋偺帪偼俈枃昁梫偱偡丅
廬偭偰僞僀儖枃悢偼俆亊俈亖俁俆枃偱偁傞丅
埲壓丄惓曽宍偵側傞働乕僗偼
墶曽岦偑俆偺惍悢攞乮俆丄侾侽丄侾俆丄俀侽丄丒丒丒乯偺帪偱
廲曽岦偼俈偺惍悢攞乮俈丄侾係丄俀侾丄俀俉丄丒丒丒乯偺帪偱偁傞丅

乮儁儞僱亅儉丗teki乯
摎偊丂俁俆枃乮廲俈枃亊墶俆枃乯
亙夝朄亜
廲値枃亊墶倣枃傪暲傋偨応崌偺廲墶偺挿偝偼丄偦傟偧傟丄侾侽値-侾丄侾係倣-侾偲側傝傑偡丅
偙傟傪偙偺傑傑侾侽値-侾亖侾係倣-侾偲偟偰夝偄偰傕丄侾侽偲侾係偺嵟戝岞栺悢偺俀偱妱偭偰値亖俈丄倣亖俆偑媮傑傞偺偱偡偑丄傕偭偲彫妛惗揑偵夝偙偆偲偡傞偲丄廲偺挿偝偺侾偺埵偵拝栚偡傞偙偲偱丄彫妛惗掅妛擭偺恖偵傕夝偗傑偡丅
廲偺挿偝偼侾侽値-侾偱偡偺偱丄侾偺埵偼昁偢俋偱丄偟偐傕慡偰偺侾偺埵偑俋偺帺慠悢偑
奩摉偡傞偙偲偑夝傝傑偡丅
廬偭偰丄侾係倣亅侾偺侾偺埵傪俋偵偡傞嵟彫偺倣傪媮傔傟偽偄偄偙偲偵側傝傑偡丅
傛偭偰丄倣亖俆丄偙偺帪丄値亖俈偱丄枃悢偼俆亊俈亖俁俆枃偱偡丅

乮儁儞僱亅儉丗mhayashi乯
偨偰偵 x 枃丆傛偙偵 y 枃暲傋傞偲偡傞偲

乮儁儞僱亅儉丗kiyo乯
偨偰丂倃枃丂傛偙丂倄枃丂偲偡傞丅
俋*倃+乮倃-侾乯亖侾俁*倄+乮倄-侾乯
丂丂丂丂丂丂丂丂倄亖乮俆/俈乯*倃
丂嵟彫偼丄倃亖俈丂倄亖俆
丂摎偊丂俁俆枃丅

乮儁儞僱亅儉丗傗側偣乯
栤戣偺傑傑偺恾幃偱偍摎偊偟傑偡偹
廲偺挿偝偼丂俋們倣亊悢俙亄俙亅侾亖侾侽俙亅侾偵側傝傑偡
墶偺挿偝偼丂侾俁們倣亊悢俛亄俛亅侾亖侾係俛亅侾偵側傝傑偡
惓曽宍偭偰帠側偺偱
丂丂丂侾侽俙亅侾亖侾係俛亅侾
丂丂丂侾侽俙亖侾係俛
傕偭偲傕彮側偄悢偭偰偙偲側偺偱媗傑傞偲偙傠
侾侽偲侾係偺嵟彫岞攞悢傪媮傔侾們倣傪堷偗偽
惓曽宍偺堦曈偺挿偝偵側傝傑偡
乮嵟彫岞攞悢偺媮傔曽偼偲偽偟偪傖偄傑偡偹乯
偙偙偐傜惓曽宍偺曈偺挿偝偼俇俋們倣
僞僀儖偺悢偼廲俇俋亐俋亖俈梋傝俇
墶偼俇俋亐侾俁亖俆梋傝係
崌寁偼俈亊俆亖俁俆
嵟廔摎偊俁俆枃偱偡丅

乮儁儞僱亅儉丗嶰妏掕婯乯
乻夝乼
僞僀儖傪丄廲偵倣枃丄墶偵値枃暲傋傞偲偡傞偲丄
惓曽宍偺廲偺挿偝偼丄俋倣亄倣亅侾丂乧嘆
丂丂丂丂墶偺挿偝偼丄13値亄値亅侾丂乧嘇
惓曽宍偵側傞偺偩偐傜嘆嘇偼摍偟偔丄
丂丂10倣亖14値丂亪 俆倣亖俈値丂丂 乧嘊
嘊傪枮偨偟丄倣値偑嵟傕彫偝偔側傞偺偼BR>
丂丂倣亖俈丆値亖俆 偺丂倣値亖35丂 乧乵摎乶

乮儁儞僱亅儉丗岼偺柌乯
愝抲偡傞僞僀儖偺墶偺枃悢傪倶丄廲偺枃悢傪倷偲偡傞偲丄慡懱偺宍偑惓曽宍偵側傞偺偱
丂丂丂丂14(x-1)亄13 亖 10(y-1)+9 偑惉棫偡傞丅
偙偺曽掱幃傪夝偔偲丄
7x = 5y偲側傝丄x傪枮偨偡嵟彫偺惍悢偼 x = 5 丄y = 7偲側傞丅
場偭偰媮傔傞枃悢偼 xy = 35 枃偱偁傞丅

乮儁儞僱亅儉丗奰杮丂峗乯
廲偵値枃偺僞僀儖傪暲傋偨帪偺崅偝傪峫偊傞偲
傑偢僞僀儖偺崅偝偺崌寁偼丂僞僀儖偺崅偝亊枃悢丂亖丂俋亊値丂[們倣]
偦偟偰僞僀儖偲僞僀儖偺娫偵偼侾們倣偢偮偺寗娫偑偁偗偰偁傝
偦偺寗娫偺悢偼丂僞僀儖偺枃悢亅侾丂偲側傞偨傔
寗娫偺崅偝偺崌寁偼丂寗娫偺崅偝亊寗娫偺悢丂亖丂侾亊乮値亅侾乯丂亖丂値亅侾[們倣]
傛偭偰慡懱偲偟偰偺崅偝偼
僞僀儖偺崅偝崌寁亄寗娫偺崅偝崌寁丂亖丂俋値亄値亅侾丂亖丂侾侽値亅侾[們倣]
摨條偵墶偵倣枃偺僞僀儖傪暲傋偨帪偺暆偼
丂丂丂乮侾俁亊倣乯亄乮倣亅侾乯丂亖丂侾係倣亅侾[們倣]
僞僀儖偺暲傃偑惓曽宍偵側傞丄懄偪廲墶偺挿偝偑堦抳偡傞
丂丂丂侾侽値亅侾丂亖丂侾係倣亅侾
偺幃傪枮偨偡嵟彫偺値丆倣偼
値亖俈丂丆丂倣亖俆丂偲側傝
廲偵俈枃丄墶偵俆枃偱丂俈亊俆丂亖丂俁俆[枃]丂暲傋偨応崌偵
俇俋們倣丂亊丂俇俋們倣丂偱嵟傕彫偝偄惓曽宍偲側傞帠偑暘偐傞丅

乮儁儞僱亅儉丗偨偗偖傒偺斣乯
廲偺枃悢傪倶丂墶偺枃悢傪倷偲偡傞偲廲偲墶偺挿偝偑摍偟偔丄寗娫偼憃曽偺枃悢傛傝偦傟偧傟侾売強彮側偄偨傔丄
丂丂丂9x+(x-1)=13y+(y-1)
丂丂丂10x-1=14y-1
丂丂丂10x=14y
丂丂丂5x=7y
俆偲俈偺嵟彫岞攞悢亖俁俆
傛偭偰丂x=7丂y=5丂x亊y亖7亊5=35

乮儁儞僱亅儉丗shihants乯
X傪廲偵暲傋傞僞僀儖偺悢丄Y傪墶偵暲傋傞僞僀儖偺悢偲偡傞偲丄
廲偺曈偲墶偺曈偑摍偟偄応崌偼丄
丂丂丂9X+(X-1)=13Y+(Y-1)
偲側傞丅乮X-1,Y-1偼偦傟偧傟僞僀儖偺娫偺侾們倣偺暆傪昞偡丅乯
偙傟傪娙扨偵偡傞偲丄Y=(5/7)X偲側傞丅
僌儔僼傪昤偔偲娙扨偩偑丄偙偺幃偱X,Y偑椉曽惓偺惍悢偵側傞傕偭偲傕掅偄揰偼(7,5)偱偁傞丅
傛偭偰丄廲偵幍枃丄墶偵屲枃暲傋傟偽偄偄偺偱丄7x5=35偱丄35枃丅
9x7+6=69,13x5+4=69偱椉曈偼摍偟偔丄惓曽宍偱偁傞偙偲偑妋擣偱偒傞丅

乮儁儞僱亅儉丗Underbird乯
僞僀儖傪墶偵m枃丄廲偵値枃暲傋偨偲偡傞偲丄
墶偼丄13*m+(m-1)丄廲偼丄9*n+(n-1)傛傝
丂丂14*m-1=10*n-1
丂丂7*m=5*n
傛偭偰丄m=5*k , n=7*k (k=1,2,3....)偲側傞偺偱
嵟傕彮側偄枃悢偼m=5 , n=7傛傝
35枃丒丒丒乮偙偨偊乯

乮儁儞僱亅儉丗怣嶰乯
僞僀儖偺宍傪廲墶偦傟偧傟侾偢偮戝偒偔偟偨傕偺傪峫偊傞偲丄偙傟傪枾拝偟偰晘
偒媗傔偰惓曽宍傪嶌傞栤戣偵側傝傑偡丅墶侾係丄廲侾侽偺僞僀儖傪墶偵壗枃偐暲
傋偨挿偝偲丄廲偵壗枃偐暲傋偨挿偝偑摍偟偔側傞挿偝偼丄侾係偲侾侽偺嵟彫岞攞
悢偲側傝傑偡丅偙傟偼俈侽偱偡丅廬偭偰丄墶偵俆枃丄廲偵俈枃暲傇偙偲偵側傝丄
慡晹偱俁俆枃巊偄傑偡丅側偍丄弌棃忋偑傞惓曽宍偺曈偺挿偝偼丄俇俋乮僙儞僠乯
偵側傝傑偡丅

乮儁儞僱亅儉丗儕僫儔僀乯
傑偢丄廲墶憃曽偺挿偝偑婔偮偵側傞偐偲尵偆偲丄廲偵暲傋傞僞僀儖偺枃悢傪値丄墶偵暲傋傞僞僀儖偺枃悢傪倣偲偡傞偲
丂丂丂廲乧乧9値乮僞僀儖偩偗偵偟偨帪偺挿偝乯+値-侾乮寗娫偺挿偝乯亖10値-侾
丂丂丂墶乧乧13倣乮僞僀儖偩偗偵偟偨帪偺挿偝乯+倣-1乮寗娫偺挿偝乯亖14倣-1
偲側傝傑偡惓曽宍偵暲傋傞偨傔偵
丂丂丂10値-1亖14倣-1
丂丂丂10値亖14倣
丂丂丂俆値亖7倣
傛偭偰丄僞僀儖偺枃悢偑嵟彫偵側傞偺偼値亖俈丄倣亖俆
7亊俆亖35枃暲傋傟偽椙偄栿偱偡

乮儁儞僱亅儉丗yokodon乯
戣堄偺僞僀儖傪墶偵 x 枃丄廲偵 y 枃暲傋偰丄戣堄偺傗傝曽偱惓曽宍傪嶌傞偙偲傪
峫偊傑偡丅
1 m 偺偡偒娫偑丄墶偵偼 x - 1 儢強丄廲偵偼 y - 1 儢強弌棃傞偺偱丄曈偺挿偝偵
娭偟偰丄
丂丂丂13x + (x - 1) 亖 9y + (y - 1)
偑惉傝棫偪傑偡丅偙傟傪惍棟偟偰丄
丂丂丂7x 亖 5y
偲側傝傑偡丅偙傟傪枮偨偡帺慠悢 x, y 偺嵟彫抣偺慻傒崌傢偣偼
丂丂丂(x, y) 亖 (5, 7)
偱偡丅廬偭偰丄媮傔傞枃悢偼 5亊7 亖 35 枃乧乮摎乯丄偱偡丅
僥乕儅偼丄惍悢偺乽屳偄偵慺乿偱偟傚偆偐丠

乮儁儞僱亅儉丗儌儖儌僢僩戝恇乯
戣堄偐傜廲9cm,墶13cm偺僞僀儖傪廲偵X枃丄墶偵Y枃(X,Y偼帺慠悢)暲傋傞偲偡傞偲
廲偺挿偝偼9X+1亊(X-1)=10X-1丄墶偺挿偝偼 13Y+1亊(Y-1)=14Y-1
惓曽宍偲側傞偙偲偐傜廲亖墶偩偐傜 10X-1= 14Y-1
傛偭偰10X=14Y偐傜X=7Y/5傛傝嵟彫偺Y亖5丄偙偺帪X=7
埲忋傛傝媮傔傞枃悢偼5亊7=35
摎 35枃

乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
摎偼丄俁俆枃偱偡丅
暲傋廔傢偭偨忬懺偺僞僀儖偺枃悢傪偨偰倎枃丄傛偙倐枃偲偟傑偡丅
偡傞偲惓曽宍偺堦曈傪偨偰偱峫偊傞偲丄僞僀儖偺偨偰偺挿偝偑俋cm丄僞僀儖偲僞
僀儖偺娫偑 乮倎亅侾乯 屄偁傞偺偱丄
俋倎亄乮倎亅侾乯亖侾侽倎亅侾 cm丂偱偡丅
摨條偵傛偙偱峫偊傞偲丄僞僀儖偺傛偙偺挿偝偑侾俁cm丄僞僀儖偲僞僀儖偺娫偑
乮倐亅侾乯屄偁傞偺偱丄
侾俁倐亄乮倐亅侾乯亖侾係倐亅侾 cm 偱偡丅
偙偺擇偮偺挿偝偑摍偟偄偺偱丂侾侽倎亅侾亖侾係倐亅侾
惍棟偡傞偲丂俆倎亖俈倐
偙偺曽掱幃傪枮偨偡嵟彫偺帺慠悢偼丄俆偲俈偑屳偄偵慺側偺偱丄乮俈丆俆乯偲側
傝傑偡丅
傛偭偰嵟彫偺枃悢偼丂俈亊俆亖俁俆丂枃偱偡丅

乮儁儞僱亅儉丗昹揷丂柧枻乯
廲俈丆墶俆丆曈偺挿偝俇俋丆枃悢俁俆枃偲側傝傑偡丏
Option Explicit
Const A As Integer = 9
Const B As Integer = 13
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = "廲"
Cells(1, 2).Value = "墶"
Cells(1, 3).Value = "挿偝"
Cells(1, 4).Value = "枃悢"
Range("D2").Select
'
Dim tate As Integer
Dim yoko As Integer
Dim tate_nagasa As Integer
Dim yoko_nagasa As Integer
Dim owari As Integer
yoko = 1
tate = 1
yoko_nagasa = B
tate_nagasa = A
owari = 0
While owari = 0
If yoko_nagasa < tate_nagasa Then
yoko = yoko + 1
yoko_nagasa = yoko_nagasa + 1 + B
ElseIf tate_nagasa < yoko_nagasa Then
tate = tate + 1
tate_nagasa = tate_nagasa + 1 + A
Else
owari = 1
End If
Cells(2, 1).Value = tate
Cells(2, 2).Value = yoko
Cells(2, 3).Value = tate_nagasa
Cells(2, 4).Value = tate * yoko
Wend
End Sub
Sub Macro2()
Sheets("Sheet2").Select
Cells(1, 1).Value = "廲"
Cells(1, 2).Value = "墶"
Cells(1, 3).Value = "挿偝"
Cells(1, 4).Value = "枃悢"
Cells(1, 5).Value = 0
Range("D2").Select
'
Dim tate As Integer
Dim yoko As Integer
Dim tate_nagasa As Integer
Dim yoko_nagasa As Integer
Dim owari As Integer
yoko = 1
tate = 1
yoko_nagasa = B
tate_nagasa = A
owari = 0
While owari = 0
If yoko_nagasa < tate_nagasa Then
yoko = yoko + 1
yoko_nagasa = yoko_nagasa + 1 + B
ElseIf tate_nagasa < yoko_nagasa Then
tate = tate + 1
tate_nagasa = tate_nagasa + 1 + A
ElseIf tate <= 200 Then
Cells(1, 5).Value = Cells(1, 5).Value + 1
Cells(Cells(1, 5).Value + 1, 1).Value = tate
Cells(Cells(1, 5).Value + 1, 2).Value = yoko
Cells(Cells(1, 5).Value + 1, 3).Value = tate_nagasa
Cells(Cells(1, 5).Value + 1, 4).Value = tate * yoko
yoko = yoko + 1
yoko_nagasa = yoko_nagasa + 1 + B
tate = tate + 1
tate_nagasa = tate_nagasa + 1 + A
Else
owari = 1
End If
Wend
End Sub

乮儁儞僱亅儉丗忨偺偍偠偝傫乯
墶13cm偺僞僀儖傪n枃暲傋偨帪偺挿偝偼丄14n-1丂cm
廲9cm偺僞僀儖傪n枃暲傋偨帪偺挿偝偼丄10n-1丂cm
| 枃悢 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 10 | ゥ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 墶 | 13 | 27 | 41 | 55 | 69 | 83 | 97 | 111 | 125 | 139 | 14n-1 |
| 廲 | 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 | 10n-1 |
偙偺応崌惓曽宍偲側傞偺偼丄廲偺挿偝偺壓堦寘偑俋偲側傞偙偲偑傢偐傝傑偡偺偱丄
墶偺挿偝偑壓堦寘栚俋偲側傞枃悢傪寁嶼偟傑偡丅忋偺昞偐傜尒偰傕俆枃偲傢偐傝傑偡丅
廬偭偰摎偊偼丄墶俆枃丄廲俈枃丄巊梡枃悢偼俆亊俈亖俁俆枃偲側傝傑偡丅
惓曽宍偲側傞巊梡枃悢偼師偺捠傝偱偡丅
| 丂 | 侾 | 俀 | 俁 | 係 | 俆 | 丒丒丒 | 値 |
|---|---|---|---|---|---|---|---|
| 墶巊梡枃悢 | 5 | 10 | 15 | 20 | 25 | 丒丒丒 | 5n |
| 廲巊梡枃悢 | 7 | 14 | 21 | 28 | 35 | 丒丒丒 | 7n |
| 憤巊梡枃悢 | 35 | 140 | 315 | 560 | 875 | 丒丒丒 | 35n2 |

乮儁儞僱亅儉丗僥儌乯
Excel偱夝偒傑偟偨丅
彫偝偄弴偵
丂丂丂1斣栚偼丂俆亊俈亖俁俆
丂丂丂俀斣栚偼侾侽亊侾係亖侾係侽
丂丂丂俁斣栚偼侾俆亊俀侾亖俁侾俆
丂丂丂丒
丂丂丂丒
丂丂丂俶斣栚偼俁俆亊俶亊俶
Excel丂偼悢妛傪夝偔忋偱旕忢偵嫮椡側僣乕儖偵側傝傑偡偑丄
堦曽梋傝峫偊側偔偰傕嵪傓偺偱丄偪傚偭偲暰奞偑偁傞偐傕抦傟傑偣傫丅
側傞傋偔墧昅傪帩偭偰愄偐傜偺傗傝曽偱夝偔曽偑摢偺堊偵偼椙偄偐傕偟傟傑偣傫丅

乮儁儞僱亅儉丗Toru乯
恾偺傛偆偵偲偄偆偙偲偱丄僞僀儖偺岦偒偼堦掕偲峫偊偰丄廲偵M屄丄墶偵N屄丄暲傋傞
偲峫偊傞偲丄廲偺挿偝偼丄偡偒娫偺乮M亅侾乯cm傪壛偊偰
丂丂丂俋M亄乮M亅侾乯亖侾侽M亅侾乮cm乯
墶偺挿偝偼摨條偵
丂丂丂侾俁N亄乮N亅侾乯亖侾係N亅侾乮cm乯
偙傟偑惓曽宍偵側傞偨傔偵偼丄
丂丂丂侾侽M亅侾亖侾係N亅侾
傛傝丄M亖俈N乛俆傛偭偰N偼俆偺攞悢偱嵟彫偼N亖俆丄
偙偺帪M亖俈傛偭偰媮傔傞僞僀儖偺悢偼俆亊俈亖俁俆屄亅亅亅亅亅摎偊
惓曽宍偲偺偙偲偱丄偡偒娫偑偁偭偰傕憡嶦偝傟偰偟傑偭偰丄栤戣偵側傜側偄偱偡偑丄
挿曽宍側傜偳偆偐偲偄偆偙偲傪彮偟峫偊偰傒傑偟偨丅
廲丗墶亖倎丗倐乮倎丆倐偼惓偺惍悢偱屳偄偵慺乯偲偟偰傒傞偲丄
丂丂丂乮侾侽M亅侾乯丗乮侾係N亅侾乯亖倎丗倐傛傝侾係倎N乗侾侽倐M亖倎亅倐
偙偺晄掕曽掱幃偑惍悢夝傪帩偮忦審傪峫偊傞偲丄倎亅倐偼俀偺攞悢偩偐傜丄倎丄倐偲傕偵嬼悢偁傞偄偼婏悢偩偑丄倎丄倐屳偄偵慺偱偁傞偐傜丄嬼悢偼戣堄偵崌傢偢丄偲傕偵婏悢丄倎偑俆偺攞悢偺帪丄倎亅倐傕俆偺攞悢偲側傝丄傛偭偰倐傕俆偺攞悢偲側偭偰晄揔丄倐偑俈偺攞悢偺帪傕摨條偵晄揔丅媡偵倎丄倐偲傕偵婏悢丄倎偼俆偺攞悢偱側偔丄倐偼俈偺攞悢偱側偄偲偡傟偽俈倎偲俆倐偼屳偄偵慺側偺偱丄
忋偺晄掕曽掱幃乮偺慡懱傪俀偱妱偭偨傕偺乯偼昁偢惍悢夝傪傕偮丄偙偺侾偮傪乮No,俵o乯偲偡傟偽(No+5bt, 俵o+7at) (t偼惍悢)傕夝偲側傞偺偱丄昁偢惓偺惍悢夝偺慻傪傕偮丅
偨偲偊偽倎亖俁丄倐亖俆偲偟偰峫偊偰傒傞偲丄俀俆M亅俀侾N亖侾丂俵亅俶亖N乫丂偲
偡傞偲係M亄俀侾N乫亖侾丂峏偵M亄俆N乫亖M乫偲偡傞偲係M乫亄N乫亖侾傛偭偰M乫亖侽丄
N乫亖侾偼戣堄傪枮偨偟丄偙傟偐傜媡偵寁嶼偟偰丄M亖亅俆丄俶亖亅俇丄堦斒夝偼
丂丂丂乮M,N乯亖乮俀侾倲亅俆,俀俆倲亅俇乯
傛偭偰偙偺応崌偺嵟彫偺僞僀儖偺悢偼倲亖侾偲偟偰侾俇亊侾俋亖俁侽係

乮儁儞僱亅儉丗壖柺倃乯
廲偲墶偵侾們倣偢偮偨偟偰丄侾侽偲侾係偺嵟彫岞攞悢俈侽偐傜
俈侽亐侾侽亖俈丄俈侽亐侾係亖俆丄俈亊俆亖俁俆
摎丂丂俁俆枃

乮儁儞僱亅儉丗kirkland乯
| 俙孨 | 乽偙傫側偺丄幚嵺偵彂偄偰偄偗偽妝彑偠傖側偄偱偡偐両乿 |
| 愭惗 | 乽寁嶼偱傗傟両乿 |
| 俙孨 | 乽寗娫偺埖偄曽偑柺搢偱偡傛丅僞僀儖偺悢偲寗娫偺悢偑堘偆偟丅乿 |
| 愭惗 | 乽偦傠偊傠両乿 |
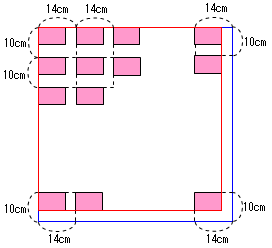
| 俙孨 | 乽偍乕偭丄僫僀僗傾僀僨傿傾両傕偆侾偮梋暘偵寗娫傪嶌傟偽偄偄傫偱偡偹丅亂壓恾亃 廲墶侾們倣偢偮偺偽偟偰傕惓曽宍偱偡偟丄偙傟偩偲丄廲10們倣丄墶14們倣偺挿曽宍傪侾偐偨傑傝偲峫偊傞偙偲偑偱偒傑偡偹丅10偲14偺嵟彫岞攞悢偼70偩偐傜丄偺偽偟偰偱偒傞惓曽宍偺堦曈偼70們倣偱偡丅偙偺偲偒丄10們倣亊14們倣偺挿曽宍偼丄廲偵俈屄丄墶偵俆屄暲傇偺偱丄崌寁35枃偱乣偡丅乿 |
| 愭惗 | 乽惓夝偩両乿 |
| 俙孨 | 乽側傫偐丄崱擔偼偛婡寵側側傔偱偡偹丅乿 |
| 愭惗 | 乽埨寍擳搰偑堷戅偟偰棊偪崬傫偱偄傞傫偩両乿 |
| 俙孨 | 乽壗導偵偁傞搰偱偡偐丠乿 |

乮儁儞僱亅儉丗Y.M乯
廲偵x枃丄墶偵y枃暲傋偨偲偟傑偡丅
忦審傛傝丄
丂丂丂9x+(x-1)=13y+(y-1)丂
偑惉傝棫偪丄偙傟傪惍棟偡傞偲丄
丂丂丂10x-1=14y-1
丂丂佁10x=14y丂
丂丂佁x:y=7:5
偲側傝傑偡丅
僞僀儖偺枃悢x,y偼嫟偵帺慠悢側偺偱丄
廲偵7枃丄墶偵5枃丄懄偪寁35枃暲傋傞偲丄
嵟彫偺枃悢偱惓曽宍偑惉棫偟傑偡丅
丂丂丂摎偊丗35枃
丄偲壗偐拞妛揑側夝偒曽偩偭偨偺偱偱偒傞偩偗彫妛峑偺斖埻偱夝偄偰傒傑偟偨伀
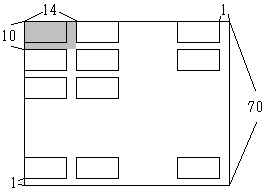
忋偺恾偺傛偆偵"廲10丄墶14"偺壦嬻偺僞僀儖偱峫偊偰傒傑偡丅
偡傞偲丄10偲14偺嵟彫岞攞悢傪偲偭偰 70丅
懄偪1曈70cm(幚嵺偼1曈69cm偱偡)偺惓曽宍偑丄嵟彫偺惓曽宍偲偄偆偙偲偵側傝傑偡丅
偟偨偑偭偰丄
丂丂丂(70亐10)亊(70亐14)=35
摎偊丗35枃
壗偐傢偐傝恏偄偱偡偹乧(徫

乮儁儞僱亅儉丗屵擭偺偆傝傏偆乯
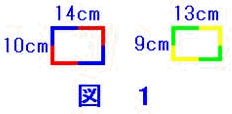
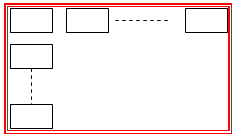
僞僀儖偺巊梡枃悢偺傒傪摎偊傞偺偱偁傞偐傜丄俋們倣亊侾俁們倣偺挿曽宍偺僞僀儖乮恾侾塃乯傪暲傋傞偙偲傪峫偊傞偺偱偼側偔丄侾侽們倣亊侾係們倣偺挿曽宍偺僞僀儖乮恾侾嵍乯傪暲傋傞偙偲偵傛傝丄寗娫偺侾們倣乮恾俀乯傪杽傔偰丄寗娫側偔暲傋傞乮恾俁乯偙偲傪峫偊傞丅
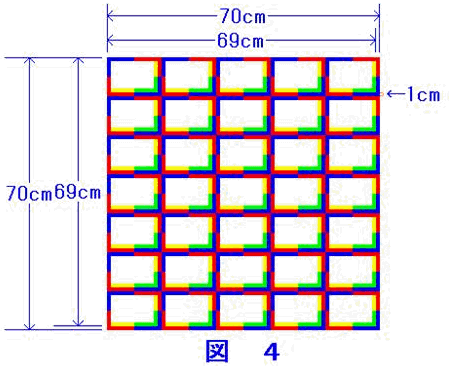
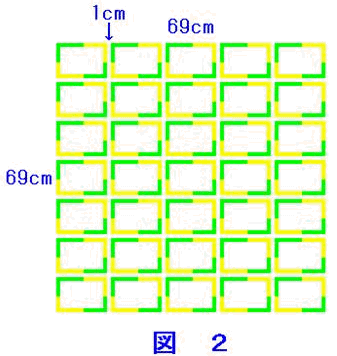 偙偺傛偆偵偟偰傕丄恾俁傪恾俀偵廳偹偨恾
係傛傝傕柧傜偐偱偁傞偑丄媮傔傞摎偊偼曄傢傜側偄丅
偙偺傛偆偵偟偰傕丄恾俁傪恾俀偵廳偹偨恾
係傛傝傕柧傜偐偱偁傞偑丄媮傔傞摎偊偼曄傢傜側偄丅
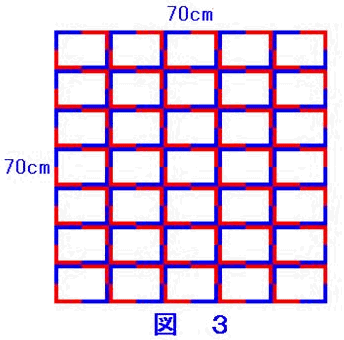
傛傝彮側偄枃悢偱僞僀儖傪惓曽宍偵暲傋傞
偺偱偁傞偐傜丄侾侽偲侾係偲偺嵟彫岞攞悢傪
傑偢媮傔傞丅
丂丂侾侽亖俀亊俆
丂丂侾係亖俀丂丂亊俈傛傝丄
丂丂俀亊俆亊俈亖俈侽
備偊偵丄傛傝彮側偄僞僀儖偱堦曈偑俈侽們倣偺惓曽宍傪嶌傞偙偲偑偱偒傞丅
傛偭偰丄僞僀儖偺巊梡枃悢偼丄
丂丂俈侽亖侾侽亊俈
丂丂俈侽亖侾係亊俆傛傝丄
丂丂俈亊俆亖俁俆乮枃乯丂乧乮摎乯

乮儁儞僱亅儉丗崅嫶丂摴峀乯
崱夞偺夝摎偼乧
14亊10偺僞僀儖傪偡偒傑側偔晘偒媗傔傞偲偄偆偙偲偲摨偠偱偡丅
偙偺偲偒偼侾cm戝偒偄惓曽宍傪摼傞偙偲偵側傝傑偡丅
墶偵x屄丂偨偰偵y屄偺挿曽宍傪暲傋偨偲偒丂墶偺挿偝=廲偺挿偝傛傝
丂丂丂14x=10y偐傜7x=5y
x偑5偺攞悢偱側偗傟偽側傜偢丂x=5k偱偁傜傢偝傟傑偡丅
偙偺偲偒丂y=7k丂偱偁傞偐傜丂嵟彫偺惓偺惍悢偺儁傾偼丂x=5丂y=7偺
偲偒偱偁傝丂僞僀儖偺枃悢偼丂35枃偲側傞丅
偦偺傑傑峫偊傞偲(13+1)x-1=(9+1)y-1偐傜丂丂14x=10y偲丂摨偠幃偵側傝傑偡偹丅

| 岼偺柌 | 昹揷丂柧枻 | kiyo |
| 嶰妏掕婯 | teki | 忨偺偍偠偝傫 |
| 偽傫偪傖傫 | 傗側偣 | 儕僫儔僀 |
| 偨偗偖傒偺斣 | Y.M | 僥儌 |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | Toru | Underbird |
| shihants | 奰杮丂峗 | 崅嫶丂摴峀 |
| 怣嶰 | 儌儖儌僢僩戝恇 | yokodon |
| mhayashi | kirkland | 壖柺倃 |
| 屵擭偺偆傝傏偆 |

乽10値-1亖14倣-1乿偲偄偆曽掱幃偐傜丄俈偲俆偺嵟彫岞攞悢傪摎偊偰偄偨偩偗傟偽偄偄傢偗偱偡偹丅
偲偙傠偑丄壖柺倃丄kirkland偝傫丄Y.M偝傫丄崅嫶丂摴峀偝傫丄 屵擭偺偆傝傏偆偝傫偺夝摎偵偁傝傑偡傛偆偵丄"廲10丄墶14"偺壦嬻偺僞僀儖傪峫偊偰偄偨偩偗傟偽丄柺搢側曽掱幃傪棫偰偢偲傕丄侾係偲侾侽偺嵟彫岞攞悢丄偙傟側傜埫嶼偱偒傑偡偹丅俈侽丄廬偭偰偱偒偁偑偭偨惓曽宍偼侾堷偄偰侾曈偺挿偝偑俇俋cm偱偡丅
乽10値-1亖14倣-1乿偲偄偆幃傪棫偰傜傟偨曽偼丄師偵乽10値亖14倣乿偲偄偆幃曄宍傪偁傞堄枴婡夿揑偵偟偰偄傞偲巚偄傑偡丅椉曈偵侾傪懌偟偰傕摍崋偑惉傝棫偮偲偄偆偙偲偱偡偑丄偙偺幃曄宍偵偼暿偺堄枴偑偁傞乮俆恖偺曽偑側偝偭偨傛偆偵惓曽宍偺奜懁偵暆侾cm偺寗娫傪嶌偭偰峫偊偰傕摨偠偙偲乯 偲偄偆偙偲傪峫偊傞偲丄扨弮側幃曄宍傕幚偼傆偐乕偄堄枴偑偁傞偲偄偆偙偲傪姶偠傑偡丅
傑偨丄Toru偝傫偼挿曽宍偵偮偄偰偺峫嶡傪偟偰偔偩偝偄傑偟偨丅 惓曽宍偵斾傋傞偲忦審偑傓偢偐偟偄偲巚偄傑偡丅 寢壥丄廲墶斾偑擟堄偺挿曽宍傪嶌傞偙偲偑偱偒傞偲偄偆偙偲偱丄 戝曄嫽枴怺偄寢壥偩偲巚偄傑偡丅

 E-mail
E-mail
 栠傞
栠傞
 top
top