Weekend Mathematics/問題/問題75
75.最終結果は?
ある正の整数を計算するとき、次のような決まりがあります。
(整数 → 正の整数 と修正します。ごめんなさい。3/3)
1.その整数が3で割り切れるときは、3で割ります。上の決まりを守って、整数が1になるまで続けます。
2.その整数が3で割り切れないときは、1を足します。
(1)24は何回の計算で1になりますか。
(2)50は何回の計算で1になりますか。
(3)3回の計算で1になる整数をすべてあげなさい。
おまけ
(4)どんな正の整数から始めても、必ず1にたどりつくことを証明しなさい。
パズルより面白い中学入試の算数
ピーター・フランクル
講談社
聖徳中学校'93入試
(ペンネ-ム:瑞樹)
(1)24→8→9→3→1 となり、4回
(2)50→51→17→18→6→2→3→1 となり、7回

(ペンネ-ム:Y.M)
(1)~(3)までは地道に計算しました。
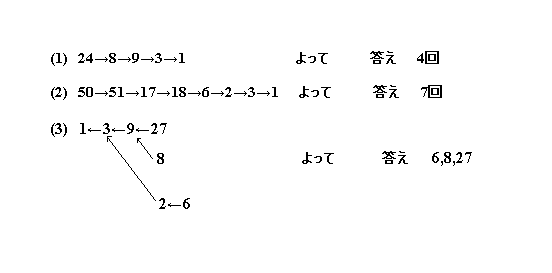
ところで今回の問題と似たような問題が、今学校でやっている問題集の、
千葉大学の問題として出ていました。
こちらは3の倍数ではなく「2の倍数」でしたが・・・。

(ペンネ-ム:teki)
(1) 4回
(2) 7回
(3) 6、8、27
(1)は、24→8→9→3→1 の4回です。
(2)は、50→51→17→18→6→2→3→1 の7回です。
(3)は、3×(3-1)、3×3-1、3×3×3の3つが該当します。

(ペンネ-ム:モルモット大臣)
まず3で÷演算をA, 1を+する 演算をBとします。
(1) A(24)=8→B(8)=9→A(9)=3→A(3)=1の4回の演算で1になります。
(2) B(50)=51→A(51)=17→B(17)=18→A(18)=6→A(6)=2→B(2)=3→ A(3)=1の7回
(3)ここで1に対する演算はもし行うとすればB(1)=2→B(2)=3→A(3)=1と3回で1に戻りま
すが1は最初から演算の最終目標であるので省きます。
そこで逆算をしていきます。3回目で1になるためには2回目の演算結果が3であり3回
目の演算がAである必要があります。このため2回目の演算がAの場合は1回目の演算結
果は9である。また2回目の演算がBの場合は1回目の演算結果は2である必要がありま
す。よって1回目の演算結果の場合は2または9となります。
AまたはBの演算で2または9となれば良いのですから
(1回目の演算結果が2の場合)最終的には3回の演算で1となる数は6, 8, 27である。
Aの演算結果なら最初の数は2×3=6
Bの 演算結果なら最初の数は1であるので1回目で1になるため不適
(1回目の演算結果が9の場合)
Aの演算結果なら最初の数は9×3=27
Bの 演算結果なら9-1=8

(ペンネ-ム:午年のうりぼう)
(1)、(2)
| 整数 | 計算の回数 | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 24 | 8 | 9 | 3 | 1 | |||
| 50 | 51 | 17 | 18 | 6 | 2 | 3 | 1 |
(3)
左図より、3回の計算で1になる整数は、
27,8,6,1 …(答)
です。
(ちなみに、全ての整数を計算した場合でも、答えは上の4つのみです。
?∵ 負の整数でこの計算をやると、(4)より、一度も正の整数が出ないで、最後は0になります。0は3で割り切れるので、1が足せません。?)
(4) Give Up です……?T_T?。

(ペンネ-ム:杖のおじさん)
(1)24→8→9→3→1 4回です。
(2)50→51→17→18→6→2→3→1 7回です。
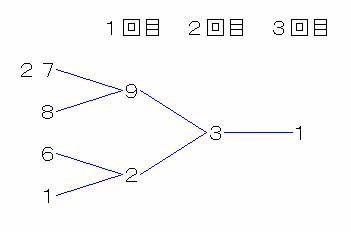
(3)整数nは1以上で1を加算してその整数nになるものと3で割ってその整数nになるものの2通りあります。 図に書くときは、逆に書きますので、1を基点として一方を1を引いて書き、 一方に3をかけて書いていきます。3回目の数字の中で、整数1をこえるものを数えます。
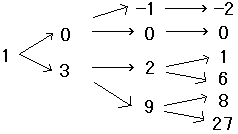
従って、6,8,27です。
(4)整数nを3で割り割り切れるとあまりは0となり、割り切れないとあまりは1または2となります。
割り切れるまで1を加算いたしますので、最終結果は1となります。
どんな整数から始めても必ず1になることは次の様にして確かめました。
| 1 | 2 | 3 | 1 | |||||
| 4 | 5 | 6 | 2 | 3 | 1 | |||
| 7 | 8 | 9 | 3 | 1 | ||||
| 10 | 11 | 12 | 4 | 5 | 6 | 2 | 3 | 1 |
| 13 | 14 | 15 | 5 | 6 | 2 | 3 | 1 | |
| 16 | 17 | 18 | 6 | 2 | 3 | 1 | ||
| 19 | 20 | 21 | 7 | 8 | 9 | 3 | 1 | |
| 22 | 23 | 24 | 8 | 9 | 3 | 1 | ||
| 25 | 26 | 27 | 9 | 3 | 1 | |||
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ||||
| (3n-2) | (3n-1) | 3n | n | ・・・ |
|---|
上の図4列目の数列はnとなっていますので、どんな整数nから始めても1になることが確認できます。

(ペンネ-ム:夢夜(むよ))
(1)まずは実験的に解きましょう。
24>8(1.)>9(2.)>3(1.)>1(1.)
4回ですね。
(2)50>51(2.)>17(1.)>18(2.)>6(1.)>2(1.)>3(2.)>1(1.)
7回ですね。
(3)計算方法は1回につき必ず2通りあります。
ところで、整数は正ですから、3で割る以上は0にならないので、最後は必ず1.が適用されます。
また、(2.)(2.)(1.)の組み合わせに当てはまるのは1しかないので除外します。
よって考えられるのは下の組み合わせです。
8>9(2.)>3(1.)>1(1.)
6>2(1.)>3(2.)>1(1.)
27>9(1.)>3(1.)>1(1.)
ゆえに答えは6、8、27です。
(4)ところで何を証明すればいいのでしょうか?
それは「計算方法で3で割る操作があることから、どんな値も有限回数の計算の後に3で割られて必ず減少し、値は最後に1になる」ことを示せばいいのです。
数学的帰納法で証明します・・・証明中のnは自然数(ただし2以上)とします。
(base)n=2,3の時は下のようにすぐに1になることが確認できます。
2>3(2.)>1(1.)
3>1(1.)
(step)n>3の時にはnをある自然数mを用いて表すと、
n=3m,3m-1,3m-2で表されます。
このとき、nの定義から常にn>mですので有限回の操作でnからmに計算できるかを確認すればいいのです。
(i)n=3mの時(base)(step)より任意の自然数nは全て有限回の計算で値が減少し、必ず1になります。
n=3m>m(1.)
(ii)n=3m-1の時
n=3m-1>3m(2.)>m(1.)
(iii)n=3m-2の時
n=3m-2>3m-1(2.)>3m(2.)>m(1.)
(1)(2)では足す回数(2.の適用回数)は下のようにして求めるのでしょうか。

(ペンネ-ム:wasmath)
まず,問題文についてですが, (4)で必ず1にたどりつくことがはっきりする前に,
「1になるまで(作業を)続ける」というのはおかしいのではないでしょうか?
「1でない限り作業を続け,1になれば作業をやめる」などの表現の方が
適切だと思いますが,いかがでしょう。
(1),(2),(3)をさぼって,(4)だけ解くことにします。
(4) 題意を整理すると,任意の自然数Nに対して,数列{an}を
a1=N, anが3で割り切れるとき an+1=an/3
anが3で割り切れないとき an+1=an+1
で定めるとき, an=1となる自然数nが存在する ・・・・・・(*)
ことを示せばよい。
いま,自然数を
1| 2,3 | 4,5,・・・,9 | 10,・・・
とグループ分けし, m番目のグループに属する自然数が 3m-2より大きく,
3m-1 以下になるようにする。
(m=1のとき3m-2は整数でないが,つじつまは合っている。)
任意の自然数Nに対して
3m-2<N≦3m-1
を満たす自然数mは(Nごとに)必ず存在するので, (*)が成り立つ
ことをこのmについての数学的帰納法で証明する。
1°m=1すなわちN=1のとき(*)が成り立つのは自明。
2°(3m-2,3m-1 ] のとき(*)が成り立つとして,
3m-1<N≦3m とする。 Nは
N=3q+r (qは非負整数, r=0,1,2)
と表される。
r=0のとき,3で割って
3m-2<q≦3m-1
r=1のときは,実際には 3m-1<3q+1≦3m -2 であるから,
3m-2<q+1≦3m-1
r=2のときも同様に, 3m-1<3q+2≦3m -1 より
3m-2<q+1≦3m-1
したがって, 数列{bn}を
r=0のときはb1=q,
r=1,2のときはb1=q+1
bnが3で割り切れるとき bn+1=bn/3
bnが3で割り切れないとき bn+1=bn+3
という規則で定義すると,帰納法の仮定より
bk=1となる自然数k=k(r)が存在する。
このとき
r=0のときn=k(0)+1
r=1のときn=k(1)+3
r=2のときn=k(2)+2
とすれば, an=1であるから (3m-1,3m ] でも(*)は成り立つ。
1°2°より題意は示された。
(おわり)

(ペンネ-ム:スチューデント)
(1)24→8→9→3→1 よって4回
(2)50→51→17→18→6→2→3→1 よって7回
(3)A→B→3→1の順で変わってきている。
ここで、Bには3で割るか1を足して3になる数なので、9と2のどちらかが入る。
(ⅰ)Bが9のとき…うえと同様の理由で27と8 (ⅱ)Bが2のとき…同じく1か6。ここで、1はになった場合はそこで計算が終わるので1は不可。
(ⅰ)Mが3の倍数のとき(ⅰ)、(ⅱ)より、条件を満たさない最小の正の整数Mは存在しない。ゆえにすべての正の整数は、これを満たす。
3で割った、変形後をM’とすると、M>0より、M>M’
ここで、M’が条件を満たすとすると、Mも条件を満たすので、Mが条件を満たさないという仮定に反する。逆にM’が条件を満たさないとすると、Mが条件を満たさない最小の正の整数であるという仮定に反する。よってこの時Mは存在しない。
(ⅱ)Mが3で割ると1か2余る場合。
まずは操作によってMは3の倍数まで1を足される。これを行って3の倍数となったものをM”とすると、M”=M+2(または+1)/3だから、M>1のときM>M”。
(α)M>1のとき、
ここで、M”が条件を満たすとすると、Mも条件を満たすので、Mが条件を満たさないという仮定に反する。逆にM”が条件を満たさないとすると、Mが条件を満たさない最小の正の整数であるという仮定に反する。よってこの時Mは存在しない。
(β)M=1のとき、
1は条件を満たしているので、Mが条件を満たさないという仮定に反する。

(ペンネ-ム:バレー部)
(1)24→8→9→3→1 で4回です。
(2)50→51→17→18→6→2→3→1 で7回です。
(3)1になるためには、3のときに3で割られるしかないので、
まず最後に「3→1」となるのがわかります。ここから逆算していきました。
となるので、6と8と27です。
(4)すべての数は以下の3つに分類できる。
n≡0(mod 3)・・・①②、③の場合も、
n≡1(mod 3)・・・②
n≡2(mod 3)・・・③
n+2≡0(mod 3) もしくは、となるので、1を足していくと3でわりきれます。
n+3≡0(mod 3)

(ペンネ-ム:仮面X)
(1)4回
(2)7回
最大は9と3を通過する27、最小は3だけを通過する6です。あとは、たす1で9を通過する8です。9を通過するのは他にはありません。3だけを通過するのは6だけです。
(3)6,8,27
(4)割り終わった後で1番大きくなるのは、1を2回たしてから3で割るときです。2以上の数に2を足してから3で割ると、元の数より小さくなります。元の数の1より大きい部分を3等分した2つを、2つの1にあげるからです。計算を続けていくとどんどん小さくなって1になります。
全部暗算でやりました。当たってるかな~?

(ペンネ-ム:リナライ)
解答:条件の1、2をそれぞれx、yと置きます
(1)24は3の倍数ですので
24÷3=8(x)
8は3の倍数ではありませんが、+1(y)した9は3の倍数なので
9÷3=3(x)
3は当然3の倍数なので
3÷3=1(x)
よって、xyxxの順番ですので、1になるには計4回
(2)50は3で割りきれませんが、+1(y)した51は3で割りきれますので
51÷3=17(x)
17も3で割りきれませんが、+1(y)すると18で割りきれます。
18÷3=6(x)
6も割りきれるので
6÷3=2(x)
2は3より少ないので、当然3では割りきれません。
よって+1(y)して3になり
3÷3=1(x)
よってyxyxxyxの順番で計7回
(3)3回の計算となる順列は
xxx、xxy、xyx、yxx、xyy、yxy、yyx、yyy
の8通りあります。これをそれぞれxの時×3、yの時-1すると
xxx……1×3×3×3=27上の8つを逆算すると、0の時は1回yをするだけでいいので、これも除外
xxy……1×3×3-1=8
xyx……(1×3-1)×3=6
yxx……(1-1)×3×3=0
xyy……1×3-1-1=1
yxy……(1-1)×3-1=-1
yyx……(1-1-1)×3=-3
yyy……1-1-1-1=-2
おまけの(4)
yを2回繰り返す間に、必然的にxを行う「3で割りきれる」条件を満たすので、常にxは行われます。
例えば、整数zがあるとすると、z、z+1、z+2の中に、必ず一つ3で割りきれる数があります。
また、自然数を3で割ると、必ず数は1に近くなります。
よって、回数に制限が無い限り、正の整数は1に辿りつく事ができます

(ペンネ-ム:figo)
(1) 4回
(2) 7回
(3) 6,8,27
(4) 正数を1でない数xとする(1は計算の必要がないので)
(i)xが3で割り切れる時
xに2の計算をするとxより小さい数が得られる。
(ii)xを3で割った余りが1の時
xに1の計算を2回施し、2の計算をするとxより小さい数が得られる。なぜなら
x>(x+2)/3
3x>x+2
2x>2
x>1
であるので。
(iii)xを3で割った余りが2の時
xに1の計算を1回施し、2の計算をするとxより小さい数が得られる。なぜなら
x>(x+1)/3
3x>x+1
2x>1
x>1/2
であるので。
(i)(ii)(iii)より、計算を繰り返すといくらでも小さい正数が得られる。1は最も小さい正数であるので、必ず1にたどり着く。

(ペンネ-ム:理一郎坊ちゃん)
3で割る操作を/、1を足す操作を+とかくことにする。その右に結果をかく。
(1)24/8+9/3/1 よって、4回。
(2)50+51/17+18/6/2+3/1 よって、7回。
(3)A#B$3/1 となるAを求める。#、$は操作/または+である。
#$=++、+/、/+、//の4通り考えられる。
式を逆にたどると、#$=++のとき、1/3+2+1で、A=1。これは題意に相応しくない。
#$=+/のとき、1/3/9+8で、A=8
#$=/+のとき、1/3+2/6で、A=6
#$=//のとき、1/3/9/27で、A=27 以上3通り。
(4)すべての正整数は、3の倍数か、3の倍数に1足りないか、
3の倍数に2足りないかのいずれかである。
したがって、操作+を1回、または2回行うことですべての整数は3の倍数に帰着できる。
たかだか2を加えれば3の倍数になるのだから、それを3で割った数は、元の数より小さい。
したがって、操作を繰り返せば必ず3に至る。3/1で、必ず1にたどり着く。
よく似た問題ですが、おそらく未解決の問題があります。
「奇の自然数nに対して、N=3n+1(偶数)を考え、これを2で割れるだけ割った奇数の商を 先の式のnに代入する。これを繰り返すと必ず1に至る。」というものです。いくつか小さいnで試すと、数ステップで1に至るのですが、 n=27のときは、はやくも反例かという事態に遭遇します。 ところが、突然勢いが衰えて、41ステップで1になってしまいます。

(ペンネ-ム:巷の夢)
全ての正の整数は3で割れるもの、1余るもの及び2余るものに分けられる。
1~3について題意に示された計算を行うと、
1の場合 1+1= 2 → 2+1 = 3 → 3/3 = 1 即ち3回計算し、1になる。以上を念頭に置いて計算する。
2の場合 2+1 = 3 → 3/3 = 1 即ち2回計算し、1になる。
3の場合 3/3 = 1 即ち1回計算し、1になる。
(1) 24/3 = 8 → 8+1 = 9 → 9/3 = 3 この3回に上記1回を加え4回となる。
(2) 全く同様の計算を行うと、2になるまでに5回計算する。因って7回で1になる。
(3) 題意より3×3×3 =27は題意を満たす。
又、3で割ったものが2となる6も題意を満たす。
9は2回で1となるので、1を加えて9となる8も題意を満たす。
これに当初計算した1を加え、求めるものは 1、6、8及び27である。
(4) これまでの計算でも明らかだが、全ての正の整数を3で割る事を繰り返せば、必ず正の整数である1、2及び3のどれかに帰結する。即ち、どんな正数からこの計算を始めても必ず1に辿り着く。

(ペンネ-ム:暇人)
(1)①4÷3=8 ②8+1=9 ③9÷3=3 ④3÷3=1 より 4回・・・・(答)
(2)①50+1=51 ②51÷3=17 ③17+1=18 ④18÷3=6 ⑤6÷3=2 ⑥2+1=3 ⑦3÷3=1 より 7回・・・・(答)
(3)1から逆算すると
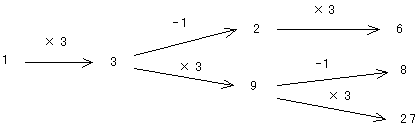
となるので, 6,8,27・・・・(答)
(4)上記操作のうち,3で割るまでの操作を1操作と考え,これを
(A)とすると上記操作は(A)の繰り返しとなる.このとき,
ⅰ)(A)によって得られる整数は1以上である.
(証明)3の倍数にした後,3で割るから明らかである.
ⅱ)2以上の整数は(A)によって元の値よりも小さくなる.
(証明)操作の対象となる整数をn,正の整数をmとすると
a)n=3mのときよってa)~c)よりⅱ)が成り立つ. ⅲ)1から始めると1に戻る.
n÷3=mより m<3m=n
b)n=3m+1のとき
n+1=3m+2⇒n+2=3m+3=3(m+1)⇒(n+2)÷3=m+1<3m+1=n
c)n=3m-1のとき
n+1=3m⇒(n+1)÷3=m<3m-1=n
(証明)1+1=2⇒2+1=3⇒3÷3=1となり,1に戻る.
以上のことから,どんな正の整数から始めても(A)の繰り返しにより1にたどり着けることがわかる.(証明終)

(ペンネ-ム:BossF)
1.整数が3で割り切れるときは、3で割ります。
2.整数が3で割り切れないときは、1を足します。
計算1を①、計算2を②とします
(1)24①8②9①3①1 4回
(2)50②51①17②18①6①2②3①1 7回
(3)最後は必ず①ですから、
①①①、①②①、②①①、②②①の4通り
すると、27、6、8、1
1は、不適ですから 6、8、27■
(4)まず、題意の演算Eは、自然数に関して閉じていることに注意します
さて、任意の自然数Nk(≠1)に対しEを行うと、高々2回の②の後①が行われます
が、その結果を Nk+1 とすると
あきらかに Nk>Nk+1ですから {Nk}は単調減少です。
したがって、任意の自然数Nは、有限回のEの後1になります■
ところで、Nが負の場合は0にたどりつきますね。
[証明]任意の整数Nk(≦-3)に対しEを行うと、高々2回の②の後①が行われますが、
その結果を Nk+1 とすると
あきらかに Nk<Nk+1<0 ですから {Nk}は単調増加です。
すなわち、任意の整数N(≦-3)は、有限回のEの後-1か、-2になります。ところ
が、-2も②により、-1になります。
さて、-1②0 ■

(ペンネ-ム:夜ふかしのつらいおじさん)
(1)[24→8→9→3→1]の4回です。
(2)[50→51→17→18→6→2→3→1]の7回です。
(3)3回の計算で最後は(1.)の決まりでなければなりません。
(2.)の決まりでは0から1増えることになるからです。
決まりが2種類しかないので次の3回の場合しか可能性がありません。
決まりが(1.1.1.)の場合、[27→9→3→1]しかし、*の場合は、はじめから1なので不適切です。
決まりが(1.2.1.)の場合、[6→2→3→1]
決まりが(2.1.1.)の場合、[8→9→3→1]
決まりが(2.2.1.)の場合、[1→2→3→1]*
(4)Ⅰ.始める自然数が1ならば、もうたどりついています。
始める自然数が2ならば、[2→3→1]
始める自然数が3ならば、[3→1]
のように、1にたどりつきます。
Ⅱ.自然数Nは、nを自然数として、
(a)3n-2、 (b)3n-1、 (c)3n
のどれかに分類できます。それぞれに決まりの計算をし、初めて3で割るところまでを1つの「まとまりの手続き」とします。するとそれぞれ次のようになります。
(a)3n-2 → 3n-1 → 3n → n
(b)3n-1 → 3n → n
(c)3n → n
N=1以外の自然数について、「まとまりの手続き」を行うと元の自然数より必ず小さな自然数となります。
(a)3n-2>n (n>1,n=1のときがN=1)
(b)3n-1>n
(c)3n>n
しかもこの自然数nを新たにNと考えると、また(a)(b)(c)のどれかに必ず分類できます。
自然数Nは有限です。「まとまりの手続き」を行うと必ず元の自然数より小さくなるので何回か「まとまりの手続き」を行えばそのうち1か2か3のどれかになるので、必ず1になってしまいます。

(ペンネ-ム:前髪)
(1) 実際にやってみます。
24→8→9→3→1 より、4回。
(2) (1)と同様に、
50→51→17→18→6→2→3→1 より、7回。
(3) 1から逆の操作をおこなってみます。
1→3→9→27
1→3→9→8
1→3→2→6
より、6,8,27の3パターンのみである。
(4) x≧1のとき、全ての自然数は
3x-2、3x-1、3x
の3パターンのどれかで書ける。これらは問いの操作により、
以上ですが、どうでしょうか。(4)の考え方としては、フェルマーの「無限降下
法」の気持ちで考えました。ペル方程式のような考え方かなとも思ったのですが。(1から任意の数
が逆操作で作れるか?)
あと、問いの計算を3進法で考えると、{}を3進法表示の数字として、
24={220}→{22}→{100}→{10}→{1}
のように、「下一桁が0なら、それを消去する。それ以外なら1を加える。」の操作と同等になり、任意の自然数の3進法表示から{1}に有限回で変形できることもいえます。

(ペンネ-ム:三角定規)
(1)
| ① | ② | ③ | ④ | |
| 24 | →8 | →9 | →3 | →1 |
(2)
| ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | |
| 50 | →51 | →17 | →18 | →6 | →2 | →3 | →1 |
(3) 逆にたどれば
③1の前はつねに3,3の前は
②-1 9を3で割った,9の前は
①-1-1 27を3で割った
①-1-2 8 に1を加えた
②-2 2に1を加えた,2の前は
①-2-1 6を3で割った
①-2-2 1に1を加えた ← これはない [答]6,8,27
(4)[証明]
与えられた初期値Nに対し 3n≦N<3n+1 を満たす整数n(n≧0)は一意的に定まる。
このとき,Nを3進数で表すとn + 1桁の数となり,各桁の数を10進数のように左から並べて
{tntn-1…t1t0}と表すことにする。ここで,tn≠0,tk (k=0,1,n-1)は0,1,2である。
以上より,操作を重ね(ⅰ)を行う度に3進数表示の桁数が減っていくから,最終的には1になる。(ⅰ) Nが3の倍数のとき,t0=0で,Nを3で割ることは3進数表示を1桁右にずらす
{tntn-1…t1t0}→{tntn-1…t1}ことを意味し,n桁の3進数になる。
(ⅱ) Nが3の倍数でないとき,t0=1,2。
(A) t0=1のとき,Nに1を加えればt0=2となり,次の(B)の場合となる。
(B) t0=2のとき
① tn,tn-1,…,t1 がすべて2ならばN=3n+1-1 で,これに1を加える
とN=3n+1,tn+1=1,tn=tn-1=…=t0=0となる。このNは,この後n+1回続けて3で割れ,1になる。
② tn,tn-1,…,t1 に0または1があれば,tn,tn-1,…,t1 のいずれかが1増えることで+1の影響を吸収できる。そして+1の後 t0=0となり,この後(ⅰ)に帰着する。
問題文をざっと一読して、「あっ、角谷の予想! あれ? 角谷の予想って証明できたん
だっけ?」Yahooで“角谷の予想”をきちんと調べて、「な~んだ、ちょっとちがうんだ」。
だけど、これができるんだから、“角谷の予想”だって同じ方法で証明できないのかな? と、しばしいじくってみましたが 、やはり簡単にはいかないようですね。

(ペンネ-ム:Toru)
(1) ?24÷3=8 ?8+1=9 ? 9÷3=3 ?3÷1=1 ということで4回
(2) ?50+1=51 ?51÷3=17 ? 17+1=18 ?18÷3=6 ?6÷3=2 ? 2+1=3 ?3
÷3=1ということで7回
(3) 逆に計算してみると3をかけるか1を引くことになります。
?1×3=3 ?3-1=2 or 3×3=9 ?2×3=6, 9-1=8, 9×3=27 ということで6,8,27
(4-1) 証明1
与えられた正の整数をN(0)とすると、連続する3つの正整数N(0),N(0)+1,N(0)+2のうちどれかは3で割り切れるので、この商をN(1)とする
とN(1)も正の整数で、
N(0)>1ならば、N(0)-N(1)≧N(0)-(N(0)+2)/3=(N(0)-1)×2/3>0よりN(0)>N(1)、
N(0)=1ならN(0)=N(1)、
同様にN(1),N(1)+1,N(1)+2のうちどれかは3で割り切れるので、この商をN(2)とするとN(2)>1ならN(1)>N(2),N(1)=1な
らN(1)=N(2)、同様に N(3),N(4),---と順に決めていくと、一般にN(k)も正の整数で、
N(k)>N(k+1) (N(k)>1),N(k)=N(k+1) (N(k)=1)となる。あらゆる与えられたN(0)に対
してN(0)より小さい正の整数は有限個しかないので十分な回数くり返せば
N(0)>N(1)>N(2)>N(3)>N(4)>------->N(m)=N(m+1)=--------=1
となるようなmが存在することが示された。
(4-2) 証明2
ある正の整数N>1を与えられた時(N=1の時は明らか)3n-1<N≦3nとなるn(n=1,2,---)が存在し、3n-N=Mとすれば、0≦M<2×3n-1より Mを3
進法であらわすとn桁以下になって、これを
A1A2A3------An (A1=0,1,Ak=0,1,2(k=2
~n))
とすると、10進法では
M=A1×3n-1+A2×3n-2+--------+An-1×3+An
となる。この時
N=3n―M=3n―A1×3n-1―A2×3n-2-----------An-1×3
-An =(---((((((1×3-A1)×3-A2)×3-A3)×3-A4)×3--------An-1)×3)-An
だから、Nに1をAk回(k=n→1)足して3で割る計算をくり返していけば最終的に1とな
る。必要な計算の回数は1を足すのがΣAk(k=1~n)回,3で割るのがn回で、n+ΣAk 回。
いつも楽しませてもらってありがとうございます。今回は3進法の問題ですね。たと
えば(2)の50は3進法では1212でやっていることは、1の位が0になるまで1をたして、
0をとるくり返しで、1212→1220→122→200→20→2→10→1の7回ということです。
(決まり2)が1を足すのでなくて、1を引くのなら、このまま単純にいけますが、足
す場合は繰り上がりがあったりするので、ちょっと工夫して証明2のようにしてみま
した。この場合は50なら1212=10000-1011とすれば、1を足す操作が3回、0をとる(3
で割る)操作が4回で計7回であることがすぐに分かります。最終的に1になるのは、
直感的には当たり前のことのようですが、きちんと証明しようとするとなかなか考え
させられました。

(ペンネ-ム:浜田 明巳)
エクセルのマクロで解きました.
(1) 4回
(2) 7回
(3) 1000000以下の正整数の中では,6,8,27の3個だけでした.
(4) 1000000以下の正整数において成り立つ(マクロが何もなく終了する)ことを示しました.
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Range("A1").Select
Dim n As Long
Dim kotae As Integer
Dim mondai As Integer
Dim max As Long
For mondai = 1 To 2
If mondai = 1 Then
n = 24
Else
n = 50
End If
Cells(mondai, 1).Value = kaisuu(n)
Next mondai
'
max = 1000000 '********
kotae = 0
For n = 1 To max
If kaisuu(n) = 3 Then
kotae = kotae + 1
Cells(3, kotae).Value = n
End If
Next n
Cells(4, 1).Value = "このマクロで,n≦" + Str(max) + "のnにおいて,すべて1になることを示しました."
End Sub
Private Function kaisuu(ByVal n As Long) As Long
Dim nn As Long
nn = n
kaisuu = 0
While nn <> 1
kaisuu = kaisuu + 1
If nn Mod 3 = 0 Then
nn = nn / 3
Else
nn = nn + 1
End If
Wend
End Function

(ペンネ-ム:kiyo)
(1)4回
(2)7回
(3)6, 8, 27
おまけ
正の整数をNとする。
高々3回の操作で元の数より小さくすることが出来る。したがって、どんな正の整数から始めても、有限回の操作で必ず1にたどりつくことが出来る。
おまけのおまけ
n回の操作で1となる正の整数の個数を、F(n)とする。
F(1)=1,F(2)=2,F(3)=3
F(n+3)=F(n+2)+F(n+1)+F(n)
トリボナッチ数列ですね。

(ペンネ-ム:kirkland)
| A君 | 「(1)、(2)はそのままですよね。24→8→9→3→1で4回と、50→51→17→18→6→2→3→1で7回です。」 | |||||||||||
| 先生 | 「(3)は、どうする?」 | |||||||||||
| A君 | 「う~ん、逆から考えていったらいいんじゃないですか。3回目に1になるには2回目は3です。0はだめですよね。2回目に3になるためには、1回目は9か2です。表にまとめた方が早いですね。というわけで6、8、27の3個」
| |||||||||||
| 先生 | 「ところで、4回の計算で1になる数は何個か分かるかな?表を書かずに考えよう。まず、すべての数は3で割るとその余りが0か1か2になるね。以下、4回の計算で1になる数全体をA4と書くことにしよう。A3、A2等も同様だ。A4に含まれる数のうち、3で割った余りが0のものは何個あるか分かるか?」 | |||||||||||
| A君 | 「これは簡単。A3の数をそれぞれ3倍したものですから、個数はA3全体の個数と同じです。」 | |||||||||||
| 先生 | 「その通り。次はA4に含まれる数のうち、3で割って2余る数は?」 | |||||||||||
| A君 | 「A3に含まれる3の倍数から1引いたものだから、A3の3の倍数の個数と等しい。ということは、A2全体の個数と同じですね。」 | |||||||||||
| 先生 | 「順調、順調。残るは、A4のうち3で割って1余る数だ。」 | |||||||||||
| A君 | 「A3のうちで3で割って2余る数の個数と等しいので、A1全体の個数と同じです。ということは、A4全体の個数は、A1、A2、A3それぞれの個数の和になって、1+2+3=6個です。 それじゃあ、A5は2+3+6=11個ですね。」 | |||||||||||
| 先生 | 「その通り。小島先生に教わったんだが、トリボナッチ数列という名前らしいよ。さて、おまけの(4) を考えよう。」 | |||||||||||
| A君 | 「1はもちろんOK、2は2→3→1でOK、3も3→1でOKです。」 | |||||||||||
| 先生 | 「すると、4~9もすべてOKだということは分かるかな?」 | |||||||||||
| A君 | 「適当に1を加えると、4と5は6に、7、8は9に帰着できます。6、9はそれぞれ3で割ると2、3 になります。2、3はすでにOKなので、4~9はOKです。」 | |||||||||||
| 先生 | 「次は?」 | |||||||||||
| A君 | 「10~27の数は適当に1を加えて3で割ると4~9になります。4~9は既にOKであるということが 分かっているので、10~27もOKです。この感じで次は、28~81、82~243、……と順々にOKになっ ていきますね。」 | |||||||||||
| 先生 | 「まあ小学生ならそんな感じでいいだろう。厳密には数学的帰納法というものを用いるんだが。」 | |||||||||||
| A君 | 「今回は、ギャグもなく真面目に終わっちゃいましたね。うー!ストレスたまるなぁ。」 |

| リナライ | figo | 巷の夢 |
| teki | kiyo | 夢夜(むよ) |
| 仮面X | 夜ふかしのつらいおじさん | Toru |
| 前髪 | BossF | wasmath |
| 杖のおじさん | 理一郎坊ちゃん | 暇人 |
| 浜田 明巳 | スチューデント | 三角定規 |
| 瑞樹 | モルモット大臣 | バレー部 |
| Y.M | kirkland | 午年のうりぼう |

問題文が不明確でご迷惑をおかけしました。
wasmathさんの(4)「1になるまで(作業を)続ける」というのはおかしいのではないでしょうか?「1でない限り作業を続け,1になれば作業をやめる」などの表現の方が適切だと思いますが,いかがでしょう。ですが、ご指摘の通りですね。混乱を招いて申し訳ありませんでした。
(4)について、結果は容易に納得できるのですが、いざ証明となるとなかなかむずかしいですね。 数学帰納法や、背理法なども用いて証明していただきました。 大局的にみれば減少数列であることと、有限であるというところを押さえていただければいいのかなと思います。
kiyoさん、kirklandさんの解答にありますように、 n回の操作で1となる正の整数の個数をF(n)とおく数列を作ると、トリボナッチ数列になります。 考えてみれば確かにそうなのですが、驚きですね。
夢夜さんの3進法表示による計算回数の考察はなかなか興味深く読ませていただきました。
類似の未解決問題をいただきましたので、ここに改めて載せさせていただきたいと思います。
理一郎坊ちゃんから、「奇の自然数nに対して、N=3n+1(偶数)を考え、これを2で割れるだけ割った奇数の商を先の式のnに代入する。これを繰り返すと必ず1に至る。」三角定規さんから、角谷の予想
「2以上の整数をどのように選んでも
(1) 偶数ならば2で割る. (2) 奇数ならば3倍して1加える.
という操作を繰り返し行うと,最後は必ず1になる」

 E-mail
E-mail
 戻る
戻る
 top
top