Weekend Mathematics/問題/問題73
73.2003年の問題
図1
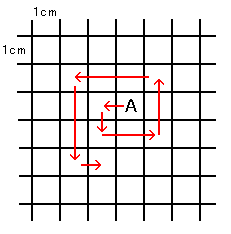
図1のような1目が1cmの方眼があります。Aから矢印のような方眼を1個ずつ塗ることにしました。
例えば、方眼を5個塗ったとき、図2にようになります。以下の問いに答えなさい。
(1)方眼を15個塗った図形の周の長さを求めなさい。
(2)方眼を15個塗った図形と周の長さが同じになるのは、方眼をいくつ塗ったときですか?
当てはまる数をすべて答えなさい。
図2
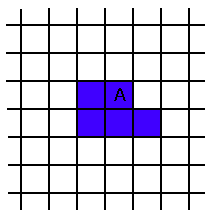
(3)方眼を2003個塗った図形の周の長さを求めなさい。
(4)方眼を2003個塗った図形と周の長さが同じになるのは、方眼をいくつ塗ったときですか?当てはまる数のうち、最も小さい数と、最も大きい数を答えなさい。
問題の出典
パズルより面白い中学入試の算数
ピーター・フランクル
講談社
お茶の水女子大学附属中学校'92入試・改題
答えと解説

答えと解説
解答・その1
(ペンネ-ム:WHORYU)
(1)15個塗ったときは、4*4=16の正方形から、1個欠けた状態です。
したがって、周長は4*4の正方形と同じ16cm。
(2)上記と同様に考えて、同じ周長は、13.14.(15).16個の場合です。
(3)2003の平方根は44.7・・・より、2003=45*44+23。
したがって周長は正方形45*45と同じ45*4=180cm
(4)正方形45*45と同じ周長の図形は、
最小45*44+1=1981
最大45*45=2025

解答・その2
(ペンネ-ム:kiyo)
(1)
15=42-1
4*4=16
答え 16cm
(2)
最大 4*4=16 4*4=16
最小 3*4+1
答え 13、14、15(今回のもの)、16
(3)
2003=452-22
45*4=180
答え 180cm
(4)
最も小さい数 44*45+1=1981
最も大きい数 45*45=2025

解答・その3
(ペンネ-ム:Banyanyan)
こういうのは、簡単な場合を調べて、規則性を発見するとうまくいくはず。(?)
とりあえず、調べてみましょう。
| 1個 | 1×4=4cm | →1×1
|
| 2個 | (1+2)×2=6cm | →1×2
|
| 3個 | 2×4=8cm |
|
| 4個 | 2×4=8cm | →2×2
|
| 5個 | (2+3)×2=10cm |
|
| 6個 | (2+3)×2=10cm | →2×3
|
| 7個 | 3×4=12cm |
|
| 8個 | 3×4=12cm |
|
| 9個 | 3×4=12cm | →3×3
|
| 10個 | (3+4)×2=14cm |
|
よって、
(N-1)×(N-1)個より多く、(N-1)×N個以下の場合
(N-1+N)×2=N×4-2cm
(N-1)×N個より多く、N×N個以下の場合
N×4cm
(1)
15個は、3×4=12個より多く、4×4=16個以下だから
16個の場合と同じだから、4×4=16cm
(2)
(1)より13個、14個、16個
(3)
2003個は、44×45=1980個より多く、45×45=2025個以下だか
ら45×4=180cm
(4)
最小 44×45+1=1981個
最大 45×45=2025個

解答・その4
(ペンネ-ム:リナライ)
まず、これは四角形の四隅から一つ出た時に周の長さが2cm伸びます。
例えば、マスが一つ塗りつぶされてる時から二つ塗りつぶされる時に周の長さが2cm増えます。
二つ目から三つ目も同じです。
三つ目から四つ目は、四隅の間になるので長さの変化はありません。
つまり、マスが塗りつぶされる時、大きい四角形が出来て、次に塗りつぶされる時は周の長さが2cm長くなります。
また、四角形は常に横-縦が1または0の長方形か正方形となります。
なので、長方形の時に次の隅まで行くための必要な長さが1大きくなります。
周の長さが2cm増えるのに必要なマス目の数を順に表わすと、1マス塗ってある所から、
1、1、2、2、3、3、4、4、5、5……と、二つ進むごとに1cm大きくなります。
この数列の和を考えることにより、
長方形または正方形になるのは
n=1、2、4、6、9、12、16、20、25、30……の場合になります。
(1)n=15の時、12<n<16の範囲にあります。
従って周の長さがn=16の時と等しくなるので
4×4=16
A 16cm
(2)12<n<16により、
13マス塗ったときから16マス塗ったときまで、周の長さは常に同じである。
(3)n=2003の時は……数字がでかすぎますね(^^;
長方形または正方形になるnの列は、n2とn(n+1)が交互に続いていて、
12、1(1+1)、22、2(2+1)……となります。
44×45=1980、452=2025より、44×45<2003<452
従って、452=2025の時と周の長さは同じ。
4×45=180
A 180cm
(4)(3)の途中経過より
44×45<2003<452
当てはまる数の最小は1981、最大は2025

解答・その5
(ペンネ-ム:高橋 道広)
答え (1)16cm (2) 13,14,(15),16個 (3) 180cm (4)小さい数1981個 大きい数2025個
(1)(2)
図の赤い線と青い線は同じ長さなので同じ辺上では正方形を1個増減しても周囲
の長さは変わらないことから 13個から16個まで塗ったときの周囲の長さはかわ
らない。よって15個の周囲の長さは16個の周囲の長さと同じで4×4=16cm
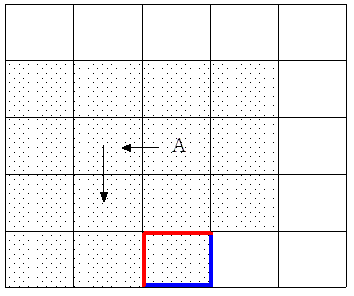
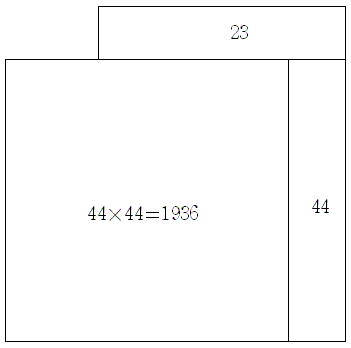
(3)(4)
一周して右下の位置に来たときには一辺が偶数の正方形状になることに気をつけ
ると44×44=1936であることから さらに正方形を塗るとひとつ飛び出て右に1
列44個塗りつぶされ、更に上辺に23個塗ると2003個塗ったことになる。
(1)と同じように、同じ辺上では周囲の長さが変わらず、角からひとつ飛び出る
と周囲の長さが2増えることから、上辺の正方形を増減しても周囲の長さは変わ
らない。
よってもっとも少なくて 2003-22=1981個 最も多くて 45×45=2025個を塗っ
たときと同じ周囲の長さになる。
また、周囲の長さは 45×45の正方形の周囲の長さと同じで 4×45=180cmとな
る。

解答・その6
(ペンネ-ム:たかまつ ろろ)
(1)答え 16cm
1目の面積が1cm2なので目の個数がそのまま面積と考えられる。
1辺が4cmの正方形(4×4=16)の角から1個引いた形になる。正方形の欠けた
部分の辺は左右に移動させてもとの正方形と重ねることができるので周囲の長さはも
との正方形と変わらない。よって、
4×4=16
(2)答え 13,14,16
1辺が4cmの正方形になる形はこれしかない。
12個だと3×4の長方形になり
17個だと4×5の長方形の仲間になってしまうから
(3)答え 180cm
2003個で1辺が何センチの正方形を作れるかを考える時そのまま√を使えば簡単
だが試験会場などには電卓は持ち込めないのでとりあえず割りやすい2000を使っ
て素因数分解を行い
| 2000 | =2×2×2×2×5×5×5
|
| =(20√5)2
|
| ≒45
|
45×45=2025
2025-2003=22
つまり1辺が45センチの正方形の1辺から22個引いた形になる。
(1)と同様にもとの正方形と周の長さは変わらないので
45×4=180
(4)答え 1981と2025
最も大きい時は
45×45=2025
の正方形の時で
最も小さい時は1辺が45cmを維持できるために1個でも角に残っている時の
2025ー44=1981
となる。

解答・その7
(ペンネ-ム:仮面X)
(1)16cm、(2)13,14,16(個)、(3)180cm、(4)1981個、2025個
周の長さは順に
④、6」⑧,8、10,10」⑫,12,12、14,14,14」⑯,16,16,16、18,18,18,18」⑳,20,20,20,20、22,22,22,22.22」・・・・・です。
(1)、(2)
(1+1)+(2+2)+(3+3)+1=13、(1+1)+(2+2)+(3+3)+4=16
なので方眼が13~16個のとき周の長さは16cmです。
(3)、(4)
(1+1)+(2+2)+(3+3)+・・・・・+(44+44)=(44+1)×44=1980
なので2003番目は44番目の」の次から数えて23番目になります。
44番目の」の次は4×45=180です。それで、1981番目~2025番目まで180が
45個ならびます。

解答・その8
(ペンネ-ム:午年のうりぼう)
(1)、(2) 実際に図を描いて、周の長さを測ってみると、
| 色を塗られた方眼の個数(個)
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
| 16
| 17
|
|---|
| 色を塗られた方眼の周の長さ(㎝)
| 4
| 6
| 8
| 8
| 10
| 10
| 12
| 12
| 12
| 14
| 14
| 14
| 16
| 16
| 16
| 16
| 18
|
|---|
∴ (1) 16 (2) 13,14,(15),16 …(答)
(3) まず、色を塗られた部分がAを中心とした正方形になるときを基準にして考える。
色を塗られた部分がAを中心とした正方形になるのは、色を塗られた方眼の個数が
(2n-1)2(n=1,2,3,……)個のときだから、まず、
(2n-1)2≦ 2003 となる最大のnを求めると、
| (2n-1)2 ≦ 2003
|
| ⇔ | 2n2-2n-1001≦0
|
| ⇔ | (1-√2003)/2 ≦ n ≦(1+√2003)/2
|
よって、もとめるnは、44<√2003<45 より、n=22
つまり、2003は、432=1849<2003<452=2025 にある。状況は次図の通り。
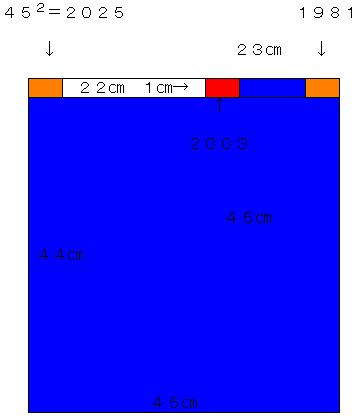
上図より、求める周の長さは
44+45+45+23+1+22=180(㎝)…(答)
(4) 色を塗られた部分が上図のようなとき、長方形または正方形になるまで方眼を1つ塗ると、元の図形の周の長さをx(㎝)とすると、周の長さは x+2-2=x(㎝) のままであり、色を塗られた部分が長方形または正方形のとき、方眼を1つ塗ると、周の長さは
x+3-1=x+2(㎝) となる(下図)。
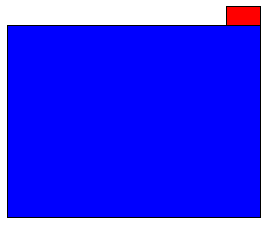
よって、方眼を2003個塗った図形と周の長さが同じになるのは、方眼を
1981個塗ったときから2025個塗ったときまでである。
∴ 最も小さい数:1981 , 最も大きい数:2025 …(答)

解答・その9
(ペンネ-ム:kirkland)
| A君 | 「早速ですが、15個ぐらいだったら描いた方が早いんじゃないですか?」
|
| 先生 | 「まぁ、そういうことだ。あとは、一人で考えなさい。」
|
| A君 | 「図形描画ツールと、表を挿入するのと、どっちが楽ですかね?」
|
| 先生 | 「まぁ、似たようなもんじゃないの?好きにしなさい。」
|
| A君 | 「図形描画だと、少しずれてしまいましたね。数えると、(1)は、16cmですね。」
|
| 先生 | 「どうやって数えたの?」
|
| A君 | 「先生、僕を馬鹿にしてます?16ぐらいまでの数は知ってますよ!」
|
| 先生 | 「いやぁ、そのまま数えると、(3)なんて無理だろうよ。」
|
| A君 | 「はははっ、そんなもんは気合いで解決ですよ!」
|
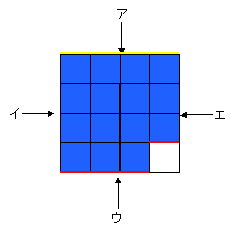
| 先生 | 「面倒なことは好かん。ヒントをあげよう。ア~エの矢印の方向からそれぞれ見てごらん。あとは、一人で考えなさい。」
|
| A君 | 「アの方から見て、見える長さは4cm(黄線)。イも同様。ウの方から見ても4cmですね(赤線)。エも同様。」
|
| 先生 | 「まぁ、そういうことだ。あとは、一人で考えなさい。」
|
| A君 | 「角が欠けていても、結局4×4の正方形の周りの長さと同じなんですね。ということは、(2)は、13~16個ですね。
12個にしてしまうと、出っ張っている部分がなくなって長方形になってしまいますもんね。」
|
| 先生 | 「まぁ、そういうことだ。あとは、一人で考えなさい。」
|
| A君 | 「(3)で、2003個のときの図形より少し大きな正方形を考えると、45×45(=2025)の正方形です。2003個のときの図
形の周りの長さは、この正方形の周の長さと同じだから45×4=180cmですね。」
|
| 先生 | 「まぁ、そういうことだ。あとは、一人で考えなさい。」
|
| A君 | 「出っ張っている部分がなくなって長方形になっちゃダメで、45×44=1980個の図形はダメなんだから、
(4)は最小が1981個で、最大が2025個ということになりますね。」
|
| 先生 | 「まぁ、そういうことだ。」
|
| A君 | 「先生、今日は何か、サボってません?」
|
| 先生 | 「二日酔いで頭が痛いんだよ。」
|
| A君 | 「職務怠慢ですね。減給するよう、校長先生に直訴してきま~す!」
|

解答・その10
(ペンネ-ム:マセがき)
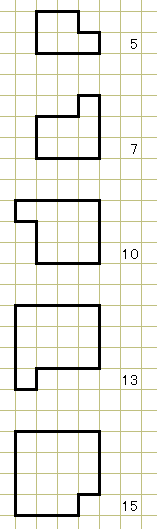
図形の周の長さが変化するのは、元の図形が正方形か長方形だったときに、ひとつだけ飛び出した形となるときのみで、この場合周の長さが3cm増えて、1cm減るため、差し引き2cm増加します。その他の場合は、周の長さが2cm増えて、2cm減ることとなるため、差し引き、増減は無い状態となります。
ここで、図形が正方形となるのは、nを自然数として、方眼のマスの数がn2となるときなので、1・4・9・16・25・・・・個塗ったときになります。また、長方形となる場合は、n2+n個を塗ったときとなるので、2・6・12・20・30・・・個塗ったときになります。
よって、周の長さが変化するのは、n2+1個とn2+n+1個塗ったときのみとなります。
では、x個のマスを塗ったときの周の長さを求めてみましょう。まず、xの正の平方根より小さい最大の整数を求めて、これをaとおきます。このaが今の形に塗る直前の最も大きい正方形の一辺の長さになります。次に、aが求められたら、a2+aとxを比較します。ここで、xがこの値より大きい場合は、直前で最大であった正方形の次にできる長方形も、既に塗り終えていることになります。
よって、x個のマスを塗ったときにできる図形の周の長さは、x>a2+aのときは、4a+4となり、x≦a2+aのときは、4a+2となります。
最後にx個のマスを塗ったときと周の長さが同じになる範囲を求めてみましょう。x>a2+aのときは、既に長方形は塗り終えているので、このまま塗り進めていくと、一辺の長さが(a+1)の正方形ができ、そこまで塗ったとき、すなわち、(a+1)2個が周の長さが同じになる最大値となります。また、最小値は最後に塗り終えた長方形を塗った次に、一つ飛び出したところとなるため、a2+a+1個となります。x≦a2+aのときは、長方形と正方形が逆になるため、最大値はa2+a個となり、最小値がa2+1個となります。
解答
15個塗った図形の周の長さ 16cm
15個塗った図形の周の長さと同じになる個数 13個、14個、16個
2003個塗った図形の周の長さ 180cm
2003個塗った図形の周の長さと同じになる最小の個数 1981個
2003個塗った図形の周の長さと同じになる最大の個数 2025個
| 塗った数 | aの値 | 周の長さ | 最小値 | 最大値
|
|---|
| 2003 | 44 | 180 | 1981 | 2025
|

解答・その11
(ペンネ-ム:三角定規)
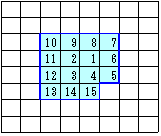
(1) 方眼を15個塗った図形は右図の水色の部分である。
その周(青線部)の長さは, 16 ……… [答]
(2) 周長が16になるのは,塗った数が 13,14,(15),16 …[答]
(3)(4) 図より方眼を塗った数N (N≧2)が
(ⅰ)n2+1≦N≦n(n+1) のとき周長は 2(2n+1)
(ⅱ)n(n+1)+1≦N≦ (n+1)2 のとき周長は 4(n+1) (n=1,2,… )
でそれぞれ一定になっている。
(ⅱ)で n=44のとき 44(44+1)+1=1981≦2003≦2025=452 だから
方眼を2003個塗ったときの周の長さ 4・45=180
周の長さが180で等しくなるのは, 1981≦N≦2025 …[答]

解答・その12
(ペンネ-ム:理一郎坊ちゃん)
一辺がkの正方形をKと呼び、一辺が一の正方形をMと呼ぶ。Kの周囲は4*k、Mの周囲は4。
KにMを1個加えると、4辺が加わることになるが、KとMの1辺ずつが重なり図形の中に含まれてしまうので、4-2=2辺増える。k2+2個目からk2+k個目までは、Mを1個加えるとKと直前のMの1辺ずつが重なり図形の中に含まれてしまうので、
4-2-2=0となり、辺の数は増えない。これらの現象が繰り代えされることになる。
KにMが1個からk個加わるとき、周囲は4*k+2。ここまででこの図形は、一辺が、kとk+1の長方形になる。
k2+k+1個目のMを加えると、周囲は2増えて4k+4。以後Mを(k+1)2個になるまで加えても、周囲は4*k+4。
(1)16cm。k=3とすると、32<32+3<15<16より。
(2)13,14,(15),16個。32+3+1から(3+1)2まで。
(3)180cm。442=1936、442+44+1=1981<2003<452=2025より、一辺45の正方形と等しい。
(4)1981,2025。(3)と同様。

解答・その13
(ペンネ-ム:夜ふかしのつらいおじさん)
以下のように色を塗る順番に自然数をつけていきます。
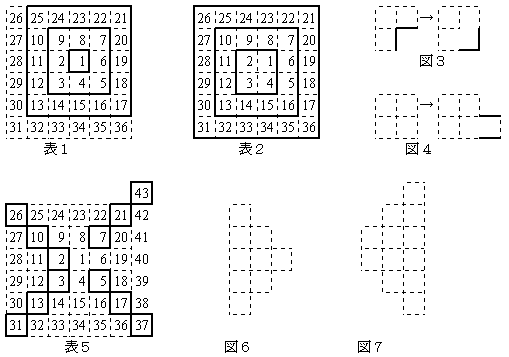
表1のように「1」を中心に上下左右に1つずつ正方形を大きくしていきます。すると正方形の左上は{1,9,25,49,・・・}のように奇数の平方数です。
表2のように「1234」を中心に上下左右に1つずつ正方形を大きくしていきます。すると正方形の右下は{4,16,36,64、・・・}のように偶数の平方数です。
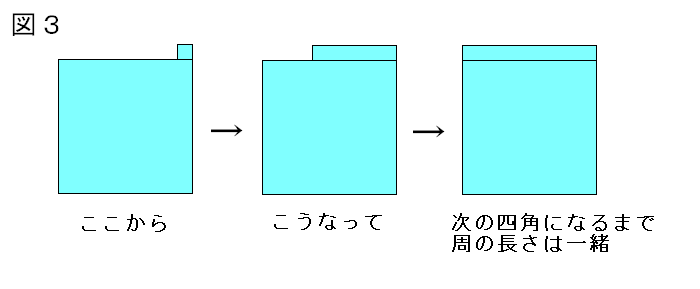
さて、図3のように凹型6角形の状態で数を増やすとき面積は1平方センチメートル増えますが周の長さは変わりません。図4のように長方形の状態で数を増やすとき周の長さは2センチメートル増えます。
つまり表5の太線で囲まれた数が長方形から飛び出す数で周の長さを2増やします。
左上に増える数{2,10,26,・・・}は、奇数の平方数に1を加えた数です。
左下に増える数{3,13,31,・・・}は、上の数に図6のように奇数を加えた数です。
右下に増える数{5,17,37,・・・}は、偶数の平方数に1を加えた数です。
右上に増える数{7,21,43,・・・}は、上の数に図7のように偶数を加えた数です。まとめると、
| 左上の数は(2n-1)2+1 | =4n2-4n+2
|
| 左下の数は(2n-1)2+1+(2n-1) | =4n2-2n+1
|
| 右下の数は(2n )2+1 | =4n2 +1
|
| 右上の数は(2n )2+1+(2n) | =4n2+2n+1
|
となります。
(1)方眼を15個塗ったときの周の長さは、16個のときと同じです。
16個のときは、1辺が4センチメートルの正方形です。
だから求める周の長さは、4×4=16センチメートルです。
(2)13,14,(15),16個のときが同じ長さです。
(3)上の式で2003に近いものを探します。このとき見当をつけるには、
3番目の式 4n2+1=2003 をおおざっぱに n2=500
とすると良いと思います。
| n | 22 | 23
|
|---|
| 左上 4n2-4n+2 | 1850 | 2026
|
| 左下 4n2-2n+1 | 1893 | 2071
|
| 右下 4n2 +1 | 1937 | 2117
|
| 右上 4n2+2n+1 | 1981 | 2163
|
この表より次のようになっていることが分かります。
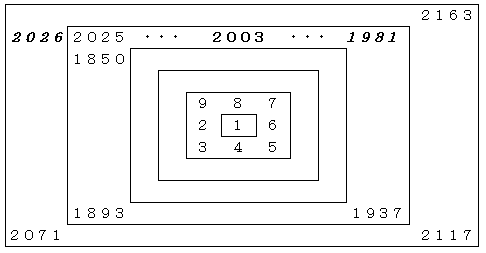
方眼を2003個塗ったときの周の長さは、2025個のときと同じです。
2025個のときは、1辺が45センチメートルの正方形です。
だから求める周の長さは、4×45=180センチメートルです。
(4)1981と2025です。

解答・その14
(ペンネ-ム:巷の夢)
(1) 方眼15個を塗った図形の周の長さは16個塗った正方形と同じだから16cm
(2) 正方形や長方形から一つ飛び出す毎に周の長さが変わるので、(1)を考慮すると、15個塗ったのと同じ周長となるのは13,14,16個塗った時である。
(3) 順次塗る方眼の数を増やしていくと、以下の様になる。
| 方眼数 | 周長 | 方眼数 | 周長 | 方眼数 | 周長 | 方眼数 | 周長 | 方眼数 | 周長
|
|---|
| 1 | 4 | 3 | 8
| 7 | 12 | 13 | 16
| 21 | 20
|
| 2 | 6 | 4 | 8
| 8 | 12 | 14 | 16
| 22 | 20
|
| | | 5 | 10 | 9 | 12
| 15 | 16 | 23 | 20
|
| | | 6 | 10 | 10 | 14
| 16 | 16 | 24 | 20
|
| | | | | 11 | 14 | 17
| 18 | 25 | 20
|
| | | | | 12 | 14 | 18
| 18 | 26 | 22
|
| | | | | | | 19 | 18 | 27
| 22
|
| | | | | | | 20 | 18 | 28
| 22
|
| | | | | | | | | 29 | 22
|
| | | | | | | | | 30 | 22
|
これより各列の方眼数の増加と共に周長の同じ物が2,3,4,5と増えていくことが分かる。因って各列の周長を平均で以下の様に表す。
| 方眼数の差 | 平均周長
|
|---|
| 2 | 5
|
| 4(上の表の6と2の差) | 9
|
| 6(上の表の12と6の差) | 13
|
| 8(上の表の20と12の差) | 17
|
| |
|
| 2N | 4N+1
|
これより、方眼数の差を加えていけば最終的に塗られた方眼数となるから、2003は
Σ2N=N(N+1)より、N=44と45の間にあることが分かる。又、N=44で塗られた方眼の最大数は1980であるから2003はN=45に属することが分かる。因って平均周長は4N+1であるから181となる。この値は180と182の平均である。以上より2003個塗った方眼の周長は180cmである。
(4)(3)より周長180cmの塗られた方眼数の最初は1981、最後は45番目であるから44を加え2025となる。これらは最も小さい数と最も大きい数に対応しているので、これらが求めるものである。

解答・その15
(ペンネ-ム:水の流れ)
最初は規則性を見るために 順に数えていきます。
1cmの方眼の個数をk(自然数)個とし、図形の周をLcmとする。
(1)長方形が完成されたとき、横の長さをncmとすると、縦は(n-1)cmとなる。
(2)正方形が完成されたとき、2辺の長さをncmとする。
| k=1のとき、 | L=4
|
| k=2のとき、 | L=6
|
| k=3のとき、 | L=8
|
| k=4のとき、 | L=8
|
| k=5のとき、 | L=10
|
| k=6のとき、 | L=10
|
| k=7のとき、 | L=12
|
| k=8のとき、 | L=12
|
| k=9のとき、 | L=12
|
| k=10のとき、 | L=14
|
| k=11のとき、 | L=14
|
| k=12のとき、 | L=14
|
| k=13のとき、 | L=16
|
| k=14のとき、 | L=16
|
| k=15のとき、 | L=16
|
| k=16のとき、 | L=16
|
| k=17のとき、 | L=18
|
| ・・・・・・ |
|
ここで、一般に
(1)k=n×(n-1)のとき、
2辺の長さが横ncm、縦(n-1)cmの長方形を表し、周の長さL=(4n-2)cm
(2)k=n×nのとき、
2辺の長さをncmの正方形で、周の長さがL=4n cm
したがって、これをkで分類すると、(1≦nの自然数)
(1)(n-1)・(n-1)<k≦n(n-1) のとき、L=4n-2
(2)n(n-1)<k≦n・nのとき、 L=4n
以上から、
問題1は 4×3<k=15≦4×4 より L=4・4=16cm
問題2は、L=16=4・4から、4×3<k=15≦4×4だから
よって、k=13,14,15,16
問題3は、2003前後の平方数を見つけると 44・44=1936
45・44=1980
45・45=2025
よって、44×45<k=2003≦45×45 から L=4・45=180 cm
問題4は、44×45<k=2003≦45×45 から
kの最小値は1981(個) 、 kの最大値は2025(個) 終わり

解答・その16
(ペンネ-ム:柿本 浩)
まぁ、まずはロジックを考えてみましょ。
それが分かれば15も2003も同じです。
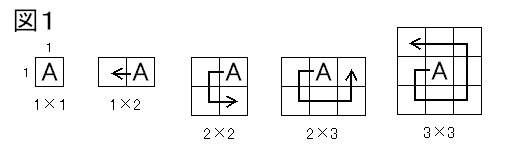
まず、図1の様に考えてゆくと、問題の手順で方眼を塗りつぶしてゆく途中で
●n×nの正方形
●n×(n+1)の長方形
※nは全ての自然数
を形づくるパターンがある事が分かる。 ・・・ 共通解
次に、塗りつぶす方眼が1マス増えた時の周の長さの変化を考えると
図2の様に『塗りつぶすマスの上下左右4箇所のマスが既に塗りつぶされているかど
うか』によって変わってくる事が分かる。
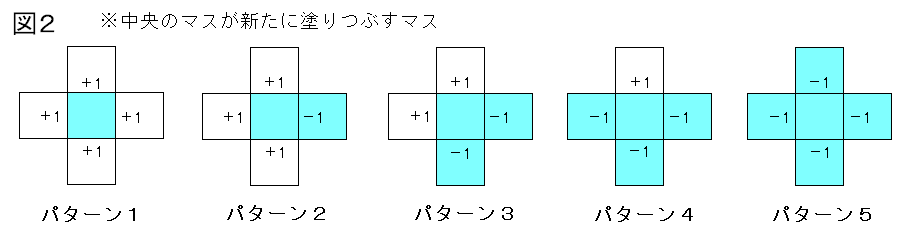
●パターン1:4箇所とも空の場合(+4cm)
→ 最初のマス(A)を塗りつぶす時のみ、それ以降は隣接するマスを塗っていく
ため有り得ない。
●パターン2:3箇所空の場合(+2cm)
→ 問題文のケースでは、四角形(共通解1の正方形・長方形)が出来た次の1マ
スがこれに当たる。
●パターン3:2箇所空の場合(±0cm)
→ 問題文のケースでは、パターン1・2以外は全てこれに当たる。
●パターン4:1箇所空の場合(-2cm)
→ 問題文のケースでは有り得ないパターン。
●パターン5:4箇所とも塗られていた場合(-4cm)
→ 問題文のケースでは有り得ないパターン。
これより問題の図形の外周の長さは
最初の1個は+4cm(0→4cm)で、それ以降は
四角形(共通解1の正方形・長方形)が出来た次の1個を塗る時のみ
+2cmとなり、それ以外のパターンでは変わらない事が分かる。
つまり、マス目を塗りつぶして四角形以外の形になった場合は
そのまま塗り進めて次に出来る四角形と外周の長さが同じになる。 ・・・ 共通解
2
(図3参照)
これより
(1)
面積は当然15cm2の図形であり、これは
12個目:3×4=12cm2の長方形と
16個目:4×4=16cm2の正方形の間に出来る形である。
よって共通解2より、この図形の外周の長さは4×4の正方形と同じである事が分かり
周の長さは4(cm)×4(辺)=16cmとなる。
(2)
(1)の解と共通解2より、13個目(12個目の長方形+1)から
16個目の正方形までは外周の長さが同じである事が分かる。
これより、15個の図形と周の長さが一致するのは、13、14、16個を塗りつぶ
した時である。
(3)
面積は当然2003cm2の図形であり、これは
1980個目:44×45=1980cm2の長方形と
2025個目:45×45=2025cm2の正方形の間に出来る形である。
よって共通解2より、この図形の外周の長さは45×45の正方形と同じである事が
分かり周の長さは、45(cm)×4(辺)=180cmとなる。
(4)
(3)の解と、共通解2より、1981個目(1980個目の長方形+1)から
2025個目の正方形までは外周の長さが同じである事が分かる。
よって2003個の形と外周の長さが同じになる最も小さい数は1981個で
最も大きい数は2025個を塗りつぶした時である。

解答・その17
(ペンネ-ム:モルモット大臣)
規則性から塗られた方眼の全体個数NがK2(K≧2)個の時、その外周は4K cmである。
(K+1)2-K2=2K+1であり、その個数NがK2+1≦N≦K2+Kの場合、その外周は4K+2 cm
その個数がK2+K+1≦N≦(K+1)2の時は4(K+1)=4K+4 cmである。
以上から
(1) N=15の時は32<15<42であるから32+3+1=13<15<16より、前述の式でK2+K+1≦N≦(K+1)2の時は4(K+1)=4K+4 cmにおいてK=3の時、よってその外周は4×3+4=16 cm
(2) 外周が20 cmの場合の全体個数Nは(1)より32+3+1≦N≦42だから該当するNはN=13,14,15,16 よって求める答は13,14,16
(3) N=2003の時は442=1936<2003<452=2025であり、1936+44=1980<2003から前述の式、K2+K+1≦N≦(K+1)2の時は4(K+1)=4K+4 cmでK=44の時、よってその外周は4×45=180 cm
(4) 外周が180 cmの場合の全体個数Nは(3)よりK2+K+1≦N≦(K+1)2におけるK=44の時である。該当するNは442+44+1≦N≦452から1981≦N≦2025
よって外周180 cmとなるNの最小と最大の数はそれぞれ1981, 2025である。

解答・その18
(ペンネ-ム:杖のおじさん)
この問題を解くため、公式を次の様に作ります。方眼は1cm角なので図形1個の面積は1cm2となります。
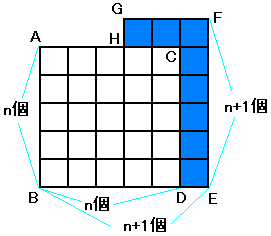 図形の面積をSとすると次の式が成り立ちます。
図形の面積をSとすると次の式が成り立ちます。
nを求める。n=√S の整数部となる。
Excelで計算する場合、
n=INT(SQRT(S))
でも、入学試験なので試験場にはパソコンを持ち込めませんので暗算ですね。
n2は正方形の面積で、Sの面積から引くと周囲の方眼の数が出ます。
周囲の方眼の面積(CDEFGH)をyとすると、
y=s-n2
(A)y-n>0の時は、
周囲の長さは、4(n+1)
周囲の長さが同じになる個数は、最小 n(n+1)+1、最大(n+1)2となります。
(B)y-n<=0の時は、
周囲の長さは、2(2n+1)
周囲の長さが同じになる個数は、最小 n2+1、最大n(n+1)となります。
上記により、(1)(2)(3)(4)を計算します。
(1)√15=3.872・・ n=3
y=15-9=6、6-3=3なので(A)より 4(3+1)=16cm
(2)(A)により、13,14,(15),16個塗ったとき同じ周囲の長さとなります。
(3)√2003=44.7548・・ n=44
y=2003-1936-67、67-44=23なので (A)より 4(44+1)=180cm
(4)(A)により、最小は 44×45+1=1981個、最大は 45×45=2025個

解答・その19
(ペンネ-ム:小学名探偵)
(1)16cm (2)13、14、16 (3)180 (4)最大2025 最小1981
単位正方形(一辺の長さ1cmの正方形)の数をXとします。
一辺の長さ2の正方形となるまで(1<X<=4)、周の長さは 2,2,0
一辺の長さ3の正方形になるまで(4<X<=9)、周の長さは 2,0,2,0、0
一辺の長さ4の正方形になるまで(9<X<=16)、周の長さは 2,0,0,2,0,0,0
と増えます。同様にして
一辺の長さn+1の正方形になるまで(n2<x<=(n+1)2)、
周の長さは、前のn個が(Xの範囲[n2+1,n2+n]のとき)+2で、4*n+2となり、
後のn+1個が(Xの範囲[n2+n+1,(n+1)2]のとき)更に+2で、4*(n+1)となる。
(1) X=15は[13,16]の範囲にあるので、周の長さ4*4=16cmです。
(2) 上より、13,14,(15)、16です。
(3) 2003は、[442+45,452]の範囲にあるので、周の長さ4*45=180になりました。
(4) 442+45=1981,452=2025

解答・その20
(ペンネ-ム:Toru)
一辺がk cm(k=1,2,3-----)の正方形、すなわちk2個塗ったところから考える。
この時、周の長さは4k cm、ここから1個塗ると、周の長さは2cm 増えて4k+2 cm、その
後k個(全体でk2+k=k(k+1)個:k、k+1の長方形)までは、周の長さは変わらず、
つぎの1個でまた2 cm増えて4k+4=4(k+1) cmとなり、これは1辺が(k+1)cmの正方
形((k+1)2個)になるまで続く。以下、同じくり返し。
よって
(1)3×3<3×4<15<4×4 より、k=3のところで考えて4×(3+1)=16
(2)3×4+1から4×4までで 13,14,(15),16
(3) 44×44<44×45<2003<45×45 (44×45=1980, 45×45=2025)よりk=44の場合
を考えて、4×(44+1)=180
(4)44×45+1から45×45までで 最小は44×45+1=1981,最大は45×45=2025

解答・その21
(ペンネ-ム:teki)
1 16cm
2 13、14、(15)、16
3 180cm
4 最小:1981 最大:2025
面白い規則性がありますね。
塗る個数をNとすると、周の長さLとの間には以下の関係があります。
(n-1)2<N≦n2-n のとき、L=4×n-2・・・①
n2-n<N≦n2 のとき、L=4×n・・・②
1は、N=15(n=4)の時で、②式が適用され、L=16となります。
2は、n=4のとき、n2-n=12 となるので、該当する数は13~16
です。
3は、442=1936、452=2025、452-45=1980 より、Lは45×4=180 となります。
4は、3でも述べたとおり、1981~2025まではL=180ですので、
最小は1981、最大は2025 となります。

解答・その22
(ペンネ-ム:浜田 明巳)
エクセルのマクロで解きました。グラフィック画面もどきになっています。
(1) 16
(2) 13,14,16
(3) 180
(4) 1981,2025
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Cells.Select
Selection.Interior.ColorIndex = xlNone
Selection.ClearContents
'
Dim x As Integer
Dim y As Integer
Dim muki As Integer
Dim n As Integer
Dim kosuu As Integer
Dim max4 As Integer
Dim min4 As Integer
Dim j As Integer
Sheets("Sheet2").Cells(1, 1).Value = 0
For n = 0 To 100
If n = 0 Then
kosuu = 1
x = 50
y = 50
Call choice(kosuu, x, y)
Else
If n = 1 Then
muki = 2
Else
muki = (muki + 1) Mod 4
End If
For j = 1 To Int((n + 1) * 0.5)
kosuu = kosuu + 1
Select Case muki
Case 0
y = y + 1
Case 1
x = x - 1
Case 2
y = y - 1
Case Else
x = x + 1
End Select
Call choice(kosuu, x, y)
Next j
End If
Next n
'
Sheets("Sheet2").Select
Cells(1, 5).Value = Cells(15, 3).Value
Range("E1").Select
'
n = 0
For j = 1 To kosuu
If j <> 15 And Cells(j, 3).Value = Cells(1, 5).Value Then
n = n + 1
Cells(2, 5 + (n - 1)).Value = Cells(j, 2).Value
End If
Next j
Range("E2").Select
Cells(3, 5).Value = Cells(2003, 3).Value
Range("E3").Select
'
min4 = kosuu
max4 = 0
For j = 1 To kosuu
If j <> 2003 And Cells(j, 3).Value = Cells(3, 5).Value Then
If min4 > Cells(j, 2).Value Then
min4 = Cells(j, 2).Value
End If
If max4 < Cells(j, 2).Value Then
max4 = Cells(j, 2).Value
End If
End If
Next j
Cells(4, 5).Value = min4
Cells(4, 6).Value = max4
Range("E4").Select
'
Range("E1").Select
End Sub
Sub choice(ByVal kosuu As Integer, ByVal x As Integer, ByVal y As Integer)
Range(Cells(x, y).Address(False, False)).Select
With Selection.Interior
.ColorIndex = 5
.Pattern = xlSolid
End With
Cells(x, y).Value = 1
Sheets("Sheet2").Cells(1, 1).Value = Sheets("Sheet2").Cells(1, 1).Value + waku(x, y)
Sheets("Sheet2").Cells(kosuu, 2).Value = kosuu
Sheets("Sheet2").Cells(kosuu, 3).Value = Sheets("Sheet2").Cells(1, 1).Value
End Sub
Private Function waku(ByVal x As Integer, ByVal y As Integer) As Integer
Dim mawari As Integer
Dim j1 As Integer
Dim j2 As Integer
mawari = 0
mawari = mawari + Cells(x, y + 1).Value
mawari = mawari + Cells(x - 1, y).Value
mawari = mawari + Cells(x, y - 1).Value
mawari = mawari + Cells(x + 1, y).Value
Select Case mawari
Case 0
waku = 4
Case 1
waku = 2
Case 2
waku = 0
Case 3
waku = -2
Case Else
waku = -4
End Select
End Function

正解者

まとめ
たくさんの解答をどうもありがとうございました。図を添えてくださる方も多く、感謝いたします。
こういった問題は、Banyanyanさんのおっしゃる通り、簡単なところで実際にやってみて規則性を探すといいですよね。この問題の規則性はなかなかおもしろいと思います。正方形n2だけではなく、長方形n(n+1)で状況が変わります。この状況を数学的に表現するために皆さんいろいろ工夫されていらっしゃいます。いつもながら、皆さんの解答を拝見して大変勉強になります。ありがとうございます。

 E-mail
E-mail
 戻る
戻る
 top
top













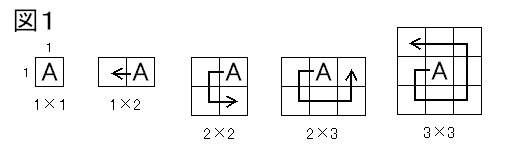


 図形の面積をSとすると次の式が成り立ちます。
図形の面積をSとすると次の式が成り立ちます。 E-mail
E-mail
 戻る
戻る
 top
top