Weekend Mathematics/問題/問題72
72.ネコとイヌの競争
よく仕込まれたネコとイヌが100フィートの直線コースを往復競争する。 イヌは1とびで3フィート、ネコは2フィート進むが、イヌが2とびするあいだにネコは 3とびする。このような条件のもとで、レースの結果はどのようなことになるか?
サム・ロイドのパズル百科
マーチン・ガードナー編 田中勇訳
白揚社
(ペンネ−ム:エルトシャン)
犬が33とびして99フィート進むと、猫は49.5とびし99フィート進む。犬は次とぶと2フィート飛び出てしまう。また、猫は犬が34とびするとき51とびすることになる。しかし、猫は50とびするときに往復地点につき、51とび目はゴールに向かってとぶことになる。よって、34とび終了時、犬はゴールまで102フィート、猫はゴールまで98フィートということになる。犬と猫のスピードは同じなので、ゴールまでの残りの距離が少ない猫の勝ちである。

(ペンネ−ム:AK)
イヌとネコは6フィートづつ一緒に進む。
ですが100フィートの折り返し地点で
イヌは行き過ぎて102フィートに行ってしまうので
折り返し直後イヌは102フィート地点、ネコは98フィート地点にいる。
ラストのゴール地点手前では
イヌが6フィート地点、ネコが2フィート地点。
よってネコが勝ってしまう。

(ペンネ−ム:三角定規)
(答)ネコが勝つ。
(理由)
スタートから96フィート地点(ネコ48とび、イヌ32とび)
までは全く互角。
この後、イヌは2とびで折り返し地点を越え102フィート
地点まで行ってしまう。ネコは、この間3とびでき、2とびで
折り返し地点に到達、もう1とびで98フィート地点に戻れる
。
すなわち、ここで4フィートの差ができ、この差はその後挽
回できない。
(感想)このように、素直に考えていいのですよね?!

(ペンネ−ム:理一郎ぼちゃん)
イヌとネコの速さは同じです。しかし、ネコは2フィートずつ進めば、丁度50回で折り返すことができますが、イヌは99フィートから
もう一飛びして、102フィートまで進まなくてはならず、往復で204フィート進む必要があります。一飛び3フィートならば、
1フィートまたは2フィート飛ぶことができるとしても、もちろん結果は同じで、ネコの勝ちです。

(ペンネ−ム:Banyanyan)
| イヌ | : | ネコ | |
| 歩幅の比 | 3 | : | 2 |
| 歩数の比 | 2 | : | 3 |
| 速さの比 | 1 | : | 1 |
ネコは
100÷2=50とび
往復でかかる時間は
<6>×50×2÷3=<200>
よって、ネコの方が早くゴールする。

(ペンネ−ム:天才小学生Mappy)
初めまして。ローマで暮らしている天才小学生Mappyです。いつも楽しくこのページ読ませてもらっています。小学校の算数の授業でこの問題を解きました。
犬が2とびすると3×2で6フィート進み、犬が2とびしている間に、猫は3とびするので2×3で6フィート進む。このように犬と猫の速さは同じになる。しかーし、犬は折り返し地点に達するとき、3×34で102フィートまで進んでしまう。それに対して猫は2×50でぴったし100フィートのところで折り返すことができる。しかも犬が34回とんだとき、猫は51かいとび、もうすでに、猫は折り返して2フィート進んでいる。この時、犬と猫の間に4フィートの差が生まれている。このまま、二匹が同じスピードで進んでいくと猫が先にゴールする。と言うことでこのレースは猫が勝つ。

(ペンネ−ム:夜ふかしのつらいおじさん)
ネコは50とびすると100フィートに達します。Uターンして100フィー
ト戻ってきます。つまり往復で200フィート走ることになります。
一方イヌは33とびすると99フィートに達します。34とび目の1/3の空
中に浮いているときに100フィートに達しますが着地したときは2フィート先
の102フィートのところまで行ってしまいます。Uターンした時点でネコは4
フィート前にいます。
イヌとネコの速さが変わらないのでネコがゴールしたときイヌはあと4フィー
トのところにいます。結局ネコの勝ちです。

(ペンネ−ム:暇人)
イヌ、ネコ共に速さは同じなので一見勝負は引き分けかと思われますが・・・。
ひととびでネコは2フィート、イヌは3フィートですから、丁度100フィートの折り返し地点では、犬は丁度ジャンプ状態にあり、速度の変更ができません。ネコは丁度着地できますので速度の変更が出来ます(∵100は2で割り切れるが、3では割り切れない)。イヌの着地地点はスタート地点から102フィートのところになり、そこから折り返すことになりますので、イヌは往復204フィート走らねばなりません。したがって速さが同じなので丁度200フィートを走ることになるネコの勝ちということになります。

(ペンネ−ム:巷の夢)
題意より犬も猫も同じ時間に進む距離は変わらない。要するに、1跳躍単位に6フィートづつ進む。因って16跳躍単位では共に96フィートまで進む。問題はここからで、猫は更に1跳躍単位で100フィートを折り返し、ゴールに向かい2フィート進む。
これに対し犬は102フィートまで進んでしまう。
因って、ゴールから102フィート離れた位置にいる犬と、同様に98フィート離れた位置にいる猫の勝負を考えれば良い。
16跳躍単位では共に96フィートまで進むので、猫はゴール2フィート前まで来る。これに対し犬はゴール6フィート前までしか来れない。
これより明らかに、この勝負は猫が勝つ。

(ペンネ−ム:リナライ)
まず、犬が3フィートを2飛び、合計6フィート進む間に猫も2フィート3飛びで、
6フィート進みますね?
この時100÷6=16 余り4
犬も猫もお互いにこの問題の鍵は最後のところになります。
先ほどの計算の余りが4ですので、96フィート地点までは同時に着きます。
この地点より、犬も猫も次の1飛びが同時の時、犬は99フィート、猫は98フィートですが、次の1飛びは犬が2飛びする間に猫は3飛びするわけですから、当然猫の方が早く飛びます。
猫が次の1飛びを先にして丁度100フィート、犬は次の瞬間に飛んで102フィート飛び、おり返し地点を越えてしまいます。
もちろん、その間に猫は2フィート飛んでいますので、98フィート地点に戻ります。
ここから再び同時に1飛びから始まりますが、犬は102フィート、猫は98フィートで4フィートの差が出るので、犬も猫も、最初に書いた通り同時に6フィートずつ進むので、当然猫の勝ちです。

(ペンネ−ム:高橋 道広)
答え ネコの勝ちっ
さて今月の問題の解答です。
イヌが2飛びして6フィート進む間にネコは3飛びして6フィート進む。
なあんだ同じ速さじゃないか 答えは 同着っ。
いやまてよ 何度こんなことで煮え湯を飲まされたかわからない。
100フィート3フィートということは...イヌは行き過ぎじゃん。
のこり1フィートのときに行き過ぎたら失格でしょうかね。
ともあれネコに負けることになりそうです。
だけど向きを変えるのにどのくらいの時間がかかるんだろう。
向きを変えるのに時間がかかるなら結果が変わるときもあるしなあ。
どようなことになるか?
といういいまわしも微妙だなあ
まず この解答をおくっておこうっと...(*^_^*)

(ペンネ−ム:ネクター)
素直に解いてみました。
イヌ が2とびするあいだにネコは 3とびするということで
イヌの1とび3秒、ネコの1とび2秒とすると、6秒でどちら
も6フィート。
まず最初の100フィートを考える。
100割る6は16あまり4。残り4メートルまでは同時に到
着。さて残り4フィート。ネコは2とび。イヌは...やっぱり2と
び。イヌが2とびしてる間にネコはもう一回飛べるので折り返し。
6秒後には4フィートもの差がつく。
帰りは差がつかない。
往復するたびに4フィートずつ差をつけてネコの勝ち。

(ペンネ−ム:やなせ)
犬が一回当たり3フィートのジャンプを2回する間に
猫は一回当たり2フィートのジャンプを3回するので
速度的には両者は同じです。
そこで100フィート以内で2&3フィートの最大公倍数を
求めると96フィートになります。
つまり此処までは両者一歩も譲らず同着です。
さてここからですが両者とも決められた距離以外のジャンプは
出来ないものとすると残り4フィートを犬は2回
ジャンプして102フィート地点に着地しなければ
往路をクリアー出来ません
その間に猫は3回ジャンプできるので
内2回で往路100フィートクリア残る一回のジャンプで
復路の2フィートをクリアーします。この時点で
犬はスタート地点から102フィートの場所に居ますので
復路のスタートは猫=98フィート、犬=102フィートからの
同時スタートの形になります。
両者の残り距離から先ほどの最大公倍数を引くと
スタート地点から犬は6フィート、猫は2フィートまでは
同時に戻ってきます。猫は後一回のジャンプでゴール
出来ますが犬は2回必要なので、猫が先着します。
答え 猫先着です
連勝単式=猫−犬で配当金は75円です。(爆笑)
ただし猫が折り返し地点から3回目のジャンプを実行しないで 犬が2回目のジャンプ終わるまで待って、そこから 復路同時スタートとしてもやっぱりわずかの差ですが猫先着です。
おまけです
ジャンプの距離調整や途中障害物(たとえば深い溝)等が
無いものとして、又犬は高度な技(三角飛び)など出来なくて
しかもゴール地点にその技が利用できる壁などが無いものとして
考えてみました。
犬が猫を脅かして先着するって事も実際は有りがちかな
折り返し地点にマタタビを置いておけば犬が勝ちますよね(笑)

(ペンネ−ム:こざっぱ)
イヌが、3フィート×2回 = 6フィート 進む間に
ネコは、2フィート×3回 = 6フィート 進むので
両者の速度は同じ、よって同時にゴール。。。。。
といってはいけませんね。
イヌは1回に3フィート進みますので、33回とんで99フィート
34とび目に折り返し点を過ぎて102フィートのところで折り返します。
36とび目に96フィートの地点に戻ってきています。
一方、ネコは、イヌが34回とんで折り返し点を越えた時、51回とんで、
ます。ネコは、50回でちょうど100フィートで折り返せるので、51
とび目で98フィートの位置におり、イヌが96フィートの位置に戻って
来た36とび目には、ネコは、54とび目で、92フィートに戻っていま
す。両者の速度は同じですので、そのままネコが先にゴール。
ネコの勝ちとなります。
随分と寒くなってきました。これからはイヌは庭を走り回り、
ネコはコタツで丸くなる季節です。
この問題のようなシーンに出くわすのは来年暖かくなってからでしょうか。。

(ペンネ−ム:モルモット大臣)
今回はネコさんとイヌさんの片道100フィートの往復レースです。
よくトレーニングされた2匹ということでいろいろ考えさせられます。
そこでトレーニングの状況で答が違ってくるのではと考えました。
まずネコさんの3とびする時間とイヌさんの2とびする時間を6Tとすると
イヌさんの 1とびする時間は3T、ネコさんの1とびする時間は2Tとおける
そこで
1) イヌさんが1/3とびが出来る場合
イヌさんは99フィートまで33とびを行い辿り着き、その後1フィート進むために1/3と
びを行い、100フィート到達。その後同じく 99フィートまで33とびで行き
1/3とびを行い100 フィート到達して合計200 フィート到達。
よってイヌさんは全部で66+2/3=200/3とびするからこれに要する時間は
200/3×3T=200T
この時ネコさんは200 フィートを100とびでいけるからそれに要する時間は
100×2T=200Tで同時にゴールすることになる。
しかしこれはあまのじゃく的発想であるので
2) イヌさんが1/3とびが出来ない場合
イヌさんは34とびで100 フィートを一旦越え、同じ距離を戻ることになるから
イヌさんは34×2とびすることになりこれに要する時間は68×3T=204T
一方ネコさんの要する時間は前述と同じく200Tである。
よってこの勝負はネコさんの勝ちである。

(ペンネ−ム:杖のおじさん)
折返しのところで1度着地することから片道何とびするか計算して往復なので2倍して何とびでゴールするかを計算します。
次に、イヌの1とびの時間をxとし、ネコの1とびの時間をyとして、イヌ2とびとネコ3とびする時間は同じなのでその時間をtとすると
t=2x=3y イヌの1とびの時間 x=t/2
ネコの1とびの時間 y=t/3
イヌが何とびでゴールするか。
片道100÷3=33(1/3) 従って34とび往復なので34×2=68とび
ネコが何とびでゴールするか。
片道100÷2=50 往復なので50×2=100とび
イヌのゴールまでの時間は 68×(t/2)=34t
ネコのゴールまでの時間は 100×(t/3)=33(1/3)t
従ってネコの勝ちとなります。

(ペンネ−ム:浜田 明巳)
イヌよりネコが好きなので,ネコの勝ち,なんて冗談はさておき.
「イヌが2回とぶ間にネコは3回とぶ」という条件であるが,
これはネコがちょうど3回とぶとも解釈出来るし,3回以上4回未満とぶとも解釈出来る.
天下の小島先生が問題を間違えるはずがないので,どちらに解釈しても結果は変わらないはずである.このようにネコの移動速度が少し速くなっても答が同じであろうから,答はネコの勝ちであるはずである.なんて答も数学的に通用するはずがないので,改めてきちんと解きます.
時間をtで表す.よく仕込まれたイヌ,ネコなので,次のように仮定することが出来る.
スタート直前までには,第1ジャンプの体制を整え,スタート直後(t=0のとき),ジャンプするとする.
100フィート直前のジャンプにて,自分の最高ジャンプ距離で100フィートを越えてしまう場合,うまく調整して100フィートきっかりに着地出来るとする.
最高ジャンプ距離未満のジャンプをこれからする場合でも,した後でも,次のジャンプまでの休養時間は同じとする.
方向転換にかかる時間は0とする.
ジャンプにかかる時間は0とする.しかしこれは不自然かも知れない.スタート時点のt=0のときには,イヌは0フィート,3フィートの2箇所同時に存在し,ネコは0フィート,2フィートの2箇所同時に存在するのだから.しかし便宜上無視する.
イヌが2ジャンプするときに,ネコは3ジャンプするということから,イヌはtが3増加するごとにジャンプし,ネコはtが2増加するごとにジャンプするとしてよい.
このとき,0≦t≦201におけるイヌ,ネコの移動表(スタート地点からの距離の表)は,
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ・・・ | 96 | 97 | 98 | 99 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| イヌ | 3 | 3 | 3 | 6 | 6 | 6 | 9 | 9 | ・・・ | 99 | 99 | 99 | 100 | 100 |
| ネコ | 2 | 2 | 4 | 4 | 6 | 6 | 8 | 8 | ・・・ | 98 | 98 | 100 | 100 | 98 |
| t | 101 | 102 | 103 | 104 | 105 | ・・・ | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| イヌ | 100 | 97 | 97 | 97 | 94 | ・・・ | 7 | 4 | 4 | 4 | 1 | 1 | 1 | 0 |
| ネコ | 98 | 96 | 96 | 94 | 94 | ・・・ | 4 | 4 | 2 | 2 | 0 | 0 | 0 | 0 |
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ・・・ | 95 | 96 | 97 | 98 | 99 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| イヌ | 3 | 3 | 3 | 6 | 6 | 6 | 9 | 9 | ・・・ | 96 | 99 | 99 | 99 | 96 | 96 |
| ネコ | 2 | 2 | 4 | 4 | 6 | 6 | 8 | 8 | ・・・ | 96 | 98 | 98 | 99 | 99 | 97 |
| t | 101 | 102 | 103 | 104 | 105 | ・・・ | 192 | 193 | 194 | 195 | 196 | 196 | 197 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| イヌ | 96 | 93 | 93 | 93 | 90 | ・・・ | 3 | 3 | 3 | 0 | 0 | 0 | 0 |
| ネコ | 97 | 95 | 95 | 93 | 93 | ・・・ | 5 | 5 | 3 | 3 | 2 | 2 | 0 |
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ・・・ | 96 | 97 | 98 | 99 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| イヌ | 3 | 3 | 3 | 6 | 6 | 6 | 9 | 9 | ・・・ | 99 | 99 | 99 | 101 | 101 |
| ネコ | 2 | 2 | 4 | 4 | 6 | 6 | 8 | 8 | ・・・ | 98 | 98 | 100 | 100 | 101 |
| t | 101 | 102 | 103 | 104 | 105 | ・・・ | 198 | 199 | 200 | 201 | 202 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| イヌ | 101 | 98 | 98 | 98 | 95 | ・・・ | 2 | 2 | 2 | 0 | 0 |
| ネコ | 101 | 99 | 99 | 97 | 97 | ・・・ | 4 | 4 | 2 | 2 | 0 |
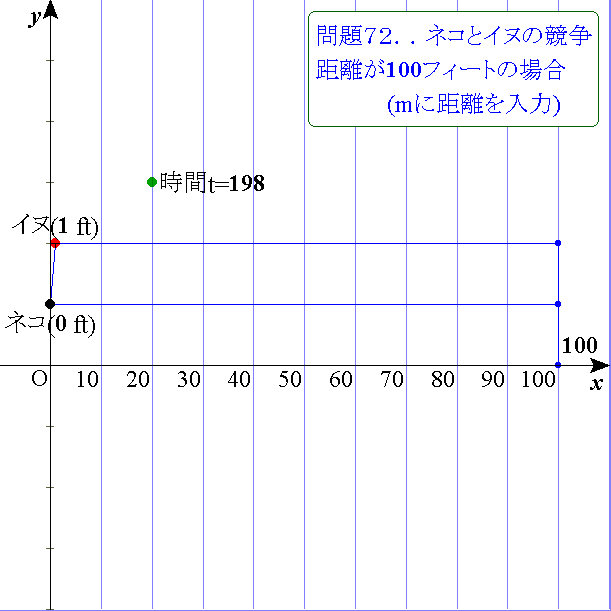
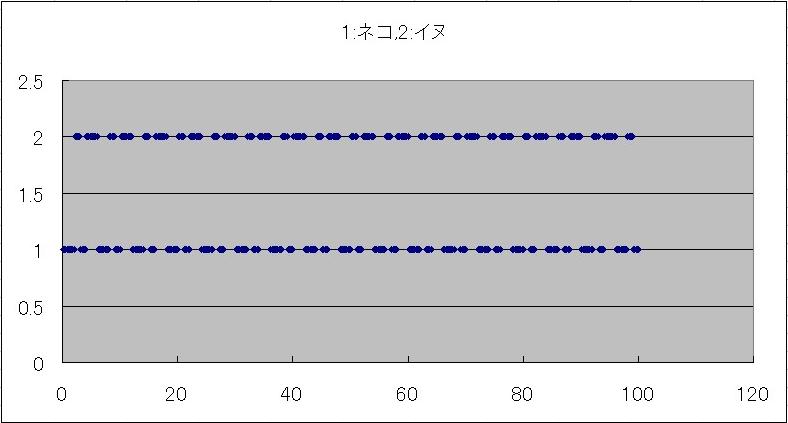
いろいろな距離に対するイヌ,ネコの対戦結果を計算してみました.
距離をlフィートとするとき,0<l≦100の範囲で,
6n<l≦6n+2,6n+3<l≦6n+4のとき,ネコ
6n+2<l≦6n+3,6n+4<l≦6(n+1)のとき,イヌ
(n=0,1,2,3,・・・)
のそれぞれの勝ちとなり,引き分けはありませんでした.対戦結果は互角です.
問題の100フィートは,n=16のときであり,確かにネコの勝ちです.
lが6の倍数のとき,同着のように思えますが,よく仕込まれたイヌ,ネコなので,スタート直前までに第1ジャンプの準備は整っているはずです.ジャンプの準備はイヌ,ネコそれぞれ3,2かかるので,その差1の分だけイヌが有利になるのです.「よく仕込まれた」という条件はこんなにも重要なのですね.でもネコってそんなに仕込めるのかな? 不安になってきた.
Sub Macro2()
Sheets("Sheet2").Select
Dim d_dog As Double
Dim d_cat As Double
Dim dog As Double
Dim cat As Double
Dim t As Integer
Dim kyori As Double
Dim kizami As Double
Dim owari As Integer
Dim kekka As Integer
Dim gyou As Integer
kizami = 0.2
For gyou = 1 + 1 To 100 * 5 + 1
If gyou = 1 + 1 Then
Cells(2, 1).Value = kizami
Else
Cells(gyou, 1).Value = Cells(gyou - 1, 1).Value + kizami
End If
kyori = Cells(gyou, 1).Value
t = 0
dog = 0
cat = 0
d_dog = 3
d_cat = d_dog * 2 / 3
owari = 0
While owari = 0
If t Mod 3 = 0 Then
dog = dog + d_dog
If d_dog > 0 And dog >= kyori Then
d_dog = -d_dog
dog = kyori
End If
If d_dog < 0 And dog <= 0 Then
dog = 0
owari = 1
End If
End If
If t Mod 2 = 0 Then
cat = cat + d_cat
If d_cat > 0 And cat >= kyori Then
d_cat = -d_cat
cat = kyori
End If
If d_cat < 0 And cat <= 0 Then
cat = 0
owari = 1
End If
End If
t = t + (1 - owari)
Wend
If dog = 0 And cat > 0 Then
kekka = 2
ElseIf dog > 0 And cat = 0 Then
kekka = 1
Else
kekka = 0
End If
Cells(gyou, 2).Value = kekka
Range("A" & gyou).Select
Next gyou
Range("A1").Select
End Sub

(ペンネ−ム:小学名探偵)
答えネコの勝ち。イヌを4フィート離してネコがゴールイン。
3×33<100<3×34=102 ワンちゃんは102+102を68飛びでゴールイン。アンラッキー。
2×50=100 ニャンちゃんは100+100を100飛びでゴールイン。ラッキー。
速さは同じだけれど着地点が飛び飛びだから道のりの差(204−200=4)だけ差がつきます。、
ネコの折り返し点からネコはゴールに向かって行くのにイヌは2フィート分ゴールから離れる方向に進んでから折り返すからここのところで(イヌが折り返した時点で)2+2の差がつきます。
| 片道の長さが | 6の倍数ならネコとイヌの | 差は0. |
| 6の倍数+1なら | 差は2. | |
| 6の倍数+2なら | 差は2 | |
| 6の倍数+3なら | 差は−2。 | |
| 6の倍数+4なら | 差は4. | |
| 6の倍数+5なら | 差は0. |
連続した量で考えると、片道の長さをXとし、nを整数とすると、
| 6×n<X≦6×n+2 | のときネコとイヌの | 差2 |
| 6×n+2<X≦6×n+3 | 差−2 | |
| 6×n+3<X≦6×n+4 | 差4 | |
| 6×n+4<X≦6×n+6 | 差0 |
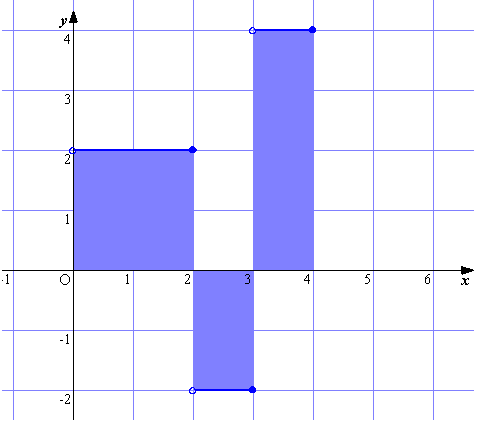
片道の長さX=6×n+x (0<x≦6)、復路に折り返した時にネコのリードする距離y (フィート)とすると、このようなグラフになりますでしょうか? (Junko)

(ペンネ−ム:kirkland)
先生「今回は、年末スペシャルということで、みんなで考えよう。意見がある人は手を挙げて。」
B君「は〜い。イヌが6フィート進む間にネコも6フィート進むので、同着だと思いま〜す。」
C君「オレもその意見に賛成だぜ。」
Dさん「え〜、そんな単純でいいの?」
A君「イヌは、3フィートずつ進むんだから、折り返し地点を通り過ぎるんじゃないかな。ネコは、2フィートずつ進むから、ちょうど折り返し地点に着いて、無駄な部分がないだろ。だからネコの勝ちだよ。」
Eさん「さすが、A君。でも、もう終わってしまうのは寂しいわね。」
C君「おいA、分かったからって、いい気になってんじゃないぞ!」
A君「何だよ!文句あんのかよ!」
C君「おーっ!やるかぁ!?」
 Dさん「あんたたち、やめなさいよ。だいたいC君は、乱暴すぎるわよ。
今日も掃除当番サボったでしょう!」
Dさん「あんたたち、やめなさいよ。だいたいC君は、乱暴すぎるわよ。
今日も掃除当番サボったでしょう!」
C君「うるせえ!どブス!」
B君「ところで、どうやって折り返すのかなぁ?」
C君「オレに、いい考えがあるぜ。折り返し地点の先は、断崖絶壁になっていて、イヌは谷底へ転落するってのはどうだ!
これぞ、まさしく『犬死に』だ!がっはははっー!(図1)」
 Eさん「イヌがかわいそうよ。」
Eさん「イヌがかわいそうよ。」
Dさん「C君は、野蛮すぎるわよ。すぐに、女の子の髪の毛を引っ張るし。」
A君「しかし、下手な絵だな。幼稚園児でももう少しうまいぞ。」
C君「うるせえよ!お前らに、オレ様の芸術が分かってたまるか!」
B君「今思ったんだけど、折り返し地点が壁だったら、ネコは、
ピッタリ壁にくっついて身動きとれないんじゃないのかなあ?(図2)」
 C君「それじゃあ、イヌは壁に激突して、やっぱり『犬死に』だぜ!」
C君「それじゃあ、イヌは壁に激突して、やっぱり『犬死に』だぜ!」
Dさん「なんでC君は、そんな残酷なことしか思いつかないわけ?
今日も、Eちゃんのスカートをめくったでしょう!」
Eさん「私、お嫁に行けないわ。シクシク…」
C君「ざまあみろ!ブ〜ス、ブ〜ス!」
A君「よく仕込まれたネコだから、空中で体を反転させることぐらい
できるんじゃないのかなぁ?」
B君「イヌはどうするんだろ?」
A君「壁で反射(?)して、三角飛びだよ。きっと。(図3)」
Dさん「なんか、何でもありになってきたわね。」
C君「オレはよぉー、イヌは途中で棒に当たるので負けると思うぜ。」
Eさん「ネコは、こたつで丸くなっているので、イヌの勝ちだと思うわ。」
B君「ネコはネズミに騙されて、1月2日の朝にゴールしたので、ネコの負けだよ。」
C君「オレは、ネコまんまが好きだぞ。」
Dさん「あんた、今日の給食でニンジン残したでしょう!」
B君「あのねQ太郎はね、イヌにはとっても弱いんだってさ」
A君「おいC、ハリーポッターのビデオ返せよ。」
C君「いやだね!『お前の物はオレの物、オレの物はオレの物』だ」
Eさん「うちのポチは、とってもかわいいのよ。」
A君「来月は2003に関する問題かなぁ?2003は素数なのに、小島先生どうするんだろう?」
先生「あとは、君たちで勝手にやっときなさい!先生は、忘年会に行って来るぞ!」
小島 (特別出演) C君、ことばには気を付けて!

(ペンネ−ム:Toru)
スピードが変化する場合は、イヌが2とびの間にネコが3とび、という条件をみたし
難くなるため、スタートから一定の速度で進むものとして考えました。
ネコは条件通り進んで50とびで100フィート地点に達し、向きをかえて再び50
とびでゴールすると考えられます。すなわち所要時間は(100とび分の時間+向き
をかえる時間)ということになります。
イヌの場合は、2通り考えられて、
1)34とびで102フィート地点に達し、そこで向きをかえて、また34とびでゴールする場合、これは68とび分の時間+向きを
かえる時間となりますが、向きをかえる時間が同じとすればこれでは当然ネコに勝て
ません。 そこで
2)33とびで99フィート地点に達したところで(あるいはこの
空中で)向きをかえて、後ろ足で100フィート地点をキックする(水泳のターンの
要領)、この場合は復路は34とび目の空中(1/3とんだところ)でゴールを迎え
ることになるかと思います。この所要時間は(66とび+1/3とび)分の時間+向
きをかえる時間。やはり向きをかえる時間が同じとすれば、(66+1/3)X3/
2=199/2でこれならネコに勝てる可能性があります。ただし後ろ足を出す分、
向きかえにやや時間を要するかも知れないのでここを素早くやることが肝腎です。な
らばネコも98フィート地点で向きをかえればというのは、1とび、と飛んでやっと
2フィートなので、2フィート先に後ろ足は届かないと考えてよいと思います。
以上より、多分ネコが勝つがターンの練習によってはイヌにも勝機あり、ということ
になるかと思います。

(ペンネ−ム:teki)
答え ネコの勝ち
<理由>
単位時間に進む距離はイヌもネコも同じですが、100フィートの
直線の往復では、折り返し点で、ネコは丁度100フィートで折り返す
ことができますが、イヌは99フィート地点であと3フィート跳ばなけれ
ばならず、結局102フィートの往復となります。
よって、ネコの方が2跳び分早くゴールします。
<追加解答1>
イヌは、前回の方法では負けることが分かったので、ネコに言いました。
イヌ:「もう1回、競争しようよ。」
ネコ:「いいよ、何度でもやってみよう。」
イヌは、今度は99フィート進んだ地点でUターンしました。
すると、イヌのしっぽが折り返し点を横切り、うまく折り返せました。
結局、ネコは負けてしまいました。
<追加解答2>
ネコ:「あんなの、ずるいよ。もう1回競争しよう。」
イヌ:「いいよ。」
ネコは、今度はイヌがやった方法で、折り返し点の手前でUターンしました。
ところが、98フィート地点でUターンしたところ、ネコのしっぽは折り返し点
に届いておらず、結局、ネコは反則負けになってしまいました。
結果はイヌの2勝1敗でした。ちゃんちゃん。
注)1フィートは12インチで、約30.5cm です。
この程度なら、イヌの場合、前足からしっぽまでの長さで十分折り返し
点に到達できますが、ネコの場合は、2フィート=約61cmとなり、よっ
ぽど大きなネコでない限り、無理でしょうね。

| こざっぱ | teki | 巷の夢 |
| やなせ | モルモット大臣 | Toru |
| AK | 理一郎ぼちゃん | 杖のおじさん |
| 浜田 明巳 | 小学名探偵 | 夜ふかしのつらいおじさん |
| エルトシャン | 高橋 道広 | 暇人 |
| kirkland | 天才小学生Mappy | リナライ |
| 三角定規 | ネクター | Banyanyan |

今回もたくさんの解答をどうもありがとうございました。 なかなかユーモラスな解答も多く、読ませていただきながら笑ってしまいました。
「イヌは1とびで3フィート、ネコは2フィート進むが、イヌが2とびするあいだにネコは 3とびする。」 これだけですと、なーんだ同じと思われるかもしれません。 確かに直線コースでは差がつきません。 「100フィートの直線コースを往復競争する。」 というのがポイントになります。 多くの方にご指摘いただきましたように、ネコはきっちり100フィートで折り返すことができますが、イヌは飛び出してしまいます。 それがロスとなって、結局イヌが負けてしまうということになります。 小回りのきくネコが有利ということでしょうか。
でも、実はコースによっては、イヌが勝つ場面もあります。 小学名探偵さんがコースと勝敗との関係を考察してくださいました。 平均的にはネコが有利ですが、イヌが勝つケースもあります。
今回一番笑えたのが、Toruさんとtekiさんですね。 Uターンの仕方によっては、イヌにも勝つチャンスがある!(イヌのしっぽは大事にしよう)

 E-mail
E-mail
 戻る
戻る
 top
top