Weekend Mathematics／問題／問題7

７．卵の問題

卵が６個入るパックと、 このパックが６パック入る箱があり、 この箱が６箱入る段ボ−ル箱があります。
それぞれいっぱいになるごとに、 パックから箱に、箱から段ボ−ルに、と入れていきます。
今、この方法でいくつかの卵を詰めるとき、 いっぱいに入っている段ボ−ル箱、箱、パックの数と余りの卵の数を ［　］［　］［　］［　］に左から順に書き入れる事にします。
箱などが空の場合や余りの卵がない場合には０と書きます。
例えば、４８個の卵を詰めるとすると、 段ボ−ル箱０、箱１、パック２、余りの卵０となり、 ［０］［１］［２］［０］です。
次の問に答えなさい。

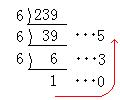
（１）２３９個の卵を詰めると、［　］［　］［　］［　］とかけます。

（２）［１］［３］［０］［２］と書ける卵の個数はいくつでしょう。

（３）［０］［５］［０］［５］とかける卵の個数と、 ［１］［５］［１］［５］と書ける卵の個数との和は［　］［　］［　］［　］とかけます。

（４）段ボ−ル箱６つの入るコンテナを持ってきて、 卵の数をいっぱいに入っているコンテナ、段ボ−ル箱、箱、パックの 数と余りの卵の数を左から並べて［　］［　］［　］［　］［　］ としましょう。
この時、［０］［０］［１］［３］［１］と書ける卵の個数と、 ［０］［０］［１］［２］［３］と書ける卵の個数との積の個数を、 またこれらの容器に詰め直すと、［　］［　］［　］［　］［　］となります。

問題の出典

(2)を除く

慶應義塾中等部'93

パズルより面白い中学入試の算数

ピ−タ−・フランクル

講談社

答えと解説

答えと解説

(1)回答・その１

（ペンネ−ム：ミネラル　ＷＡＴＥＲ）

卵６個＝１パック

卵３６個＝６パック＝１箱

卵２１６個＝３６パック＝６箱＝１ダンボ−ル

ダンボ−ルの方から考える。
２３９個−ダンボ−ル１箱（２１６個）＝２３個
２３個−３パック（１８個）＝５個
［１］［０］［３］［５］

(1)回答・その２

（ペンネ−ム：ＢＡＢＹ　ＭＩＮＮＩＥ）

パックは卵が６個入る。
箱は卵が３６個入る。
段ボ−ルは卵が２１６個入る。

まず、２３９個は２１６個を越えているので段ボ−ル箱が１つできる。
２３９−２１６＝２３
２３個では箱をいっぱいにできないのでパックにつめると
２３÷６＝３・・・５
よって、［１］［０］［３］［５］とかける。

(２)回答

（ペンネ−ム：ｅｓ）

段ボ−ルは２１６×１＝２１６

箱は　　　　３６×３＝１０８

パックは　　　６×０＝　　０

あまりは　　　　　　　　　２

よって、２１６＋１０８＋２＝３２６個

　　　　　　　　　　　

(３)回答・その１

（ペンネ−ム：ドロシ−）

［０］［５］［０］［５］＋［１］［５］［１］［５］
=(0×216+5×36+0×6+5)+(1×216+5×36+1×6+5)
=(180+5)+(216+180+6+5)
=185+407
=592個

段ボ−ル　５９２÷２１６＝２・・・１６０より２個

箱　　　　１６０÷３６＝４・・・１６より４個

パック　　１６÷６＝２・・・４より２個

余り　　　４個 　
従って、［２］［４］［２］［４］

(３)回答・その２

（ペンネ−ム：未定）

［０］［５］［０］［５］＋［１］［５］［１］［５］
＝［１］［１０］［１］［１０］
＝［２］［４］［２］［４］

(４)回答

（ペンネ−ム：S.I.）

（４）［０］［０］［１］［３］［１］X［０］［０］［１］［２］［３］
＝（6²×1 +6×3+1)×（6²×1+6×2+3）
＝6⁴×1+6³×2+6²×3+6³×3+6²×2×3+6×3×3+6²×1+6×2+3
（整理すると）
＝6⁴×1+6³×5+6²×10+6×11+3
（6×11＝6×6+6×5＝6²×1+6×5だから）
＝6⁴×1+6³×5+6²×10+6²×1+6×5+3
＝6⁴×1+6³×5+6²×11+6×5+3
（6²×11＝6²×6+6²×5
　＝6³×+6²×5だから）
＝6⁴×1+6³×6+6²×5+6×5+3
（6³×6＝6⁴×だから）
＝6⁴×2+6²×5+6×5+3
＝［2］［０］［5］［5］［3］

正解者（ペンネ−ム）

S.I.

matheman

ＢＲＡＩＮＭＡＮＩＡ

ミネラル　Ｗａｔｅｒ

ＢＡＢＹ　ＭＩＮＮＩＥ

ＦＬＡＳＨ！

みなみのしゅういち

コレクトコ−ルは１０６番！

凡人。

匿名希望

ｅｓ

ドロシ−

！？

まとめ

今回は６進法の問題でした。

（１）まず、１０進数を６進数に直すには、 次のように６で割っていくといいのです。

（２）逆に６進数を１０進数に直します。
６進数は下から、１の位、６の位、６^２の位、６^３の位 ですから、
１×６^３＋３×６^２＋０×６＋２×１＝３２６
　　 とすればいいわけです。

（３）ドロシ−さんのように、一端１０進数に直して演算し、 それをまた６進数に直すというのも１つの手ではあります。
でも、できれば直接やりたいですよね。普通の縦書きの足し算と同様にできます。 ただ、表記する時に６進数にすればいいのです。

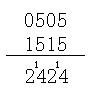
（４）次はかけ算です。これも、縦書きでやってみましょう。 足し算と同様に、表記はあくまで６進数です。

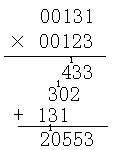
参考のために６進数の五五（九九をもじって）を示しておきましょう。

６進法の五五

	１	２	３	４	５
１	１	２	３	４	５
２	２	４	１０	１２	１４
３	３	１０	１３	２０	２３
４	４	１２	２０	２４	３２
５	５	１４	２３	３２	４１

私たちが普段使っている数体系はもちろん１０進法ですけれども、 これは人間の指が１０本であることと無縁ではありません。 もし、人間の指が６本だったら、６進法の世界になっていたと思います。 人間の指が８本だったら、コンピュ−タ−の進化はもっと早かっただろうという人もいます。 コンピュ−タ−では、ある（１）、ない（０）を 組み合わせて数値を表現する２進法が使われています。 ２進法を３桁ごとに区切ると８進法だから、というわけです。

さて、身のまわりには１０以外の基数が使われている例があります。
時刻を計る時の６０進法です。１時間が６０分に、１分が６０秒に分割されています。 これは、紀元前２０００年ごろのバビロニア人の方式です。 バビロニア人は、まず大きな単位を決め、それを分割して小さい単位を決めていったようです。 しかし、基数に柔軟性がなくてはこういう分割はできません。 １０という数は２と５しか約数に持たないのに対して、 ６０は、２、３、４、５、６、１０、１２、１５、２０、３０と１０個もの約数を持ちます。 １０進数では、３で割るといことが厳密にはできませんけれども、６０進法ではできるわけです。 確かに、１時間に３つの問題を解かなければならないような試験で、 １題２０分だなとすぐ計算できるのは６０進法のおかげかもしれません。

円を３６０等分するというのもバビロニアに起源を発するものだそうです。 １本のロ−プを３等分し、それで三角形を作ります。（正三角形） この三角形の角度を単位として、それを６０等分したものを１度としたわけです。 さらに６０等分したものを「分」、さらに６０等分したものを「秒」としたわけです。
円が３６０度というのは、円の中に正三角形がぴったり６個入るという事実からきているわけです。

さて、もう１つ１２進法というのがあります。 （ついビ−ル１ダ−スを連想してしまうのですが・・・。）
１年を１２ヶ月に分けているのは、地球をまわる月の運行と関係ありですね。 １年というのは地球が太陽をまわる公転周期です。 これが、ほぼ１２ヶ月というわけです。 だから、太陽の軌道も１２宮に分けられているわけです。 １日が１２時間の２倍になっているのも同様に１２という数を好んだからでしょうか。

ところで、中国には古くから十干十二支というのがあります。略して干支（えと）。
十干とは、甲、乙、丙、丁、戊、己、庚、辛、壬、癸。
日を数える数詞として使われていたとのことです。 まさしく、指折り数える１０進数。

十二支とは、子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥。
こちらは、月を数える数詞だったようです。
この十二支をのちに「十二獣」に配当したのは、中国の戦国時代（紀元前４０３〜前２２１） ともいわれています。抽象的な文字になじまない庶民に分かりやすいように、 身近な動物を選んでそれぞれに配当したのでしょう。
十二獣の名称
子（鼠）、丑（牛）、寅（虎）、卯（兎）、辰（龍）、巳（蛇）、 午（馬）、未（羊）、申（猿）、酉（鶏）、戌（犬）、亥（猪）。
十二獣の中に最も身近な猫が入っていない理由について面白い説話があります。 天帝が動物たちを呼び集め、 期日を定めて到着順に十二支を与えるという布告を出した。 猫はその布告が出たとき眠っていて知らなかった。 猫が仲の良い鼠に日時を聞くと、 鼠は期日の翌日を猫に教えた。 いよいよ当日、動物たちはねぐらを出て天帝の館へ急ぎ馳せ、 鼠、牛、虎・・・の順に到着してそれぞれ十二支が与えられた。 それとも知らず猫は翌朝早く目を覚まして天帝の前に出たが、 勝負は昨日終わったことを知らされ、十二支が与えられなかった。 鼠にだまされたことを知った猫は、 以来鼠を恨んで捕らえるようになったといいます。

十二支はまた、方位にも配当されました。

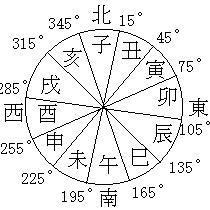
さらに、十二支は時刻にも配当されています。

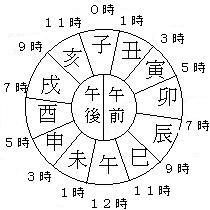
午の刻の真ん中の時刻が「正午」で、 正午を境にしてその前を「午前」、 その後を「午後」というわけです。

十干と十二支を組み合わせると、 １０と１２の最小公倍数６０の組み合わせができます。 これを「六十干支」といいます。 干支を年月日に割り当て、暦に取り入れたのは、 漢の武帝紀元前１０４年「太初歴」が最初、 日本では、西暦６０２年推古天皇のとき、 百済より暦本が輸入され、 その２年後の６０４年に暦日が採用されて「甲子の年」と定められたとのことです。 この時以来今日まで、年の干支は連綿と続いています。
高校野球で知られる甲子園が、甲子（きのえね）の年（１９２４年）に完成したことから 命名されたというのは有名な話ですね。
壬申の乱（６７２年）や、戊申戦争（１８６８年）など 歴史的事柄の名前にも六十干支が使われています。
今年は「丁丑（ひのとうし）」に当たります。
そして、「還暦」というのは、生まれの干支に還るという意味で、 ６０年たつともとの干支に戻る６０才をお祝いするものですね。

洋の東西を問わず、どうやら１０、１２、６０がkey number のようです。

参考
Ｃ．ランツォス著「数とはなにか」講談社ブル−バックス
永田久著　ＮＨＫ市民大学「時と暦の科学」

戻る