Weekend Mathematics/問題/問題68
68.棒を立てる問題
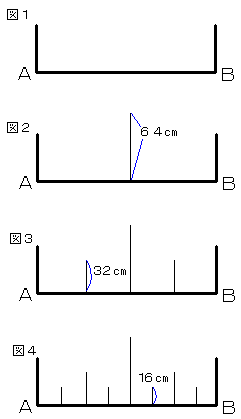
A,B2つの地点をまっすぐな線で結び、この線の上に次のようにして棒を立てます。
1.A,Bの2つの地点に目印の棒を立てる。(図1)
2.A,Bのまん中の地点に64cmの棒を立てる。(図2)
3.2つの棒にはさまれたまん中の地点に32cmの棒を立てる。(図3)
4.2つの棒にはさまれたまん中の地点に16cmの棒を立てる。(図4)
以上の作業を(1/16)cmの棒を立てるまでくりかえします。そのあと目印の棒2本をとりのぞいて作業を
終わります。ただし立てる棒の長さは、2→3→4→・・・と進むごとに半分になるものとします。
問1.(1/4)cmの棒は何本立っていますか。
問2.立っている棒全部の長さの和は何cmですか。
問3.Aの方から2000番目の棒の長さは何cmですか。
問題の出典
ピーター先生と中学入試の算数に挑戦!
ピーター・フランクル
新潮社
土佐中学校2001年度入試
答えと解説

答えと解説
解答・その1
(ペンネ−ム:スモークマン)
1. 2の6乗〜2の-4乗まで。二乗が一つ下がるごとに、2倍ずつ本数が増えるから、
6-(-2)=8より、2の8乗=256本。
2. 大きさが1/2になるが、本数は、2倍になるため、
合計では、64cm。だから、64x11=704cm。

解答・その2
(ペンネ−ム:モルモット大臣)
今回は時間がなく解答だけで失礼します。
(1) 256 本
(2) 704 cm
(3) 1 cm

解答・その3
(ペンネ−ム:やなせ)
問い1、(1/4)cmの棒は何本立っていますか?
棒の長さが半分になるときには棒の本数は2倍になっていきますので
64→32→16→8→4→2→1→1/2→1/4・・・なので
1*2*2*2*2*2*2*2*2で2の8乗=256本です
問い2、立っている棒全体の長さの和は何cmですか?
問い1の答えを求める式?から各長さの本数は
64→1。32→2。16→4・・・・・1/16→1024です
おわかりのように各長さに各本数を掛け合わせた長さは
いずれの場合も64cmになります、棒の種類は11種類になるので
64cm×11=704cmになります。
問い3、Aの方から2000番目の棒の長さは何cmですか?
各棒の本数を合計すると
1+2+4+8・・・・・・・256+512+1024=2047
Aから2000番目はBの方からは48番目になります
ここからが私らしくしこしこと(いつもこればっかり、でも報われなくて間違いも多いのですが)
やりましたところ長さ1cmの棒が立っていました
お答えは1cmです

解答・その4
(ペンネ−ム:ドラ)
まず、問題より、
64cmの棒は1本
32cmの棒は2本
16cmの棒は4本
・
・
・
(1/16)cmの棒は1024本
つまり、棒の長さは
初項64, 公比1/2, 項数11の等比数列 ・・・(1)
棒の本数は
初項1, 公比2, 項数11の等比数列 ・・・(2)
のようになることは明らか。
問1
(解)
(1)より、9番目にできる棒が1/4になるので、
その棒の本数は(2)より、512本。
問2
(解)
64×1+32×2+・・・・・・とやっていってもよいが、
結局は64を11回足すことになると途中で気づくので、
64×11=704
問3
(解)
(2)と等比数列の和の公式より、すべての棒の本数は2047。
ここで、この図は64cmの棒について対称な図形になっているから、
Aから2000番目の棒の長さ=Bから48番目の棒の長さ=Aから48番目の棒の長
さである。
次に、Aに近い部分の図だけを書いてみる。
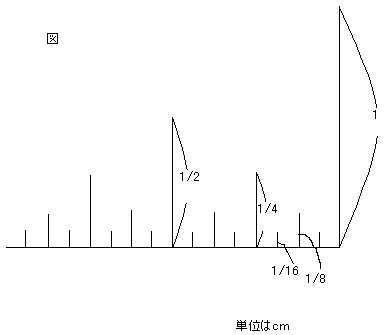
すると、最も左にある1/2cmの棒よりも左には、7本の棒がある。
そして、最も左にある1cmの棒よりも左は、
1/2の棒をに関して対称になっており、15本の棒がある。
同様に最も左にある2cmの棒よりも左には31本の棒がある。
2cmの棒よりも右には図のような棒の配置になる。
2cmの棒はAから32本目だから、
2cmの棒の右隣にある1cmの棒はAから48番目。
よって、Aの方から2000番目の棒の長さは1cm。

解答・その5
(ペンネ−ム:こざっぱ)
問1.(1/4)cmの棒は何本立っていますか。
棒は、半分の長さになるたびに、本数は倍になって行くので、
結局、同一の長さの棒の長さの合計は常に64cmになります。
なので、長さ1/4cmの長さの棒の本数は、
64 ÷ 1/4=256[本] です。 A.256本
問2.立っている棒全部の長さの和は何cmですか。
各長さとその本数の関係は以下の通りです。
| 長さ | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 1/2 | 1/4 | 1/8 | 1/16
|
|---|
| 本数 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024
|
|---|
| 全体本数 | 1 | 3 | 7 | 15 | 31 | 63 | 127 | 255 | 511 | 1023 | 2047
|
|---|
それぞれの長さにおける本数と長さの積は常に64cmですので、棒全部の長さの和は、
64 × 11 = 704 cm A.704cm
問3.Aの方から2000番目の棒の長さは何cmですか。
この問題が良くわからないのですが。。。。
棒は、真ん中に64cmが一本立っていて、左右対称で、本数が2047本なので、
Aから2000番目の棒は、Aから48番目の棒と同じ長さのはずです。
あとは、48番目の棒の長さを力作業で数えてみました。
一番、Aに近いのは、1/16cmの棒で、2番目は1/8cmの棒、のように考えると、、
1/16の棒は 1,3,5,7,9,11,13・・・・番目
1/8の棒は 2,6,10,14・・・・・・・・・・番目
1/4の棒は 4,12,20・・・・・・・・・・・・番目
48番目は長さ1cmの棒になります。 A.1cmの棒

解答・その6
(ペンネ−ム:柿本 浩)
(共通解)
問題の通りに棒を並べていくと、64cm:1本、32cm:2本、16cm:4
本、・・・と
手順を進める毎に棒の長さは前の半分、本数は前の2倍になっていく事が分かるので
1/16cmになるまでの、それぞれの長さの棒(便宜上a〜kのアルファベットで
表す)の本数は
| (a) | 64cm | :1本
|
| (b) | 32cm | :2本
|
| (c) | 16cm | :4本
|
| (d) | 8cm | :8本
|
| (e) | 4cm | :16本
|
| (f) | 2cm | :32本
|
| (g) | 1cm | :64本
|
| (h) | 1/2cm | :128本
|
| (i) | 1/4cm | :256本
|
| (j) | 1/8cm | :512本
|
| (k) | 1/16cm | :1024本
|
だと分かる。
問1.
共通解より、1/4cmの棒(i)は256本となる。
問2.
共通解のa〜kの棒で、長さ×本数の合計を取れば良いのだが
a→b、b→cと進む毎に長さが1/2倍、本数が2倍となっていくため
長さと本数の積は変化しない事に気づく。つまりa〜kまでの全ての棒は
長さ×本数=64であり、その合計は64×11=704cmだと分かる。
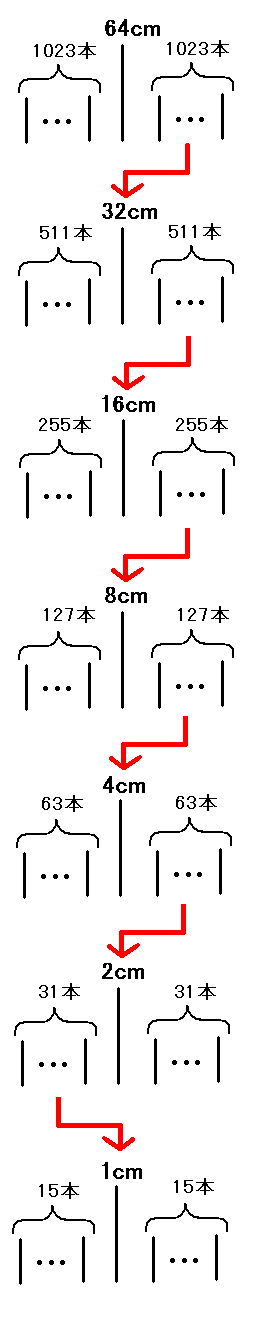
問3.
共通解より、a〜kの棒を全て合計すると2047本であり
「Aから数えて2000番目の棒」=「Bから数えて48番目の棒」だと分かる。
ここで、棒の並び順を考えてゆくと(以下図参照)
・2047本の中央にあるのはaの棒で、その両側に1023本ずつの棒が並んでいる
→ aの右側の1023本を考えると、中央にあるのはbの棒で、その両側に511本ずつの棒が並んでいる
→ bの右側の511本を考えると、中央にあるのはcの棒で、その両側に255本ずつの棒が並んでいる
→ cの右側の255本を考えると、中央にあるのはdの棒で、その両側に127本ずつの棒が並んでいる
→ dの右側の127本を考えると、中央にあるのはeの棒で、その両側に63本ずつの棒が並んでいる
→ eの右側の63本を考えると、中央にあるのはfの棒で、その両側に31本ずつの棒が並んでいる
つまり、この“31本・f・31本”が、最も右側(最もB寄り)の63本の棒の並
びなので
「Bから数えて48番目の棒」は「このfの棒の左側にある31本のうち、右から数
えて16番目の棒」だと分かる。
→ fの左側にある31本を考えると、中央にあるのはgの棒で、その両側に15本
ずつの棒が並んでいる
よって、この31本の中で右から16番目の棒は、31本の中央にあるgの棒だと分
かる。これが即ち「Aから2000番目の棒」であり、その長さは1cmである。

解答・その7
(ペンネ−ム:岡田)
まず、すべての立っている棒の数を数える。
長さは1/2ずつ短くなり、数は2倍ずつ増えるから。
(64cm 1本)、(32cm 2本)、(16cm 4本)、(8cm 8本)、(4cm 16本)、
(2cm 32本)、(1cm 64本)、(1/2cm 128本)、(1/4cm 256本)、
(1/8cm 512本)、(1/16cm 1024本)となる。
(1) 256本
(2) それぞれの棒の長さと数をかけた数はすべて64cmになる。
これがこれが11本あるので、棒全部の長さの和は704cmとなる。
(3) それぞれの立っている棒の間隔を式にすると、
1/16cmがy=2x-1、 1/8cmがy=4x-2、 1/4cmがy=8x-4、……と、
決まった変化をする式になる。これから、yが2000となる式をさがすと、
1cmのy=32x-16のときで、yに2000を代入するとxが63となる。
よって答えは1cm

解答・その8
(ペンネ−ム:勝浦捨てる造)
ABのまん中に、64cmの棒を1本立てると2分割される。その2分割されたそれぞれの
中央に32cmの棒を1本ずつ立てると4分割され、その4分割されたそれぞれのまん中に16cmの
棒を1本ずつ立てると8分割される。
以下同様の操作を1/16cm棒を立てるところまで行うと以下の表のようになります。
| 64cm棒 | 1本立てる | ABを2分割
|
| 32cm棒 | 2本立てる | ABを4分割
|
| 16cm棒 | 4本立てる | ABを8分割
|
| 8cm棒 | 8本立てる | ABを16分割
|
| 4cm棒 | 16本立てる | ABを32分割
|
| 2cm棒 | 32本立てる | ABを64分割
|
| 1cm棒 | 64本立てる | ABを128分割
|
| 1/2cm棒 | 128本立てる | ABを256分割
|
| 1/4cm棒 | 256本立てる | ABを512分割
|
| 1/8cm棒 | 512本立てる | ABを1024分割
|
| 1/16cm棒 | 1024本立てる | ABを2048分割
|
ところで、たてる棒の長さは、64→32→16→8→4→・・・→1/8→1/16と1/2になっているが、
棒の本数は、1→2→4→8→・・・と2倍ずつになっているので、結局は各棒の総全長(?)は
、64cmで一定です。
問1
64÷(1/4)=256(本)
問2
棒の長さの違う種類は11なので、64×11=704(cm)
問3
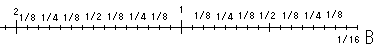
これは、64本立てた1cm棒のうちの一番右端に立てた1本付近
の拡大図です。
図から一番右端の1/16cm棒は、
1番目→3→5→7→9・・・と並んでいるからn番目は2nー1
1/8cm棒は、2→6→10→14→18・・・2(2n−1)
1/4cm棒は、4→12→20→28・・・22(2n−1)
1/2cm棒は、8→24→40→56・・・23(2n−1)
以上のことから、1cm棒から64cm棒までは次のように予想されます。
立てた棒の各々のn番目
| 1/16cm棒 | 2nー1
|
| 1/8cm棒 | 2(2n−1)
|
| 1/4cm棒 | 22(2n−1) すなわち 4(2n−1)
|
| 1/2cm棒 | 23(2n−1) すなわち 8(2n−1)
|
| 1cm棒 | 24(2n−1) すなわち 16(2n−1)
|
| 2cm棒 | 25(2n−1) すなわち 32(2n−1)
|
| 4cm棒 | 26(2n−1) すなわち 64(2n−1)
|
| 8cm棒 | 27(2n−1) すなわち 128(2n−1)
|
| 16cm棒 | 28(2n−1) すなわち 256(2n−1)
|
| 32cm棒 | 29(2n−1) すなわち 512(2n−1)
|
| 64cm棒 | 210(2n−1) すなわち 1024(2n−1)
|
各々の棒のnのとりうる値は立てた本数を限度とする。
すなわち1/16cm棒は、1024本だから、1024×2ー1=2047 で、
最後の1/16棒は、2047番目です。64cm棒だと1本だから1024番目
ところで立てた棒は完全に左右(?)対象的に並んでいるので、AからでもBからでも同じ順番で並んでいる。
そして問3の2000番目ですが、各々の棒のn番目を求める式にイコール2000とおいて正の
整数解が得られるものがそれです。
すなわち 16(2n−1)=2000でn=63となるから、2000番目は、64本立っている
1cm棒の63本目です。
答え 1cm棒
因みに左から2000番目は(総数2047の)右から48番目だから、
16(2n−1)=48で、n=2となって左からの63本目と合致する。

解答・その9
(ペンネ−ム:kiyo)
問1.
64cmの棒を(1/4)cmづつに分割することになるから、
64÷(1/4)=256
256本。
問2.
| 1 | 2 | 3 | 4
| 5 | 6 | 7 | 8
| 9 | 10 | 11
|
| 64 | 32 | 16 | 8
| 4 | 2 | 1 | 1/2
| 1/4 | 1/8 | 1/16
|
64cmの棒を11本立てたことに等しいから、
64×11=704
704cm。
問3.
立てた棒の総本数は、
(64÷(1/16))×2-1=2047(本)
左のAの棒から1番と番号をつけていくとBの棒は2049番となる。
Aの方から2000番目の棒は2001番の棒に相当する。
64cmの棒は、(2049+1)÷2=1025(番)
B側の32cmの棒は、(2049+1025)÷2=1537(番)
Bに近い16cmの棒は、(2049+1537)÷2=1793(番)
Bに近い8cmの棒は、(2049+1793)÷2=1921(番)
Bに近い4cmの棒は、(2049+1921)÷2=1985(番)
Bに近い2cmの棒は、(2049+1985)÷2=2017(番)
(1985+2017)÷2=2001(番)
この棒の長さは1cmとなる。
1cm。
2001年の問題らしいですね。

解答・その10
(ペンネ−ム:巷の夢)
題意から条件を整理すると、2の累乗がポイントですので、
以下の表のようにまとめられる。
| NO. | 棒の長さ | 本数 | AB間の間隔をLとした時の棒の立つ間隔の分母数
|
|---|
| 1 | 26 | 20 | 21=2
|
| 2 | 25 | 21 | 22=4
|
| 3 | 24 | 22 | 23=8
|
| 4 | 23 | 23 | 24=16
|
| 5 | 22 | 24 | 25=32
|
| 6 | 21 | 25 | 26=64
|
| 7 | 20 | 26 | 27=128
|
| 8 | 2-1 | 27 | 28=256
|
| 9 | 2-2 | 28 | 29=512
|
| 10 | 2-3 | 29 | 210=1024
|
| 11 | 2-4 | 210 | 211=2048
|
この表から、
問1. 長さ1/4はNO.9であるから本数は 28=256本となる。
問2. 求めるものは、棒の長さ×本数であるから、26×11=704cmとなる。
問3. 2000番ということは2000/2048=125/128=125/27 である。
分母が 27であるから、棒の長さは 20=1である。

解答・その11
(ペンネ−ム:水の流れ)
1.64cmが1本、32cmが2本、16cmが4本 、
・・・で長さと棒の本数の積が一定の64に気がつく。
よって、1/4cmのときの棒の本数をx本とすると、(1/4)x=64
したがって、x=256 答 256本
2.この作業は最初、長さが64cm棒が何本かあって、1回の作業で1本づつ必要です。
よって、(1/16)cmの長さになるまで、11回の作業になります。
したがって、長さが64cm棒が11本使用されたから、11×64=704(cm)
3.(1/16)cmの長さの棒を立て終わったときを考えます。
奇数番目がすべて、(1/16)cmの長さの棒です。
このことに着目して、2000番目は偶数だから、(1/16)cm 以外の棒
2000÷2=1000 より、偶数番目だから、(1/8)cm 以外の棒
次に、1000÷2=500 より、偶数番目だから、(1/4)cm 以外の棒
また、500÷2=250 より、偶数番目だから、(1/2)cm 以外の棒
さらに、250÷2=125 より、奇数番目だから、1cm の棒 となる。
したがって、2で割って、順に奇数番目の棒を取り除いて作業を反対に
考えてたのです。
* 2000の2進法の表し方と関係しているみたい。

解答・その12
(ペンネ−ム:BossF)
問い1 どの長さの棒も、長さの合計は64cmですから
64÷(1/4)=256本…答
問い2 1本の長さは 26〜2-4 の11通りですから
64x11=704cm…答
2n cm の棒を<n>とあらわし
Aからn番目を、便宜的にn+1号といいかえます
すると目標の2000番目は2001号です
さて、2001号までの<-4>は、全ての偶数号にあり、これを全部抜くと
2001÷2=1000…1 ですから、2001号は1001号にかわります。
この時、1001号までの<-3>も、全ての偶数号にあり、これを全部抜くと
1001÷2=500…1 ですから、1001号は501号にかわります。
以下同様の手順を繰り返すと
<-2>を抜く⇒ 501号→251号
<-1>を抜く⇒ 251号→126号
ここで、「元の2001号」が偶数号に変わりました
すなわち、2000番目は20=1cm です。 …答

解答・その13
(ペンネ−ム:夜ふかしのつらいおじさん)
次のような表を作ります。棒の長さは、ステップが進むごとに半分になりま
す。棒を1本立てるごとにその棒の左右(つまり2カ所)に新たに棒を立てるス
ペースができます。ですから棒の本数は2倍になっていきます。
| 番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
|
|---|
| 棒の長さL | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 1/2 | 1/4 | 1/8 | 1/16
|
|---|
| 棒の本数n | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024
|
|---|
| L×n | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64
|
|---|
| 棒の本数の累計 | 1 | 3 | 7 | 15 | 31 | 63 | 127 | 255 | 511 | 1023 | 2047
|
|---|
(棒の本数はA、B以外に立てたもの)
問1 (1/4)cmの棒は、表より256本
問2 64×11=704cm
問3
棒の本数の累計を見ると、2000番目は11番目のステップで棒を立てて
はじめてできます。さて、次のように1回ステップが進むと棒の通し番号がどう
変わるかを考えます。すると、新しく棒を立てたことで今まで立っていた棒の通
し番号は偶数、新しく立てた棒の通し番号は奇数になります。2000は偶数な
ので今までにすでに立っていた棒です。
| 今まで立ってる棒の通し番号 | 0 | | 1 | | 2 | | 3 | ・・・
|
|---|
| 今まで立ってる棒 | A | | | | | | | | | | ・・・
|
|---|
| 新たに立てる棒 | | ^ | | ^ | | ^ | | ・・・
|
|---|
| 新しい棒の通し番号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ・・・
|
|---|
2000を2で割る作業を繰り返すと、4回目で奇数になります。
2000→1000→500→250→125
これは11番目のステップから見て4回前のステップで新しく立てられた棒であ
るということです。ですから7回目のステップで立てた棒は、1cmの棒です。

解答・その14
(ペンネ−ム:teki)
1) 256本
2) 704cm
3) 1cm
<解法>
要するに2の累乗の問題ですね。
1は、26から2-2までの段階が9段階あるので、
29-1=28で256本となります。
2は、各段階の長さと本数を掛ければ、全て64になるので、合計11段階の
長さの合計は、64×11=704cmとなります。
3が少々複雑ですが、Aから2000本目ということは、対称性から、Bから
48本目ですので、それぞれの長さの棒が立っている位置の法則が以下のように
なることから、計算できます。
| 1/16 | 2n+1番目
|
| 1/8 | 4n+2番目
|
| 1/4 | 8n+4番目
|
| 1/2 | 16n+8番目
|
| 1 | 32n+16番目
|
| 2 | 64n+32番目
|
| 4 | 128n+64番目
|
| 8 | 256n+128番目
|
| 16 | 512n+256番目
|
| 32 | 1024n+512番目
|
| 64 | 1024番目
|
Aからn番目の棒の長さとnの関係は次のようになります。
nを2で割っていって、m回割り切れる場合の棒の高さは、2m×1/16
これを2000に適用すると、m=4となるので、2000番目の棒の長さは
24×1/16=1
要するにnを素因数分解したときに出てくる2の個数によって棒の長さが
決まるということですね。

解答・その15
(ペンネ−ム:kirkland)
問1
棒の長さが半分になると、本数が2倍になるので、
(棒の長さ)×(その長さの棒の本数)は64cmで一定。
というわけで、64÷(1/4)=256本
問2
棒の長さは64cm、32cm、……、(1/16)cmの11種類あるので、
長さの総和は64×11=704cm
問3
2000を2進数で表すと11111010000(2)で、下から5桁目に初めて1が現れる。
これは左から2000本目の棒が5番目に短い棒であることを表しています。
というわけで、長さは1cm

解答・その16
(ペンネ−ム:高橋 道広)
解答
問1 256本
問2 704cm
問3 1/2cm
解説
問1
ある長さの棒を立てると区間は前回の2倍になり、棒の本数も2倍
必要になる。しかし棒の長さは半分になるので加える棒の長さの総
和は変わらない。
64cm 1本 計64cm
32cm 2本 計64cm
1/4cm 64÷1/4=256本となります。
問2
長さが64=26から1/16=2-4まで6-(-4)+1
11種類で上に書いたことから総和は11×64=704cm
問3
64cmはABを2等分 32cmはABを4等分 ...1/16はABを128÷1/16=
2048等分するのでAに0 Bに2048 その間の棒に1から順に番号を付け
ると、2進法で10000000000のところに64cm 1000000000 11000000000
のところに32cm...という風に棒を立てると考えられます。
このようにして最後は 1 11 101 111...のところに1/16の棒を立
てることになります。 つまり下の位から数えて初めて1が出るところを
考え1なら1/16 10なら1/8 100なら1/4...の棒を立てるのですから
2000を2進法で表すとよいのです。でも面倒なので 2048-2000=48を
2進法で表します。左右対称ですから同じ長さの棒を立てることになりま
すからね。で 48=32+16=110000(2進法)ですから 1cmの棒が立っ
てるはずです。

解答・その17
(ペンネ−ム:浜田 明巳)
(1) 256本
(2) 704cm
(3) 1cm
Excelのマクロ
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Dim kotae1 As Long
Dim kotae20 As Long
Dim kotae21 As Long
Dim kotae30 As Long
Dim kotae31 As Long
Dim bunshi As Integer
Dim bumbo As Integer
Dim a(10000, 1) As Integer
Dim b(10000, 1) As Integer
Dim bounokazu As Long
Dim owari As Integer
Dim gcd As Long
Dim j As Long
'
bunshi = 64
bumbo = 1
bounokazu = 1
a(1, 0) = 64
a(1, 1) = 1
While bumbo < 16
If bunshi > 1 Then
bunshi = bunshi / 2
Else
bumbo = bumbo * 2
End If
For j = 1 To 2 * bounokazu + 1
If j Mod 2 Then
b(j, 0) = bunshi
b(j, 1) = bumbo
Else
b(j, 0) = a(j / 2, 0)
b(j, 1) = a(j / 2, 1)
End If
Next j
bounokazu = 2 * bounokazu + 1
For j = 1 To bounokazu
a(j, 0) = b(j, 0)
a(j, 1) = b(j, 1)
Next j
Wend
'
kotae1 = 0
kotae20 = 0
kotae21 = 1
For j = 1 To bounokazu
Range("A" & j).Select
Cells(j, 1).Value = a(j, 0)
Cells(j, 2).Value = a(j, 1)
If a(j, 0) = 1 And a(j, 1) = 4 Then
kotae1 = kotae1 + 1
End If
'wa=kotae20/kotae21+a(j,0)/a(j,1)
' =(kotae20*a(j,1)+kotae21*a(j,0))/(kotae21*a(j,1))
kotae20 = kotae20 * a(j, 1) + kotae21 * a(j, 0)
kotae21 = kotae21 * a(j, 1)
gcd = GCM(kotae20, kotae21)
kotae20 = kotae20 / gcd
kotae21 = kotae21 / gcd
Next j
kotae30 = a(2000, 0)
kotae31 = a(2000, 1)
'
Range("D1").Select
Cells(1, 4).Value = kotae1
Cells(2, 4).Value = kotae20
If kotae21 > 1 Then
Cells(2, 5).Value = kotae21
End If
Cells(3, 4).Value = kotae30
If kotae31 > 1 Then
Cells(3, 5).Value = kotae31
End If
End Sub
Private Function GCM(ByVal a As Long, ByVal b As Long) As Long
If b = 0 Then
GCM = a
Else
GCM = GCM(b, a Mod b)
End If
End Function

正解者

まとめ
規則性があるのはわかっているのですが、それをすっきりした形に抽象化するのは
むずかしいという問題ですね。
全体の様子は、何人かの方がわかりやすく表にしてくださったので、それを見ていただければいいかと思います。
例えば勝浦捨てる造さんの表を使わせていただくと、
2cmの棒は32本あって、10番目の2cm棒は全体としては608番目だというように
出せますね。
しかしながら、逆に3番の問題のように2000番目は? と聞かれると、表と式を頼りに探さなければなりません。
ストレートに2000番目を探すにはどうしたらいいでしょうか。
高橋 道広さん、kirklandさんの解答にありますように
2進法表記に直し、下からたどって最初に1となる桁を探すのです。
(1/16)cm棒のいる場所は、1,3,5,・・・,(2n−1)ですが、これらの数を2進数
表記に直すと、必ず最初の桁は1になります。
(1/8)cm棒のいる場所は、2,6,10,・・・,2(2n−1)ですが、これらの数を2進数
表記に直すと、必ず最初の桁は0、次は1になります。
以下同様ですね。
「2進法」ということばを使わないにしても、
アイディアはかなりそれに近い方もいらっしゃいます。
いずれにしても規則性をひとつの形にまとめるのは、むずかしいことだと思いますが、
結果を知るとその美しさに驚かされますね。

 E-mail
E-mail
 戻る
戻る
 top
top





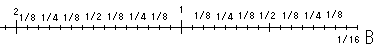
 E-mail
E-mail
 戻る
戻る
 top
top