Weekend Mathematics乛栤戣乛栤戣66
俇俇丏偍偼偠偒偺暲傋曽
愒丄敀丄惵偺偍偼偠偒偑偦傟偧傟偵偨偔偝傫偁偭偰丄嵍偐傜弴偵侾楍偵暲傋偰偄偒傑偡丅 偨偩偟丄愒偺師偼昁偢敀丄敀偺師偼昁偢惵傪暲傋傞傕偺偲偟傑偡丅
- 係屄暲傋傞暲傋曽偼壗捠傝偁傝傑偡偐丠
- 俋屄暲傋偨偲偒丄嵍偼偟傕塃偼偟傕愒偵側傞暲傋曽偼壗捠傝偁傝傑偡偐丠
僺乕僞乕愭惗偲拞妛擖帋偺嶼悢偵挧愴両
僺乕僞乕丒僼儔儞僋儖
怴挭幮
恄屗彈妛堾拞摍晹2001擭搙擖帋
乮儁儞僱亅儉丗傗側偣乯
栤偄侾偺摎偊偼侾俈捠傝偱偡丅
慻傒崌傢偣偼
愒敀惵惵丄愒敀惵敀丄愒敀惵愒丄敀惵惵惵丄敀惵惵敀丄敀惵惵愒丄敀惵愒敀丄敀惵敀惵
惵惵惵惵丄惵惵惵敀丄惵惵惵愒丄惵惵敀惵丄惵惵愒敀丄惵敀惵惵丄惵敀惵敀丄惵敀惵愒
惵愒敀惵丄偱偟偨丒丒偼偀偼偀乣偮偐傟偨傃偂乣乣

乮儁儞僱亅儉丗僗僠儏乕僨儞僩乯
愒傪抲偄偨応崌丄師偼敀丄偦偺師偼惵偲側傞偺偱丄乮愒仺敀仺惵乯乧嘆偲側傞丅
敀傪抲偄偨応崌丄師偼惵偲側傞偺偱丄乮敀仺惵乯乧嘇偲側傞丅
惵偺応崌丄惂尷偼側偄偺偱乮惵乯乧嘊
嘆乣嘊偺暲傋曽偑壗捠傝偐挷傋傟偽傛偄偺偱丄嘆乣嘊偱丄屄悢偑俁丆俀丆侾偲堘偆偙
偲偵拲栚偟偰丄栤戣傪夝偔丅
俀丆俋屄暲傋偰丄椉抂偑愒丅
傑偢丄愒仺敀仺惵仺丒丒丒丒丒丒仺愒偼妋掕丅
傛偭偰娫偵偁傞俆偮偺暲傋曽傪峫偊傟偽傛偄丅
俆亖侾亄侾亄侾亄侾亄侾
俆亖侾亄侾亄侾亄俀
俆亖侾亄侾亄俁
俆亖侾亄俀亄俀
俆亖俀亄俁
傛偭偰
| 侾亄係両乛俁両侾両亄俁両乛俀両侾両亄俁両乛侾両俀両亄俀両 | |
| 亖 | 侾亄係亄俁亄俁亄俀 |
| 亖 | 侾俁 |

乮儁儞僱亅儉丗彑塝幪偰傞憿乯
栤偄乮侾乯
愒偑嵍抂偺応崌丂戣堄傛傝丂愒敀惵偲側偭偰塃抂偼愒敀惵偳傟偱傕俷俲偱丂3庬椶
敀偑嵍抂偩偲師偼惵偱妋掕偟偰丂丂敀惵偺師偑愒偩偲師偼敀偩偗偱丂1庬椶
敀惵偺師偑敀偩偲師偼昁偢惵偱丂1庬椶
敀惵偺師偑惵偩偲師偼偳傟偱傕俷俲偱丂3庬椶
惵偑嵍抂偩偲嵍偐傜2斣栚偵偼愒敀惵偳傟傕俷俲
偦偙偱傑偢愒偩偲昁偢敀惵偲側偭偰惵愒敀惵偺1庬椶
嵍抂偑惵偱師偵敀傪抲偔偲3斣栚偼昁偢惵偱惵敀惵偲側偭偰塃抂偵偼愒敀惵偳傟偱傕俷俲偱丂3庬椶
師偵嵍偐傜惵惵偲暲傋偨偲偒3斣栚偵愒傪抲偔偲師偼敀偩偗偱丂1庬椶
3斣栚偑敀偩偲師偼昁偢惵偱1庬椶
師偵嵍偐傜惵惵惵偲暲傋偨傜塃抂偼愒敀惵偳傟傕俷俲偱3庬椶
偱丄慡晹懌偟偰丂侾俈庬椶偱偡丅
栤偄乮俀乯
(嘆)愒(2)敀(嘊)惵丂丂丂(9)愒丂偼妋掕
偲偙傠偱乮俋乯偑愒側傜乮俉乯偼昁偢惵偵側傞偺偱丂巆傝乮係乯偐傜乮俈乯傪寛傔傞
乮係乯偑愒側傜乮係乯乮俆乯乮俇乯偼愒敀惵偱乮俈乯偵偼敀偐惵偱2庬椶
乮係乯敀側傜乮係乯乮俆乯偼敀惵偱乮俇乯乮俈乯偵偼丂敀惵丄惵惵丄惵敀丄愒敀偺係庬椶
師偵乮係)惵偺応崌偺乮俆乯乮俇乯乮俈乯偵偼丂丂愒敀惵丄敀惵敀丄敀惵惵丄惵惵惵丄惵敀惵丄惵愒敀丄惵惵敀偺7庬椶偲側偭偰
崌寁偟偰侾俁庬椶偱偡丅丂丂丂丂丂丂

乮儁儞僱亅儉丗儌儖儌僢僩戝恇乯
1) 4屄暲傋傞曽朄
| 愒仺敀 仺惵 仺愒丄敀丄惵----- | 3捠傝 |
| 敀仺惵 仺愒 仺敀------------- | 1捠傝 |
| 敀仺惵 仺敀 仺惵------------- | 1捠傝 |
| 敀仺惵 仺惵 仺愒丄敀丄惵----- | 3捠傝 |
| 惵仺愒 仺敀 仺惵------------- | 1捠傝 |
| 惵仺敀 仺惵 仺愒丄敀丄惵----- | 3捠傝 |
| 惵仺惵 仺愒 仺敀------------- | 1捠傝 |
| 惵仺惵 仺敀 仺惵------------- | 1捠傝 |
| 惵仺惵 仺惵 仺愒丄敀丄惵----- | 3捠傝 |
2) 嵍抂偲塃抂偵愒傪暲傋丄慡懱偱9屄暲傋傞曽朄
嵟弶偺嵍抂偐傜3屄偼愒仺敀 仺惵偱嵟屻偺塃抂偺愒偺1屄慜偼昁偢惵偱偁傝偝傜偵偦
偺惵偺慜偼惵偐敀偱偁傞偙偲偵拝栚偡傞偲4屄偺暲傋曽傪峫偊傟偽傛偄丅
| 愒仺敀 仺惵 仺敀丄惵--------- | 2捠傝 |
| 敀仺惵 仺愒 仺敀------------- | 1捠傝 |
| 敀仺惵 仺敀 仺惵------------- | 1捠傝 |
| 敀仺惵 仺惵 仺敀丄惵--------- | 2捠傝 |
| 惵仺愒 仺敀 仺惵------------- | 1捠傝 |
| 惵仺敀 仺惵 仺敀丄惵--------- | 2捠傝 |
| 惵仺惵 仺愒 仺敀------------- | 1捠傝 |
| 惵仺惵 仺敀 仺惵------------- | 1捠傝 |
| 惵仺惵 仺惵 仺敀丄惵--------- | 2捠傝 |
摎 (1) 17捠傝丄(2) 13捠傝
崱屻偲傕傛傠偟偔偍婅偄偄偨偟傑偡丅

乮儁儞僱亅儉丗僪儔乯
乮乬仜偮栚乭偲偄偆昞尰偼偡傋偰嵍抂偐傜悢偊偨傕偺偲偡傞乯
侾丆
乮鶣乯嵍抂偑愒偺帪丂丂丂丂丂愒丆敀丆惵丆仜
丂丂係偮栚偵偼丄愒傑偨偼敀傑偨偼惵偺偳偺怓偱傕擖傟傞偺偱丄俁捠傝丅
乮鶤乯嵍抂偑敀偺帪丂丂丂丂丂敀丆惵丆仜丆仜
丂丂俁偮栚偵丄愒傑偨偼敀偑擖傞偲丄係偮栚傕寛掕偟丄俀捠傝丅
丂丂俁偮栚偵丄惵偑擖傞偲丄係偮栚偵偼丄愒傑偨偼敀傑偨偼惵偺偳偺怓偱傕擖傟傞偺偱丄俁捠傝丅
丂丂崌傢偣偰俆捠傝丅
乮鶥乯嵍抂偑惵偺帪丂丂丂丂丂惵丆仜丆仜丆仜
丂丂俀偮栚偵愒偑擖傞偲丄俁偮栚丒係偮栚傕寛傑傝丄侾捠傝丅
丂丂俀偮栚偵敀偑擖傞偲丄俁偮栚偼惵偵側傝丄
丂丂係偮栚偵偼丄愒傑偨偼敀傑偨偼惵偺偳偺怓偱傕擖傟傞偺偱丄俁捠傝丅
丂丂俀偮栚偵惵偑擖傝丄
丂丂俁偮栚偵丄愒傑偨偼敀偑擖傞偲丄係偮栚傕寛掕偟丄俀捠傝丅
丂丂俁偮栚偵丄惵偑擖傞偲丄係偮栚偵偼丄
丂丂愒丒敀丒惵偺偳偺怓偱傕擖傟傞偺偱丄俁捠傝丅
丂丂崌傢偣偰俋捠傝丅
乮鶣乯乮鶤乯乮鶥乯傛傝丄侾俈捠傝丅
俀丆
栤戣傛傝丄嵍抂偲塃抂偼愒偵寛掕丅
愒丆仜丆仜丆仜丆仜丆仜丆仜丆仜丆愒
師偵丄嵍抂偑愒偱偁傞偙偲傛傝丄俁偮栚傑偱偼寛掕偡傞丅
愒丆敀丆惵丆仜丆仜丆仜丆仜丆仜丆愒
俋偮栚偑愒偱偁傞偙偲傛傝丄俉偮栚偼惵偱偁傞昁梫偑偁傞丅
愒丆敀丆惵丆仜丆仜丆仜丆仜丆惵丆愒
偙偙傑偱偼栤戣傛傝寛掕偝傟傞丅
俉偮栚偑惵偱偁傞偙偲傛傝丄俈偮栚偼敀傑偨偼惵偱側偔偰偼側傜側偄丅
係偮栚丄俆偮栚丄俇偮栚偵娭偟偰偼丄尰帪揰偱摿偵惂尷偼柍偄丅
傛偭偰丄偙偺栤戣偺摎偊偼
乬係屄暲傋偨帪丄塃抂偑敀傑偨偼惵偵側傞暲傃曽偼壗捠傝偁傝傑偡偐丠乭
偲偄偆栤戣偺摎偊偲堦抳偡傞丅
偩偐傜丄乬係屄暲傋偨帪丄塃抂偑敀傑偨偼惵偵側傞暲傃曽偼壗捠傝偁傝傑偡偐丠乭
偲偄偆栤戣偺摎偊傪峫偊傞偙偲偵偡傞丅
乮鶣乯嵍抂偑愒偺帪丂丂丂丂丂愒丆敀丆惵丆仜
丂丂係偮栚偵偼丄敀傑偨偼惵偑擖傞偺偱丄俀捠傝丅
乮鶤乯嵍抂偑敀偺帪丂丂丂丂丂敀丆惵丆仜丆仜
丂丂俁偮栚偵丄愒傑偨偼敀偑擖傞偲丄係偮栚傕寛掕偟丄俀捠傝丅
丂丂俁偮栚偵丄惵偑擖傞偲丄係偮栚偵偼丄敀傑偨偼惵偑擖傞偺偱丄俀捠傝丅
丂丂崌傢偣偰係捠傝丅
乮鶥乯嵍抂偑惵偺帪丂丂丂丂丂惵丆仜丆仜丆仜
丂丂俀偮栚偵愒偑擖傞偲丄俁偮栚丒係偮栚傕寛傑傝丄侾捠傝丅
丂丂俀偮栚偵敀偑擖傞偲丄俁偮栚偼惵偵側傝丄
丂丂係偮栚偵偼丄敀傑偨偼惵偑擖傞偺偱丄俀捠傝丅
丂丂俀偮栚偵惵偑擖傝丄
丂丂俁偮栚偵丄愒傑偨偼敀偑擖傞偲丄係偮栚傕寛掕偟丄俀捠傝丅
丂丂俁偮栚偵丄惵偑擖傞偲丄係偮栚偵偼丄敀傑偨偼惵偑擖傞偺偱丄俀捠傝丅
丂丂崌傢偣偰俈捠傝丅
乮鶣乯乮鶤乯乮鶥乯傛傝丄侾俁捠傝丅

乮儁儞僱亅儉丗僗儌乕僋儅儞乯
1丄11乯嵟弶丄愒側傜丄嵟屻偺4屄栚偑丄3捠傝丅丗3
丂丂12乯敀側傜丄3屄栚偑丄愒偺帪丅丗1
丂丂丂丂丂丂丂丂丂丂丂丂丂敀偺帪丅丗1
丂丂123乯惵偺帪丄4屄栚偑3捠傝丅丗3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂寁丗5
丂丂13乯惵偺帪丄2屄栚偑愒偺帪丅丗1
丂丂丂丂敀偺帪丄4屄栚偑3捠傝丅丗3
丂丂丂丂惵偺帪丄12)捠傝丅丗5
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂寁丗9
埲忋偐傜丄3+5+9=17捠傝丅
2丄嵟弶偑愒偱丄嵟屻傕愒偲偄偆偙偲偼丄
嵟屻偐傜2斣栚偼惵偩偐傜丄4乣7屄栚傑偱偺怓傪峫偊傟偽傛偄丅
4屄栚偑愒側傜丄7屄栚偼丄惵偱傕敀偱傕椙偄丅丗2
丂丂丂丂敀側傜丄6-7屄栚偼丄愒-敀丄敀-惵丄惵-敀丄惵-惵偺偄偢傟偱傕傛偄丅丗4
丂丂丂 惵側傜丄5屄栚偼丄愒偱丄丗1
丂丂丂丂敀偱丄7屄栚偑敀偱傕惵偱傕椙偄偺偱丄丗2
丂丂丂丂惵偱丄6屄栚偼丄愒偱丄丗1
丂丂丂丂丂丂丂丂丂丂丂丂敀偱丄丗1
丂丂丂丂丂丂丂丂丂丂丂丂惵偱丄7屄栚偼敀偱傕惵偱傕椙偄偺偱丄丗2
崌寁丗2+4+1+2+1+1+2=13捠傝丅

乮儁儞僱亅儉丗昹揷丂柧枻乯
偄偮傕偺傛偆偵丆俤倃俠俤俴偺儅僋儘偱夝偒傑偟偨丏僨乕僞張棟偼丆傗偼傝俤倃俠俤俴偱偡丏
愒丆敀丆惵傪偦傟偧傟侽丆侾丆俀偲偟丆侽偺師偼侾丆侾偺師偼俀偲偟傑偡丏
栤戣侾偱偼係屄偺偍偼偠偒偺暲傃曽丆栤戣俀偱偼俋屄偺偍偼偠偒偺暲傃曽偺憤悢傪媮傔傑偡丏
偨偩偟丆栤戣俀偱偼丆嵟弶偲嵟屻偼侽偲偟傑偡丏
偙偺儅僋儘偵傛傝丆摎偼丆
丂丂栤戣侾丂侾俈捠傝
丂丂栤戣俀丂侾俁捠傝
偲側傝傑偡丏
偙偺栤戣傪堦斒壔偟偨傝丆悢妛揑偵尒偰丆棤懁偵偳傫側棟榑偑愽傫偱偄傞偐丆
偲峫偊傞偺偼丆嬯庤側偺偱丆偙偺偔傜偄偵偟偰偍偒傑偡丏
17
| 愒 敀 惵 愒 |
| 愒 敀 惵 敀 |
| 愒 敀 惵 惵 |
| 敀 惵 愒 敀 |
| 敀 惵 敀 惵 |
| 敀 惵 惵 愒 |
| 敀 惵 惵 敀 |
| 敀 惵 惵 惵 |
| 惵 愒 敀 惵 |
| 惵 敀 惵 愒 |
| 惵 敀 惵 敀 |
| 惵 敀 惵 惵 |
| 惵 惵 愒 敀 |
| 惵 惵 敀 惵 |
| 惵 惵 惵 愒 |
| 惵 惵 惵 敀 |
| 惵 惵 惵 惵 |
13
| 愒 敀 惵 愒 敀 惵 敀 惵 愒 |
| 愒 敀 惵 愒 敀 惵 惵 惵 愒 |
| 愒 敀 惵 敀 惵 愒 敀 惵 愒 |
| 愒 敀 惵 敀 惵 敀 惵 惵 愒 |
| 愒 敀 惵 敀 惵 惵 敀 惵 愒 |
| 愒 敀 惵 敀 惵 惵 惵 惵 愒 |
| 愒 敀 惵 惵 愒 敀 惵 惵 愒 |
| 愒 敀 惵 惵 敀 惵 敀 惵 愒 |
| 愒 敀 惵 惵 敀 惵 惵 惵 愒 |
| 愒 敀 惵 惵 惵 愒 敀 惵 愒 |
| 愒 敀 惵 惵 惵 敀 惵 惵 愒 |
| 愒 敀 惵 惵 惵 惵 敀 惵 愒 |
| 愒 敀 惵 惵 惵 惵 惵 惵 愒 |
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Dim a(4) As Integer
Cells(1, 1).Value = 0
Range("A1").Select
Call check1(1, a())
End Sub
Sub check1(ByVal n As Integer, ByRef a() As Integer)
Dim a_max As Integer
Dim j As Integer
If n > 1 And a(n - 1) < 2 Then
a(n) = a(n - 1) + 1
a_max = a(n - 1) + 1
Else
a(n) = 0
a_max = 2
End If
While a(n) <= a_max
If n < 4 Then
Call check1(n + 1, a())
Else
Cells(1, 1).Value = Cells(1, 1).Value + 1
For j = 1 To 4
Cells(Cells(1, 1).Value, j + 1).Value = ohajiki(a(j))
Next j
End If
a(n) = a(n) + 1
Wend
End Sub
Private Function ohajiki(ByVal n As Integer) As String
Select Case n
Case 0
ohajiki = "愒"
Case 1
ohajiki = "敀"
Case Else
ohajiki = "惵"
End Select
End Function
Sub Macro2()
Sheets("Sheet2").Select
Dim a(9) As Integer
Cells(1, 1).Value = 0
Range("A1").Select
a(1) = 0
a(9) = 0
Call check2(2, a())
End Sub
Sub check2(ByVal n As Integer, ByRef a() As Integer)
Dim a_max As Integer
Dim j As Integer
If a(n - 1) < 2 Then
a(n) = a(n - 1) + 1
a_max = a(n - 1) + 1
Else
a(n) = 0
a_max = 2
End If
While a(n) <= a_max
If n < 8 Then
Call check2(n + 1, a())
ElseIf a(8) = 2 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
For j = 1 To 9
Cells(Cells(1, 1).Value, j + 1).Value = ohajiki(a(j))
Next j
End If
a(n) = a(n) + 1
Wend
End Sub

乮儁儞僱亅儉丗奰杮丂峗乯
栤戣侾丗係屄偺暲傋曽
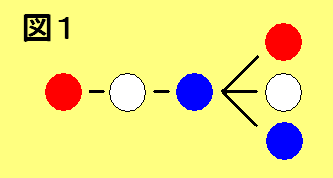 仠嵍抂偑愒偺応崌乮恾侾乯
仠嵍抂偑愒偺応崌乮恾侾乯
愒仺敀仺惵偱俁屄栚傑偱妋掕丅
係屄栚偼帺桼偵慖傋傞丂丒丒丒丂俁捠傝
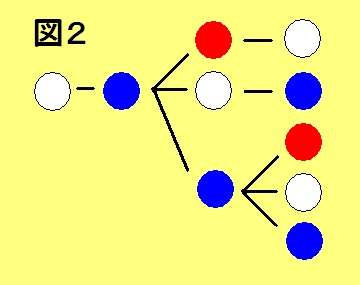 仠嵍抂偑敀偺応崌乮恾俀乯
仠嵍抂偑敀偺応崌乮恾俀乯
敀仺惵偱俀屄栚傑偱妋掕丅
俁屄栚偵愒丒敀傪慖傇偲係屄栚傕堦堄偵妋掕丅
俁屄栚偵惵傪慖傇偲丄係屄栚傕帺桼偵慖傋傞丅丂丒丒丒丂俆捠傝
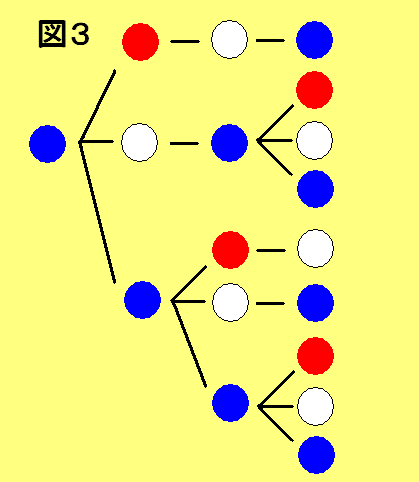 仠嵍抂偑惵偺応崌乮恾俁乯
仠嵍抂偑惵偺応崌乮恾俁乯
俀屄栚偑帺桼偵慖傋丄俀屄栚偵愒傪慖傇偲係屄栚傑偱妋掕丅
俀屄栚偵敀傪慖傇偲俁屄栚偺惵偑妋掕偟丄係屄栚偼帺桼偵慖傋傞丅
俀屄栚偵惵傪慖傇偲俁屄栚傕帺桼偵慖傋丄俁屄栚偵愒丒敀傪慖傇偲係屄栚傕堦堄偵
妋掕丅
俁屄栚偵惵傪慖傇偲係屄栚傕帺桼偵慖傋傞丅丂丒丒丒丂俋捠傝
傛偭偰崌寁偱侾俈捠傝偲側傞丅
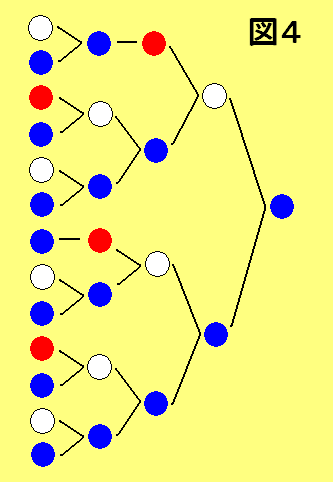 栤戣俀丗椉抂偑愒偵側傞俋屄偺暲傋曽
栤戣俀丗椉抂偑愒偵側傞俋屄偺暲傋曽
侾偮慜乮嵍懁乯偵偁傞怓偺僷僞乕儞傪峫偊偰傒傞偲
乮仜丗暲傋傜傟傞丂亊丗暲傋傜傟側偄乯
丒愒仺愒丗亊丂敀仺愒丗亊丂惵仺愒丗仜丂仺丂愒偺慜偼昁偢惵
丒愒仺敀丗仜丂敀仺敀丗亊丂惵仺敀丗仜丂仺丂敀偺慜偼愒偐惵
丒愒仺惵丗亊丂敀仺惵丗仜丂惵仺惵丗仜丂仺丂惵偺慜偼敀偐惵
嵍抂偑愒丂仺丂侾乣俁屄栚偼愒仺敀仺惵偺侾捠傝偟偐側偄丅乮係屄栚偼帺桼偵慖傋
傞乯
塃抂偑愒丂仺丂愒偺慜偼昁偢惵側偺偱丄俉丒俋屄栚偼惵仺愒偺侾捠傝偟偐側偄丅
傛偭偰偙偺栤戣偼
乽俆屄乮係乣俉屄栚乯偺暲傋曽偱丄塃抂乮俉屄栚乯偑惵偵側傞暲傋曽偑壗捠傝偁傞
偐乿
偲偄偆宍偵抲偒姺偊傜傟傞丅
忋婰偵帵偟偨乽慜偺怓偺僷僞乕儞乿傪巊偭偰塃抂偐傜峫偊偰偄偔偲
恾係偑摼傜傟丄慡晹偱侾俁捠傝偩偲暘偐傞丅

乮儁儞僱亅儉丗僒僓儞儅僯傾乯
侾丄傑偢丄堦斣嵍偵壗怓傪抲偔偐峫偊傞丅
乮侾乯丄愒傪偍偄偨偲偒丅
弴偵丄敀丄惵偲懕偔丅堦斣塃抂偵偼丄愒丄惵丄敀偑暲傋傜傟傞丅傛偭偰丄俁捠傝丅
乮俀乯丄敀傪偍偄偨偲偒丅
丂
弴偵丄惵偲懕偔丅俁斣栚偵偼丄愒丄惵丄敀偑暲傋傜傟傞丅俁斣栚偑愒丄敀偺偲偒丄
栤戣暥偐傜丄愒偺応崌偼弴偵敀丅敀偺応崌偼丄弴偵惵偲暲傋傜傟傞丅乮俀捠傝乯
師偵丄惵偺応崌丄愒丄惵丄敀傪暲傋傜傟傞丅乮俁捠傝乯丂傛偭偰丄偁傢偣偰俆捠傝丅
乮俁乯丄惵傪偍偄偨偲偒丅
俀斣栚偵暲傋傜傟傞偺偼丄愒丄敀丄惵丅
傑偢丄愒傪暲傋偨偲偒丄敀丄惵偲懕偔丅乮侾捠傝乯
師偵丄敀傪暲傋偨応崌丄惵偲懕偔丅堦斣塃偵偼丄愒丄惵丄敀傪暲傋傜傟傞丅乮俁捠傝乯
嵟屻偵丄惵傪暲傋偨応崌丄俁斣栚偵丄愒丄惵丄敀偑暲傋傜傟傞丅
俁斣栚偵丄愒丄敀傪暲傋偨応崌丄弴偵丄愒偺応崌偼敀丄敀偺応崌偼惵偲懕偔丅乮俀捠傝乯
俁斣栚偵丄惵傪暲傋偨応崌丄堦斣塃抂偵丄惵丄愒丄敀傪暲傋傜傟傞丅乮俁捠傝乯
偩傜偩傜偲懕偄偨偑丄俋捠傝丅
乮侾乯丄乮俀乯丄乮俁乯傛傝丄偁傢偣偰侾俈捠傝丅
俀丄傑偢丄堦斣嵍抂偵愒傪抲偔丅偡傞偲丄弴偵丄敀丄惵偲懕偔丅偁偲丄偍偔偙偲偑偱
偒傞偍偼偠偒偼偁偲俇偮偱偁傞丅
偦偙偱丄侾斣偺栤戣偺丄係屄暲傋傞暲傋曽偵拲栚偡傞丅偙偙偱丄嵟屻偵愒偑抲偗側偄
応崌傪峫偊傞偲丄俈斣栚偵抲偔偍偼偠偒偺怓偑愒偱偼側偄丅乮俉斣栚敀丄俋斣栚惵偲
懕偔偐傜乯偮傑傝丄侾斣偺栤戣偱塃抂偵抲偔偍偼偠偒偺怓偑愒埲奜偺暲傋曽傪慖傋偽
傛偄丅
侾斣偺栤戣傛傝丄峫偊傜傟傞偺偼丄
乮愒丄敀丄惵丄敀乯乮愒丄敀丄惵丄惵乯乮敀丄惵丄愒丄敀乯乮敀丄惵丄敀丄惵乯
乮敀丄惵丄惵丄敀乯乮敀丄惵丄惵丄惵乯乮惵丄愒丄敀丄惵乯乮惵丄敀丄惵丄敀乯
乮惵丄敀丄惵丄惵乯乮惵丄惵丄敀丄惵乯乮惵丄惵丄愒丄敀乯乮惵丄惵丄惵丄敀乯
乮惵丄惵丄惵丄惵乯丂偺侾俁捠傝丅
俈斣栚偑敀丄惵偺偲偒丄俉斣栚丄惵丄塃抂偵愒傪抲偗偽傛偄丅
傛偭偰丄摎偊偼侾俁捠傝丅

乮儁儞僱亅儉丗俙俲乯
侾丏係偮暲傋傞丅
嵍抂偑愒偺偲偒丅
丂丂丂丂愒-敀-惵-俷丅丂3捠傝丅
嵍抂偑敀偺偲偒丅
丂丂丂丂敀-惵-俷-仠丅丂俷偑惵埲奜偱偼仠傕寛掕偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂俷偑惵偩偲仠偼3捠傝丅丂傛偭偰5捠傝丅
嵍抂偑惵偺偲偒丅
丂
丂丂丂丂惵-俷-仠-仢丅丂俷偑愒偱偼仠丒仢偑寛掕偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂俷偑敀偩偲仠偑寛掕偟丄仢偼3捠傝丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂俷偑惵偺応崌丄敀偑嵍抂偺帪偲摨堄側偺偱5捠傝丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂傛偭偰9捠傝丅
埲忋傛傝懌偟偰17捠傝丅
俀丏俋偮暲傋傞丅椉抂偑愒丅
忦審傛傝
愒-敀-惵-仜-仠-仢-仚-惵-愒傑偱寛掕偡傞丅
拞偺仜-仠-仢-仚偼忋偺4偮暲傋傞帪偲帡偰偄傞偑丄仚偑愒偩偲偄偗側偄偺偱
仚偑愒偵側傞帪偼仢偑惵偺帪丅
栤戣侾偐傜峫偊偰仚偑愒偵側傞偺偼4捠傝丅
17-4=13捠傝.

乮儁儞僱亅儉丗kiyo乯
愒丂侾丂敀丂俀丂惵丂俁丂偲偡傞丅
侾丏
俀丏侾俀俁仜仜仜仜俁侾丂偺宍偵側傜側偗傟偽側傜側偄丅
偟偨偑偭偰丄栤戣侾偵娨尦偝傟傞丅
偦偺側偐偱丄嵟屻偑乽侾乿仏偼晄揔偲側傞偺偱丄
侾俁捠傝丅

乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
侾丏師偺俈捠傝偑惓夝偩偲巚偄傑偡丅
愒敀惵惵丂敀惵敀惵丂敀惵惵惵丂惵愒敀惵丂惵敀惵惵丂惵惵敀惵丂惵惵惵惵
偟偐偟丄俀斣偺栤戣偺傛偆偵塃偼偟偑愒偺偙偲偑偁傞偲偄偆偙偲傪擣傔傞偺側傜師偺侾俈庬椶偱偡丅
乮偙偺拞偱塃偼偟偑愒傗敀偺傕偺偼偦偺塃偵敀傗惵偑偒偰偄傑偣傫丅
偙傟偼丄乽偨偩偟丄愒偺師偼昁偢敀丄敀偺師偼昁偢惵傪暲傋傞傕偺偲偟傑偡乿
偺儖乕儖偵斀偟偰偄傞偲巚偆偺偱偡偑丅乯
仠愒敀惵愒丂仜愒敀惵敀丂仜愒敀惵惵
仜敀惵愒敀丂仜敀惵敀惵丂仠敀惵惵愒丂仜敀惵惵敀丂仜敀惵惵惵
仜惵愒敀惵丂仠惵敀惵愒丂仜惵敀惵敀丂仜惵敀惵惵
仜惵惵愒敀丂仜惵惵敀惵丂仠惵惵惵愒丂仜惵惵惵敀丂仜惵惵惵惵
偙傟偼師偺侾偐傜係傑偱偺暲傃乮俁庬椶乯丄俀偐傜俆傑偱偺暲傃乮俆庬椶乯丄
俁偐傜俇傑偱偺暲傃乮俋庬椶乯偱偡丅
侾仺俀仺俁仺係仺俆仺俇
愒仺敀仺惵劍愒仺敀仺惵
丂丂丂丂丂劌敀仺惵劍愒
劆 劌敀
劆 劋惵
劋惵劍愒仺敀
劌敀仺惵
劋惵劍愒
劌敀
劋惵
俀丏摎偊偼侾俁庬椶偱偡丅
愒偱巒傑傞偲師偺敀丄偦偺師偺惵偲偼偠傔偺俁怓偑寛傑偭偰偟傑偄傑偡丅
傑偨丄塃偼偟偺愒偺慜偼惵偱側偗傟偽側傝傑偣傫丅
側偤側傜愒傗敀側傜師偵愒偑偙傜傟側偄偐傜偱偡丅
偍傢傝偺俀怓傕寛傑偭偰偟傑偄傑偡丅偮傑傝師偺傛偆側暲傃偵側傝傑偡丅
侾俀俁係俆俇俈俉俋 愒敀惵丒丒丒丒惵愒

乮儁儞僱亅儉丗偗傫偨傫乯
乮侾偺夝摎乯
係屄偺暲傋曽偼丄壓婰偺捠傝偱偁傞丅
| 愒仺敀仺惵仺愒 | 惵仺愒仺敀仺惵 |
| 愒仺敀仺惵仺敀 | 惵仺敀仺惵仺愒 |
| 愒仺敀仺惵仺惵 | 惵仺敀仺惵仺敀 |
| 敀仺惵仺愒仺敀 | 惵仺敀仺惵仺惵 |
| 敀仺惵仺敀仺惵 | 惵仺惵仺愒仺敀 |
| 敀仺惵仺惵仺愒 | 惵仺惵仺敀仺惵 |
| 敀仺惵仺惵仺敀 | 惵仺惵仺惵仺愒 |
| 敀仺惵仺惵仺惵 | 惵仺惵仺惵仺敀 |
| 惵仺惵仺惵仺惵 |
乮俀偺夝摎乯
戣堄偺俋屄偺暲傋曽傪壓偺傛偆偵昞偟偨丅
| 弴丂斣 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 |
|---|---|---|---|---|---|---|---|---|---|
| 偍偼偠偒偺怓 | 愒 | 敀 | 惵 | 惵 | 愒 |

乮儁儞僱亅儉丗teki乯
摎偊丂侾丂侾俈捠傝丂俀丂侾俁捠傝
亙夝朄亜
侾偼丄愒傪愭摢偵偟偨応崌俁捠傝丄敀傪愭摢偵偟偨応崌俆捠傝丄惵傪愭摢偵偟偨
応崌俋捠傝偺寁侾俈捠傝偱偡丅
俀偼丄嵟弶偲嵟屻偑愒偱偁傞偙偲偐傜丄俁屄栚傑偱偼丄愒敀惵偑妋掕偟傑偡丅
傑偨丄俉屄栚傕惵偱側偗傟偽側傝傑偣傫丅
係屄栚偐傜俈屄栚偺係偮偺暲傋曽偼丄侾傛傝侾俈捠傝偱偡偑丄俈屄栚偵偼愒偑偙
側偄偺偱丄侾俈捠傝偐傜嵟屻偑愒偵側傞係捠傝傪堷偄偰侾俁捠傝偲側傝傑偡丅
側偍丄偙偺忦審偱偺値屄偺偍偼偠偒偺暲傋曽偺悢傪俙乮値乯偲偡傞偲丄埲壓偺慟
壔幃偑惉棫偟傑偡丅
丂丂丂俙乮値乯亖俙乮値-1乯+俙乮値-2乯+俙乮値-3乯丂乮扐偟丄値亝俁偺帪丄俙乮値乯
亖俀値+1乯
偡側傢偪丄慜偺俁偮傪懌偟偨傕偺偑師偺悢偵側傞偲偄偆偙偲偱偡丅
偙偆偄偆悢楍傪僩儕儃僫僢僠悢楍偲偄偆傜偟偄偱偡偑丄弶帹偱偟偨丅乮僼傿儃僫
僢僠悢楍側傜暦偄偨偙偲偑偁傝傑偡丅僀僞儕傾偺悢妛幰偺柤慜傪偲偭偨悢楍偱丄栘偺巬暿
傟偺悢楍摍丄帺慠奅偵偼寢峔偁傞傛偆偱偡丅乯

乮儁儞僱亅儉丗kirkland乯
侾斣偺夝摎
係屄栚傑偱彂偗偽妋幚側偺偱偟傚偆偑丄柺搢側偺偱俁屄栚傑偱丅
乮愒偺忦審偑偁傞偺偱丄俁屄栚傑偱偼彂偐側偄偲僟儊乯
侾屄暲傋傞偲偒偼俁捠傝丄俀屄暲傋傞偲偒偼俆捠傝丄俁屄暲傋傞偲偒偼俋捠傝乮壓偺昞傛傝乯丅
| 侾屄栚 | 俀屄栚 | 俁屄栚 |
|---|---|---|
| 惵 | 惵 | 惵 |
| 敀 | ||
| 愒 | ||
| 敀 | 惵 | |
| 愒 | 敀 | |
| 敀 | 惵 | 惵 |
| 敀 | ||
| 愒 | ||
| 愒 | 敀 | 惵 |
俀斣偺夝摎
嵍抂乮侾屄栚乯偑愒偲偄偆偙偲偼丄俀屄栚偼敀丄俁屄栚偼惵偱丄係屄栚偐傜帺桼偵側傝傑偡丅
塃抂乮俋屄栚乯偑愒偲偄偆偙偲偼丄俉屄栚偼惵丄俈屄栚偼惵偐敀乮愒偱偼側偄乯丅
偲偄偆傢偗偱丄係屄栚偐傜俈屄栚傑偱偺係屄偩偗傪峫偊傑偡丅
係屄暲傋傞侾俈捠傝偺偆偪丄係屄栚偑愒乮俁屄栚偑惵乯偵側偭偰偟傑偆傕偺偑係捠傝偁傞偺偱丄
偙傟傪彍偔偲侾俁捠傝丅
彫妛惗偺朧偪傖傫丒偍忟偪傖傫丄幚嵺偺帋尡応偱偼丄係屄栚傑偱挷傋傑偟傚偆丅
偦偺曽偑妋幚偱偡傛両

乮儁儞僱亅儉丗崅嫶 摴峀乯
侾
n屄暲傋傞暲傋曽傪F(n)偲偟傑偡丅
F(1):愒丂敀丂惵偺俁捠傝丂F(1)=3
F(2):愒敀丂敀惵丂惵偺屻偼F(1)偲偍傝丂傛偭偰F(2)=5
F(3):愒敀惵丂敀惵偺偁偲偼俥乮侾乯偲偍傝丂惵偺屻偼F(2)偲偍傝
丂丂傛偭偰F(3)=1+3+5=9
F(4):愒敀惵偺屻偼F(1)偲偍傝丂敀惵偺屻偼F(2)偲偍傝丂惵偺屻偼F(3)偲偍傝
丂丂傛偭偰F(4)=F(1)+F(2)+F(3)=3+5+9=17捠傝
堦斒偵n>3偱偼丂F(n)=F(n-1)+F(n-2)+F(n-3)偑惉傝棫偪傑偡偹丅
傗偼傝梊憐捠傝僩儕儃僫僢僠悢楍偵側傝傑偡丅
俀
n屄暲傋偰嵟屻偑愒偵側傞暲傋曽傪G(n)偲偍傝偲偟傑偡丅
G(1):愒丂偟偐側偄丂G(1)=侾
G(2):愒敀偼偩傔丂敀惵偼偩傔丂惵偺屻偼G(1)偲偍傝丂G(2)=侾
G(3):愒敀惵偼偩傔丂敀惵偺偁偲偼G(1)偲偍傝丂惵偺屻偼G(2)偲偍傝
丂丂G(3)=G(1)+G(2)=2
G(4):愒敀惵偺屻偼G(1)偲偍傝丂敀惵偺屻偼G(2)偲偍傝丂惵偺屻偼G(3)偲偍傝
丂丂G(4)=G(1)+G(2)+G(3)=1+1+2=4
G(5):愒敀惵偺屻偼G(2)偲偍傝丂敀惵偺屻偼G(3)偲偍傝丂惵偺屻偼G(4)偲偍傝
丂丂G(4)=G(2)+G(3)+G(4)=1+2+4=7
G(6):愒敀惵偺屻偼G(3)偲偍傝丂敀惵偺屻偼G(4)偲偍傝丂惵偺屻偼G(5)偲偍傝
丂丂G(4)=G(3)+G(4)+G(5)=2+4+7=13
偙傟傕僩儕儃僫僢僠悢楍偱偡偹丅
偝偰栤戣偼乽俋屄暲傋偨偲偒丄嵍偼偟傕塃偼偟傕愒偵側傞乿偺偱偡偑
嵍偐傜愒敀惵偲暲傇偺偱偺偙傝6屄偺暲傋曽偼G(6)偲偍傝丂偮傑傝13捠傝偑夝摎偱偡

| kiyo | 傗側偣 | 僗僠儏乕僨儞僩 |
| 僪儔 | 彑塝幪偰傞憿 | 昹揷丂柧枻 |
| teki | 奰杮丂峗 | 僗儌乕僋儅儞 |
| 崅嫶 摴峀 | 栭傆偐偟偺偮傜偄偍偠偝傫 | 儌儖儌僢僩戝恇 |
| 僒僓儞儅僯傾 | 俙俲 | kirkland |
| 偗傫偨傫 |

傑偢栤戣偺夝庍偺偮偄偰丄幱嵾傪偟側偗傟偽側傝傑偣傫丅
栤戣暥乽愒偺師偼昁偢敀丄敀偺師偼昁偢惵傪暲傋傞傕偺偲偟傑偡乿偲偄偆偲偙傠偱偡偑丄 惓妋偵偼乽愒偺師偵偍偔偲偟偨傜偦傟偼昁偢敀丄敀偺師偵偍偔偲偟偨傜偦傟偼昁偢惵乿偲偄偆昞尰傪偡傋偒偩偭偨 偲巚偄傑偡丅崿棎傪彽偄偰怽偟栿偁傝傑偣傫偱偟偨丅
栤戣偺侾斣偱偡偑丄 teki偝傫丄kirkland偝傫丄崅嫶 摴峀偝傫偐傜偛巜揈偄偨偩偄偨傛偆偵 僩儕儃僫僢僠悢楍偵側傝傑偡丅偮傑傝丄値亜俁偵偮偄偰丄
丂丂丂丂丂F(n)=F(n-1)+F(n-2)+F(n-3)
偑惉傝棫偪傑偡丅側偤側傜丄値屄偺偍偼偠偒偺暲傋曽F(n)偼丄
侾丏愭摢偑惵偺偲偒丄俀斣栚埲崀偼壗偱傕偄偄偺偱丄F(n-1)捠傝丅
俀丏愭摢偑敀偺偲偒丄俀斣栚偼惵丄俁斣栚埲崀偼壗偱傕偄偄偺偱丄F(n-2)捠傝丅
俁丏愭摢偑愒偺偲偒丄俀斣栚偼敀丄俁斣栚偼惵丄係斣栚埲崀偼壗偱傕偄偄偺偱丄F(n-3)捠傝丅
廬偭偰丄F(n)=F(n-1)+F(n-2)+F(n-3)
栤戣偺俀斣偵偮偄偰偼丄懡偔偺曽偑巜揈偝傟偰偄傞傛偆偵丄係斣栚乣俈斣栚偺係偮傪寛傔傟偽偄偄偺偱偡偑丄 俈斣栚偵愒傪抲偔偙偲偑偱偒傑偣傫丅廬偭偰丄 侾斣偺摎偊侾俈捠傝偺拞偐傜枛旜偑愒偵側傞傕偺係捠傝傪彍偗偽偄偄傢偗偱偡偹丅
崅嫶 摴峀偝傫偵傛傟偽丄 枛旜偑愒偵側傞暲傋曽丄偲偄偆偲傜偊傪偡傞偲偙傟傕傑偨僩儕儃僫僢僠悢楍偵側傞偲偄偆偙偲偱偡偹丅 偦偙傑偱偼巚偄摓傝傑偣傫偱偟偨丅扙朮丅
偍偼偠偒偺怓偼愒丄敀丄惵丄椢偺係怓丅愭偺忦審偵丄惵偺偍偼偠偒偺師偵偍偔偲偟偨傜偦傟偼昁偢椢偲偄偆忦審傪壛偊傞偲 偙傟偼丄壗悢楍偲偄偆偺偱偟傚偆丠

 E-mail
E-mail
 栠傞
栠傞
 top
top