Weekend Mathematics乛栤戣乛栤戣65
俇俆丏崅搙側偮傞偐傔嶼
侾侽墌嬍丄俆侽墌嬍丄侾侽侽墌嬍偑崌傢偣偰俇俈枃偁傝丄 偦偺崌寁嬥妟偼俁係俀侽墌偱偡丅 嶰榊孨偑偦傟偧傟偺枃悢傪悢偊偰崌寁嬥妟傪寁嶼偟偨偲偙傠丄 俀庬椶偺峝壿偺枃悢傪擖傟偐偊偰寁嶼偟偨偺偱俁侾俀侽墌偵側傝傑偟偨丅
侾侽墌嬍丄俆侽墌嬍丄侾侽侽墌嬍偼偦傟偧傟壗枃偢偮偁傝傑偟偨偐丠
僺乕僞乕愭惗偲拞妛擖帋偺嶼悢偵挧愴両
僺乕僞乕丒僼儔儞僋儖
怴挭幮
峛梲妛堾拞妛峑2001擭搙擖帋
乮儁儞僱亅儉丗彑塝幪偰傞憿乯
昐墌俀俁枃丂俆侽墌侾俈枃丂侾侽墌俀俈枃偱偡丅
俁係俀侽亅俁侾俀侽亖俁侽侽墌偱侾侽侽亅俆侽亖俆侽丂丂丂丂侾侽侽亅侾侽亖俋侽丂丂丂丂俆侽亅侾侽亖係侽偩偐傜
昐墌嬍偲屲廍墌嬍傪堦慻擖傟懼偊傞偛偲偵俆侽墌曄傢傞偐傜
俁侽侽亐俆侽亖俇偱丂俇慻擖傟懼偊偨傢偗偱偡丅
偲偙傠偱崱擖傟懼偊偰俁侽侽墌尭偠偨偐傜寢壥丄
昐墌嬍偺曽偑屲廍墌嬍傛傝俇枃懡偄偙偲偑傢偐傞丅
懘偺俇枃俇侽侽墌傪尭偠偨俀俉俀侽墌偱偼昐墌嬍偲屲廍墌嬍偼摨悢偱偡丅
偱丄偦偺6枃傪尭偠偨俇侾枃偑俀俉俀侽墌側傢偗偱偡側丅
偲偙傠偱崱昐墌嬍丄屲廍墌嬍奺乆俀侽枃丄廫墌嬍俀侾枃偲壖掕偡傞偲
俀侽侽侽亄侾侽侽侽亄俀侾侽亖俁俀侾侽偲側偭偰
俁俀侾侽亅俀俉俀侽亖俁俋侽偱丂俁俋侽墌懡偄丅
偲偙傠偱昐墌嬍偲俆侽墌嬍偼摨悢偩偐傜乮侾侽侽亄俆侽乯墌儅僀僫僗丄
乮侾侽亄侾侽乯僾儔僗偲側偭偰丂俁俋侽亐侾俁侽亖俁偱丂寢嬊偺偲偙傠丂
廫墌嬍偼丂乮侾侽亄侾侽乯亊俁亖俇侽墌憹偊偰廫墌嬍偺惓偟偄枃悢偼俀俈枃丅
俇侾亅俀俈亖俁係丂丂丂俁係亐俀亖侾俈丂丂侾俈亄俇亖俀俁偩偐傜
昐墌嬍丂俀俁枃丂丂屲廍墌嬍侾俈枃丂丂廫墌嬍27枃偱偡丅丂

乮儁儞僱亅儉丗儌儖儌僢僩戝恇乯
偝偡偑偵掃婽嶼偱偼偱偒傑偣傫偑偍嫋偟偔偩偝偄丅曽掱幃偱偡丅
10墌嬍丄50墌嬍丄100墌嬍偺枃悢傪偦傟偧傟枃偲偟傑偡(p,q,r 帺慠悢)
戣堄偐傜傑偢p+q+r=67, 10p+50q+100r=3420-----(*)偱偡丅
俀庬椶偺峝壿偺枃悢傪擖傟懼偊偰3120墌丄偲崌寁嬥妟偑尭傝丄慡懱偺枃悢偑晄曄偱偁
傞偙偲偐傜壜擻惈偺偁傞擖傟懼偊偨慻傒崌傢偣偼
1)10墌嬍偲50墌嬍偨偩偟(q亜p)
2)50墌嬍偲100墌嬍偨偩偟(r亜q)
3)10墌嬍偲100墌嬍偨偩偟(r亜p)
偺3庬椶丅偦偙偱偦傟偧傟偺応崌傪峫偊傞丅
1)10墌嬍偲50墌嬍偨偩偟(q亜p)偺応崌
p偲q傪擖傟懼偊傞偺偱10q+50p+100r=3120丄偦傟偲(*) p+q+r=67
10p+50q+100r=3420偐傜40(q-p)=300偲曄宍丅
偙傟偐傜q-p=15/2偱嵟弶偺壖掕偵柕弬偡傞丅傛偭偰1)偼晄揔
2)50墌嬍偲100墌嬍偨偩偟(r亜q)偺応崌
r偲q傪擖傟懼偊傞偺偱10p+50r+100q=3120丄偦傟偲(*) p+q+r=67
10p+50q+100r=3420偐傜偙偺楢棫曽掱幃傪夝偄偰50(r-q)=300, 40r-90q=2450側偳傛傝
r=23, q=17,p=27
3)10墌嬍偲100墌嬍偨偩偟(r亜p)偺応崌
r偲p傪擖傟懼偊傞偺偱10r+50q+100p=3120丄偦傟偲(*) p+q+r=67
10p+50q+100r=3420偐傜 90(r-p)=300偲曄宍丅偙傟偐傜r-p=10/3偱嵟弶偺壖掕偵柕弬
偡傞丅傛偭偰3)傕晄揔
埲忋偐傜媮傔傞枃悢偼 偦傟偧傟10墌嬍(27枃), 50墌嬍(17枃), 100墌嬍(23枃)
偲偟傑偟偨丅

乮儁儞僱亅儉丗judas乯
10墌嬍丄50墌嬍丄100墌嬍偺悢傪偦傟偧傟X, Y, Z偲偡傞丅
50墌嬍傪巊傢偢10墌嬍偲100墌嬍偺傒偱栤戣偺慜抜傪枮偨偡偙偲偑偱偒傞偐傪峫偊傞丅
楢棫曽掱幃丂X+Z=67丂10X+100Z=3420丂傪夝偔丅
X=328/9偲側傝丄惍悢偵側傜側偄偺偱戣堄傪枮偨偝偢丄50墌嬍偼彮側偔偲傕1枃偁傞偙偲偑傢偐傞丅丒丒丒嘆
67枃偑慡晹50墌嬍偩偲偡傞偲3420墌偵偲偳偐側偄偐傜丄100墌嬍傕彮側偔偲傕1枃偁傞偙偲偑傢偐傞丅
10墌嬍偑彮側偔偲傕2枃昁梫側偺偼柧傜偐丅
100墌嬍偺悢傪Z偲偡傞偲10墌嬍偲50墌嬍偺悢偺崌寁偼67-Z偲側傞丅
嘆傛傝50墌嬍偑彮側偔偲傕堦偮偁傞偙偲偐傜丄偙偺67-X枃傪偡傋偰10墌嬍偵偡傞偲3420墌偵偲偳偐側偄丅
媡偵峫偊傞偲丄100墌嬍傪彍偄偨巆妟3420-100Z傪慡晹10墌嬍偵偡傞偲丄崌寁枃悢偑67-Z傪偼傞偐偵挻偊偰偟傑偆丅
偙偺偲偒丄10墌嬍偺悢傪5枃堷偄偰50墌嬍傪1枃捛壛偡傞丄偲偄偆挷惍偱3420墌偲側傟偽慜抜傪枮偨偡丅丒丒丒嘇
偙偺嘇偺曽朄偩偲1夞挷愡偡傞偛偲偵崌寁枃悢偑4枃尭傞偙偲偵側傞丅
偮傑傝丄Z偲巆傝傪慡偰10墌嬍偲偟偨偲偒偺崌寁偲67偲偺嵎偑4偺攞悢偱偁傟偽偙偺挷惍偑壜擻偲側傞丅丒丒丒嘊
幃偵偡傞偲丄Z+(3420-100Z)/10-67=4n丂偑惉傝棫偮Z傪峫偊傞丅
仺丂Z+342-10Z-67=4n
仺丂275-9Z=4n丂傪枮偨偡Z傪峫偊傞丅
Z偑婏悢側偺偼柧傜偐側偺偱丄Z=1偺偲偒275-9=266偲側傝4偺攞悢偲側傜側偄丅
Z=3偺偲偒275-27=248偲側傝4偺攞悢偲側傞丅
偙傟埲崀偼Z偺憹壛偵傛傞9Z偺憹壛暘偑4偺攞悢偲側傟偽偄偄偐傜丄36偢偮丄
偮傑傝Z偼4偢偮憹傗偣偽傛偄丅
Z=7 275-63=212
Z=11 275-99=176
Z=15 275-135=140
Z=19 275-171=104
Z=23 275-207=68
Z=27 275-243=32
埲忋偺7偮偺応崌偵挷惍偑壜擻偲側傝丄奺応崌偵偮偄偰偺偙傝偺X偲Y偵偮偄偰楢棫曽掱幃偱偦傟偧傟偺枃悢傕媮傔傜傟傞丅
(2,62,3)
(7,53,7)
(12,44,11)
(17,35,15)
(22,26,19)
(27,17,23)
(32,8,27)
偺偲偒丄崌寁枃悢偑67枃偐偮崌寁妟偑3420墌偲側傞丅
偙偺3庬椶偺峝壿偺偆偪2偮偺枃悢傪擖傟懼偊偰寁嶼偡傞偲崌寁妟偑3120墌偲側傞丅
偙偺偲偒丄擖傟懼偊曽偼10墌嬍偲50墌嬍丄10墌嬍偲100墌嬍丄50墌嬍偲100墌嬍偺3捠傝偟偐側偄丅
10墌嬍傪偳傟偐偲擖傟懼偊傞偲壖掕偡傞丅
抂悢偺20墌偲偄偆偙偲偐傜丄擖傟懼偊偨屻偺10墌嬍偺枃悢偼5n+2偲側傜側偗傟偽側傜側偄丅
偙傟傪枮偨偡Y偍傛傃Z傪娷傓慻傒崌傢偣偼
(2,62,3)偺Y
(7,53,7)偺Z
(27,17,23)偺Y
(32,8,27)偺Z
偺5捠傝偁傞丅
傑偨丄擖傟懼偊屻偵崌寁妟偑壓偑偭偨偙偲偐傜丄擖傟懼偊傞傕偆堦曽偺峝壿偺枃悢偼尭傞偙偲偵側傞丅
偡側傢偪丄5n+2傪枮偨偡Y傑偨偼Z偼X傛傝戝偒偔側偗傟偽側傜側偄丅
摨偠応崌偵偼擖傟懼偊偰傕曄壔偑側偄偙偲偼尵偆傑偱傕側偄丅
偙偺2偮偺忦審傪枮偨偡慻傒崌傢偣偼(2,62,3)偲側傞偑丄擖傟懼偊屻偺崌寁妟偑
62*10+2*50+3*100=1020偲側傝丄戣堄傪枮偨偝側偄丅
偟偨偑偭偰丄10墌嬍偼擖傟懼偊側偄偙偲偑傢偐傞丅丒丒丒嘋
50墌嬍偲100墌嬍傪擖傟懼偊傞嵺偵傕丄擖傟懼偊屻偵崌寁妟偑壓偑傞偙偲偐傜丄
100墌嬍偺枃悢偑尭傞丄偡側傢偪Y 亪埲忋偵傛傝丄偦傟偧傟偺枃悢偼27枃丄17枃丄23枃偱偁傞丅
乮儁儞僱亅儉丗俢俢俿乯 乵忬嫷挷傋偲尵偄栿乶 乵幚峴乶 乵夝偔乶 摎偊丏10墌嬍27枃丆50墌嬍17枃丆100墌嬍23枃丏乮偱傕斱嫰側夝摎偱偟偨乯
乮儁儞僱亅儉丗嚁乯 10墌嬍偺枃悢傪値丄50墌嬍偺枃悢傪倣丄100墌嬍偺枃悢傪倠偲偍偔 乮儁儞僱亅儉丗yohe乯 10墌嬍傪x,50墌嬍傪y,100墌嬍傪z偟偰丄曽掱幃傪偮偔傞丅 乮儁儞僱亅儉丗僪儔乯 侾侽墌嬍傪倶枃丆俆侽墌嬍傪倷枃丆侾侽侽墌嬍傪倸枃偲偡傞偲丄
倶丆倷丆倸偼偡傋偰惍悢偵側傞丅 乮鶣乯侾侽墌嬍偲俆侽墌嬍偺枃悢傪擖傟偐偊偰寁嶼偟偨偲偡傞偲 乮鶤乯俆侽墌嬍偲侾侽侽墌嬍偺枃悢傪擖傟偐偊偰寁嶼偟偨偲偡傞偲 乮鶥乯侾侽墌嬍偲侾侽侽墌嬍偺枃悢傪擖傟偐偊偰寁嶼偟偨偲偡傞偲 乮鶣乯乮鶤乯乮鶥乯傛傝丄 乮儁儞僱亅儉丗偙偞偭傁乯 侾侽墌亖俀俈枃丄俆侽墌亖侾俈枃丄侾侽侽墌亖俀俁枃 枃悢丂丂亖俀俈亄侾俈亄俀俁亖俇俈
崌寁嬥妟亖侾侽仏俀俈亄俆侽仏侾俈亄侾侽侽仏俀俁亖俁係俀侽墌 夝朄偼丅丅丅丅 偦傟偧傟偺働乕僗偱昞傪嶌傝丄崌寁枃悢俇俈枃丄崌寁嬥妟俁係俀侽墌偲側傞
傛偆偵俆侽墌丄侾侽侽墌偺枃悢傪挷惍偟傑偟偨丅偦傟偲摨帪偵丄侾侽墌偲俆侽墌丄
侾侽墌偲侾侽侽墌丄俆侽墌偲侾侽侽墌偺枃悢傪擖傟懼偊偨帪偺崌寁嬥妟傕寁嶼偟
傑偟偨丅偦偺寢壥丄俆侽墌偲侾侽侽墌偺枃悢傪擖傟懼偊偨偲偒偵俁侾俀侽墌偲側
傞偙偲偑傢偐傝傑偟偨丅 乮儁儞僱亅儉丗昹揷丂柧枻乯 摎偼丆侾侽墌嬍俀俈屄丆俆侽墌嬍侾俈屄丆侾侽侽墌嬍俀俁屄偱偡丏 乮儁儞僱亅儉丗mhayashi乯 俀庬椶偺峝壿偺枃悢傪擖傟懼偊傞慜偺崌寁嬥妟偼俁係俀侽墌丄
擖傟懼偊偨屻偺崌寁嬥妟偼俁侾俀侽墌側偺偱丄
崌寁嬥妟偺嵎偼俁侽侽墌丅 乽俀庬椶偺峝壿乿偺慖戰巿偼
俀庬椶偺峝壿偺枃悢傪擖傟懼偊傞偲崌寁嬥妟偺嵎偑俁侽侽墌偵側偭偨偺偱
俀庬椶偺峝壿偺嵎偺攞悢偑俁侽侽偱側偗傟偽側傜側偄丅
偙傟傪枮偨偡偺偼忋偺(2)偺応崌偺傒丅
偮傑傝乽俀庬椶偺峝壿乿偲偼俆侽墌嬍偲侾侽侽墌嬍偩偭偨偙偲偑傢偐傞丅 屻偼侾侽墌嬍丆俆侽墌嬍丆侾侽侽墌嬍偺枃悢傪
偦傟偧傟 x,y,z 偲偍偄偰俁尦楢棫曽掱幃 乮儁儞僱亅儉丗僗儌乕僋儅儞乯 a+b+c=67 b+5a+10c=312丂側傜丄4乮b-a乯=30丂偩偐傜偩傔丅 彫妛惗偼偳偆傗偭偰夝偔偺偐側乕丅 乮儁儞僱亅儉丗yokodon乯 杔偼偦傫側偵摢偑椙偔側偔偰丄埫嶼偱掃婽嶼偺弌棃傞傛偆側戙暔偱偼側偄偺偱丄僆
乕僜僪僢僋僗偵揇廘偔楢棫曽掱幃偱夝偄偰偟傑偄傑偡丅10墌嬍丄50墌嬍丄100墌嬍偺
枃悢傪偦傟偧傟 x 丄y 丄z 偲偟傑偡丅 x + y + z 亖 65 丂丒丒丒[1] 偝偰丄擖傟懼偊偰悢偊偨応崌偱偡偑丄埲壓偺俁捠傝偑偁傝傑偡丅 埲壓丄奺乆偺応崌傪峫偊傑偡丅 偱丄寢榑偼丄 乮儁儞僱亅儉丗kiyo乯 俁係俀侽-俁侾俀侽亖俁侽侽 摎偊丂侾侽墌嬍丄俀俈枃丂俆侽墌嬍丄侾俈枃丂侾侽侽墌嬍丄俀俁枃 乮儁儞僱亅儉丗崅嫶 摴峀乯 3420-3120=300偱偡偐傜擖傟懼偊傞偲300墌偺嵎偑偱偒傑偡丅 傛偭偰10墌嬍丂27枃丂50墌嬍丂17枃丂100墌嬍丂23枃偲側傝傑偡丅
乮儁儞僱亅儉丗teki乯 摎偊丂侾侽墌俀俈枃丄俆侽墌侾俈枃丄侾侽侽墌俀俁枃 乮儁儞僱亅儉丗傗側偣乯 崱寧偺栤戣偱偡偑丄偁偝偼偐側巹偲偟傑偟偰偼
憤摉偨傝偱崌寁枃悢俇俈枃丄憤嬥妟俁係俀侽墌偵側傞
慻傒崌傢偣傪拪弌偟傑偟偨丅
僸儞僩俀偐傜擖傟懼偊偰崌寁偡傞偲俁侽侽墌彮側偔側傞偺偱
侾侽墌偲俆侽墌偺応崌偼堦枃偁偨傝偺嵎妟偑係侽墌側偺偱偙傟偼僟儊 惓偟偄崌寁嬥妟侾侽侽仏俀俁亄俆侽仏侾俈亄侾侽仏俀俈亖
俀俁侽侽亄俉俆侽亄俀俈侽亖俁係俀侽丒丒價儞僑両 擖傟懼偊偨応崌偺崌寁嬥妟俆侽仏俀俁亄侾侽侽仏侾俈亄侾侽仏俀俈亖
侾侾俆侽亄侾俈侽侽亄俀俈侽亖俁侾俀侽丒丒偙傟傑偨價儞僑両 傫偱傕偭偰偍摎偊偱偡
侾侽墌嬍俀俈枃丅俆侽墌嬍侾俈枃丅侾侽侽墌嬍俀俁枃偱偡丅
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯 偦偺侾 偦偺俀 乮儁儞僱亅儉丗aa乯 10墌嬍丄50墌嬍丄100墌嬍傪偦傟偧傟x枃丄y枃丄z枃偲偡傞偲丄 偙偺嵎(40n丄90n丄50n偺偄偢傟偐)偑丄300墌側偺偱丄
乽擖傟懼偊偨偺偼丄50墌偲100墌丅6枃偺嵎偑偁傞丅乿偙偲丄傑偨丄
擖傟懼偊偨偙偲偵傛偭偰300墌尭偭偨偺偱丄100墌偺枃悢偺曽偑50墌傛傝傕懡偄
偙偲偑傢偐傞丅傛偭偰丄 妋擣偟偰傒傞偲丄50墌偲100墌偺枃悢傪擖傟懼偊偰丄 乮儁儞僱亅儉丗kirkland乯 枃悢傪擖傟偐偊偰俁侽侽墌尭偭偨偺偱丄擖傟偐偊偨偺偼俆侽墌嬍偲侾侽侽墌嬍偱丄
侾侽侽墌嬍偑俆侽墌嬍傛傝傕俇枃懡偄丅
乮侾侽墌嬍偲俆侽墌嬍偩偲嵎偑係侽偺攞悢偵側傝丄侾侽墌嬍偲侾侽侽墌嬍偩偲嵎偑俋
侽偺攞悢偵側傞偺偱晄揔乯 師偺憖嶌偑戝抇晄揋両 偡傞偲丄侾侽墌嬍丄俈俆墌嬍偁傢偣偰俇侾枃偱俀俉俀侽墌丅
屻偼晛捠偺掃婽嶼側偺偱丄徻嵶偼徣棯丅 侾侽墌嬍丒丒丒俀俈枃丄俆侽墌嬍丒丒丒侾俈枃丄侾侽侽墌嬍丒丒丒俀俁枃
乮儁儞僱亅儉丗俛倧倱倱俥乯 3420-3120=300 摎丏100墌23枃丂50墌17枃丂10墌27枃
乮儁儞僱亅儉丗wasmath乯 傑偢丆擖傟偐偊偨俀庬椶傪摿掕偟傑偡丅 侾侽墌嬍偲俆侽墌嬍傪擖傟偐偊傞偲嵎妟偼係侽墌丅 丂丂丂擖傟偐偊偨偺偼俆侽墌嬍偲侾侽侽墌嬍
丂丂丂枃悢偺嵎偼俁侽侽亐俆侽亖俇枃 乭俁係俀侽墌乭偐傜侾侽侽墌嬍俇枃丆傕偟偔偼乭俁侾俀侽墌乭偐傜俆侽墌嬍俇枃
傪庢傝彍偄偨乭俀俉俀侽墌乭偼崌寁偑俇侾枃丆俆侽墌嬍偲侾侽侽墌嬍偼摨悢
偵側偭偰偄傑偡丅偡傋偰侾侽墌嬍偩偲偡傞偲俇侾侽墌偵側傞傢偗偱偡偑丆
侾侽墌嬍俀枃傪俆侽墌嬍侾枃偲侾侽侽墌嬍侾枃偵抲偒姺偊偰峴偔偲丆
侾慻抲偒姺偊傞偛偲偵侾俆侽亅俀侽亖侾俁侽墌偢偮憹偊傞偺偱丆 丂丂丂乮俀俉俀侽亅俇侾侽乯亐侾俁侽亖侾俈慻 抲偒姺偊傟偽傛偄偙偲偵側傝傑偡丅偟偨偑偭偰丆乭俁係俀侽墌乭偺撪栿偼 丂丂丂侾侽墌嬍偼 俇侾亅侾俈亊俀亖俀俈枃丆 側偍丆乭俀俉俀侽墌乭偺撪栿傪峫偊傞戙傢傝偵丆 乭俁係俀侽墌乭偲乭俁侾俀侽墌乭
傪偁傢偣偰丆乽崌寁偑侾俁係枃丆俆侽墌嬍偲侾侽侽墌嬍偼摨悢偱丆
乭俇俆係侽墌乭偺撪栿偼侾侽墌嬍偼媮傔傞枃悢偺俀攞丆俆侽墌嬍偼
媮傔傞枃悢偺俀攞亄俇枃丆 侾侽侽墌嬍偼媮傔傞枃悢偺俀攞亅俇枃乿
偲峫偊傞偙偲傕偱偒傑偡丅 偄偢傟偵偣傛丆乽擖傟偐傢傝偺俀庬椶傪乮惍悢榑揑峫嶡偵傛傝乯摿掕
偡傞乿偙偲偲偦偺俀曄悢傪乽摨悢偵偟偰侾曄悢壔偡傞乿偙偲偑億僀儞僩
偲偄偭偨偲偙傠偱偟傚偆偐丅 屻敿晹暘偼丆暥帤幃偱寁嶼偡傞偲丆
偁傑傝栚棫偨側偄偐傕抦傟傑偣傫丅偙偺栤戣偱婥偯偄偨偺偱偡偑丆
偮傞偐傔嶼偭偰峴楍偺婎杮曄宍偺尨宆偩偭偨傫偱偡偹丅
乮儁儞僱亅儉丗俶偲乣乯 俀庬椶偺峝壿傪娫堘偊偰丄嬥妟偺嵎偑俁侽侽墌丅侾侽墌偲俆侽墌偱傕丄侾侽墌偲侾侽侽
墌偱傕側偔丄娫堘偊偨偺偼俆侽墌偲侾侽侽墌偩偲偄偆偙偲偑傢偐傞丅偙傟偝偊傢偐傟偽俁
尦堦師楢棫曽掱幃偱夝偗傞偺偩偗傟偳丄丒丒丒丅 偙偨偊丒丒丒侾侽侽墌嬍偑俀俁枃丅俆侽墌嬍偑侾俈枃丅侾侽墌嬍偑俀俈枃丅 偙傟傪俶偲乣偑柤晅偗傞偲丄掃婽嶼偱偼側偔丄亀幹鍜鍘嶼亁偲側傝傑偡丅
偙傟傪摉偰偼傔偰傒傞偲丄
27*10+23*50+17*100=3120
32*10+27*50+8*100=2470

夝摎丒偦偺係
偮傞偐傔嶼側偺偱丄暥帤幃傪巊偊偽娙扨偵側傞偼偢丅
偱傕丄偮傞偐傔嶼偱偦傟偼偛朄搙丒丒丒丅
偱傕偱傕暥帤幃傪巊偭偰傕杮幙偼偮傞偐傔嶼偲摨偠敪憐偺偼偢丒丒丒偲偄偆偐丄
偮傞偐傔嶼傪栚偵尒偊傞宍偵偟偨偺偑暥帤幃丅偲偄偆傢偗偱偛梕幫傪丒丒丒丅
10墌嬍傪x枃丆50墌嬍傪y枃丆100墌嬍傪z枃偲偡傞丅x丆y丆z偼0埲忋偺惍悢丅嫟捠忦審偼丄
丂丂10x亄50y亄100z亖3420 (1)
丂丂丂x亄 y亄 z亖 67 (2)
丂丂50x亄10y亄100z亖3120 (3-1)
偑昁梫丅(1)亅(3-1)偼丄
丂丂亅40x亄40y亖300
丂丂40(亅x亄y)亖300 (4-1)
偲側傝丄(亅x亄y)偼惍悢側偺偱300偼40偺攞悢偱偁傞偙偲偑昁梫丅偙傟偼晄壜丅
丂丂100x亄50y亄10z亖3120 (3-2)
偑昁梫丅(1)亅(3-2)偼丄
丂丂亅90x亄90z亖300
丂丂90(亅x亄z)亖300 (4-2)
偲側傝丄(亅x亄z)偼惍悢側偺偱300偼90偺攞悢偱偁傞偙偲偑昁梫丅偙傟傕晄壜丅
丂丂10x亄100y亄50z亖3120 (3-3)
偑昁梫丅(1)亅(3-3)偼丄
丂丂亅50y亄50z亖300
丂丂50(亅y亄z)亖300 (4-3)
偲側傝丄(亅y亄z)偼惍悢側偺偱300偼50偺攞悢偱偁傞偙偲偑昁梫丅偙傟偼OK偱丄
丂丂丂亅y亄z亖6 (3)
偲側傞丅
丂丂10x亄50y亄100z亖3420 (1)
丂丂丂x亄 y亄 z亖 67 (2)
丂丂丂丂丂亅y亄 z亖 6 (3)
(3)傛傝丄z亖y亄6 (3')
(3')傪(1)偲(2)偵戙擖偟丄
丂丂10x亄150y亖2820 (1')
丂丂丂x亄 2y亖 61 (2')
傪摼傞丅 (2')傛傝丄
丂丂x亖亅2y亄61 (2'')
(2'')傪(1')偵戙擖偟丄
丂丂丂10x亄150y亖10(亅2y亄61)亄150y
丂丂丂丂丂丂丂亖亅20y亄610亄150y
丂丂丂丂丂丂丂亖130y亄610 亖2820
偱丄
丂丂130y亄610亖2820
丂丂丂丂丂13y亖 221
丂丂丂丂丂丂y亖 17 (4)
(4)傪(2'')偲(3')偵戙擖偟丄
丂丂x亖亅2y亄61亖亅34亄61亖27
丂丂z亖 y亄 6亖 17亄 6亖23
偲側傞丅

夝摎丒偦偺俆
丂丂値亄倣亄倠亖67 10値亄50倣亄100倠亖俁係俀侽
偡傞偲擖傟懼偊偰偟傑偭偨偺偼
丂丂10倣亄50値亄100倠亖3120丒丒丒嘆
丂丂10倠亄50倣亄100値亖3120丒丒丒嘇
丂丂10値亄50倠亄100倣亖3120丒丒丒嘊
偺俁捠傝偱偁傞丅
嘆丆嘇偱偼夝偑帺慠悢偱側偄偨傔丅
嘊偱夝偔偲
丂丂値亖27 倣亖17 倠亖23
摎偊10墌嬍27枃50墌嬍17枃100墌嬍23枃

夝摎丒偦偺俇
丂丂丂丂x+5y+10z=342乧(1)
丂丂丂丂x+y+z=67乧乧乧(2)
師偵2偮偺幃偺x,y,z傪偦傟偧傟楢棫偟偰夝偔丅
丂丂丂丂4y+9z=275乧乧(3)
丂丂丂丂5z-4x=7乧乧乧(4)
丂丂丂丂9x+5y=328乧乧(5)
崱搙偼,嘆偺幃偐傜x,y,z偺偆偪2偮傪擖傟懼偊傞偲丄
丂丂丂丂z+5y+10x=312乧(6)
丂丂丂丂y+5x+10z=312乧(7)
丂丂丂丂x+5z+10y=312乧(8)
偺3偮偺幃偑側傞丅偙偺偆偪1偮偺幃偑惓偟偄偐傜丄偦傟偧傟偺幃傪(2)偺幃偲楢棫偝
偣偰夝偔丅
(6)偼9x+4y=245丅偙傟偵(5)偺幃傪楢棫偟偰夝偔偲丄y=83偲側偭偰偟傑偄y偺尷搙傪挻
偊傞偺偱堘偆丅
(7)偼4x+9z=245丅偙傟偵(4)偺幃傪楢棫偟偰夝偔偲丄x=83/4偲側傝丄帺慠悢偱側偄偺
偱堘偆丅
(8)偼9y+4z=245丅偙傟偵(3)偺幃傪楢棫偟偰夝偔偲丄y=17丄z=23偲側傞偺偱丄
(2)偺幃偐傜x=27偑暘偐傞丅
偙傟傪(1)丄(8)偵戙擖偟偰傕丄偁偭偰偄傞偺偱丄
傛偭偰丄10墌嬍27枃丄50墌嬍17枃丄100墌嬍23枃

夝摎丒偦偺俈
倶亄倷亄倸亖俇俈
侾侽倶亄俆侽倷亄侾侽侽倸亖俁係俀侽
俆侽倶亄侾侽倷亄侾侽侽倸亖俁侾俀侽
偙偺帪丄夝偼偡傋偰惍悢偵側傜側偄偺偱丄晄揔丅
倶亄倷亄倸亖俇俈
侾侽倶亄俆侽倷亄侾侽侽倸亖俁係俀侽
侾侽倶亄侾侽侽倷亄俆侽倸亖俁侾俀侽
夝偼丂倶亖俀俈丆倷亖侾俈丆倸亖俀俁
倶亄倷亄倸亖俇俈
侾侽倶亄俆侽倷亄侾侽侽倸亖俁係俀侽
侾侽侽倶亄俆侽倷亄侾侽倸亖俁侾俀侽
偙偺帪丄夝偼偡傋偰惍悢偵側傜側偄偺偱丄晄揔丅
侾侽墌嬍俀俈枃丆俆侽墌嬍侾俈枃丄侾侽侽墌嬍俀俁枃丅

夝摎丒偦偺俉
俆侽墌偲侾侽侽墌偺枃悢傪擖傟懼偊偰
崌寁嬥妟亖侾侽仏俀俈亄俆侽仏俀俁亄侾侽侽仏侾俈亖俁侾俀侽墌
偲巚偄傑偡丅
崌寁嬥妟偺侾侽侽墌枹枮偺晹暘偑俀侽墌偵側傝傑偡偺偱丄侾侽墌偺枃悢偼
俀枃丄俈枃丄侾俀枃丄侾俈枃丒丒丒丒丒丒俇俀枃丄俇俈枃
偺偄偢傟偐偺偼偢偱偡丅
昞偼俤倃俠俤俴俀侽侽侽偱嶌惉偟傑偟偨偺偱揧晅偟傑偡丅
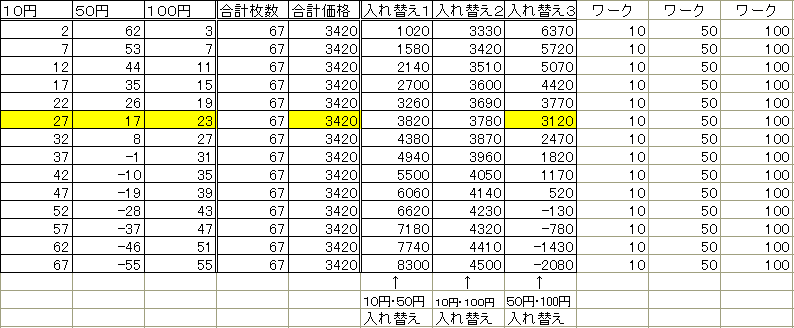

夝摎丒偦偺俋
俆侽墌嬍偲侾侽侽墌嬍偺屄悢傪曄偊傞偲俁侾俀侽墌偵側傝傑偡丏
僄僋僙儖偺儅僋儘偱夝偒傑偟偨丏柺敀偔側偄夝摎偱偡傒傑偣傫丏
Option Explicit
Sub Macro1()
Dim 昐 As Integer
Dim 屲廫 As Integer
Dim 廫 As Integer
Dim a As Integer
Cells(1, 1).Value = 0
Range("A1").Select
For 昐 = 1 To Application.Min(67 - 1 - 1, (3420 - 50 - 10) / 100)
For 屲廫 = 1 To Application.Min(67 - 昐 - 1, (3420 - 100 - 10) / 50)
廫 = 67 - 昐 - 屲廫
If 100 * 昐 + 50 * 屲廫 + 10 * 廫 = 3420 Then
If 100 * 屲廫 + 50 * 昐 + 10 * 廫 = 3120 Then
a = 1
ElseIf 100 * 廫 + 50 * 屲廫 + 10 * 昐 = 3120 Then
a = 2
ElseIf 100 * 昐 + 50 * 廫 + 10 * 屲廫 = 3120 Then
a = 3
Else
a = 0
End If
If a > 0 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 4).Value = 昐
Cells(Cells(1, 1).Value, 3).Value = 屲廫
Cells(Cells(1, 1).Value, 2).Value = 廫
Select Case a
Case 1
Cells(Cells(1, 1).Value, 5).Value = "100<-->50"
Case 2
Cells(Cells(1, 1).Value, 5).Value = "100<-->10"
Case Else
Cells(Cells(1, 1).Value, 5).Value = "50<-->10"
End Select
End If
End If
Next 屲廫
Next 昐
End Sub

夝摎丒偦偺10
丂丂(1)侾侽墌嬍偲俆侽墌嬍
丂丂(2)俆侽墌嬍偲侾侽侽墌嬍
丂丂(3)侾侽墌嬍偲侾侽侽墌嬍
偺俁捠傝偁傞偑偙偙偱俀庬椶偺峝壿偺嵎偵拲栚偟偰傒傞偲
丂丂(1)偺応崌丄俆侽亅侾侽亖係侽墌
丂丂(2)偺応崌丄侾侽侽亅俆侽亖俆侽墌
丂丂(3)偺応崌丄侾侽侽亅侾侽亖俋侽墌
偲側傞丅
丂丂10x+50y+100z=3420
丂丂10x+100y+50z=3120
丂丂x+y+z=67
傪夝偄偰 x=27, y=17, z=23 傪摼傞丅
傛偭偰侾侽墌嬍丆俆侽墌嬍丆侾侽侽墌嬍偼
偦傟偧傟俀俈枃丆侾俈枃丆俀俁枃偁偭偨丅

夝摎丒偦偺11
a+5b+10c=342丂偺帪丄
c+5b+10a=312丂側傜丄9乮c-a乯=30丂偩偐傜偩傔丅
a+5c+10b=312丂側傜丄5乮c-b乯=30丂偐傜丄c-b=6 傛傝丄
b=c-6,a=73-2c丂偲側傝丄
73-2c+5(c-6)+10c=342丂偐傜丄c=23,b=17,a=27丂偲傢偐傞丅

夝摎丒偦偺12
梌忦審偐傜丄傑偢埲壓偺俀幃偑惉傝棫偪傑偡丅
10x + 50y + 100z 亖 3420 丂丒丒丒[2]
乮i乯10墌嬍偲50墌嬍傪擖傟懼偊偨応崌丄
丂丂50x + 10y + 100z 亖 3120 丂丒丒丒[3]
乮ii乯10墌嬍偲100墌嬍傪擖傟懼偊偨応崌丄
丂丂丂100x + 50y + 10z 亖 3120 丂丒丒丒[4]
乮iii乯50墌嬍偲100墌嬍傪擖傟懼偊偨応崌丄
丂丂10x + 100y + 50z 亖 3120 丂丒丒丒[5]
乮i乯偺応崌偵娭偟偰丗乷[2] - [3]乸亐10 偐傜丄師幃傪摼傑偡丅
丂丂4丒(y - x) 亖 30
x 丄y 偼惍悢側偺偱 y - x 傕惍悢偱偁傝丄偙偺応崌偼晄揔偱偡丅
乮ii乯偺応崌偵娭偟偰丗乷[2] - [4]乸亐10 偐傜丄師幃傪摼傑偡丅
丂丂9丒(z - x) 亖 30
x 丄z 偼惍悢側偺偱 z - x 傕惍悢偱偁傝丄偙偺応崌傕晄揔偱偡丅
乮iii乯偺応崌偵娭偟偰丗乷[2] - [5]乸亐10 偐傜丄師幃傪摼傑偡丅
丂丂5丒(z - y) 亖 30
傛偭偰 z - y 亖 6 乮[6] 幃偲偟傑偡乯偲側傝丄偙偺応崌偼揔偟傑偡丅
[1] 妿偮 [2] 妿偮 [5] 偼丄 [1] 妿偮 [2] 妿偮 [6] 偲摨抣側偺偱丄偙偺俁幃偐傜寢嬊
丂丂x 亖 27 丄y 亖 17 丄z 亖 23
傪摼傑偡丅
丂丂10墌嬍丗27枃丄50墌嬍丗17枃丄100墌嬍丗23枃丂乧(摎)
偱偡丅
#杮暔偺掃婽嶼偱偼丄偳傫側姶偠側偺偱偟傚偆丠(^^;

夝摎丒偦偺13
俁侽侽墌彮側偔側偭偰偄傞丅
俁侽侽傪妱傝愗傞偺偼(俁乯偺応崌偱偁傞丅
侾侽墌嬍傪倃枃丄俆侽墌嬍傪倄枃偲偡傞偲丄侾侽侽墌嬍偼乮倄+俇乯枃偲側傞丅
倃+倄+乮倄+俇乯亖俇俈丂丂丂丂丂丂丂丂丂丂丂丂丂丂亅亜丂倃+俀倄亖俇侾
侾侽倃+俆侽倄+侾侽侽*乮倄+俇乯亖俁係俀侽丂丂丂 丂-亜丂X+侾俆倄亖俀俉俀
丂丂丂丂侾俁倄亖俀俀侾
丂丂丂丂丂丂倄亖侾俈
丂丂丂丂丂丂倃亖俀俈
丂丂

夝摎丒偦偺14
偨偲偊偽a墌嬍偲B墌嬍偺枃悢傪庢傝懼偊傞偲偟傑偡丅
a墌嬍偑X枃丄b墌嬍偑Y枃偁傞偲偡傞偲庢傝懼偊偨偲偒偺憹尭偼
(aY+bX)-(aX+bY)=(a-b)(Y-X)偲側傝(a-b)墌偺攞悢偵側傝傑偡丅
10墌嬍偲50墌嬍側傜40偺攞悢偵側傝
50墌嬍偲100墌嬍側傜50偺攞悢偵側傝
10墌嬍偲100墌嬍側傜90偺枃悢偵側傝傑偡丅
300偼50偺攞悢偱偁傝傎偐偺応崌偵摉偰偼傑傜側偄偺偱庢傝懼偊偨偺偼
50墌嬍偲100墌嬍偱偁傞偙偲偑傢偐傝傑偡丅
傑偨300亐50=6傛傝丂偦偺枃悢偺嵎偑6枃偱偁傞偙偲傕傢偐傝傑偡丅
偙偺偲偒丂10墌嬍偺枃悢傪X丄50墌嬍偺枃悢傪Y偲偡傞偲庢傝懼偊偰
偍嬥偑尭偭偨偺偱100墌嬍偺枃悢偼Y+6枃偱丄
10X+50Y+100(Y+6)=3420丂X+Y+Y+6=67偺楢棫曽掱幃傪夝偄偰X=27丂Y=23

夝摎丒偦偺15
亙夝朄亜
乮俆侽墌偲侾侽墌媦傃侾侽侽墌偲侾侽墌偱偼丄嵎偑係侽丄俋侽偲側傞偨傔丄俁侽侽傪妱傝愗傟側偄乯

夝摎丒偦偺16
侾侽偺埵偑俀侽側偺偱侾侽墌嬍偺悢堦寘傔偺悢偼俀偐俈偵側傝
俀偺帪偼俆侽墌嬍偺堦寘傔偺悢帤偼嬼悢偵俈偺帪偼婏悢偵側傝傑偡丅
偨偩偟侾侽墌嬍偺悢偑俁俇枃埲忋偵側傞偲崌寁嬥妟偑俁係俀侽墌傪壓夞傞
偦傫側偙傫側傪僜儘僶儞傪巊偭偰乮塕偱偡乯偳偑偪傖偑傗偭偨偲偙傠
寢嬊偼慡晹偱俈捠傝
侾侽侽墌嬍 俆侽墌嬍 侾侽墌嬍
俀俈 俉 俁俀
俀俁 侾俈 俀俈
侾俋 俀俇 俀俀
侾俆 俁俆 侾俈
侾侾 係係 侾俀
俈 俆俁 俈丂
俁 俇俀 俀
枖侾侽墌偲侾侽侽墌偺応崌傕摨偠條側棟桼偱僟儊
巆傞偲偙傠擖傟懼偊偨偺偼侾侽侽墌偲俆侽墌側偺偱彮側偔側偭偨嬥妟傪
嵎妟偱妱傞偲俇偵側傝傑偡丅偮傑傝侾侽侽墌嬍偺曽偑俆侽墌嬍傛傝俇枃懡偄
慻傒崌傢偣偵側傞丒丒傛偹
愭傎偳偺慻傒崌傢偣偺拞偐傜偙偺忦審偵摉偰偼傑傞偺偼
侾侽侽墌嬍俀俁枃丅俆侽墌嬍侾俈枃丅侾侽墌嬍俀俈枃偙傟偩偗偵側傝傑偡丅
偆乣傫偲丄崌寁嬥妟偁偭偰傑偡傛偹

夝摎丒偦偺17
乮100墌嬍丆50墌嬍丆10墌嬍乯偼丄乮23,17,27乯枃偢偮偱偡丅
100墌嬍丆50墌嬍丆10墌嬍偺枃悢傪偦傟偧傟倶丆倷丆倸偲偍偔偲丄
丂丂丂100倶亄50倷亄10倸亖3420丂丒丒丒乮侾乯
丂丂丂倶亄倷亄倸亖俇俈丂丒丒丒丒丒丒丒丒乮俀乯
乮侾乯偵偍偄偰丄100墌嬍偲50墌嬍偺枃悢傪擖傟偐偊偨傕偺丄50墌嬍偲10墌嬍
偺枃悢傪擖傟偐偊偨傕偺偼偦傟偧傟
丂丂丂100倷亄50倶亄10倸丂丒丒丒丒丒丒乮俁乯
丂 丂 100倶亄50倸亄10倷丂丒丒丒丒丒丒乮係乯
偝偰丄乮侾偺嵍曈乯亅乮俁乯亖50乮倶亅倷乯丄乮侾偺嵍曈乯亅乮係乯亖40乮倷亅倸乯偱偡丅
崌寁嬥妟偲俀庬椶偺峝壿偺枃悢傪擖傟偐偊偰寁嶼偟偨傕偺偲偺嵎
3420亅3120亖300 偼丄50偺攞悢側偺偱丄100墌嬍偲50墌嬍傪擖傟偐偊偰寁嶼偟偨
偙偲偵側傝傑偡丅乮俁偺応崌乯
丂丂丂50乮倶亅倷乯亖300傛傝
丂丂丂倶亅倷亖俇丂丒丒丒丒丒丒丒丒丒丒丒丒乮俆乯
忋偺乮侾乯丆乮俀乯丆乮俆乯傪楢棫偟偰夝偔偲 倶亖23丆倷亖17丆倸亖27 偲側傝傑偡丅
100墌嬍丆50墌嬍丆10墌嬍偺枃悢傪偦傟偧傟倶丆倷丆倸偲偍偒傑偡丅
傑偨丄乮100墌嬍丆50墌嬍丆10墌嬍乯偼偦傟偧傟偺枃悢偺峝壿偺崌寁嬥妟偲偟傑偡丅
傑偢丄100墌嬍偲10墌嬍傪壗枃偐偁傢偣偨傕偺偲50墌嬍壗枃偐偑丄嬥妟偲枃悢
偑摨偠偵側傞傛偆偵峫偊傞偲丄
丂丂丂100倶亄10倸亖50倷丂丒丒丒乮俇乯
丂丂丂倶亄倸亖倷丂丒丒丒丒丒丒乮俈乯
乮俇乯丆乮俈乯傪楢棫偝偣傞偲丄倶亖4丆倷亖9丆倸亖5丏
偮傑傝丄100墌嬍傪4枃偲10墌嬍傪5枃尭傜偟偰傕丄50墌嬍傪9枃憹傗偣偽嬥妟偲枃
悢偵曄壔偼偁傝傑偣傫丅
師偵丄崌寁嬥妟偲俀庬椶偺峝壿偺枃悢傪擖傟偐偊偰寁嶼偟偨傕偺偲偺嵎偼丄
丂丂丂3420亅3120亖300
偙傟偼丄50偺攞悢側偺偱丄峝壿偺枃悢偺擖傟偐偊偼丄100墌嬍偲50墌嬍偵偮偄偰偱偡丅
丂丂丂乮100倶亄50倷亄10倸乯亅乮100倷亄50倶亄10倸乯
丂丂丂亖50乮倶亅倷乯亖300 丂丒丒丒乮俉乯
乮俉乯傛傝 倶亖倷亄俇
偮傑傝丄100墌嬍偺枃悢偼50墌嬍偺枃悢傛傝俇枃懡偄偲偄偆偙偲偱偡丅
忋偺俀偮偺偙偲傪摢偵偍偄偰栤戣傪峫偊偰偄偒傑偡丅峝壿67枃偑慡晹10墌嬍偲
偟偰傒傑偟傚偆丅乮0丆0丆67乯亖670丏偡傞偲丄 3420亅670亖2750 墌晄懌偱偡丅
偙偙偱丄10墌嬍傪100墌嬍偲岎姺偡傞偲1枃偁偨傝 90墌 憹偊傑偡丅
丂丂丂2750亐90亖30偁傑傝50
偱偡偐傜10墌嬍傪30枃100墌嬍偲岎姺偟傑偡丅乮30丆0丆37乯亖3370丏偱傕傑偩50
墌乮偁傑傝偺暘乯晄懌偱偡丅10墌嬍傪50墌嬍偲岎姺偡傞偲40墌憹偊傑偡偑50墌偵
偼側傝傑偣傫丅偦偙偱晄懌偺妟偑40偺攞悢偵側傞傛偆偵100墌嬍傪10墌嬍偵1枃偢
偮栠偟偰偄偒傑偡丅
丂丂丂50亄90亄90亄90亄丒丒丒丒
偡傞偲100墌嬍傪3枃栠偟偨偲偙傠偱320墌晄懌偵側傝40偺攞悢偵側傝傑偡丅
乮27丆0丆40乯亖3100丏
丂丂丂320亐40亖8丏
偦偙偱10墌嬍傪8枃50墌嬍偲岎姺偟偰丄偲傝偁偊偢崌寁偑3420墌偵側傝傑偡丅
乮27丆8丆32乯亖3420丏偙偺応崌偼100墌嬍偲50墌嬍偺枃悢偺嵎偼19枃側偺偱丄摨
嬥妟偱偦偺嵎偑6枃偵側傞傛偆偵偟傑偡丅乮23丆17丆27乯亖3240丏傕偪傠傫
乮17丆23丆27乯亖3120偲側傝傑偡丅

夝摎丒偦偺18
丂丂丂x+y+z=67 .............. (1)
丂丂丂10x+50y+100z=3420 ..... (2)
偝偰丄10墌偲50墌偺枃悢傪擖傟懼偊傞偲丄崌寁妟偱40n(n偼丄10墌偲50墌偺枃悢偺嵎)偺憡堘偑弌傞丅
摨條偵丄10墌偲100墌偱偼丄90n丄50墌偲100墌偱偼丄50n丅
丂丂丂y+6=z .................. (3)
(3)傪(1)(2)偵戙擖偟偰丄
丂丂丂x+2y=61 ................ (4)
丂丂丂10x+150y=2820 .......... (5)
(4)偐傜 x=61-2y 側偺偱丄偙傟傪(5)偵戙擖偟偰丄
丂丂丂610-20y+150y=2820
丂丂丂130y=2210
丂丂丂y=17
傛偭偰丄(4)偐傜 x=61-2*17=27
(3)偐傜 z=17+6=23
10墌27枃(270墌)+50墌17枃(850墌)+100墌23枃(2300墌)偱丄67枃(3420墌)
10墌27枃(270墌)+50墌23枃(1150墌)+100墌17枃(1700墌)偱丄67枃(3120墌)

夝摎丒偦偺19
侾侽侽墌嬍俇枃傪彍偔偲丄巆傝俇侾枃偱俀俉俀侽墌丅
侾侽侽墌嬍偲俆侽墌嬍偑摨悢偁傞偺偱丄侾侽侽墌嬍偺係暘偺侾傪嶍偭偰俆侽墌嬍偵
偔偭偮偗偰偟傑偄乮堘朄峴堊偩両乯丄
慡晹俈俆墌嬍偵偡傞両丠

夝摎丒偦偺20
100-50=50,100-10=90,50-10=40
(偙偺側偐偱300傪妱傝愗傟傞偺偼50偱偡
偩偐傜庢傝堘偊偨偺偼100墌偲50墌)
300亐50=6
(偙傟偑丄100墌偲50墌偺枃悢偺嵎
偱偡偐傜100墌偲50墌傪摨悢偵偦傠偊偨
10墌丄50墌丄100墌崌傢偣偰61枃偺崌寁偼)
3420-100x6=2820
2820=150x18+10x12乧18x2+12=48枃
=150x17+10x27乧17x2+27=61枃
(敪尒両)
17+6=23

夝摎丒偦偺21
侾侽墌嬍偲侾侽侽墌嬍傪擖傟偐偊傞偲嵎妟偼俋侽墌丅
俆侽墌嬍偲侾侽侽墌嬍傪擖傟偐偊傞偲嵎妟偼俆侽墌丅
偙偺偆偪丆俁係俀侽亅俁侾俀侽亖俁侽侽墌偺栺悢偼俆侽墌偩偗側偺偱丆
丂丂丂俆侽墌嬍偼 侾俈枃丆 侾侽侽墌嬍偼 侾俈亄俇亖俀俁枃 乮摎乯

夝摎丒偦偺22
俆侽墌嬍傛傝傕侾侽侽墌嬍偺曽偑俇枃懡偄丅
俇俈枃慡晹偺壙抣傪侾侽墌偢偮尭偠傞偲丄俁係俀侽亅俇俈侽亖俀俈俆侽墌丅係侽墌嬍
乮尦俆侽墌嬍乯偲俋侽墌嬍乮尦侾侽侽墌嬍乯傪偁傢偣偰俀俈俆侽墌偵側傞丅俋侽墌嬍偺曽
偑俇枃懡偄偺偩偐傜丄偦偺俇枃偵徚偊偰傕傜偆偲丄俀俈俆侽墌乕俆係侽墌亖俀俀侾侽墌丅
係侽墌嬍偲俋侽墌嬍偺枃悢偑懙偭偨偺偱丄俀俀侾侽墌亐侾俁侽墌亖侾俈丒丒丒丒係侽墌嬍
偼侾俈枃丅俋侽墌嬍偼侾俈枃亄俇枃亖俀俁枃丅侽墌嬍乮尦侾侽墌嬍乯偼俇俈枃乕乮侾俈枃
亄俀俁枃乯亖俀俈枃丅
専嶼偡傞丅俀俁亊侾侽侽亄侾俈亊俆侽亄侾侽亊俀俈亖俁係俀侽乮偳乕偩偭両乯

惓夝幰
teki kiyo 偙偞偭傁
俶偲乣 儌儖儌僢僩戝恇 俛倧倱倱俥
judas yohe wasmath
彑塝幪偰傞憿 栭傆偐偟偺偮傜偄偍偠偝傫 僗儌乕僋儅儞
傗側偣 嚁 俢俢俿
崅嫶 摴峀 aa 僪儔
昹揷丂柧枻 kirkland yokodon
mhayashi

傑偲傔
巹傕娷傔丄戝恖偺敪憐偼枹抦悢俁偮偺楢棫曽掱幃偱偟傚偆偐丠
崌寁枃悢偑俇俈枃丄崌寁嬥妟偑俁係俀侽墌丄偙偙傑偱偼偡偖偵曽掱幃偵偱偒傑偡丅
俁偮傔偺忦審丄俀庬椶偺峝壿偺枃悢傪擖傟偐偊偰寁嶼偟偨偺偱俁侾俀侽墌丄
偙傟傪幃偵偡傞偵偼応崌暘偗丠
擖傟懼偊偨峝壿偺嵎妟偑丄俁係俀侽亅俁侾俀侽亖俁侽侽偺栺悢偵側偭偰偄側偗傟偽側傜側偄偲偄偆
偙偲偵婥偯偗偽丄擖傟懼偊偨峝壿偼俆侽墌嬍偲侾侽侽墌嬍偩偲偄偆偙偲丄
峏偵侾侽侽墌嬍偺曽偑俇枃懡偄偲偄偆偙偲偑傢偐傝傑偡丅
偙傟偱俁偮傔偺忦審傪幃偵昞偡偙偲偑偱偒傑偡丅傕偟偔偼俀尦楢棫曽掱幃偵偱偒傑偡丅
乮俆侽墌嬍偺枃悢傪倷偲偡傟偽丄侾侽侽墌嬍偺枃悢偼倷亄俇偱偡丅乯
俀尦楢棫曽掱幃傪夝偄偰傕傕偪傠傫偄偄偺偱偡偑丄掃婽嶼偵偙偩傢傞側傜丄
嬶懱揑偵偼偳偆偟偨傜偄偄偐丠丂
俛倧倱倱俥偝傫傗wasmath偝傫丄kirkland偝傫偺傛偆偵丄
侾侽侽墌嬍俇枃傪彍偒丄巆傝俇侾枃偱俀俉俀侽墌偱
峫偊傟偽偄偄傢偗偱偡偹丅
kirkland偝傫偼丄俈俆墌嬍傪嶌偭偰偟傑偆偲偄偆戝抇側傾僀僨傿傾偱偟偨偑丄
巹偼侾俆侽墌嬍傪嶌偭偰偟傑偊偽偄偄偐側丠丂偲巚偄傑偟偨丅
俛倧倱倱俥偝傫傗wasmath偝傫偲摨偠敪憐偱偡丅
峏偵戝抇側傾僀僨傿傾偑俶偲乣偝傫偺亀幹鍜鍘嶼亁乮拲乽傊傃偲偐偘偞傫乿偲撉傒傑偡丅by丂Junko乯
幹偵偼懌偑偁傝傑偣傫傕偺偹丅

 E-mail
E-mail
 栠傞
栠傞
 top
top