Weekend Mathematics/問題/問題61
61.2002年の問題
2002年、新年あけましておめでとうございます。
さて、「2002」という数字は、逆さまからよんでもやはり「2002」となります。
数字の回文?
そこで数字の回文についての問題です。
偶数桁の数字の回文(もちろん自然数)は、必ず11で割り切れるという性質があります。
適当なもので試してみてください!!
そしてこれを証明してください。
注)回文:「しんぶんし」、「たけやぶやけた」など逆さによんでもかわらないもの
(ペンネ−ム:スチューデント)
10・a+bを、abと表すことにします。
ここに、ある偶数桁の数、
abcde...xyzzyx...edcba
があったとします。
ここで、zz000000...00は、11の倍数です。(z・11・1000...00)
次に、y00y0000...000は、1001の倍数です。(y・1001・1000...00)
以下同様に
・
・
・
最後にa000......000aは、1000...0001の倍数です。
また、
| 11 | =11*1 |
| 1001 | =11*91 |
| 100001 | =11*9091 |
| 10000001 | =11*909091 |
| ・ | |
| ・ | |
| ・ |

(ペンネ−ム:こざっぱ)
数字の回文「ABCDE・・・・EDCBA」を、
同じ数字の部分に注目して、加算の式で表すと
| ABCDE・・・・EDCBA | = A0000・・・・0000A |
| + 0B000・・・・000B0 | |
| + 00C00・・・・00C00 | |
| + 000D0・・・・0D000 | |
| ・ | |
| ・ | |
| ・ |

(ペンネ−ム:judas)
まず、11は11で割り切れる。あたりまえですね。
次に、1001=11+990=11+11・90 なのでやはり割り切れる。
同様に、100001、10000001など偶数桁で両端が1で中の数字が全部0
の場合は
すべて 11+999.......990 (9は偶数個)となるので、11で割り切れる。
任意の偶数桁の数字の回文は、
ABCD......DCBA=A00.........00A+B00..........00B・10+C00........00C・100+D00...
........00D・1000+.....0000
と対になっている数字をそれぞれ取り出して分解すると、
それぞれが上記の「偶数桁で両端が1で中の数字が全部0の場合の数」の倍数とな
る。
したがって、偶数桁の数字の回文は常に11で割り切れる。

(ペンネ−ム:とうがらし)
まず、8桁の数字abcddcbaについて考えてみます。
| 11= | 1×11 |
| 1001= | 91×11 |
| 100001= | 9091×11 |
| 10000001= | 909091×11 |
| abcddcba | =a×10000001+10b×100001+100c×1001+1000d×11 |
| =a×909091×11+10b×9091×11+100c×91×11+1000d×11 | |
| =(909091a+90910b+9100c+1000d)×11 |
一般に、
0が2n-2個連なる2n桁(n>3)の数100....01は、
90がn-2連なり最後が91で終わる数9090....91と
11との積で表せる。
すなわち、
1000....01=9090...91×11
また、11=1×11, 1001=91×11だから、
回文数abcd....dcbaは上記n=4(8桁)の例のように
11を因子に持つので11で割り切れる。

(ペンネ−ム:DDT)
偶数桁の数字の回文Aを、
A=a1a2・・・an-1ananan-1・・・a2a1
で表す(2n桁)。ここでn≧1,1≦i≦n,0≦ai≦9で整数、ただしa1≠0。
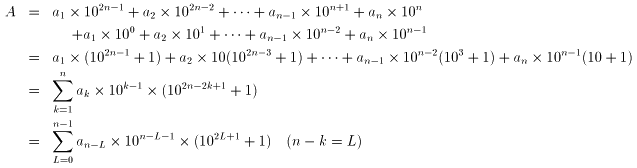
となる。L=0〜n-1を代入した際、102L+1≡10:mode 11 であることを示す。
| 102L+3 | =102L+1・100 |
| ≡10・1:mode 11 | |
| ≡10 :mode 11 |

(ペンネ−ム:teki)
偶数桁の回文となる数字を書き換えると、
a×10・・・01+b×10・・・01×10+・・・・・となります。
これが11の倍数になることを証明すればいいわけです。
従ってこの問題は、要するに102n-1+1が11で割り切れることを証明すればよい
ことになります。
数学的帰納法を用いて証明することとします。
F(n)=102n-1+1とおくと、n=1のとき、F(n)=11 で題意を
満たす。
F(k)=102k-1+1が11の倍数であると仮定すると、
F(k+1)=102k+1+1となる。
ここで、
| F(k+1)−F(k) | =102k+1−102k-1 |
| =102k-1×(100-1) | |
| =99×102k-1 |

(ペンネ−ム:Junbou)
まず102n−1+1が11の倍数であること・・・①を示す。(nは自然数)
(豗) n=1のとき
10+1=11 より成り立つ。
(豩) n=kのとき成り立つと仮定すると
102n−1+1=11A とおける(Aは自然数)
両辺に100をかけると
102n+1+100=1100A
102(n+1)−1+1=11(100A−9) となり
n=k+1のときも成り立つ。
以上(豗)(豩)よりすべての自然数nにおいて102n−1+1は11の倍
数である。
今2m桁(mは自然数)の回文を考えると、条件より以下のように書ける。
102m−1a1+102m−2a2+・・・+10mam
+10m−1am+10m−2am−1+・・・+a1
ここでそれぞれ同じものをまとめると
(102m−1+1)a1+10(102(m−1)−1+1)a2+
102(102(m−2)−1+1)a3+・・・+10m−1
(10+1)am となる。
ここで①より102n−1+1 は11の倍数となるので上式の各項は11の倍
数となる。
つまり2m(偶数)桁の自然数の回文!?は11の倍数となる。

(ペンネ−ム:夜ふかしのつらいおじさん )
この問題の解答の要点は、x+1,x3+1,・・・,x2n-1+1 が、
それぞれ (x+1) を因数に持つことです。
x+1 は明らかです。
x3+1=(x+1)(x2-x+1),
・・・
x2n-1+1=(x+1){x2n-2-x2n-3+x2n-4-・・・+x2-x+1}
のように右辺の右の因数は奇数個の項があり符号が+−+−・・・+と交互になります。
面倒なので、x2n-2-x2n-3+x2n-4-・・・+x2-x+1=x¥(2n-2) と表すことにします。
さて、偶数桁(2n)の数字の回文を a1 a2 a3 ・・・ an an ・・・ a3 a2 a1 とおきます。
ak は各位の数字を表します。
| a1 a2 a3 ・・・ an an ・・・ a3 a2 a1 | |
| = | a1・102n-1+a2・102n-2+a3・102n-3+・・・+an・10n+an・10n-1+・・・+a3・102+a2・10+a1 |
| = | a1・{102n-1+1}+a2・10{102n-3+1}+a3・102{102n-5+1}+・・・+an・10n-1(10+1) |
| = | a1(10+1){10¥(2n-2)}+a2(10+1){10¥(2n-4)}+a3(10+1){10¥(2n-6)}+・・・+an(10+1)(10¥0) |
| = | (10+1)[a1{10¥(2n-2)}+a2{10¥(2n-4)}+a3{10¥(2n-6)}+・・・+an(10¥0)] |
| = | 11[a1{10¥(2n-2)}+a2{10¥(2n-4)}+a3{10¥(2n-6)}+・・・+an(10¥0)] |
偶数桁の 11=11・1,1001=11・91,100001=11・9091,10000001=11・909091,・・・
が分かれば当たり前のことです。

(ペンネ−ム:d3)
数列{a[n]}(n∈N:自然数)を次で定義します:
a[n]:=102n−1+1.
問題の数mは,
項がすべて非負の整数の数列{c[n]}
(ただし,十分に大きなnについては0とする)と,
上の数列{a[n]}を用いて,
m=Σ(j=1・・・),{c[j]×a[j]}
と表せます.
たとえば,m=52344325のとき,
m=4000×a[1]+300×a[2]+20×a[3]+5×a[4]です.
ここでこの問題は,
{a[n]}の項がすべて11で割り切れることを示せば十分です.
a[1]=11はtrivialです.以下はn>1で扱います.
(この1行は本質的ではないけど加えておきます.)
[証明1]
S=1−x+x2+・・・+(−x)2n−2とします.
これは等比数列の和なので,x≠1として,
S={1−(−x)2n−1}/(1+x)
S={1+x2n−1}/(1+x)
すなわち,
1+x2n−1=S×(1+x)
ここで,x=10とすれば,
a[n]={1−10+102+・・・+(−10)2n−2}×11
右辺の前のカッコは正の整数です.よって,11で割り切れます.
[証明2]
a[n]は2n桁の数で,
a[n]=100・・・01.(0は2n−2個続く)
ここで,
a[n]-11=99・・・90.(9は2n−2個続く)
a[n]-11=10×99・・・9.(9は2n−2個続く)
99・・・9.(9は2n−2個続く)はふた桁ごと区切ると,
明らかに11の倍数です.
よって,11で割り切れます.
これでOKだと思います.
最初は数学的帰納法でって考えました.
何となくかきづらくて,まどろっこしいなぁ,と思いつつ.
そんなこんなで,111・・・1を使おうか,とも思いました.
10+1=11だなって思って1番ができました.
ふた桁ごと区切ることを考えて,2番です.
いかがでしょうか?

(ペンネ−ム:浜田 明巳)
この回文数の桁数をn(nは偶数)とすると,この回文数を
| a1×10n−1+a2×10n−2+a3×10n−3+………+an/2×10n/2 | |
| +an/2×10n/2−1+an/2−1×10n/2−2+an/2−2×10n/2−3+………+a1 | |
| = | a1×(10n−1+1)+a2×(10n−2+10)+a3×(10n−3+102) |
| +………+an/2×(10n/2+10n/2−1) | |
| = | a1×(10n−1+1)+a2×10×(10n−3+1)+a3×102×(10n−5+1) |
| +………+an/2×10n/2−1×(10+1) |
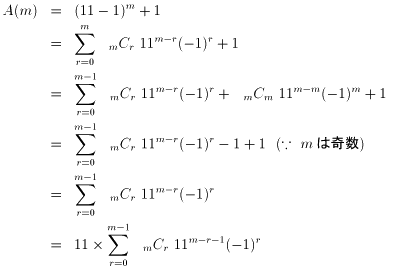
故にA(m)は11の倍数である.
故にこの回文数は,
a1×A(n−1)+a2×10×A(n−3)+a3×102×A(n−5)
+………+an/2×10n/2−1×A(1)
となり,11の倍数であることが分かる.

(ペンネ−ム:yokodon)
まず、以下の補題を示します。
【補題】
bm = 102m+1 +1 (m = 0,1,2,...) は、
全ての非負整数 m に関して11の倍数である。
【証明】
2項定理より、
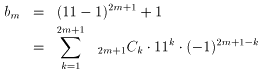
である。この展開結果から明らか。
これを用いて、題意の命題を証明します。
題意のような数字を 2n 桁であるとして、その1位から10n の位までの数字を
a1, a2, ..., an
(但し ak は全て整数で 0 ≦ ak ≦ 9 であり、a1 ≠ 0)と
します。題意のような数 M は以下のように表せます。
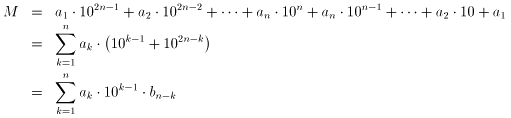
従って、上記の補題より bn-k が11の倍数なので、M も 11 の倍数です。
これにて主張成立です。

(ペンネ−ム:BossF)
偶数桁(2n桁)の回文数N は、
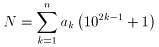
とかけます。ところが
(102k-1+1)=(10+1)(102k-2-102k-3+102k-4-…+1)≡0(mod11)
よって題意は示せました■

(ペンネ−ム:月の光)
F2nを2n桁の自然数とし、
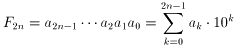
と表わします。
(0≦ak≦9、ただしa0≠0)
条件よりak=a2n-1-kなので
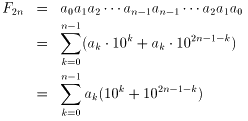
10≡-1 (mod11)なので
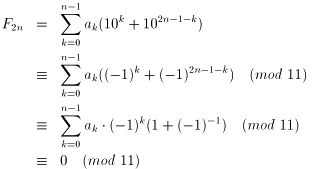
よって『偶数桁の数字の回文(もちろん自然数)は、必ず11で割り切れるという性質』が成り立ちます。

(ペンネ−ム:モルモット大臣)
解答・その1
問題は偶数桁の回文が11で割り切れることを証明することです。
まず全桁数を2N桁(Nは自然数)とします。
1桁目の数をA1,それから順に桁数ごとにA2,A3,.......AN..........A2N-1,A2Nと2N桁までを割り当てます。
そうしますと回文ということから、
A1からANまでのN桁とAN+1からA2NまでのN桁を比較すると
第N桁とN+1桁の間で左右それぞれ対称になっているはずです。
すなわち
AN+1,AN+2,...............A2N-1,A2N=AN,AN-1,................A2,A1という配列です。(#1)
そこで実際の数Bとして表してみると
B=A1×100+A2×101+A3×102+...
AN×10N-1+AN+1×10N+...+A2N-1×102N-2+A2N×102N-1
ここで(#1)より
この式は次のように書き直せます。
B=A1×100+A2×101+A3×102+....+
AN×10N-1+AN×10N+...+A2×102N-2+A1×102N-1
さらにこの式を変形して
B=A1{102N-1+100}+A2{102N-2+101}+.........+AN{10N+10N-1}
とおく。
すなわちBが11で割り切れるためには全ての{}内が11で割り切れればよい。
そこで{}内を一般化しCとおくと
C= 102N-K+10K-1, (Kは1からNまでの自然数)
さてここでCをC=10K-1{102N-2K+1+1}と変形する。
ここで{102N-2K+1+1}に着目してこれをDとおく。
すなわちDが11で割り切れることを示す。
D=102N-2K+1+1である。
しかしこのままでは11で割り切れることを証明するのは難しい。
そこで D=102N-2K+1+1の両辺から11を引き、さらに変形する。
D-11=102N-2K+1+1-11=102N-2K+1-10=10{102(N-K)-1}=10{[102]N-K-1N-K} (#2)
この(#2)式は一般に
Pa-Qa=(P-Q)[Pa-1+QPa-2+......+PQa-2+Qa-1]
の形である。
よって(#2)は
10(102-1){[102]N-K-1+....+1N-K-1}=
90×11{[102]N-K-1+....+1N-K-1}
となり任意のKに対してD-11が11で割り切れることからD-11=11G(Gは自
然数)とおけD=11(G+1)よりDも11で割り切れる。
これからC=10K-111(G+1)よりCも任意のKに対して11で割り切れる。
以上より題意の回文となる数Bは11で割り切れる。
解答・その2
回文の左右の桁数をN桁とする。Nによる数学的帰納法で証明をする。
N=1の時はその数字をPP(Pは1〜9までの自然数)とおく
とPP=10P+P=11Pとなり確かに11の倍数。
ここでN=kの時にこの数をA(k)とし、
11の倍数であると仮定するとA(k)=11m(mは自然数)とおける。
任意の2(k+1)桁の回文をA(k+1)とおく。
先頭と最後の数字は回文より同じで、B(Bも1〜9までの自然数)とおくと
2k桁の回文A(k)を用いて、以下のようにかける。
A(k+1)=B×102k+1+B+A(k)×10
数学的帰納法の仮定により、A(k)は11の倍数なので、A(k)=11mとおける。
よってA(k+1)=B×102k+1+B+A(k)×10=B[102k+1+1]+110m
ここで[102k+1+1]に着目して
C=102k+1+1とおき両辺から11を引いて変形すると
C-11=102k+1+1-11= 102k+1-10=10[102k-1]=10[(102)k-1]となり
10[(102)k-1]=10(102-1){(102)k-1+(102)k-2+.......+102+10+1}
すなわち C-11=990{(102)k-1+(102)k-2+.......+102+10+1}
C=990{(102)k-1+102)k-2+.......+102+10+1}+11で
990=11×90よりCは11の倍数=11t(tも自然数)
最後に A(k+1)=B×11t+110mとなりN=k+1の時も11の倍数。よって数学的帰納法により
題意は証明された。

(ペンネ−ム:高橋 道広)
偶数桁の数字の回文を2n桁としてその数を並べたものを
X=a(1)a(2)...a(k)...a(n)a(n)...a(k)...a(2)a(1)
と書いたとします。
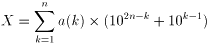
となり、
102n-k+10k-1=10k-1×(102n-2k+1+1)
ですから10(奇数)+1が11で割り切れることを示せばよいことになります。
では問題を「102n-1+1が11で割り切れることを証明せよ」として、これを
解くことにします。
解1 数学的帰納法
n=1のとき 102×1-1+1=11は11で割り切れる。
n=kのとき102k-1+1が11で割り切れると仮定したときに
n=k+1の時、
| 102k+1+1 | =102×102k-1+1 |
| =102×(102k-1+1-1)+1 | |
| =102×(102k-1+1)-100+1 |
解2 二項定理
X=11とする
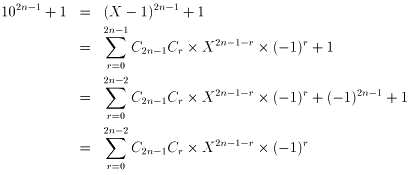
となり、Σの各項はXだ少なくとも1つ含まれているのでXの倍数に
なっている。
よって元の数もX=11の倍数である。
解3 因数分解 または等比数列の和
X=10とする
X2n-1+1=(X+1)(X2n-2-X2n-3+X2n-4-...+1)
と因数分解されるのでX+1=11で割り切れることになる
解4 等比数列の和
これは解3の読み替えみたいな方法ですが...
初項1公比-Xの等比数列の初項から2n-2項までの和は、
1-X+X2-X3+...+(-X)2n-2=(1-(-x)2n-1)/(1+x)
=(1+X)2n-1/(1+X)
X=10とすると、この式の左辺は整数であるから右辺も整数
すなわち(1+X)2n-1は1+X=11で割り切れる。
解5 安直な方法
10...01(2n桁)=999...9990(2n-1桁)+11となる。
このとき右辺の0は偶数個より左辺の9も偶数個つまり
999...9990=9900...00(2n-1桁)+9900...00(2n-3桁)+...+99000(5桁)+990(3桁)
となる。右辺の各数は11で割り切れる(商は900...00の形)
よって明らかに(なんと便利なことばでしょう 明らかに...って)
10...01(2n桁)は11で割り切れる
解6 もっと安直な方法 法(mod)
10=-1(mod 11)より
102n-1+1=(-1)2n-1+1=-1+1=0(mod 11)
よって102n-1+1は11の倍数
以上から元の命題が成り立つことが証明されました。

(ペンネ−ム:T_Tatekawa)
a を自然数として
100・a = (99+1)・a = 9・11・a + a
なので,100・a を 11 で割った余りは a を 11 で割った余りと同じ.
これを繰り返していくと,a・ 100n(n は自然数)を
11 で割った余りは,a を 11 で割った余りと同じになる.
つまり,
pqrs
という数(p, q, r, s は一桁の負でない整数)を 11 で割った
余りは
pq + rs
を 11 で割った余りと同じになる.
さて,今から考えようとしている数は偶数桁の回文なので,
この数が m 桁だとすると
m 桁目の数 = 1 桁目の数
m-1 桁目の数 = 2 桁目の数
m-k 桁目の数 = k+1 桁目の数
m/2+1 桁目の数 = m/2 桁目の数
ということになる.
以後,k 桁目の数を ak と書く事にする.
l を奇数とした場合
回文となっている数を二桁ずつ位取りしていくと
am-l+1 = al
am-l = al+1 (*)
となっている.一方で
am-l+1・10m-l+1 + am-l・10m-l
+ al+1・10l-1 + al・10l-2
を 11 で割った余りは
am-l+1・10 + am-l + al+1・10 + al
を 11 で割った余りとなり,これは (*) の関係から
(al+1 + al)・11
となって 11 で割り切れる.
桁数が 4 の倍数の場合はこれでよいが,桁数を 4 で割って
あまりが 2 の場合,m/2+1 桁目と m/2 桁目が残る.
ところが
am/2+1 = am/2
であるので,
am/2+1・10m/2+1 + am/2・10m/2
= am/2・11・10m/2
となり,余った m/2+1 桁目と m/2 桁目 も 11 で割り切れ、
よって回文となっている偶数桁の整数は必ず 11 で割り切れる.

(ペンネ−ム:wasmath)
偶数桁の回文的自然数Nは
N = a0・102n-1+a1・102n-2+a2・102n-3+・・・ +an-1・10n+an-1・10n-1+・・・+a1・10+a0と表されます。
証明1)
2m桁の数M(2m)=111・・・1=11+1100+110000+・・・+110・・・0
が11の倍数であることに注意すると,
N=a0・M(2n)+10(a1-a0)・M(2n-2) +100(a2-a1)・M(2n-4)+・・・ +10n-1・{an-1-an-2}・M(2)は11の倍数となります。
証明2)
102m-1+1=(10+1)・{ 102m-2-102m-3+102m-4-・・・
・・・+100-10+1) が11の倍数であることに注意すると,
N=a0・{ 102n-1+1 } + 10・a1・{ 102n-3+1 } +・・・ + 10n-1・an-1・(10+1)は11の倍数となります。
コメント1)
11と10は互いに素ですから,
Nが11の倍数 ⇔ 10Nが11の倍数
が成り立つので,添字が見づらければNの代わりに10n・Nが
11の倍数であることを示す手もあります。

(ペンネ−ム:kiyo)
ある数が11の倍数かどうかの早見法は既知とします。
即ち、
この問題は回文数で偶数桁であるから、この回文数の偶数桁の和と奇数桁の和との 差は0となります。
「ある自然数の偶数桁の和と奇数桁の和との差が11の倍数のとき、 ある自然数は11の倍数となる。」

(ペンネ−ム:水の流れ)
2n桁の回文数を10進法で
anx2n―1+an−1x2n―2
+an−2x2n―3+・・・+a3xn+2
+a2xn+1+a1xn
+a1xn−1+a2xn−2+・・・
+an−1x1+an
=f(x)と表すことができる。
ただし、x=10で、1≦an≦9,0≦an−1,an−2,・・・,a2,a1≦9の自然数とする。
ここで、偶数位の数字の和と奇数位の数字の和の差はが11の倍数のとき、
その数字は11の倍数であると言えるから、
偶数桁の数字の和と奇数桁の数字の和の差を調べると、
f(−1)=−an+an−1−an−2+・・・−an−1+an=0
となり、その数字が11の倍数である判定条件を満たす。
したがって、2n桁の回文数は常に11の倍数である。
終わり
追伸:回文には有名な俳句と和歌があります。
きゆるまた にわのこのはに たまるゆき
なかきよの とおのねふりの みなめざめ なみのりふねの おとのよきかな

(ペンネ−ム:中川 幸一)
まずはじめに、
と言うことを証明します。
11の倍数は『末位から左へ向かって奇数番目のものの和から、偶数 番目のものの和を引いた差が11の倍数になる。』
〈proof〉
| N | =(105)a+(104)b+(103)c+(102)d+10e+f |
| ={(105+1)a+(104-1)b+(103+1)c+(102-1)c+(10+1)e}+ {(b+d+f)-(a+c+e)}+(11の倍数) |
これを用いて計算をすると、
abcdef……fedcba:(a+c+e+……+f+d+b)-(b+d+f+……+e+c+a)=0
となり11の倍数であることが示された。

(ペンネ−ム:Nと〜)
整数が11で割り切れるかどうかは以下のように判断できます。
【定理1】
整数の
一の位+百の位+万の位
十の位+千の位+十万の位
と一桁とばしで数字の値(変な言い回し)を足して、 この二つの和の差が11の倍数であれば元の数は11で割り切れる。
この【定理1】が認められれば、1月の問題は明らか。
【定理1】の証明は、【補題2】を使います。
とかけるから。
Σ(ak×10k) =a1+(99+1)a3+(9999+1)a5+・・・ +(11−1)a2+(1001−1)a4+・・・・ =(11の倍数)+(a1+a3+a5+・・・) −(a2+a4+a6+・・・)
【補題2】の証明は数学的帰納法で出来ます。
【補題2】
10の偶数乗ー1は11で割り切れる。 10の奇数乗+1は11で割り切れる。

(ペンネ−ム:ひょうたん)
まず11で割れる数がどんな数なのかというので補題
左から数えてP番目の桁の数をNpとするとき N1+N3+N5+…+Np-1=N2+N4+N6+…+Np が成立てばその数が11で割れる(pは任意の偶数)
本題
回文の偶数桁の自然数をTとします。
回文なので自然数Tの各位の数は
N1=Np、N2=Np-1、N3=Np-2、…Np/2=Np/2+1
となります。
これより自然数Tに対して
N1+N3+N5+…+Np-1=N2+N4+N6+…+Np
が成立つのでTは11で割りきれます。 Q.E.D
蛇足ですがpを任意の奇数にしても補題は成立ちます。
つまり、
各位の数を1個とばしで足した合計がそれぞれ等しくなれば11で割りきれます。

| kiyo | Junbou | 夜ふかしのつらいおじさん |
| judas | モルモット大臣 | スチューデント |
| d3 | yokodon | 水の流れ |
| BossF | 浜田 明巳 | wasmath |
| とうがらし | T_Tatekawa | 高橋 道広 |
| DDT | teki | こざっぱ |
| Nと〜 | 月の光 | 中川 幸一 |
| ひょうたん |

2002年のスタートにあたって、たくさんの方から解答を寄せていただき、 どうもありがとうございました。
102n+1+1が、11の倍数であるというアプローチの解答が多かったように思います。 この証明には、数学的帰納法、二項展開を用いる、因数分解を用いる などいろいろな方法があると思います。 高橋 道広さんが上手にまとめてくださいました。
ある数の倍数であるということを示すのに剰余(mod)式で考えるというのは、 大変有効ですし、証明を記述する際にもとてもすっきり書けると思います。
とってもユニークだなあと思ったのは、T_Tatekawaとwasmathさんです。 T_Tatekawaさんのアイディアは、上からと下から2桁ずつペアにして足せば 必ず11の倍数になるということだと思います。 wasmathさんの証明1もなかなか おもしろいアイディアだと思います。
11の倍数の判定法
をご存知でしたでしょうか? これを前提にすると証明は簡単ですね。 この判定法そのものの証明は、中川 幸一さん、Nと〜さんがしてください ましたので参考にしてください。
「ある自然数の偶数桁の和と奇数桁の和との差が11の倍数のとき、 ある自然数は11の倍数となる。」

 E-mail
E-mail
 戻る
戻る
 top
top