Weekend Mathematics�^����^���55
�T�T�D�����`�̖��

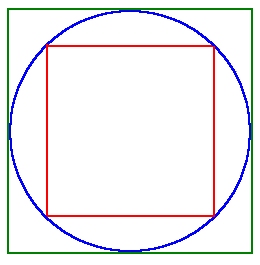
�P�D�~�ɓ��ڂ��鐳���`�̖ʐςƁA���̉~�ɊO�ڂ��鐳���`�̖ʐςƂ̔�����߂Ă��������B
�Q�D(�ȒP������E�E�E�ƌ�������)
���O�p�`��A���܊p�`�A���Z�p�`�ł͂ǂ��ł��傤�B
���w�p�X�������h�^�c���O�Y���^�u�k�Ѓu���[�o�b�N�X
�i�y���l�|���F�؎��j
�Ԑ��̐����`���S�T�x��]���đΊp���������Ă݂�ƁE�E�E�A���A
�O���̗̐����`���S�������Ă��邶��Ȃ��́B����ł���4�������Ă�
����ꂽ�����`��Ԑ������ꂼ��2����1�ɕ����Ă���̂�����A�����A�����Ȃ̂ˁA
�ʐς�2���̂P�Ȃ�I

�i�y���l�|���Fmhayashi�j
�u�~�ƁA����ɓ��ڂ��鐳���`�Ƃ̐ړ_�v��
�u�~�ƁA����ɊO�ڂ��鐳���`�Ƃ̐ړ_�v�Ɛڂ���悤��
�����`����]�������
�i�܂��蕶�̐}�Ō����ƁA�Ԃ������`���S�T�x��]������Ɓj�A
���炩�ɖʐϔ�͂P�F�Q�ƂȂ�B

�i�y���l�|���F��Ȃ� �j
���ڂ���~�̔��a���q�Ƃ����
���̉~�ɊO�ڂ��鐳���`�̂P�ӂ̒����� �Q�q�ɂȂ�܂��B
����Ă��̐����`�̖ʐς͂Q�q�~�Q�q���S�q�Q�ł���ˁB
���ɂ��̉~�ɓ��ڂ��鐳���`�̂P�ӂ̒�����
�O�p�`�̒藝����Q�q�����[�g�Q �ɂȂ�܂��B
�ʐς́i�Q�q�����[�g�Q�j �~�i�Q�q�����[�g�Q�j ���S�q�Q ���Q���Q�q�Q
�ق�ł����� �O�ڂ��鐳���`���Q�œ��ڂ��鐳���`���P�łQ�F�P�������ł��B

�i�y���l�|���F�C�V��j
�~�ɓ��ڂ��鐳���`�͐����`�̑Ίp���Ɖ~�̒��a�������ł�������
�c���Q�q�Ƃ���Ɠ��ڂ��鐳���`�̂P�ӂ̒�����
�P�ӁF�P�ӁF�Ίp�����P�F�P�F��Q���
�P�F��Q���w�F�Q�q�@���@�w�E��Q���Q�q�@���@�ӂw���q�E��Q
����ē��ڂ��鐳���`�̖ʐς�
�w�E�w���Q�E�q�Q�@�ƂȂ�B
�~�ɊO�ڂ��鐳���`�̂P�ӂƉ~�̒��a�͓����ł�������
�x�E�x���Q�q�E�Q�q���S�E�q�Q�@�ƂȂ�B
��L���@���ڂ��鐳���`�F�O�ڂ��鐳���`��
�Q�E�q�Q�F�S�E�q�Q���P�F�Q�ƂȂ�B
�~�ɓ��ڂ��鐳�O�p�`�̏d�_�͉~�̒��S�_�ƂȂ邩��
�O�p�`�̒�ӂ�������ꂽ�����̒����͂Q�F�R���q�F�w���
�w���R�q�^�Q�ƂȂ�B
�������ӂ̒����́�R�F�Q���R�q�^�Q�F�k���
�k�E��R���R�q�@���@�k���q�E��R�ƂȂ�
��������ڂ���O�p�`�̖ʐς�
�i�q�E��R�j�E�i�R�q�^�Q�j�E�i�P�^�Q�j���i�R�E�q�Q�E��R�j�^�S
�~�ɊO�ڂ��鐳�O�p�`�̏d�_�͂��~�̒��S�_�ƂȂ邩��
�O�p�`�̒�ӂ�������ꂽ�����̒����͂P�F�R���q�F�w���
�w���R�q�ƂȂ�
�������ӂ̒����́�R�F�Q���R�q�F�k���
�k���Q�q�E��R�ƂȂ�B
������O�ڂ���O�p�`�̖ʐς�
�R�q�E�i�Q�q�E��R�j�E�P�^�Q���R�E�q�Q�E��R
��L�����ڂ���O�p�`�F�O�ڂ���O�p�`��
�i�R�E�q�Q�E��R�j�^�S�F�R�E�q�Q�E��R���P�F�S�ƂȂ�B
�~�ɊO�ڂ��鐳�Z�p�`�������傫���̐��O�p�`���U���g�ݍ��킹�����̂ł���B
���̏ꍇ���O�p�`�̒�ӂɑ��鐂���̒������q�ł���B
����ĂQ�F��R���w�F�q�@���@�w���i�Q�q�E��R�j�^�R
������O�p�`�̖ʐς�
�q�E�i�Q�q�E��R�j�^�R�E�P�^�Q���i�q�Q�E��R�j�^�R
�~�ɊO�ڂ��鐳�Z�p�`�͂�����U�{�������̂ƂȂ�B
��L�����ڂ���Z�p�`�F�O�ڂ���Z�p�`��
�i�q�Q�E��R�j�^�S�F�i�q�Q�E��R�j�^�R���R�F�S�ƂȂ�B

�i�y���l�|���Fkiyo�j
���m�p�`�̂Ƃ��A
������@COS(180/N) �F�P
�ʐϔ�@COS�Q(180/N)�F�P
�m���S�̂Ƃ��@�@�@�@�@�@�@�@�@�@�@�@�@�P/�Q�F�P���P�F�Q
�m���R�̂Ƃ��@�@�@�@�@�@�@�@�@�@�@�@�@�P/�S�F�P���P�F�S
�E�E�E
�m��8110�̂Ƃ��@ .9999998
�m��8111�̂Ƃ��@ .9999998
�m��8112�̂Ƃ��@ .9999999
�m��8113�̂Ƃ��@ .9999999
���W�P�P�Q�p�`�łقڂP�B
�@�@

�i�y���l�|���F�a�������e�j
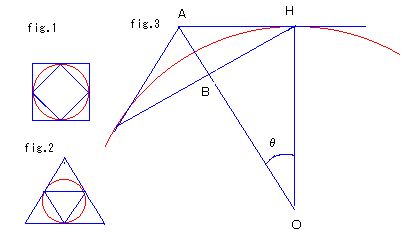
fig.1,2��薾�炩�ɐ����`�ł�2�F1�A
���O�p�`�ł�4�F1�ł�
n�p�`�̏ꍇfig3�̗l�ɓ_���惊�A�~�̔��a��r�Ƃ����
AH=r tan�Ɓ@�@BH=r sin�� ������
������́@tan��:sin��=1:cos��
�����Ėʐϔ�́@1�Fcos2��
(�������@��=��/n)

�i�y���l�|���F�c�c�s�j
�����p�`�̂ق��ł����܂��B
�m���j�n
�����p�`�Ɖ~�Ȃ̂ŁA�Ⴆ�ΐ��R�p�`�ōl������イ�Ԃ�B
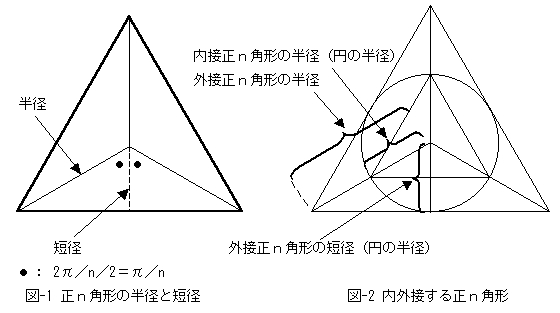
�}-1�̂悤�ɁA�����p�`�̒��S�i�d�S�j���璸�_�܂ł̋����𐳂��p�`�̔��a�C
�����p�`�̒��S����ӂ܂ł̐���������Z�a�ƁA�i����Ɂj��`���܂��B
��������Ƒ�ӂ��A���a�ƒZ�a�̓����������p�`�̖ʐϔ�����߂�A�Ƃ����Ӗ��ɂȂ�B
�m���s�n
�@ �}-1���A�O�ڔ��a�ƊO�ڒZ�a�̔�́Acos(��/n)�D
�A �}-2���A���ڔ��a�͊O�ڒZ�a�ɓ������D
�B ����āA�O�ڔ��a�Ɠ��ڔ��a�̔��cos ��/n�ŁA�ʐϔ��cos2(��/n)�D
�@�@�����D�i���ڐ����p�`�̖ʐρj�^�i�O�ڐ����p�`�̖ʐρj��cos2(��/n)

�i�y���l�|���F����j
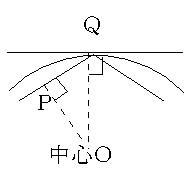
���}�̂悤�ɉ~�ɓ��ڂ��鐳���p�`�̒��_�ƊO�ڂ��鐳���p�`�Ɖ~�̐ړ_���d�˂�B
���ڂ��鐳���p�`�̖ʐςƊO�ڂ��鐳���p�`�̖ʐϔ��
���S�n���e�����p�`�ɉ��낵�������ƌ����_���o�C�p�Ƃ����
�b�n�o �b�Q�F�b�n�p�b�Q�ƂȂ�B
�����ŁA�ڂo�n�p���R�U�O���^�Q�����P�W�O�^���@������
�b�n�p�b���b�n�o�b�^�������i�P�W�O�^���j
| ���ʐϔ� | ���b�n�o �b�Q�F�b�n�p�b�Q |
| ���b�n�o �b�Q�F�i�b�n�o�b�^�������i�P�W�O���^���j�j�Q | |
| ���P�F�P�^�������Q �i�P�W�O���^���j |
�����ŁA�����`�̏ꍇ��
| �ʐϔ� | ���P�F�P�^�������Q �i�P�W�O���^�S�j |
| ���P�F�P�^�������Q�S�T�� | |
| ���P�F�i��Q�j�Q���P�F�Q |
���O�p�`�̏ꍇ��
| �ʐϔ� | ���P�F�P�^�������Q �i�P�W�O���^�R�j |
| ���P�F�P�^�������Q�U�O�� | |
| ���P�F�Q�Q���P�F�S |
���܊p�`�̏ꍇ��
| �ʐϔ� | ���P�F�P�^�������Q �i�P�W�O���^�T�j |
| ���P�F�P�^�������Q�R�U�� | |
| ���������Q�R�U���F�P |
���Z�p�`�̏ꍇ��
| �ʐϔ� | ���P�F�P�^�������Q �i�P�W�O���^�U�j |
| ���P�F�P�^�������Q�R�O�� | |
| ���P�F�i�Q�^��R�j�Q���R�F�S |

�i�y���l�|���Fyokodon�j
�i1�j
�~�̔��a�� R �Ƃ���B
���ڂ��鐳���`�̈�ӂ̒����� 21/2�~R�B
�O�ڂ��鐳���`�̈�ӂ̒����� 2R �B
�Ȃ̂ŁA�e�X�̖ʐς́A���ڂ��鐳���`�� 2R2 �A�O�ڂ��鐳���`�� 4R2 �B
����āA�ʐϔ�́A�i�O�ځj�F�i���ځj��2�F1�B
�i2�j
��ʂ̐����p�`�̏ꍇ�ɂ��čl����B
���ڂ��镪�Ɋւ��ẮA�����p�`�̈�ӂƊO�ډ~�i���a R�j�̒��S�����ӎO
�p�`�Ɋւ��āA
��ӂ̒����� 2Rsin(��/n)�A������ Rcos(��/n)
����āA���ڂ��鐳���p�`�̖ʐςr�́A
n�~{(���)�~(����)}/2�� nR2�~sin(��/n)cos(��/n)
�O�ڂ��镪�Ɋւ��Ă����l�ɍl���āA�O�p�`��������
��ӂ̒����� 2Rtan(��/n)�A������ R
����āA�O�ڂ��鐳���p�`�̖ʐςs�́A
n�~{(���)�~(����)}/2�� nR2�~tan(��/n)
�ȏ���A
| �r�F�s | ��sin(��/n)cos(��/n)�Ftan(��/n) |
| ��cos2(��/n)�F�P |

�i�y���l�|���F�˂��j
�P�D
���ڐ����`���S�T�x�X���A�O�ڐ����`�̊e�ӂ̒��_�ɒ��_������悤�ɂ���Ƃ킩��
�₷���B
���炩�ɁA�ʐϔ�͂P�F�Q�B
�Q�D
�P�Ɠ����悤�ɁA�O�ڑ��p�`�̊e�ӂ̒��_�_�Ƃ������p�`���l����悢�B
�~�̒��S���n�Ƃ��A��������A
�O�ڑ��p�`�̒��_�܂ł̒��������A
���ڑ��p�`�̒��_�܂ł̒������O�ڑ��p�`�̕ӂ̒��_�܂ł̒��������A
���ڑ��p�`�̕ӂ̒��_�܂ł̒�������
�Ƃ���B���S�p�������^���Ƃ���B
���ڑ��p�`�̖ʐςr�P�́A�r�P����(1/2)���� ��������
�O�ڑ��p�`�̖ʐςr�Q�́A�r�Q��n(1/2)���� ��������
���҂̔�́A�r�P�F�r�Q�����F��
�ƂȂ�B
�����ŁA������ ���������A������ ���������ƌ����W����A
�r�P�F�r�Q��������2 ���F�P
��������2 �i�^���j�F�P�ƂȂ�B
�����p���āA
�����R�E�E�E������2�i�^�R�j�F�P���i�P�^�Q�j2�F�P���P�F�S
�����S�E�E�E������2�i�^�S�j�F�P���i�P�^��Q�j2�F�P���P�F�Q
�����T�E�E�E������2�i�^�T�j�F�P���i�P�{��T�^�S�j2�F�P���R�{��T�F�W
�����U�E�E�E������2�i�^�U�j�F�P���i��R�^�Q�j2�F�P���R�F�S

�i�y���l�|���F���� ���L�j
����̖��͂P�͏u�E�ł��B�~�̒��S�𒆐S�ɂ���45�x��]�����ďI���B1:2��
���B
�Q�͐}�̂悤�ɍl�����,��n�p�`��2n��������ƎO�p�`BOC�ƎO�p�`AOB�̖ʐϔ��
���ׂ�Ɨǂ����ƂɂȂ�܂��B���̎O�p�`�͑����ł�����
OB=1�@�pAOB=���Ƃ����,�@�������OC:OB=cosx:1�@���
�ʐϔ�́@(cosx)2:1�@x=2��/2n=��/n
n=3�̂Ƃ��@cos��/3=1/2���@1/4:1=1:4
n=4�̂Ƃ��@cos��/4=1/��2���@1/2:1=1:2
�����܂ł͐}�������ق��������ł��ˁB���ɁA
n=6�̂Ƃ�cos��/6=��3/2���@3/4�@
����́A���s���̕⏕�����������Ƃɂ���đ�������ʐϔ���������Ƃ��ł��܂�
�ˁB
n=5�̂Ƃ��@cos��/5��2�{�p3�{�p�𗘗p���邩,36�x72�x72�x�̎O�p�`�̊p��2������
���g����,��5�p�`�̑Ίp���łł���}�`�̑������g�����c
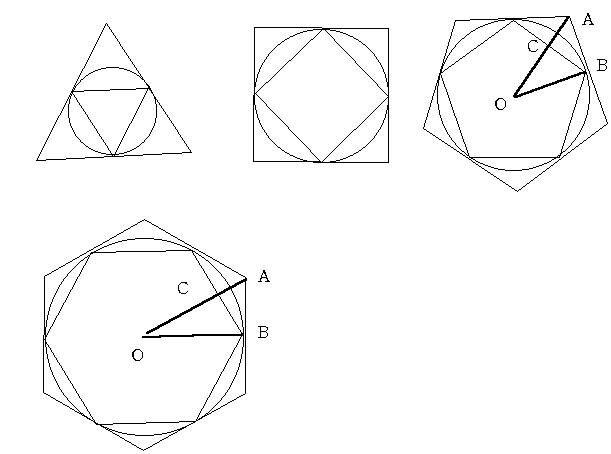

�i�y���l�|���F�l�c�@�����j
�����p�`�ɂ��čl����D
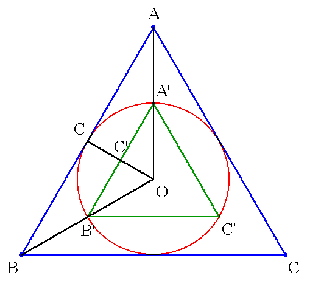
�}�ɂ����āC���`'�n�b'�䁢�`�n�b�ł��邩��C�������
| �b'�n�F�b�n | ���b'�n�F�`'�n��cos�ڂ`'�n�b'�F�P |
| ��cos�ڂ`�n�b�F�P��cos(�Q�^�Q��)�F�P | |
| ��cos(�^��)�F�P |
���O�p�`�̏ꍇ�C
�@�@{�P�{cos(�Q�^�R)}�F�Q���P�F�S
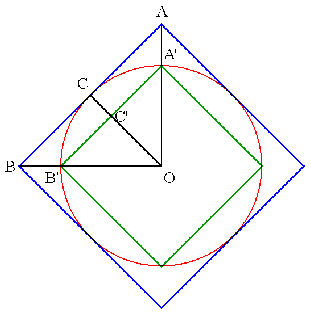
�����`�̏ꍇ�i���P�̓��j�C
�@�@{�P�{cos(�^�Q)}�F�Q���P�F�Q
���܊p�`�̏ꍇ�C
�@�@{�P�{cos(�Q�^�T)}�F�Q��(�R�{��T)�F�W
���Z�p�`�̏ꍇ�C
�@�@{�P�{cos(�^�R)}�F�Q���R�F�S
�����p�`�̏ꍇ�C
�@�@{�P�{cos(�Q�^�V)}�F�Q
�����p�`�̏ꍇ�C
�@�@{�P�{cos(�^�S)}�F�Q��(�P�{��Q)�F�Q��Q

�i�y���l�|���F��ӂ����̂炢�������� �j
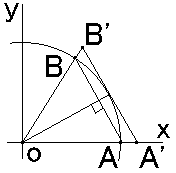
�P�@�����͂P�F�Q�ł��B�i�����`�̏ꍇ�j
�Q�@�~�ɓ��ڂ��鐳���p�`�ƊO�ڂ��鐳���p�`�̖ʐς̔�́A
�P�F�P�^cos2(�^��)�ł��B
���a�P�̉~�ɁA������ɒ��_������悤�ɂQ�̐����p�`�����ڂƊO�ڂ����Ă���Ƃ��܂��B
������̒��_���`�A�`�f�Ƃ��܂��B�����Ɏ��̒��_���a�C�a�f�Ƃ��܂��B
�����p�`�͊e���_�𒆐S�ƌ��ԂƂ��̓ӎO�p�`���ł��܂��B
�Q�̐����p�`�̖ʐς̔�́A���̂Q�̓ӎO�p�`�̖ʐς̔�Ɠ����ł��B
�܂��A�����̐}�`�̖ʐς͑Ή����钷���̂Q��ɔ�Ⴕ�܂��B
�����Ō��_���琳���p�`�̕ӂ܂ł̋��������߂ĂQ�悵�܂��B
�O�ڂ��鐳���p�`�̕ӂ܂ł̋����͂P�ŊȒP�ł��B
��̐}�Ŋp�`�n�a�̑傫�����A�Ɓi2�^���j�Ƃ��܂��B
�_�`�̍��W�́i�P�C�O�j�A�_�a�̍��W�́icos�ƁCsin�Ɓj�ł��B
�Q�_�`�A�a��ʂ钼���̕������́A
�@�@�@ ���|0��(0�|sin��)�^(1�|cos��)�(���|1)�D
�@��������āA
sin�ƥ���{(1�|cos��)����|sin�Ɓ��O�D
�@���_�Ƃ��̒����̋������́A
| �� | ��sin�Ɓ^sqrt(sin2�Ɓ{(1�|cos��)2) |
| ��sin�Ɓ^sqrt(2(1�|cos��))�D |
| ��2�F�P2 | ��sin2�Ɓ^2(1�|cos��)�F�P |
| ���P�F2(1�|cos��)�^sin2�� �@�y���p��Q�{�p�̌������g���āz | |
| ���P�F2�2sin2(��/�Q)�^�o2 sin(��/�Q)cos(��/�Q)�p2 | |
| ���P�F�P�^cos2(��/�Q) | |
| ���P�F�P�^cos2(�^��)�D |
�����R�̂Ƃ��́A�P�F�S
�����S�̂Ƃ����A�����`�̂Ƃ��ł��B�i�P�F�Q�j
�����T�̂Ƃ��́A�P�F�P�U�^(sqrt(5)�{�P)2�@�@�y��ɐ����z
�����U�̂Ƃ��́A�P�F�S�^�R
�������̂Ƃ��́A�P�F�P�Ɏ������܂��B
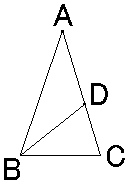
�y��̐����z
�����T�̂Ƃ��́A����cos72�������߂邱�ƂɋA�����܂��B
�E�̐}�̂悤�ɁA�p�`��36���A�p�a���p�b��72���̓ӎO�p�`���l���܂��B
�a�b���a�c�ƂȂ�悤�ɕ⏕���������ƁA���`�a�b�������a�b�c�Ȃ̂ŁA
�`�a���P�A�a�b�����Ƃ���ƁA�P�F�������F(�P�|��)�@�Ȃ̂ŁA
��2�{���|�P���O
����{sqrt(�T)�|�P}�^�Q�@�@�y�����O�z
��cos72����{sqrt(�T)�|�P}�^�S
�����
| cos(��/�Q) | ��cos36����sqrt�o�P�^�Q�E(�P�{cos72��) } |
| ��sqrt{�P�^�Q�E(�P�{(sqrt(5)�|1)�^�S)}�@�@�y�Q�d�������J���āz | |
| ��(sqrt(�T)�{�P)�^�S |

| kiyo | ��ӂ����̂炢�������� | ���� ���L |
| ��Ȃ� | yokodon | �l�c�@���� |
| ���� | �؎� | �˂� |
| �a�������e | DDT | �C�V�� |
| mhayashi |

����̖��́A����̉~�ɓ��ڂ��鐳���p�`�ƊO�ڂ��鐳���p�`�Ƃ̖ʐϔ�����߂���ł����B
�l�p�`�ɂ��ẮA�؎������Amhayashi�����̉̂悤�ɂS�T�x��]������AOK�ł��B
�O�p�`�A�܊p�`�A�Z�p�`�Ƃ��āA�X�ɍl��������A�����p�`�Ƃ��čl���������ĊO�킩��₷�������̂ł͂Ȃ����Ǝv���܂��B
���l���̕��������Ă����������̂ŁA���߂Ă̐����͏ȗ����܂����A���ʂ�cos2(��/n)�F�P�ł��B
kiyo�����̂��w�E�̂悤�ɁA�������̂Ƃ��A���̔�͂P�Ɏ������܂��B
���ڐ����p�`�̖ʐρ��~�̖ʐρ��O�ڐ����p�`�̖ʐ�
�Ƃ������ƂƏƂ炵���킹�čl����A������͂��݂����ɂ��A
���ڐ����p�`�̖ʐρA�~�̖ʐρA�O�ڐ����p�`�̖ʐς́A�Ƃ��ɂ������̂Ƃ�
�����l�r�Ɏ�������Ƃ������Ƃ��킩��܂��B
�����āA���̂��Ƃ���~�����̒l�����܂�킯�ł��B
������V�~�����[�V�����ł���T�C�g���Љ�܂��傤�B
THE UNIVERSITY OF UTAH�@�́@ Archimedes and the Computation of Pi

 E-mail
E-mail
 �߂�
�߂�
 top
top