Weekend Mathematics�^����^���54
�T�S�D�������V���̖��
���M�V���̗����̘r�̒������������Ȃ���A�������͂��邱�Ƃ͂ł��܂���B �������A�����ɂ͗����̘r�̒������Ⴄ�������V����������܂���B �������A�K���Ȃ��Ƃɐ����������͂�����Ă��܂��B
���P
�����̉�����̎M�ɂ̂��A�����ł͂���܂��ƁA�P�P�T�Qg����܂����B ���ɂ��̓����E�̎M�ɂ̂��A�����ł͂���܂��ƁA�P�Q�T�Og�ƂȂ�܂����B ���̓��̉�̐������d���͂�����ł��傤���H
���Q
���̓V�����g���āA�Qkg�̓����͂����Ă��������B
���w�p�X�������h�^�c���O�Y���^�u�k�Ѓu���[�o�b�N�X
�i�y���l�|���Fsho �j
���`���w�ł����A�����̃��[�����g�ōl���܂��i��
�V���̐^�ƍ��̊Ԃ̒�����L�A�E�Ƃ̊Ԃ��q�A���̏d����m�ƒu���ƁA
�k�E�l��1152�E�q�E�E�E�@
�k�E1250���l�E�q�E�E�E�A
�A���R��1250L/M�@��������������M=1200 �E�E�E�E�E��

�i�y���l�|���F���̗���̐\���q�j
���P
�����̓V���̒�����X �E���̓V���̒�����Y�Ƃ������̏d����A�Ƃ����
A�EX���P�P�Q�T�EY�@,�P�Q�T�O�E�w���`�E�x�ƂȂ�̂ŁA�����������
�`�Q�E�x���P�P�Q�T�E�P�Q�T�O�E�x
�`�Q���P�P�Q�T�E�P�Q�T�O
�䂦�Ɂ@�`���P�Q�O�O
����ċ����P�Q�O�O�O����
���Q
���P���w�F�x���Q�S�F�Q�T�ƂȂ�̂ł�����̏d�����s�Ƃ����
���ɓ���u�����Ƃ����
�Q�O�O�O�E�Q�S���Q�T�E�s�@�@����Ăs���P�X�Q�O�i���j
���l�ɉE�ɒu����
�s���Q�O�W�R�A�R�R�R�R�E�E�E�E�E�i���j

�i�y���l�|���Fkiyo�j
�@�x�_����E���̒����i�w�j�A�x�_���獶���̒����i�x�j�Ƃ���B
�����̉���yg�Ƃ���B�Ă��̌������A
�P�j
| �P�P�T�Q�E�w | ���y�E�x |
| �y�E�w | ���P�Q�T�O�E�x |
| �y�Q | ���P�P�T�Q�E�P�Q�T�O |
| �y | ���P�Q�O�O |
�Q�j
�@�@�@�@�w�F�x���Q�T�F�Q�S
�@�@�@���̎M�ɂQ�O�O�Og�������̉�𑪂��悤�ɂ���B
�@�@�@�E�̎M�ɍڂ��镪�����w���Ƃ���B
�@�@�@�Q�O�O�O�E�Q�S���w�E�Q�T
�@�@�@�@�@�@�@�@�@�w���P�X�Q�O
���Ȃ킿�A�E�̎M�ɂP�X�Q�O���̕������ڂ��A
���̎M�ɒނ荇�������̋����̉���ڂ���ƁA
�Q�O�O�O������邱�ƂɂȂ�B
�i�E�̎M�ɋ����̉���ڂ�����@���ƍ��̎M�ɍڂ��镪��������g�ƂȂ�Ȃ��B�j

�i�y���l�|���F�C�V��j
���P
�@�@�@�w�@�@�@�@�@�@�@�@�x
�{�|�|�|�|�|�|�|�|�|�|�|�|�|�|�{
�b�@�@�@�@�@ �@���@ �@�@�@�@�@�b
�P�Q�T�O�@�@�@�@�@�@�@�@�@�@�@���F�y
���F�y�@�@�@�@�@�@�@�@�@�@�P�P�T�Q
���Q
�����P�Ƃ���
�@�@�@�Q�S�@�@�@�@�@�@�@�Q�T
�{�|�|�|�|�|�|�|�|�|�|�|�|�{
�b�@�@�@�@ �@���@�@�@ �@�@�b
�Q�O�O�O�@�@�@�@�@�@�@�@�@�@�w
�x�@�@�@�@�@�@�@�@�@�@�@�Q�O�O�O
�悸�@�Q�O�O�O�E�Q�S���Q�T�E�w
�w���Q�O�O�O�E�Q�S�^�Q�T���W�O�E�Q�S���P�X�Q�O��
���Ɂ@�Q�O�O�O�E�Q�T���Q�S�E�x
�x���Q�O�O�O�E�Q�T�^�Q�S���T�O�O�O�O�^�Q�S���Q�O�W�R���ł���B

�i�y���l�|���F���Îu�j
����F�r�̒����͈���Ă��邪���̏�ԂŒނ荇���Ă���B
�����łȂ��Ƃ����琳���������������Ă��ʂ�Ȃ��i�Ǝv���j
���P
���̏d�������A�x�_���獶�̎M�܂ł̒��������A�E�����Ƃ���
�V���́i�r�̒����j�~�i�d���j���A���E�œ������ꍇ�ɒނ荇���̂�
�i���w�Z�̎��Ɏ����������L��������j
��������
�@�@�@�������P�P�T�Q���@�c���P
�@�@�@�P�Q�T�O���������@�c���Q
�O���A���ꎟ�������Ȃ̂ŁA�����Q�ł͉����Ȃ���
���̏ꍇ���Ƃ��̔䂳����������̂łƂ肠�������̂܂܉�����
�@�@�@���P���@�@�����P�P�T�Q���^��
�@�@�@���Q���@�@�����P�Q�T�O���^��
�@�@�@�P�P�T�Q���^�����P�Q�T�O���^��
�@�@�@�i���^���j�Q���P�Q�T�O�^�P�P�T�Q
�@�@�@�����i�Q�T�^�Q�S�j���@�c���R
���R�����P�ɑ������
�@�@�@�������P�P�T�Q�~�i�Q�T�^�Q�S�j��
�@�@�@�����P�Q�O�O
�@���D���͂P�Q�O�O��
���Q
���ɂ̂�����̂̏d�������A�E�����Ƃ���ƁA
�@�@�@�����������@�c���S
����������ꍇ�ɒނ荇���B
���R�����S�ɑ������
�@�@�@�������i�Q�T�^�Q�S�j����
�@�@�@�����i�Q�T�^�Q�S�j���@�c���T
�V���͕��ʍ��̎M�̏d�����Œ肵�ĉE�̎M�̏d����ς��ėʂ邩��A
�E�̎M�ɓ����̂��A�������ĂQ�����Ƃ���悤�ɍl����ƁA
�@�@�@�����i�Q�T�^�Q�S�j�~�Q�O�O�O
�@�@�@�@���U�Q�T�O�^�R
�@�@�@�@���Q�O�W�R�{�P�^�R
�P�^�R���Ƃ�������������Ζ������ł����A���Ԃ��ł��傤�B
���傤���Ȃ��̂ŁA�V���̍��E�����ւ��čl����ƁA
�@�@�@�Q�O�O�O���i�Q�T�^�Q�S�j��
�@�@�@�����P�X�Q�O
���x�͂��܂������܂����B���������y�������ł��Ƃ͑���܂����B
���D�E�̎M�ɂP�X�Q�O���̕������̂��č��̎M�ɓ����̂���

�i�y���l�|���F�l�c�@�����j
���P�F
���E�̘r�̒��������ꂼ�ꂘ�C���C�����̐������d�����a���Ƃ���ƁC��������C
�a�E�����P�P�T�Q�E���C�P�Q�T�O�E�����a�E��
���a���P�P�T�Q���^�����P�Q�T�O���^���c�c(1)
��(���^��)2���P�Q�T�O�^�P�P�T�Q��(�Q�T�^�Q�S)2
���^�����O����C
�@�@���^�����Q�T�^�Q�S
(1)����C
�@�@�a���P�P�T�Q�E�Q�T�^�Q�S���P�Q�O�O
�̂ɋ����̐������d���͂P�Q�O�O���ł���D
���Q�F
�@���ɂQ�s�̓����̂���ƁC�E�̏d���́C
�@�@�Q�O�O�O�E���^�����Q�O�O�O�E�Q�S�^�Q�T���P�X�Q�O�i���j
�@�E�ɂQ�s�̓����̂���ƁC���̏d���́C
�@�@�Q�O�O�O�E���^�����Q�O�O�O�E�Q�T�^�Q�S���U�Q�T�O�^�R�i���j
�@�̂ɍ��ɂ̂��C�E�̏d�����P�X�Q�O���ɂȂ�悤�ɂ͂���悢�D

�i�y���l�|���F����j
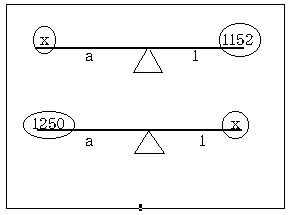
���P�̉�
�E�}�̂悤�ɁA�V���̉E�r�̒������P�A���r�̒�������
�������P�P�T�Q�E�P
�P�Q�T�O�������E�P
�㎮��肁����������
���Q���P�P�T�Q�E�P�Q�T�O
�������P�Q�O�O�@�@
����āA�����̉�̏d���͂P�Q�O�O��
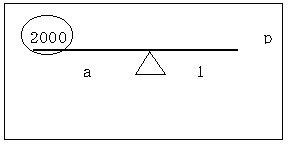
���Q�̉�
�����̏d�������i���j�Ƃ����
���P�̉��
�����P�P�T�Q�^�P�Q�O�O
���Q�O�O�O�������E�P
�������P�P�T�Q�^�P�Q�O�O�E�Q�O�O�O���P�X�Q�O
����āA�Q�L���O�����̓��̉���v��Ƃ�ɂ́A�E�̎M��
�P�X�Q�O�O�����̕����������āA���̎M�ɓ��������Ă肠��
���̓��̏d�����Q�L���O�����ɂȂ�܂��B

�i�y���l�|���Fshino�j
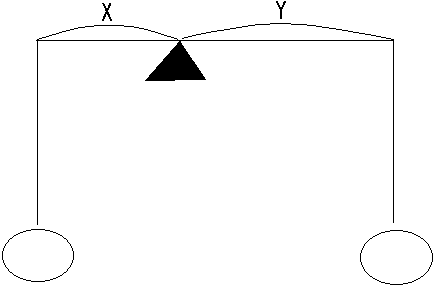
��1
�E�̐}�ŁA���E���肠�����Ƃ���ƁA
�E�̏d���F���̏d��=Y�FX
�����̏d�����hZ�h�Ƃ���ƁA
Y�FX=Z�F1125=1250�FZ
Z2��1440000
��Z��1200
A������1200�O����
��2
Y�FX��1250�F1200
Y�FX��25�F24
������2000�O�����̓����̂��A�E����W�O�����̕������̂���Ƃ���ƁA
25�F24��2000�FW
��W��1920
A�E����1920�O�����̕������̂��A�����ɓ����̂��āA
�肠������A���̏d����2�L���O�����ł��B

�i�y���l�|���FTAKAYA �j
�V���̍��r��a�A�E�r�����A����x�Ƃ��܂��B�ia,b,x�Ƃ����̐����j
���R�A�@1152a=bx�E�E�E�@
�@�@�@�@�@ax=1250b
�������܂��B
������������ƁA�@1152a2=1250b2
�@
�@�@�@�@�@�@�@�@�@�@�@1152=32�27
�@
�@�@�@�@�@�@�@�@�@�@�@1250=54�2
�Ȃ̂Ł@a:b=25:24�������܂��B
�����Ŗ��ɂȂ�͓̂V���̘r�̔�Ȃ̂�a��25�Ab��24�Ƃ��������ɂ��Ă��S�R�\��Ȃ��킯�ł��B
�i������₷���̂ł��̒����ŁB�j
����Ƈ@�́A1152�25=24�x�ƂȂ�
�@�@�@�@�@�@�@�@x=1200
����1200g�ł��B
2000g���v��ꍇ�A�@�̂���2000�ɂ���Ώd���1920g�B
�v�Z�͗v��Ȃ��ł��傤�B

�i�y���l�|���F�p�R�j
Question #1
Suppose L and R are the length of the left and right arms of the balance
and x is the weight of meat, one may get two equations;
x*L=1152*R ...(1) and x*R=1250*L... (2).
Multiply both sides in (1) and (2), then one may get;
x2=1152*1250=(1200)2.
Therefore x=1200 (g).
Question #2
Since 1200*R=1250*L, L/R=1200/1250=0.96.
Therefore a load of 2000 g must be scaled to be 2000*0.96=1920 g
when it is put on the left pan.

�i�y���l�|���F�˂��j
���P
���̘r�̒��������A�E�̘r�̒��������A���̏d�������Ƃ���B
���[�����g���������Ƃ����ނ荇���̏������A
�P�P�T�Q��������
�P�Q�T�O��������
�ӁX�|���Z����
�P�S�S�O�O�O�O�������������Q
����������
�����P�Q�O�O�i���j
���Q
���P���A���Ƃ��̔��
���^�����O�D�X�U�ƕ�����B
�����̏d�������Ƃ���B
�i���j�����E�̂���ɏ悹��ꍇ
�Q�O�O�O�����O�D�X�U����
�����Q�O�O�O�^�O�D�X�U���Q�O�W�R�D�R�R�R�E�E�E�ƂȂ�A�s�K�B
�i�����j�������̂���ɏ悹��ꍇ
�Q�O�O�O�~�O�D�X�U��������
�����Q�O�O�O�~�O�D�X�U���P�X�Q�O
�ƂȂ�A�ʂ邱�Ƃ��ł���B

�i�y���l�|���F�c�c�s �j
�����ēD�܂݂�ł���Ă݂܂��B
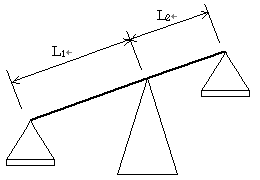
�m���P�n
���̏���
w0�F �{���̏d���i���m���j
w1�F ���Ōv�����Ƃ��݂̂����̏d���i���m���C��1152g�j
w2�F �E�Ōv�����Ƃ��݂̂����̏d���i���m���C��1250g�j
L1�F �V���̍��r�̒����i���m���j
L2�F �V���̉E�r�̒����i���m���j
�x�_�Ɋւ���Ӱ��Ă̒ނ荇�����A
w0 L1��w1 L2 (1)
w2 L1��w0 L2 (2)
����
�@ ���m���͂R�Ȃ̂ɁA�������͂Q�{�����Ȃ��B
��ʘ_�Ƃ��Ă͕s����ŁA���m����w0�CL1�CL2�����̂P���A�Ɨ��ȃp�����[�^�[�Ƃ��đI�ׂ�B
�A w0��Ɨ��ȃp�����[�^�[�Ƃ��đI�ԂƁA�C�ӂ�w0�ɑ���L1��L2�́A
��(1)�C(2)�����Ȃ���Aw0�̕ω��ɍ��킹�ĕω�����B
�B �ɂ��ւ�炸�Aw0�͒�܂�Ƃ����B�Ƃ������Ƃ́Aw0��L1��L2�̒l�Ƃ͖��W�ɒ�܂�B
�܂�L1�CL2��w0�Ɋ��W�͂Ȃ��B
���j
�@ L1�CL2��w0�Ɋ��W���Ȃ����Ƃ����邽�߂ɂ́A��������@���g���āA
L1��L2��w0�ŕ\�����Ƃ���w�͂�����Ηǂ��͂����B
�A �ł�L1�CL2��w0�Ɋ��W�͂Ȃ��̂�����A���̉ߒ���L1��L2�͏����邾�낤�B
�����łȂ���A���W�����Ă��܂��B
�B L1��L2�����������ɂ́A���m����w0�����c��Ȃ�����A���̊W����w0���萔��
�����B�ꂽ���W�ɉ�����ɈႢ�Ȃ��B
���s
(1)���L1�� w0��L2�ŕ\���B
L1��w1�^w0�EL2 (3)
(3)��(2)�ɑ�����Ă�L1�������AL2�ɑ���w0�̕\�������߂悤�Ƃ���B
| w2 L1 | ��w0 L2 |
| w2�Ew1�^w0�EL2 | ��w0 L2 |
| w2�Ew1�^w0 | ��w0 |
| w02 | ��w1 w2 |
| w0 | ��(w1 w2)1/2 |
| w0 | ��(1152�~1250)1/2 |
| ��1200 g |

�i�y���l�|���F���� ���L�j
����́A���ɂ͂܂��Ă��܂����B�Ƃ����̂́A�V���ɏd����������,�ŏ��͌X��
�Ă���Ɖ��肵�Ă����̂ł��B�������A����ł͏����s���łł��Ȃ��悤�ł��B
�ł��Ȃ����́A�������ق����Ēu���āA���Ԃ��\������Ƃ��ɍl����悤�ɂ��Ă�
�܂��B
�@�ŁA�����l���܂����B�V���̏d���͖����A�܂��́A�r�̒������������͂Ȃ����A��
�̏�ŁA�肠���Ă���Ɖ��肵�ĉ����܂����B
���P
���̏d�����w�Ƃ���ƁAX:1152=1250:X�@���@�w=1200
����̖��͑��敽�ς̗�ɂȂ�܂��ˁB���敽�ς̗�ł�
�u�����Ƃ̔��オ�A1�N�ڂ͑O�N��2�{�A2�N�ڂ͑O�N��8�{�A�ł͕��ς́H�v�Ȃǂ�
�������̂�����܂��ˁB
���a���ς́A�u�����Ԃ��s���͎���60km,�A��͎���40km�@���ς�
?�v���Ȃ��B
����̒�R�̎�����Y�̏œ_�����̎�1/f=1/a+1/b�����a���ς̂ɂ��������܂�
���A���̕ӂ̂�����͂Ȃ��ł��傤���B
�Ƃ���ŁA�V���́A�m���A�������ڂ���ق������܂��Ă���͂��ł��ˁB
�Ȃ��ł��傤�B�K�т邩��H�H
���Q
���P
1250:1200=25:24��荶��2000����u���ƁA�E�ɂ́A2000*24/25=1920g�̕�����u���Ƃ肠���̂�
1920���̕������E�ɂ����Ă肠���悤�ɓ���u���Ƃ����悤�ł��B
���Q
25:24=2100:2016����A����2100���̕����A�E��2000���̓���16���̕�����������
�肠���܂��ˁB�Ƃ����炽������̕��@������܂��ˁB
��3
���P������������3920g�̓���,�s�ލ����ȓV���ł肠���悤�ɕ���
��B����́A�ŏ������������ŁA2000���������ł͂Ȃ����Bm(__)m

�i�y���l�|���F��ӂ����̂炢�������� �j
���P
�������d���́A�P�Q�O�O���ł��B
���̏d�����w���A���̘r�̒������k�A�E�̘r�̒������q�Ƃ���ƁA���[�����g���l����āA
�@�@�w�k���P�P�T�Q�q
�@�@�P�Q�T�O�k���w�q
���ꂼ��̕ӂŏ�̎������̎��Ŋ���i�w�A�k�A�q�͂O�łȂ��j�A��������ƁA
�w2���P�P�T�Q�E�P�Q�T�O�D
�@���w���P�Q�O�O���i���O�j
�@�Ȃ��A�k�F�q���Q�S�F�Q�T�ł��B
���Q

�i�y���l�|���FIdaho Potate�j
���1
����́u���敽�ρv�Ƃ�����ł���(^^)�B
���E�̘r�̒����̔�� r : 1 �A����̎��ʂ� M �Ƃ��܂��B
���ɓ���A�E�Ɏ��� m1�̕�����u���Ă肠�����Ƃ���ƁA
M * r = m1 ��� M = m1 / r
�ł��B�܂��A�E�ɓ���A���Ɏ��� m2�̕����ł肠������A
m2 * r = M
�ƂȂ�܂��B�����2�����A
M2 = m1 * m2
���Ȃ킿
M = sqrt( m1 * m2 )
�ƂȂ�܂��B���ł� m1 = 1152 �A m2 = 1250 (g) �Ȃ̂ŁA
M = sqrt( 1152 * 1250 ) = 1200 (g)
�������B
���2
���̎M�� 2kg �̕������̂��A�E�̎M�ɕ�����u���Ă肠�킹��B
�����āA���̎M�̕��������ɒu��������B
���ǁA r �̒l�͂킩��Ȃ��Ă������͏o��A�Ƃ����Ƃ��낪�~�\�ł��ˁB
���Ȃ݂ɁA���1�̌��ʂ���A r = 0.96 �ł��邱�Ƃ��킩��܂��B

| kiyo | �l�c�@���� | ��ӂ����̂炢�������� |
| DDT | ���� | sho |
| shino | �C�V�� | ���� ���L |
| �˂� | �p�R | TAKAYA |
| ���Îu | ���̗���̐\���q | Idaho Potate |

�ނ������������ƃ��[�����g�A���w�Z����ɏK�����Ă��̌���(�Ƃ������V�[�\�[�̌���)�A
�V���̘r�̒����Ƃ�����̏d���̐ς����Ƃ������Ƃł��B
���ɏ悹���ꍇ�ƉE�ɏ悹���ꍇ�̕��ς��Ƃ�����A���̏ꍇ�̕��ς����敽���Ƃ����킯�ł��B
���ςƌ����Ă����낢�날��܂��B
�Q�̐��@a�Ab �ɑ��āA
�������ρE�E�E(a+b)/2
���敽�ρE�E�E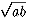
���a���ρE�E�E2ab/(a+b)�@�@[2/c=1/a+1/b]�@�@�@(�����A7/7)
���̂�����̂��Ƃɂ��āA
���� ���L�������R�����g���Ă��������܂����B
�Q�Ԃɂ��ẮAIdaho Potate�����A
��ӂ����̂炢�����������������������������@�ł��ƁA
�g�������̏d����m��K�v�͂���܂���I�I

 E-mail
E-mail
 �߂�
�߂�
 top
top