Weekend Mathematics�^����^���51
�T�P�D�q���̖��
�Q�G�[�J�[�̖q��ɂX���̋�����q����ƁA�P�U���Ŗq����H�אs�����܂��B �܂��A�R�G�[�J�[�̖q��ɂP�W���̋�����q����ƁA�P�O���Ŗq����H�אs�����܂��B
�ł́A�T�G�[�J�[�̖q��ɂR�T���̋�����q����ƁA�����Ŗq����H�אs�����ł��傤���H
�������A�P�ʖʐςɂ��āA���q�O�̖q���̗ʁA�P���ɐL�т�q���̗ʂ͓����ŁA�܂��A �ǂ̋����P���ɓ����ʂ̖q����H�ׂ���̂Ƃ��܂��B
���w�p�Y���^���c�_�^���o�o��
�i�y���l�|���F�C�V��j
�q���̒����F�w�A�P���̐L�сF�x�A�H�ׂ�ʁF�y
�Q�i�w�{�P�U�x�j�|�X�~�P�U�~�y���O�@�@�@�@�@�@�Q�w�{�R�Q�x�|�P�S�S�y���O
�R�i�w�{�P�O�x�j�|�P�W�~�P�O�~�y���O�@�A�@�@�@�R�w�{�R�O�x�|�P�W�O�y���O
�w�{�P�U�x�|�V�Q�y���O�@�@�@�f
�w�{�P�O�x�|�U�O�y���O�@�@�A�f
�@�f�A�A�f���@�@�w���Q�O�x�@�@�y��(1/2)�x�ƂȂ�
�T�i�w�{���x�j�|�R�T�~���~�y���O�@��L�̓�����������
�S�O�x�{�Q���x�|�V���x���O
�x�͋��ʂŏ�������B
�T�����S�O
�����W
����ĂW���ŐH�אs�����B

�i�y���l�|���F���Îu�j
�����P�F�Q�G�[�J�[�ɋ��X���c�P�U��
�����Q�F�R�G�[�J�[�ɋ��P�W���c�P�O��
�P�G�[�J�[������ōl����ƁA
�@���߂̗ʂ��@�@��
�@�P���̐L�т��@��
�@���P��������P���ŐH�ׂ�ʂ��@��
�Ƃ��āA�����P����
�@�@�@���{�P�U�i���j�~���@���@�S�D�T�i���^�G�[�J�[�j�~�P�U�i���j�~��
�����Q����
�@�@�@���{�P�O�i���j�~���@���@�@�@�U�i���^�G�[�J�[�j�~�P�O�i���j�~��
�@�@���{�P�U�����V�Q���@�c���P
�@�@���{�P�O�����U�O���@�c���Q
���P�C�Q���
�@�@�����S�O���@�c���R
�@�@�����@�Q���@�c���S
���́@�T�G�[�J�[�ɋ��R�T���ŐH�אs��������������
�H�אs�����������c�Ƃ���ƁA
�@�@�@���~�T�i�G�[�J�[�j�{�c�i���j�~���~�T�i�G�[�J�[�j���R�T�i���j�~�c�i���j�~��
�@�@�@�T���{�T���c���R�T���c�@�c���T
������c�����߂�����ɂȂ�B�����ŁA���T�ɁA���R�C�S���������
�@�@�T�~�S�O���{�T�~�Q���~�c���R�T���c
�@�@�Q�O�O���{�P�O���c���R�T���c�@�c���U
�����ŁA�����O�͑�ӂ�莩���ł��邽�߁A���U�̗��ӂ����Ŋ���
�@�@�Q�O�O�{�P�O�c���R�T�c
�@�@�c���W
�ȏ���A�u�W���ŁA�H�אs�����v�@�c��

�i�y���l�|���Fjudas�j
1�G�[�J�[������Ɉ���Ő����Ă���ʂ�a�A
��1����1���ŐH�ׂ�ʂ�b�A
���q����O�ɂP�G�[�J�[������ɐ����Ă���q���̗ʂ�c�Ƃ��܂��B
����ƁA
2�~16�~a+2�~c=16�~9�~b�@�E�E�E�@
3�~10�~a+3�~c=18�~10�~b�@�E�E�E�A
�������܂��B�@�̎���3/2�{���ćA�������܂��B�i2�~�@-�A�j
����ƁA
18a=36b�@�@��a=2b
������@�ɑ������
64a+2c=144b�@�@��c=40b
���̓�����d�Ƃ���ƁA
5�~d�~a+5�~c=d�~35�~b
����ɑ�������
5�~d�~2b+5�~40b=d�~35�~b�@10bd+200b=35bd�@25bd=200b�@��d=8
���������āA�W���ŋ��͖q����H�אs�����܂��B

�i�y���l�|���F�˂��j
���������Ƃ���ƁA�q���̗ʁi�f(��)�j��
�ʐρi�r�j�ɔ�Ⴕ�đ����i���萔�o[�q���̗ʁ^ac�Eday]�j�A
���̓����i�b�j�ɔ�Ⴕ�Č���i���萔�p[�q���̗ʁ^���Eday]�j�B
�ŏ��̖q���̗ʁi�f(�O)�j�͖ʐρi�r�j�ɔ�Ⴗ��i���萔�q[�q���̗ʁ^ac]�j�B
��̏�����藧�������
�f(��)���q�r�{�o�r���|�p�b��
�����A
�O���Q�q�{�R�Q�o�|�P�S�S�p
�O���R�q�{�R�O�o�|�P�W�O�p
��̎����
�o���Q�p
�q���Q�O�o���S�O�p
�ƕ�����B�ŏ��̎������������āA
| �f(��) | ���S�O�p�r�{�Q�p�r���|�p�b�� |
| ���p�i�S�O�r�{�Q�r���|�b���j |

�i�y���l�|���F���̗��� �j
���@�P�G�[�J�[������ŏ��ɁA�q�����@���@�̗ʁ@���������Ă����Ƃ���B
���@�P�G�[�J�[�����薈���A�q�����@���̗ʁ@�����L�тĂ���Ƃ��܂��B
���@���P���������A�q�����@���̗ʁ@�����H�ׂ�Ƃ��܂��B
�����ŁA���߂�������@�����@�Ƃ��āA�����������ƁA
�Q���{�Q�~�P�U�����X�~�P�U���@�c�c�@
�R���{�R�~�P�O�����P�W�~�P�O���@�c�c�A
�T���{�T�~�������R�T�~�����@�c�c�B
�@�C�A�@����@�����Q���@�A�����S�O���@
������B�ɑ�����ā@�����W�@�@�@����āA�@�W���i���j

�i�y���l�|���Ftemutin�j
| ���q���́A�q���̎��n�\�� | �w(kg/ac) |
| ���������̖q�������� | ���w(kg/ac/d) |
| �P���̋��������q���̗� | �x(kg/h/d)�@�@h=��(���P���̂���) |
| ���߂���� | �y(d) |
��ӂ���A���q���ꂽ�����H�אs�������q���̗ʂ́A
�Q�E�w�{�Q�E���w�E�P�U���X�E�x�E�P�U���(1)
�R�E�w�{�R�E���w�E�P�O���P�W�E�x�E�P�O���(2)
�T�E�w�{�T�E���w�E�y���R�T�E�x�E�y���(3)
(1)����(2)������w����������ƁA���w���Q�x���(4)
�܂�(1)����(3)������w�����������
(�P�U�O�|�P�O�y)���w��(�V�Q�O�|�V�O�y)�x���(5)
�����Ł��w���Q�x�ł��邩��
(5)���́A(�P�U�O�|�P�O�y)�Q�x��(�V�Q�O�|�V�O�y)�x�@�ƂȂ�B
����������Ɓ@�y���W
�]���āA�Tac�̓y�n�ɂR�T�����q����ƂW���ԂŐH�אs�������ƂɂȂ�B
�l�@
���Ƃł͂Ȃ��̂ŁA�����̂��b�ł��B
�k�C���ł́A�`���V�[�������A���n�ʂ͂V(t/ha/45d)�ʁB�i�����������������j
���Z����Ɩ�U�R(kg/ac/d)�ƂȂ�B���Ȃ킿���w���U�R
(4)������A�P��������̖q������ʂ͂R�P�D�T(kg/h/d)
�����ł��ƁA���ʂ𑽂����邽�ߖq���͂W(kg/h/d)�ɉ������A
���͔Z�����������a����悤�ł��B
�]���āA���q����Ă��鋍�̓z���X�^�C���ł͂Ȃ��悤�ł��ˁI
�ܘ_�A�C�ۏ������ŁA�������������Ƃ͎v���܂���̂łǂȂ����A���_�܂��͒{�Y�W�̕���
�����܂�����A���z���I
�h���_�����k�C���h�Ȃ�ł͂̍l�@�H�ł����B

�i�y���l�|���F��ӂ����̂炢�������� �j
�@�����́A�W���ł��B
�@���q�O�̖q���̗ʂƐL�т�q���̗ʂ̘a���A�����H�ׂ�q���̗ʂƓ������l���܂��B
���q�O�̒P�ʖʐϓ�����̖q���̗ʂ����A�P���ɐL�т�P�ʖʐϓ�����̖q���̗ʂ����A
�P��������ɋ����H�ׂ�q���̗ʂ����A���̓��������Ƃ���ƁA���̎����ł��܂��B
�@�@�Q�~���{�Q�~�P�U�~�����@�X�~�P�U�~���@�E�E�E�E�E�E(1)
�@�@�R�~���{�R�~�P�O�~�����P�W�~�P�O�~���@�E�E�E�E�E�E(2)
�@�@�T�~���{�T�~�@���~�����R�T�~�@���~���@�E�E�E�E�E�E(3)�D
(3)��肄�����^(�V���|��)�@�ƂȂ�̂ŁA(1)�E(2)��A�������Ă��Ƃ��ɂ��ĉ�����
�@�@�������^�Q�O�A�������^�S�O
��������Ƃ����W(��)�ƂȂ�܂��B
���m�����S����������ł��������o�܂��B
����͒萔�����Ȃ����ƂƁA�����P�̎��ɂ����Ȃ����߂ł��B�t�ɂ��A���A���͌���ł��܂���B
(1)�E(2)���炁�Ƃ��ɂ��Ă��ŕ\���Ă݂�ƁA�����S�O���A�����Q���ƂȂ�܂��B
����́A���{�����S�Q���Ȃ̂ŁA�P���Ȃ�P�G�[�J�[�łS�Q���̋��������邱�Ƃ��Ӗ����܂��B
�܂��A�P�G�[�J�[�łQ���܂łȂ�q��������Ȃ����Ƃ��Ӗ����܂��B
�@���āA��̕�����������ƁA
�@�@���{�P�U�����V�Q���@�E�E�E�E�E�E(1)�f
�@�@���{�P�O�����U�O���@�E�E�E�E�E�E(2)�f
�@�@���{�@�������V�����@�E�E�E�E�E�E(3)�f�D
�����ŁA(2)�f�|(1)�f�����āA�����Q���ƂȂ�܂��B
(3)�f�̂��Ƃ��̌W���̔�́A�P�F�V�ł��B(2)�f�̂��Ƃ��̌W���̔䂪�A�P�F�U�Ȃ̂�
�i(1)�f�̏ꍇ�͂Q�F�X�j�A
�Q�����S����(2)�f��������ƁA
�@�@���{�W�����T�U���ƂȂ�A���Ƃ��̌W���̔���P�F�V�ɂł��܂��B������T�{�����
�@�@�T���{�S�O�����Q�W�O��
�@�@�T�~���{�T�~�W�~�����R�T�~�W�~���D
�����(3)�Ɣ�r���ĂW���ƍl���邱�Ƃ��ł��܂��B

�i�y���l�|���F�`�{�@�_�j
���P���̋����P���ɐH�ׂ�q���̗ʂ��@�P���E���@�ƕ\�����܂��B
�Q�G�[�J�[�ɂX���̋��@���@�P�G�[�J�[������S�D�T��
�R�G�[�J�[�ɂP�W���̋��@���@�P�G�[�J�[������U��
�T�G�[�J�[�ɂR�T���̋��@���@�P�G�[�J�[������V��
�܂��A���̂悤�ɂP�G�[�J�[������Ɋ��Z���čl�����
�ʐς̍��ɂ��e�����l������K�v���Ȃ��Ȃ�܂��B
�i���Ƃ��Ɛ����Ă����q���̗ʂ������ŁA�P���ɋ��̐������ōl����悢�A�Ɓj
���F�S�D�T���̂����̂O�D�T���̋��́A�Y�܂���ݑ܂��Q�����Ȃ����H�ł���A
�P���ɐH�ׂ�q���̗ʂ͑��̋��̔����Ƃ��܂��i�j
�S�D�T���̋����P�U���ԂɐH�ׂ�q���̗ʂ�
�@���@�S�D�T�~�P�U���V�Q���E��
�U���̋����P�O���ԂɐH�ׂ�q���̗ʂ�
�@���@�U�~�P�O���U�O���E��
���Ƃ��Ɛ����Ă����q���̗ʂ͓����������͂��Ȃ̂�
���̍��́@�V�Q�|�U�O���P�Q���E���@����
�P�O���`�P�U���̂U���ԂɐL�т��q���̗ʂƂ������ɂȂ�܂��B
�܂�A�P���ɐL�т�q���̗ʂ́@�P�Q���U�@��
�P�G�[�J�[������@�Q���E���@�ł��鎖��������܂��B
������
�P�U���ԂŐL�т�q���̗ʁ@���@�Q�~�P�U���R�Q���E��
�P�O���ԂŐL�т�q���̗ʁ@���@�Q�~�P�O���Q�O���E��
�V�Q�|�R�Q���U�O�|�Q�O���S�O���E���@�̖q����
�ŏ��ɐ����Ă����Ƃ������ɂȂ�܂��B
���āA�V���̏ꍇ�ɂȂ�܂���
�P���ɐH�ׂ�q���̗ʂ͓��R�@�V���E���A
�����ĂP���ɐL�т�q���̗ʂ��@�Q���E���@�Ȃ̂�
�����P���Ɂ@�T���E���@�����q���͌����Ă����Ƃ݂Ȃ������ł�
�ŏ��ɐ����Ă���q���́@�S�O���E���@�Ȃ̂�
�S���Ȃ��Ȃ�܂Ł@�S�O���T���W���ԁ@�ł��鎖��������܂��B
���_�Ƃ��āA�P�G�[�J�[�̓y�n�ɂV���̋�����Ƃ���
�T�G�[�J�[�̓y�n�ɂR�T���̋�����Ƃ���
�W���ԂŖq���͐H���s������Ă��܂����ƂȂ��ł��B

�i�y���l�|���F�����@���L �j
2�G�[�J�[��...��3�{����ƁA6�G�[�J�[��27���ł�16��������܂�
3�G�[�J�[��...��2�{����ƁA6�G�[�J�[��36���ł�10��������܂�
������2�{�@3�{�ɂ͂Ȃ�܂���ˁB
�ŁA1����1���ɐH�ׂ�ʂ��P�Ƃ���ƁA�O�҂�24�~16=432
��҂�36�~10=360�ŁA����72���A6���ԂŁA�L�т��q���̗ʂɂȂ�܂��B
1���Ԃł�72/6�~10=120�L�тĂ��܂�����A���q�O��360-120=240����܂����B
1�G�[�J�[�ł́A240/6=40����A1����72/6����12�@12/6�G�[�J�[=2�L�т܂��B
����āA�T�G�[�J�[�ł́A�͂��߂�40�~5��200����A�����2�~5��10�L�т���̂�
1����35�Â���Ă����̂ŁA1����35-10=25����Ă����܂��B
�����ŁA200/25=8���ŐH�אs�������ɂȂ�܂��B
�A�����������g��Ȃ��ƁA�ω��̏�������̂ŁA���\�D���ɂȂ�܂����B

�i�y���l�|���F���N�g�j
����8��
�Q�G�[�J�[�A�X���̋��A�P�U��
�R�G�[�J�[�A�P�W���̋��A�P�O��
�T�G�[�J�[�A�R�T���̋��A�H�� �Ƃ����^����ꂽ������
�P�G�[�J�[�A4.5���̋��A�P�U��
�P�G�[�J�[�A�U���̋��A�P�O��
�P�G�[�J�[�A�V���̋��A�H�� �ƕς��܂��B
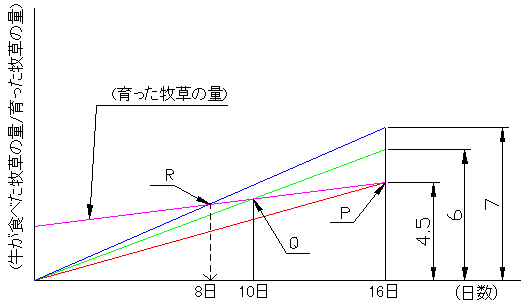
���ꂼ��̏ꍇ�́A�����H�ׂ����ʂ́A4.5:6:7�̊����ɂȂ�A
�O���t�ɂ���ƈȉ��̂悤�ɂȂ�܂��B
�܂��A������q���̗ʂ́A��ʂ͈��Ȃ̂ŁA�������A�_P�AQ��ʂ钼���ɂȂ�܂��B
�]���āA���߂铚���́A�_R�̓��� 8���ƂȂ�܂��B

�i�y���l�|���F�����̊�{�j
(�����)
�@�P�ʖʐςɂ��āC���q�O�̖q���̗ʂ����C1���ɐL�т�q���̗ʂ����Ƃ���.�܂��C1���̋���1���ɐH�ׂ�q���̗ʂ����Ƃ����ƁC
2(x+16y)��16�E9���E�E�E(1)
3(x+10y)��10�E18z�E�E�E(2)
���
5(x+ny)�����E35z�E�E�E(3)
�ƂȂ邎�����߂܂�.
(1)���Cx+16y=72z�E�E�E(4)x/z=��,y/z=t�Ƃ�����
(2)���x+10y=60z�E�E�E(5)
(3)���x+ny=7nz�E�E�E(6)
(7)(8)���s=40,t=2-----------------------------------------------------------------------------
������(9)�ɑ������,
40+2n=7n
�䂦��n=8(��)�E�E�E(�b��I�ȓ�)
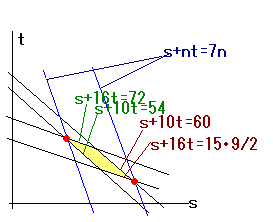
x/z=��,y/z=t�Ƃ�����(7)(8)�����̈���ł�(9)�������̒l�͈̔͂����߂邱�ƂƂȂ�܂�.
15�E9/2��s+16t��72�E�E�E(7)
54��s+10t��60�E�E�E(8)
(3)���s+nt=7���E�E�E(9)
������

| �����@���L | �`�{�@�_ | ���Îu |
| ��ӂ����̂炢�������� | judas | ���N�g |
| �˂� | �����̊�{ | �C�V�� |
| ���̗��� | temutin |

����̓j���[�g��(1642�`1727)���l�����p�Y���������ł��B
�j���[�g���̎���̋��ƁA�k�C���ň���ƥ���ƍl����Ɖ������������낢�ł��ˁB
����̖���������ɂ���ƁA���m���S�̂R�{�Ƃ������ƂɂȂ�܂��B
���̏�Ԃ��ƈ�ʓI�ɂ͉������߂邱�Ƃ��ł��܂���ł����A
NO.7�@��ӂ����̂炢���������̉ɂ���悤�ɁA
�萔�����Ȃ����ƂƁA�����P�̎��ɂ����Ȃ����߂ɁA������������Ƃ��ł��܂��B
���ĕ����������Ă邱�Ƃ̈Ӗ��́A���ꂪ�q�ϓI�Ɉ�����A�@�B�I�ɉ������Ƃ��ł���Ƃ������Ƃ��Ǝv���܂��B
�������Ȃ���A�����ċq�ϓI�ɂ����ɁA�����܂ł��q���ɂ�������čl����̂���������ł��ˁB
�i��������m��Ȃ����w���ɐ�������ɂ͂�������������Ȃ��I�@
�t�ɁA�������ɗ���Ȃ��ʼn����Ƃ����̂��厖��������܂���B�j
NO.10�@���N�g�����̉͑N�₩�I�@ �O���t���g�����f���炵���ł��ˁB
�����܂߂Ă݂Ȃ����ʼn������ŁANO.11�@�����̊�{�����͕s�����ʼn����Ă��������܂����B
���ۂɂ́A�q���̐����͘A���I�ɋN����ł��傤����A�����ɂ��������l����ׂ��Ȃ̂ł��傤�B

 E-mail
E-mail
 �߂�
�߂�
 top
top