1.折り紙を、もとの面積の5分の1の正方形になるように折ってください。
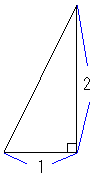
2.図のような直角三角形5枚で1つの正方形を作ってください。
ただし、そのうち1枚はハサミで1ヶ所だけ切ってもよいものとします。
Weekend Mathematics/問題/問題50
50.面積5分の1の問題
1.折り紙を、もとの面積の5分の1の正方形になるように折ってください。

2.図のような直角三角形5枚で1つの正方形を作ってください。 ただし、そのうち1枚はハサミで1ヶ所だけ切ってもよいものとします。
1.数学パズル/沖田浩/中経出版
2.秋山仁の中学生おもしろ数学/日本放送出版協会
(ペンネ−ム:ねこ)
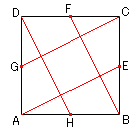
図のように、辺の中点と頂点を結んだ線で折り返す。
4回行えば中央の正方形は元の正方形の1/5の面積になる。
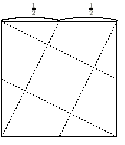

(ペンネ−ム:高橋 道広 )
解1
まず図のような折り紙を用意します。次にそれを小学生以上の年齢の人に
渡します。するとたいていの人は、折れるでしょう。もとの折り紙の形は何もいって
いませんから。(今はいろいろな形の折り紙が売られています)

解2
さて、折り紙を5×5の25等分に折ります。そして、図のように、折り目を選
んでうまく折ると、面積1/5の正方形の出来上がり。5×5の折り方については、ここに
は書くスペースがないので...というのはこの間使った言い訳なので、まず8×8に折っ
て、そのうち5×5の部分をはさみで切った折り紙を用意するということではどうでしょうか。
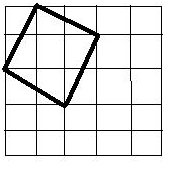
解3
いいかげんおこられそうなので、最後の解答を...
折り紙の頂点と、各辺の中点を結んで折ります。
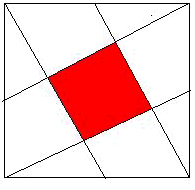
正方形の一辺の長さを1とします。
いたるところ1:2: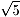 の直角三角形が
できますね。
の直角三角形が
できますね。
一番大きいのが 1/2 1 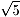 /2
/2
一番小さいのが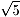 /5
/5 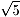 /10 1/2
/10 1/2
真中にある正方形の一辺は、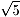 -
-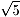 /5-
/5-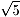 /10
=
/10
=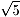 /5
/5
(一番大きな三角形の斜辺から、一番小さい三角形の2辺を引く)
面積は1/5ですね。
算数では、
一番小さい三角形と中くらいの三角形について、中点連結定理から中にある正方形の
長さを1とすると、中くらいの三角形の直角をはさむ二辺の長さが2と1であること
がわかります。大きな正方形は、小さい正方形と中くらいの直角三角形4つなので
1+4×(1/2)×2×1=5ですから、大きな正方形は小さい正方形の5倍の面積です。
この解答は図がヒントになりましたね。

(ペンネ−ム:中数の基本)
(1) 次の図において,赤で示した線分は縦の長さの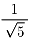 です.
です.
そこで右図において●で示した線分は,
正方形の一辺の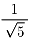 です.
です.
したがって,黄色rで示した正方形の面積は元の正方形の面積の1/5です.

(ペンネ−ム:judas)
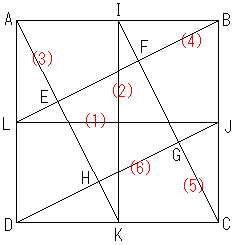
1. 1/5の正方形
正方形の一辺の長さを1とする。
また、EFGHは各辺の中点とする(IJKLはそれぞれの交点)。
すると、各頂点とEFGHを結んだ線はそれぞれ直交もしくは平行となる。
正方形の中にできる直角三角形はすべて大きい直角三角形(たとえばABF)と相似と
なり(反転したものではあるが)、斜辺以外の2辺の長さの比は1:2となる。
従って、AI:IJ:JFは2:2:1となるので、AFの長さは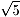 /2だから、
IJの長さは
/2だから、
IJの長さは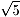 /5となる。
/5となる。
JK,KL,ILも同様に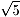 /5となり、
各辺は直交するのでIJKLは面積1/5の正方形となる。
/5となり、
各辺は直交するのでIJKLは面積1/5の正方形となる。

(ペンネ−ム:夜ふかしのつらいおじさん )
1.
1)折り紙を四つ折りにして各辺の中点(赤)を見つけ開く。
(このときの十字の折り目は使わない)
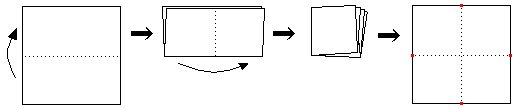
2)図のように角と辺の中点を結ぶ線(赤)で折ってから開く。
(A-E, B-F, C-G, D-H)
3)図のように、A-E, C-G の折り目で折る。
次に B-F, D-H の折り目で折るともとの正方形の5分の1の大きさの正方形ができる。
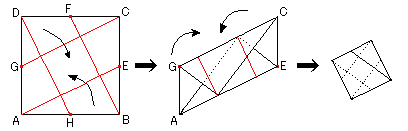

(ペンネ−ム:temutin)
折り紙を(1)〜(6)の順に折る。
出来上がった四角形EFGHが求める正方形である。
△JDCと△CDGが相似であること、DH=GH、四角形のそれぞれの角が90゚であること等の証明は省略し、
正方形の面積が折り紙の1/5となっていることの検証のみ記述する。
折り紙の辺の長さをaとおく。
ピタゴラスの定理から
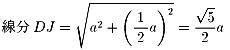
△JDC∽△CDGであるから、GH=x とすると
2x:a=a: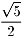 a
a
ゆえに、x=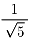 a
a
従って、正方形の面積は (1/5)a2
これは、折り紙の面積の1/5である。

(ペンネ−ム:海坊主)
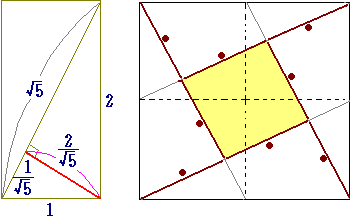
三角形は底辺が1、高さが2の直角三角形でしたよね。直角を除いた2角をA、Bとします。
直角三角形の1でも2でもない辺を、作るべき正方形の辺とします。
角Aと角Bが隣り合うようにして直角三角形を4つ並べて行くと真中に辺の長さ1の正方
形の分が空いた正方形が出来ます。
あとは、この辺の長さ1の部分を埋めるわけですが、この部分は残り1つの直角三角形を
高さ2の辺を底辺の部分から
長さ1の部分に目盛りを取りその目盛りから底辺と平行に切って、台形の部分と直角三角
形の部分を先に上げた1でも2でもない辺であわせると、辺の長さ1の正方形が出来る。
それを空いている部分に埋めると、見事直角三角形5つで正方形が出来るわけである。

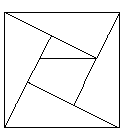
(ペンネ−ム:ねこ)
図のように並べる。 中央の正方形を作るのにはさみを1回使用。

(ペンネ−ム:細井 夏樹)
1つの三角形を高さ1cmの所で切り、下図のように並べる。
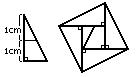

(ペンネ−ム:夜ふかしのつらいおじさん )
2.図のようにつなげる。
1つの直角三角形は下図右のように高さ1のところで水平に切り回転しても
と斜辺のところであわせて正方形にしておく。
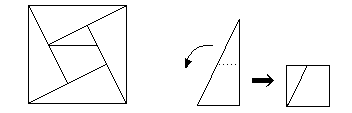
【説明】
もし1番の折り紙の1辺の長さが5の平方根ならば、2番の正方形は折り紙と同じ大きさです。
2番の直角三角形の面積は1なのでできあがる正方形の面積は5です。
だから正方形の1辺の長さは5の平方根です。
直角三角形の斜辺の長さは5の平方根ですからそれが正方形の1辺になるように大小の内角が
角にくるようにします。中央には1辺1の正方形がすっぽり入ります。
1番で例えば、三角形ABEの直角をはさむ二辺の比はたて:横が1:2です。
これは2番の直角三角形と相似なのです。

(ペンネ−ム:judas)
2. 5枚で正方形
三角形の面積は1なのでもとめる正方形の面積は5、その一辺の長さは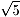 となる。
となる。
5枚中一枚しか切り貼りしてはいけないので、残りの4枚の斜辺(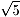 )がそのまま求
める正方形の辺となる。
)がそのまま求
める正方形の辺となる。
直角三角形の直角以外の2角の和は90度なので、ひとつの直角三角形の直角でない角
に次の三角形のもう一方の直角でない角をつけるようにすれば、ちょうど正方形の枠
ができる。
すると内部に一辺が1の正方形の穴ができる。
残った直角三角形の斜辺と長いほうの辺の中点を結んだ線できると、その2つの組み
合わせでちょうど一辺が1の正方形ができるので、それを入れると5倍の正方形ができ
る。
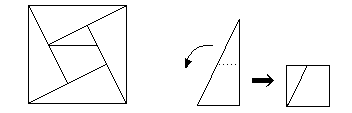

(ペンネ−ム:高橋 道広 )
解1
図のように4枚の直角三角形4枚を並べる。のこりの1枚は、はさみで真っ
二つにしてごみ箱へすてる。というのでどうでしょうか。
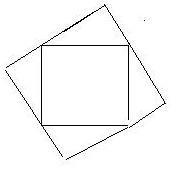
しかし、この解答では、2つの正方形を作ってしまいました。
では、下の図のように、直角三角形1つをひっくり返しておくと良いでしょう。
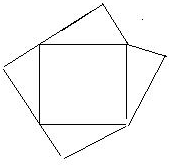
解2
これは、たぶん三平方の定理の証明が自分の頭の中にあって、それで、ひらめいた
と思います。
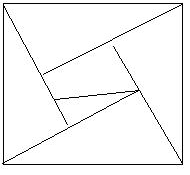
1がヒントになったようにも思います。
この解答は面白くないので、説明しません。

(ペンネ−ム:中数の基本)
(2) 一辺が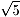 の正方形を作るとよいから,右図で赤で示した線で切り,
白い部分に移動します.
の正方形を作るとよいから,右図で赤で示した線で切り,
白い部分に移動します.
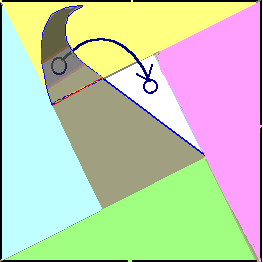

(ペンネ−ム:temutin)
図のように並べる。
1枚はBCでカットし、カットしてできた△ABCを△A'B'Cにおく。
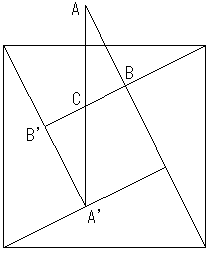

| ねこ | 中数の基本 | 高橋 道広 |
| 海坊主 | 夜ふかしのつらいおじさん | judas |
| 細井 夏樹 | temutin |

相変わらず、高橋 道広さんの解答はユニークで笑えます!!
今回、似たような問題をあえてこの順番で出題しました。
最初に1番の問題を読んで、1/5なんて半端な(どこがどう半端なのかわかりませんね、かなり主観的)
正方形が本当に作れるのでしょうか? と思った方も多いのではないかと思います。
私もそう思いました。
とりあえず1番は置いておいて、2番を解いてみる。
この直角三角形はちょうど斜辺が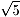 なので、これを1辺として作っていけばいい。
なので、これを1辺として作っていけばいい。
ここまでくると、これが1番のヒントとなり、5という数字が半端でなく、
むしろ必然的な数字に思えてくるから不思議!
(この感覚が私は好きです。)
ただし、要注意!
1番の解答は2番と同じ、というのはだめです。
1番と2番では、仮定と結論がまるで逆です。
1番は、任意の正方形がまずあり、それをどうやって分割していくかということが問題で、
そのやり方を説明していただかないといけないと思います。
図をかくと同じものになるかもしれませんが、まず正方形ありきという点が違うわけです。
また、厳密にいうと、分割の仕方と共にそれが確かに1/5になっているという証明も必要かと思います。

 E-mail
E-mail
 戻る
戻る
 top
top