Weekend Mathematics/問題/問題46
46.数学オリンピックの問題
シドニーオリンピックは私達に多くの感動を与えてくれ、今日閉会式を迎えました。
そこで、今回は数学オリンピックの問題からです。
n2を120で割ると1余るような、120以下の正整数nはいくつあるか。
第3回 日本数学オリンピック予選
数学オリンピック 1991〜1996
(財)数学オリンピック財団編
日本評論社
答えと解説
(ペンネ−ム:佐々木一樹)
答え 16個
やり方

(ペンネ−ム:かつ)
今回のは、なかなかこれといったことがわからなかったので計算してとりあえず求めてみました。
かといって120個の整数をすべて確かめるのも大変なのでまずは確認する数を減らす作業から入りました。
今回の問題は
n2を120で割ると1余ると言うことから、
n2=120k+1(kは任意の正整数(0を含む))
と言うように出来ます。
つまりn2は下一桁が1になると言うことが分かります。
そこでnになりうる120以下の正整数のうち、平方して下一桁が1になるのは、
1の位が1または9のときのみと言うことになります。
あとはひたすら計算してみました。
そうすると
| 12=120・0+1 |
| 112=120・1+1 |
| 192=120・3+1 |
| 292=120・7+1 |
| 312=120・8+1 |
| 412=120・14+1 |
| 492=120・20+1 |
| 592=120・29+1 |
| 612=120・31+1 |
| 712=120・42+1 |
| 792=120・52+1 |
| 892=120・66+1 |
| 912=120・69+1 |
| 1012=120・85+1 |
| 1092=120・99+1 |
| 1192=120・118+1 |

(ペンネ−ム:246)
答え: 16個
方法:
120で割って1が余るとなると、下1桁は必ず1となるということで、
2乗して下1桁が1になる値は、下1桁が 1,9となる。
この時点で 24個に絞られる。
次に120の公約数(2,3,4,5,6,8,10,12,15,20,24,30,40,60)で割れない数を取り出す。
ここで振り分けられる数が、9,21,39,51,69,81,99,111 の8個。
これをのぞいた数
1,11,19,29,31,41,49,59,61,71,79,89,91,101,109,119
の16個が該当する・・・

(ペンネ−ム:マサボー )
n2 = 120A+ 1とおける。
2乗して1の位が1になるものの1の位は1と9であるから、
n = 10B + 1あるいは10B + 9となる(0≦B≦11)
| n2 | = (10B + 1)2 |
| = 100B2 + 20B + 1 | |
| = 20B(5B+1) + 1 |
| n2 | = (10B + 9)2 |
| = 100B2+180B+81 | |
| = 100B2+180B+80 + 1 | |
| = 20(5B2+9B+4) + 1 | |
| = 20(5B+4)(B+1) + 1 |

(ペンネ−ム:hirai)
問を数式表現すると
n2=120A+1(但し A≧0の整数) (n≦120)・・・(1)
A≧0の整数なので、n2の一の位は常に1である。
整数の2乗数で、一の位が1になる数は0〜9の2乗を調べて、
(10x+1)2または、(10y+9)2で表せる。・・・(2)
ここで、x、yは、0≦x、y<12を満たす整数である。
(1)(2)より、
| x | 左辺 | 6を因数に含むもの判定 |
|---|---|---|
| 1 | 1× 6 | ○ |
| 2 | 2×11 | × |
| 3 | 3×16 | ○ |
| 4 | 4×21 | ○ |
| 5 | 5×26 | × |
| 6 | 6×31 | ○ |
| 7 | 7×36 | ○ |
| 8 | 8×41 | × |
| 9 | 9×46 | ○ |
| 10 | 10×51 | ○ |
| 11 | 11×56 | × |
| x | 左辺 | 6を因数に含むもの判定 |
|---|---|---|
| 0 | 1× 4 | × |
| 1 | 2× 9 | ○ |
| 2 | 3×14 | ○ |
| 3 | 4×19 | × |
| 4 | 5×24 | ○ |
| 5 | 6×29 | ○ |
| 6 | 7×34 | × |
| 7 | 8×96 | ○ |
| 8 | 9×44 | ○ |
| 9 | 10×49 | × |
| 10 | 11×54 | ○ |
| 11 | 12×59 | ○ |
1.2.より 1+7+8=16
従って、問の条件を満たす正整数は16個

(ペンネ−ム:少年H)
n2=120×p+1
n2−1=120×p
(n−1)(n+1)=23×3×5×p
pはp≧0の整数とする。
n=1は解である。
右辺は偶数であるから左辺も偶数。すなわちnは奇数である。
また一方、右辺は5の因数が含まれるから、左辺も5の因数が含まれる。
よって、nの候補は、
| n= | 9, | 11 |
| 19, | 21 | |
| 29, | 31 | |
| 39, | 41 | |
| 49, | 51 | |
| 59、 | 61 | |
| 69, | 71 | |
| 79, | 81 | |
| 89, | 91 | |
| 99, | 101 | |
| 109, | 111 | |
| 119 |
| n= | 9×, | 11 |
| 19, | 21× | |
| 29, | 31 | |
| 39×, | 41 | |
| 49, | 51× | |
| 59、 | 61 | |
| 69×, | 71 | |
| 79, | 81× | |
| 89, | 91 | |
| 99×, | 101 | |
| 109, | 111× | |
| 119 |

(ペンネ−ム:高橋 道広)
答え 16個
文字はすべて自然数とします
n22=120x+1とおくと n22-1=120xより(n+1)(n-1)=120x
n+1またはn-1が偶数より、n=2k-1とおけます。
(2k-1-1)(2k-1+1)=120x より k(k-1)=30x
k(k-1)は必ず2の倍数なので、k(k-1)が15の倍数であれば良いから
まず、5の倍数であることに着目して
k=15m,15m-4,15m-5,15m-9,15m-10,15m-14
このうちkまたはk−1が3の倍数であるものは
k=15m,15m-5,15m-9,15m-14
これをn=2k-1に代入して
n=30m-1,30m-11,30m-19,30m-29(m=1,2,3…)
つまり30の倍数までに4つずつあることになる。
120までは4×(120/30)=16個となります。

(ペンネ−ム:ウェルテル)
n=m+1とおく n・n=(m+1)・(m+1)
nの2乗を120で割ったときに余りが1になるにはmの2乗+2mが
120の倍数でなくてはならない。
m・m+2・m=m・(m+2)
このときmまたはm+2を2・3・5の倍数とするとm・(m+2)は120の倍数になる。
(なぜならば2つの連続する偶数のどちらか1つは2・2の倍数であるから)
(120=2・2・2・3・5)
よってm=30、60、90 m+2=30、60、90、120
m=28、30、58、60、88、90、118
また m が6の倍数であるときm+2が5の倍数である場合にもm・(m+2)=120が成り立つ。
m+2は偶数だから10の倍数であればよい。
そんなmをみたす数は0以上119以下の範囲では18、48、78、108(18+30・n)
m が10の倍数のときm+2が3の倍数である場合にもm・(m+2)=120が成り立つ。
同様にm+2は6の倍数であればよい。
そんな m をみたす数は0以上119以下の範囲に10、40、70、100(12+30・n)
(このときm+2は1の位が2の数)
n=1のときもあまりは1になる
n=1、11、19、29、31、41、49、59、61、
71、79、89、91、101、109、119

(ペンネ−ム:kiyo)
120で割り1余る数は、
1+120×(m−1)=120m−119 mは正整数。
であるから、Nの1位の数は1または9でなければならない。 (1)
1≦N≦120。(2)
120=23×3×5
したがって、2,3,5の素因数を持たないものでなければならない。(3)
(1)、(2)、(3)を満たすものは、
| 1 | ○ | 1 |
| 9=32 | × | |
| 11 素数 | ○ | 2 |
| 19 素数 | ○ | 3 |
| 21=3×7 | × | |
| 29 素数 | ○ | 4 |
| 31 素数 | ○ | 5 |
| 39=3×13 | × | |
| 41 素数 | ○ | 6 |
| 49=72 | ○ | 7 |
| 51=3×17 | × | |
| 59 素数 | ○ | 8 |
| 61 素数 | ○ | 9 |
| 69=3×13 | × | |
| 71 素数 | ○ | 10 |
| 79 素数 | ○ | 11 |
| 81=34 | × | |
| 89 素数 | ○ | 12 |
| 91=7×13 | ○ | 13 |
| 99=3×11 | × | |
| 101 素数 | ○ | 14 |
| 109 素数 | ○ | 15 |
| 111=3×37 | × | |
| 119=7×17 | ○ | 16 |

(ペンネ−ム:ねこ )
条件より、n2の1の位は1となるのは明らか。
よってnの1の位は1か9となる。
n=10N±1型のnについて調べればよい。(以下複号同順)
n2=120k+1と書いたとき、
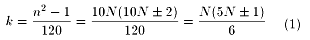
が整数となればよい。
そこで、N=6m±l(l=0,1,・・・5)について
N(5N±1)を6で割った余りを調べてみる。
| N(5N±1) | =(6m±l){30m±(5l+1)} |
| =180m2±(60l+6)m+l(5l+1) | |
| =l(5l+1) (mod 6) (2) |
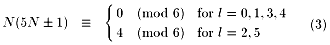
よって、N(5N±1)が6で割り切れるのは
N=6m±l(l=0,1,3,4)のとき。
書きなおして、N=3m'±l'(l'=0,1)のときとなる。
これをn=10N±1に代入して、条件を満たすnの式が得られる。
| n=10N±1 | =10(3m'±l')±1 |
| =30m'±(10l'+1) (l'=0,1) (4) |

(ペンネ−ム:夜ふかしのつらいおじさん )
答えは16個です。(n=1,11,19,29, 31,41,49,59, 61,71,79,89, 91,101,109,119)
nの2乗を120で割ると1余るのですから商をpとすると、
n2=120×p+1
n22-1=120×p
∴(n-1)(n+1)=2×2×2×3×5×p
上式の右辺は偶数なのでnは奇数です。nを奇数とすると(n-1)と(n+1)とは隣り合う
偶数なので、その積(n-1)(n+1)は、必ず2×2×2の倍数です。
あとは、3と5の倍数になるように考えればよいわけです。
下の表は(n-1)か(n+1)のどちらかが3や5の倍数かどうかを調べたものです。
0はすべての数の倍数としています。
表のように3の倍数は3個ごとの周期で、5の倍数は5個ごとの周期で繰り返します。
ですから15(=3×5)の倍数は15個ごとの周期で繰り返します。
| n | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n-1 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 |
| n+1 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
| 3 | o | x | o | o | x | o | o | x | o | o | x | o | o | x | o |
| 5 | o | x | x | x | o | o | x | x | x | o | o | x | x | x | o |
| 15 | o | x | x | x | x | o | x | x | x | o | x | x | x | x | o |

(ペンネ−ム:水の流れ)
120=23×3×5 から、
「120で割った余りが1である」を、「8で割っても1余り、3で割っても1余
り、5で割っても1余る」
と言いかえることができる。
ここで、n2を(1≦n≦120)を考える。
(1)「n2を8で割ると1余る」ということは、nを8で割った余りが1,3,
5,7である。即ち、nが奇数であることと同じである。」
(2)「n2を3で割ると1余る」ということは、nを3で割った余りが1か2で
ある。」
(3)「n2を5で割ると1余る」ということは、nを5で割った余りが1か4で
ある。」
以上(1)〜(3)より、「n2を120で割ると1余る」は、
「nは奇数で、3で割ると1か2余り、5で割ると1か4余る」と言いかえことがで
きる。
このような数は、2×3×5=30を1周期とするので、1〜30までについて、
具体的に調べると、適しているのが、1、11,19,29 の4つの数だけであ
る。
したがって、120÷30=4から、4周期分を考えて4×4=16(個)・・・(答え)
次に、こんな便利な定理がありますので、紹介します。
【中国剰余定理】
k、m、nをどの2数も互いに素な自然数とするとき、
kで割るとp(0≦k≦k−1)余り、
mで割るとq(0≦q≦m−1)余り、
nで割るとr(0≦r≦n−1)余るような自然数は、
1〜kmnのkmn個の中にちょうど1つ存在する
『証明』
kで割るとp余り、mで割るとq余り、nで割るとr余る自然数が1〜kmn個の中に
2個あったとし、その2つをM、Nとする。
すると、M−Nはkでもmでもnでも割り切れるから、k、m、nのどの2数も互
いに素であることより、kmnで割り切れることになるが、
M、Nはどちらもkmn以下の自然数だからM−Nはkmnより小であることに矛盾する。
よって、題意を満たす自然数は、1〜kmnに多くても1個しかない。
一方、k、m、nで割ったときの余りはそれぞれk、m、n通りなので、
余りの組み合わせはkmnしかない。
よって、題意を満たす自然数が1〜kmnに1つもないとすれば、これも矛盾する。
以上より、題意を満たす自然数は1〜kmnにちょうど1個存在する。
ここで、今月の問題に適用すると、
8で割った余りが1,3,5,7の4通り、
3で割った余りが1か2の2通り、
5で割った余りが1か4の2通りだから、
「8で割っても1余り、3で割っても1余り、5で割っても1余る」
を満たす自然数は、8、3,5のどの2数の互いに素より、
1〜120までに題意を満たす自然数は4×2×2=16(通り)・・・(答)

(ペンネ−ム:浜田 明巳)
答は16個.
今回もエクセルのマクロで作りました.
簡単に表型式で表示出来るのでこのソフトが一番プログラムを組みやすいものです.
|
Sub Macro1()
Dim 答 As Integer
Dim n As Integer
Cells(1, 1).Value = "答"
Cells(1, 2).Value = "n"
Cells(1, 3).Value = "n^2"
Cells(1, 4).Value = "商"
答 = 0
For n = 1 To 120
If (n * n) Mod 120 = 1 Then
答 = 答 + 1
Cells(答 + 1, 1).Value = 答
Cells(答 + 1, 2).Value = n
Cells(答 + 1, 3).Value = n * n
Cells(答 + 1, 4).Value = (n * n) \ 120
End If
Next
End Sub
|

(ペンネ−ム:中数の基本)
ご本人の了解を得て、ソースも掲載します。
<form name="asao"><input type="button" value="ここを押す" onClick="aaa()">
<textarea name="ta1" rows="2" cols="62" wrap="virtual"></textarea>
</form>
<script language="javascript">
gaitounosuu = '';
count = 0;
function aaa()
{for(kk = 1; kk <= 120; kk++)
{if(kk * kk % 120 == 1)
{gaitounosuu += kk + ',';
count++;
}
}
document.asao.ta1.value = gaitounosuu + 'の' + count +'個です.単純計算でごめんね.(Where have Math gone ?)';
}

| kiyo | 夜ふかしのつらいおじさん | 浜田 明巳 |
| 少年H | 高橋 道広 | 中数の基本 |
| 246 | ねこ | 水の流れ |
| 佐々木一樹 | hirai | かつ |
| マサボー | ウェルテル |

この問題を解くときに、n=1〜120まで2乗して120で割って余りを出してみるというやり
方があると思います。
プログラムを組むことで解答を出してくださった浜田 明巳さんや
中数の基本さんはこの方式です。
一方、佐々木一樹さんの解き方は、逆に120倍数+1で開法(平方根を求める)してみて
整数になるか調べるということです。
人によってアプローチの仕方が違うけれど、真実は1つというのが数学のおもしろさ
でもあると思います。
人間が計算するときには、なぜこんな遠回りなことをするのだろうと思っても、
コンピューターに相性のいいアルゴリズムというのもあると思います。
少年Hさんの解答では、6行目に左辺は偶数とありますが、
単に偶数というだけではなく、23=8の倍数であることを一言指摘した方がい
いと思います。(証明するほどのことはないのですけれどね。)
今回はここで【中国剰余定理】を紹介しようかと思っていたのですが、
水の流れさんが説明してくださっていますので、そちらをお読みください。
さて今回初めて、JavaScriptで書かれた解答をいただきました。
中数の基本の了解を得て、ソース表示も表に出させていただきました。
JavaScriptというスクリプト言語はホームページをかく、いわゆるタグの中に表現し、
それをブラウザ側で解釈し、実行します。
裏返せば、JavaScriptに対応していないブラウザをお使いの方は、うまく動作しないかもしれません。
(確認できていません、すいません。)
ホームページの表現力をupする意味でも興味がありますので、私も勉強してみようと思います。

 E-mail
E-mail
 戻る
戻る
 top
top