Weekend Mathematics／問題／問題42

４２．おはじきの問題

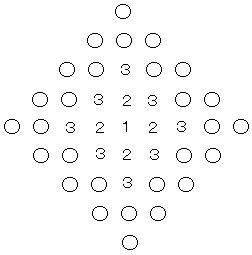
１．図のように数１をおき、次にこれを囲んで正方形状に数２を４個おく。 次にこの２を囲んで正方形状に数３を８個おく。 こうして最後に数ｎを正方形状に囲んでおいたとき、 これらの数のすべての和をｎの式で表せ。

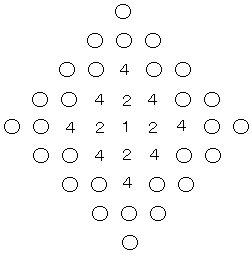
２．図のように数１をおき、次にこれを囲んで正方形状に数２を４個おく。 次にこの２を囲んで正方形状に数４を８個おく。 更にこの４を囲んで正方形状に数８を１２個おく。 こうして最後に数ｎを正方形状に囲んでおいたとき、 これらの数のすべての和をｎの式で表せ。

問題１

解答・その１

（ペンネ−ム：かつ）

数列の問題ですね。
一番外側にできる数の和を○項目とします。
そうするとすべての項の和が答えなので まず、第ｎ項目がわかればよいのでｎ項目を調べます。

１項 １
２項 ２×４（２−１）
３項 ３×４（３−１）
となり１項目以外から
ｎ項　ｎ×４（ｎ−１） と予想されます。
実際予想ではなく数ｎが一辺ｎ個並んでるから四辺でｎ×４（ｎ−１）になります。
これから和なので求める数は

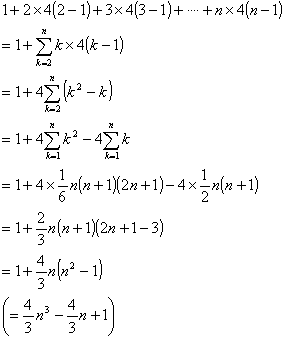
となります。

解答・その２

（ペンネ−ム：マサボー）

n 列目の個数は 4(n-1) ( n ≧ 2 , n=1 のとき1)。
よって n 列目の合計は 4n(n-1)( n ≧ 2 , n=1 のとき1)
求める合計 S_n は

問題２

解答・その３

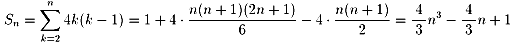
（ペンネ−ム：少年Ｈ）

内側からｎ番目の数字は、2^n-1
内側からｎ番目の数字の個数は、4(n‐1)（ただしｎ≧2）

内側からｎ番目	１	２	３	４	．．．．．．	ｎ
数字	20	21	22	23	．．．．．．	2n−1
個数	１	４	８	１２	．．．．．．	4(n−1)
それぞれの数字の合計	20×1	21×4	22×8	23×12	．．．．．．	2n-1×4(n-1)

よって総和は

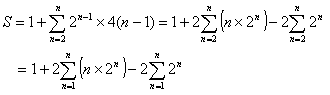
ここで、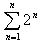は、 初項２、公比２の等比数列であるから、その和は２×(２^ｎ−１)である。

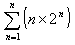	=	1×21+2×22+3×23+4×24+5×25+･･･+n×2n
	=	21+22+23+24+25+･･･+2n
		(21)+22+23+24+25+･･･+2n
		(21+22)+23+24+25+･･･+2n
		(21+22+23)+24+25+･･･+2n
		(21+22+23+24)+25+･･･+2n
		〃
		(21+22+23+24+25+･･･+2n-1)+2n

と変形すると、それぞれの行は、２×(２^ｎ−１)であり、ｎ行あるから、 総和は２ｎ×(２^ｎ−１)＝ｎ×２^ｎ＋１−２ｎ
また、かっこ内は、一般項が等比数列の和　２×(２^ｎ−１)となるから、
かっこ内の総和は、

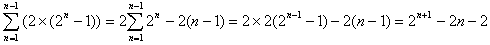
よってｎ行の総和からかっこ内の総和をひくと

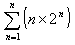＝ｎ×２^ｎ＋１−２ｎ−(２^ｎ＋１−２ｎ−２) ＝(ｎ−１)×２^ｎ＋１＋２

解答・その４

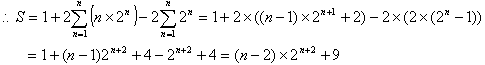
（ペンネ−ム：kiyo）

２×４，４×８，８×１２，１６×１６，３２×２０，６４×２４， １２８×２８，２５６×３２，・・・
８で割る。
０，１，４，１２，３２，８０，１９２，４４８，１０２４，・・・

A(0)=0 とする。
A(m)=m×2^m-1.............................................(1)
A(m)=2×A(m-1)+2^m-1............................(2)
(1),(2)より

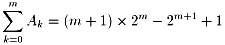
したがって求める和は

	8×{(m+1)×2m-2m+1+1}+1
=	(m+1)×2m+3-2m+4+9
=	(m+1)×8×2m-16×2m+9
	n=2m m:負でない整数とする。
=	(m+1)×8×n-16×n+9
	m=log2n であるから、
=	(log2n+1)×8×n-16×n+9
=	8×n×(log2n-1)+9

答え 8×n×(log₂n-1)+9

解答・その５

（ペンネ−ム：浜田　明巳）

同じ数字ずつに整理すると，

1    2 2   4 4 4    8 8 8 8    ...
     2 2   4   4    8     8
           4 4 4    8     8
                    8 8 8 8 

解答・その６

（ペンネ−ム：ねこ）

Let n = 2^m

S-1	= 2×4	+ 4×8	+ 8×12	+ ...	+ n×4×m
2(S-1)	=	4×4	+ 8×8	+ ...	+ n×4×(m-1)	+ 2×n×4×m

(S-1) - 2(S-1) (= 1 - S)	= 2×4 + 4×4 + 8×4 + ... + n×4 - 8×n×m
	= 4(2n-2) - 8×n×m
	= - 8 - 8×n(m-1)
S	= 1 + 8 + 8n(m-1)
	= 9 + 8n{log2n-1} //

解答・その７

（ペンネ−ム：夜ふかしのつらいおじさん）

内側からの順番	1,	2,	3,	・・・・	k,	・・・・	m
内側から並ぶ数	1,	2,	4,	・・・・	2k-1,	・・・・	2m-1 　←（注）
その数字の個数	1,	2,	8,	・・・・	4(k-1),	・・・・	4(m-1)

求める数 1・1 + 2・4 + 4・8 +・・・・+ 2^k-1・4(k-1) +・・・・+ 2^m-1・4(m-1)

初項 ａ₁＝１、　ａ_k＝２^k+1・（ｋ−１）　(ｋ≧２)の数列の和 Ｓ_mを求めればよい。

Ｓ_m を書き並べて Ｓ_m−２Ｓ_m より等比数列の和の公式を用いてまとめると、

　　Ｓ_m＝２^m+2・（m−２）＋９・・・・ ☆

（注）
さて、問題では最後の数が n とあるので、 2^m-1＝n とおくと、(m-1)＝log₂n だから

☆	＝２3・２m-1・（m−１−１）＋９
	＝８n・（log2n−１)＋９　（と答えるべきなのかな？）

「今回の問題は、答えにくいです。」とおしかりを受けました。 確かにシグマは表記しにくいですから、不適切だったと反省しています。

また問題２は、問題文に「最後の数がn」と書いてしまったので必要以上に面 倒な式になってしまいました。
Ｓ＝２^ｎ＋２・（ｎ−２）＋９　で正解でいいと思います。
式中のｎをすべてｍで置き換えた後に、n＝２^ｍー１という変換をすればいいわけですから・・・。

ある数ａ(これを初項と呼びます)に一定の数ｒ(公比)を次々とかけてできる数列を等比数列と呼びます。
等比数列の初項から第ｎ項までの和をＳ_ｎとすると、
Ｓ_ｎ＝ａ(１−ｒ^ｎ)／(１−ｒ)となります。

なぜなら、

Ｓｎ	＝ａ	＋ａｒ	＋ａｒ２	＋ａｒ３	＋・・・	＋ａｒｎ−１
ｒＳｎ	＝	＋ａｒ	＋ａｒ２	＋ａｒ３	＋・・・	＋ａｒｎ−１	＋ａｒｎ

このようにＳ_ｎとｒＳ_ｎを並べて書きますが、その際にｒＳ_ｎの各項を １つ右にずらしてかくのがポイントです。
そうすると縦に同じ項が並ぶのです。
従ってここで引き算をすれば、最初と最後の項を残してすべて消えてしまいます。
Ｓ_ｎ−ｒＳ_ｎ＝ａ−ａｒ^ｎ
(１−ｒ)Ｓ_ｎ＝ａ(１−ｒ^ｎ)
となって、Ｓ_ｎ＝ａ(１−ｒ^ｎ)／(１−ｒ)となります。

この公式を確か私は高校２年生で勉強したと思います。
鮮やかに中間の項が消えてなくなるのに、感動した覚えがあります。(やや大げさかな？)

このアイディアは別な場面でも応用できます。
２，４・３，６・３^２，８・３^３，・・・
というように等差数列と等比数列がミックスされたような数列の和を求めてみます。

一般項が、ａ_ｎ＝{ａ＋(ｎ−１)ｄ}ｒ^ｎ−１とします。

Ｓｎ	＝ａ	＋(ａ＋ｄ)ｒ	＋(ａ＋２ｄ)ｒ２	＋(ａ＋３ｄ)ｒ３	＋・・・	＋{ａ＋(ｎ−１)ｄ}ｒｎ−１
ｒＳｎ	＝	＋ａｒ	＋(ａ＋ｄ)ｒ２	＋（ａ＋２ｄ)ｒ３	＋・・・	＋{ａ＋(ｎ−２)ｄ}ｒｎ−１	＋{ａ＋(ｎ−１)ｄ}ｒｎ

ここで先ほどと同様にｒＳ_ｎを１つ右にずらした形で引き算をすれば、

Ｓ_ｎ−ｒＳ_ｎ＝ａ＋ｄｒ＋ｄｒ^２＋ｄｒ^３＋・・＋ｄｒ^ｎ−１＋{ａ＋(ｎ−１)ｄ}ｒ^ｎ

今回は消えてなくなりはしませんが、最初と最後の項を除く中間の項が、単純な等比数列になります。
従ってここからの計算は、以下のようになります。

(１−ｒ)Ｓ_ｎ＝ａ＋ｄｒ(１−ｒ^ｎ−１)/(１−ｒ)＋{ａ＋(ｎ−１)ｄ}ｒ^ｎ

Ｓ_ｎ＝ａ/(１−ｒ)＋ｄｒ(１−ｒ^ｎ−１)/(１−ｒ)^２＋{ａ＋(ｎ−１)ｄ}ｒ^ｎ/(１−ｒ)

これは大げさではなく、高校生だった私はすごいなあ！と思いました。
実は今回の問題２はこのタイプの問題でした。

解答その３の少年Ｈさんは、また別なアイディアで解答していただきました。

E-mail 戻る ホ−ムペ−ジ