係丏嶌恾偺栤戣
廲丄墶丄幬傔丄偳偺曽岦偱傕昩懍侾cm偱摦偗傞儁儞傪 旛偊偨嶌恾憰抲偑偁傞丅 儁儞偑巻偵偮偄偰偄傟偽摦偒偵廬偭偰慄偑昤偐傟丄 儁儞偑巻偐傜棧傟偰偄傟偽壗傕昤偐傟側偄丅 偙偺憰抲偱壓偺恾宍傪昤偔偺偵嵟抁偱壗昩偐偐傞偐丅 偨偩偟丄恾偵尰傟傞妏偼偡傋偰捈妏偲偟丄 儁儞傪巻偵偮偗偨傝棧偟偨傝偡傞摦嶌偵偼 帪娫偼偐偐傜側偄傕偺偲偡傞丅
栤戣偺弌揟
戞俆夞擔杮悢妛僆儕儞僺僢僋梊慖乮侾俋俋俆乯栤戣
乽悢妛僆儕儞僺僢僋侾俋俋侾乣侾俋俋俇乿
擔杮昡榑幮
摎偊偲夝愢
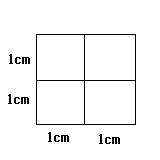
係丏廲丄墶丄幬傔丄偳偺曽岦偱傕昩懍侾cm偱摦偗傞儁儞傪
旛偊偨嶌恾憰抲偑偁傞丅
儁儞偑巻偵偮偄偰偄傟偽摦偒偵廬偭偰慄偑昤偐傟丄
儁儞偑巻偐傜棧傟偰偄傟偽壗傕昤偐傟側偄丅
偙偺憰抲偱壓偺恾宍傪昤偔偺偵嵟抁偱壗昩偐偐傞偐丅
偨偩偟丄恾偵尰傟傞妏偼偡傋偰捈妏偲偟丄
儁儞傪巻偵偮偗偨傝棧偟偨傝偡傞摦嶌偵偼
帪娫偼偐偐傜側偄傕偺偲偡傞丅

夞摎丒偦偺侾
乮儁儞僱亅儉丗暽搒旳堦乯
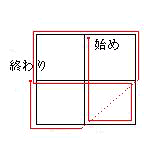
1cm/1sec偲偟偰丄揰慄偺晹暘偼幚嵺偵偼偐偐側偄偲偙傠丄
SQR(2)丅廬偭偰慡懱偱偼12+SQR(2)昩丅
夞摎丒偦偺俀
乮儁儞僱亅儉丗僐儗僋僩僐亅儖偼侾侽俇斣両乯
偙偺嶌恾憰抲偵偍偄偰嵟傕昤偔偺偵揔偟偰偄傞恾宍偼 乽堦昅彂偒偺偱偒傞恾宍乿偱偁傞丅 側偤側傜偽丄乽昤偄偰偄側偄帪娫乿偮傑傝乽儉僟側帪娫乿偑 侽偵側傞偐傜偱偁傞丅
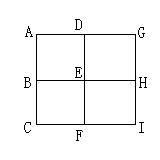
偝偰丄栤戣偺恾偺揰傪俙丄俛丄俠丄俢丄俤丄俥丄俧丄俫丄俬偲偍偔丅
堦昅彂偒偺壜擻側恾宍偺忦審
嘆奺乆偺揰偐傜怢傃偰偄傞慄偺杮悢偑偡傋偰嬼悢偱偁傞丅
嘇怢傃偰偄傞慄偺杮悢偑婏悢偵側偭偰偄傞揰偑俀儢強偩偗丅
嘆嘇偺偄偡傟偐偑惉傝棫偰偽傛偄
巆擮側偑傜丄栤戣偺恾宍偼忋偵宖偘偨忦審偵崌抳偟側偄偺偱丄 堦昅彂偒偼偱偒側偄丅
偦偙偱丄恾宍偵偱偒傞偩偗抁偄慄傪彂偒壛偊丄 堦昅彂偒偺偱偒傞恾宍傪嶌恾偡傞偺偑丄嵟傕崌棟揑偱偁傞丅 乮彂偒壛偊偨慄偺晹暘偼儁儞傪巻偐傜棧偟偰偍偗偽傛偄丅乯
偙偺恾宍偵偼丄慄偑俁杮墑傃偰偄傞揰偑係儢強乮揰俛丄俢丄俥丄俫乯 偁傞偺偱丄偆偪俀儢強傪捈慄偱寢傋偽丄忋偺忦審偺嘇偵崌抳偡傞偺偱丄 堦昅彂偒偑壜擻偵側傞丅 偦偙偱丄偲傝偁偊偢俛俥傪寢傃丄 乮暿偵丄俛俢偱傕俢俫偱傕俥俫偱傕傛偄丅乯偙傟傪揰慄偱昞婰偡傞丅
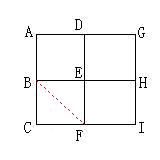
俛俥偺挿偝偼丄俛俠亖俠俥亖侾cm偱偁傝丄 佢俠亖佢俼乮90邅j側偺偱丄 嶰暯曽偺掕棟傛傝SQR(2)cm偵側傞丅 傑偨丄幚慄晹暘偺憤墑挿偼丄峫偊偰傒傟偽傢偐傞偑侾俀cm偵側傞丅
偝偰丄嶌恾憰抲偺儁儞愭傪揰俫偑偔傞埵抲偵偍偔丅 偦偟偰丄壓偵帵偡傛偆偵偨偳傞丅 乮壓恾偵儖亅僩傪柾幃揑偵帵偡丅偙偺懠偵傕嫍棧偺摨偠偵側傞儖亅僩偼偁傞丅乯
俫仺俧仺俢仺俤仺俫仺俬仺俥仺俛仺俠仺俥仺俤仺俛仺俙仺俢
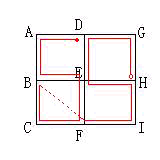
偙傟偑嵟抁儖亅僩偱偁傞丅慜弎傛傝偙偺儖亅僩偺挿偝偼丄12+SQR(2)丂cm
嶌恾憰抲偼侾cm/昩偩偐傜丄12+SQR(2)昩
夞摎丒偦偺俀丒僐儊儞僩
姰帏側儗億亅僩偩偹両丂12+SQR(2)昩偑嵟抁偩偲偄偆棟桼傕偒偪傫偲帵偝傟偰偄傞丅
惓夝幰乮儁儞僱亅儉乯
俛俼俙俬俶俵俙俶俬俙
俲俷倀
俥俴俙俽俫両
杴恖丅
儈僱儔儖丂倂倎倲倕倰
愇愳偛偊傕傫
俙倛両俵倷丂俧倧倓倓倕倱倱
偼側僼儉僼儉
偤偵偑偨偺偲偭偮偁傫
儀僕僞儕傾儞側擏怘廱
俛俙俛倄丂俵俬俶俶俬俤
僒儞僕僃儖儅儞
傑偲傔
堦昅彂偒偺栤戣偩偲偄偆偙偲偑傢偐偭偨偐側丠丂 傕偟丄儁儞傪嵟弶偐傜嵟屻傑偱棧偝偢偵昤偗傟偽乮堦昅彂偒偱偒傟偽乯 堦斣柍懯偑側偄傢偗偱丄 偦偆偡傞偲侾俀昩偱偡丅
偟偐偟丄偙偺恾宍偼堦昅彂偒偱偒傑偣傫偐傜丄侾俀亄兛丅 偙偺兛傪偄偐偵彫偝偔偡傞偐偑栤戣偱偡丅
偲偙傠偱丄堦昅彂偒偲偄偊偽丄乽働亅僯僸僗儀儖僌偺俈偮偺嫶栤戣乿丅
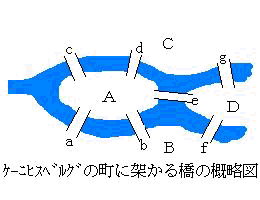
働亅僯僸僗儀儖僌偺俈偮偺嫶栤戣
崱偐傜俀悽婭埲忋傕愄丄僪僀僣偑傑偩僾儘僔儍偲屇偽傟偰偄偨帪戙丄
働亅僯僸僗儀儖僌偺挰偺榖偱偁傞丅
偙偺挰傪棳傟傞僾儗亅僎儖愳偵俀偮偺搰偲偦傟傜傪寢傇俈偮偺嫶偑偁偭偨丅
偙偺俈偮偺嫶偺偳偺嫶傕偪傚偆偳侾夞偢偮搉傞傛偆側嶶曕偺僐亅僗偼
側偄偩傠偆偐丠丂偲偄偆偺偑恖乆偺榖戣偲側偭偰偄偨丅
偙偺栤戣傪夝寛偟偨偺偑丄僗僀僗惗傑傟偺執戝側悢妛幰僆僀儔亅乮1707-1783乯偱偡丅
僆僀儔亅偼偙偆峫偊偨偺偱偡丅
傑偢棨偲搰傪揰偱昞偟丄嫶偼偦傟傜傪寢傇慄偲偡傞丅
偙傟偑壓偺恾偱偡丅偙偺恾偑堦昅彂偒偱偒傞偐偳偆偐偵傛傞丄偲丅
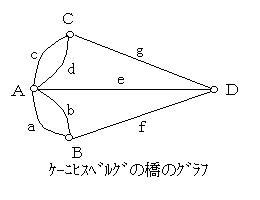
偦偙偱丄偳傫側恾宍偑堦昅彂偒偑偱偒偰丄偳傫側恾宍偑偱偒側偄偐傪尋媶偟偰摼偨偺偑 乽堦昅彂偒偺掕棟乿偱偡丅
偡側傢偪丄奺揰偐傜弌偰偄偔乮or擖偭偰偔傞乯曈偑嬼悢偺偲偒偙偺揰傪嬼揰丄 婏悢側傜偽婏揰偲屇傇丅偦偟偰丄恾宍慡懱偵婏揰偑偄偔偮偁傞偐悢偊傑偡丅 乮婏揰偺屄悢偑婏悢偲偄偆偙偲偼偁傝偊側偄丅 側偤側傜丄侾偮偺曈偼昁偢椉抂偱侾夞偢偮丄偮傑傝俀夞僇僂儞僩偝傟傞偐傜偱偡丅乯
嘆婏揰偑側偄側傜偽偙偺恾宍偼偳偙偐傜彂偒巒傔偰傕堦昅彂偒偱偒傞丅
嘇婏揰偑俀偮偁傞恾宍偼丄偳偪傜偐堦曽偺婏揰偐傜彂偒巒傔傟偽丄 傕偆堦曽偺婏揰偱彂偒廔傢傝丄堦昅彂偒偱偒傞丅
嘊婏揰偑係偮埲忋偁傞恾宍偼偳偆傗偭偰傕堦昅彂偒偱偒側偄丅 働亅僯僸僗儀儖僌偺僌儔僼偼係揰偡傋偰偑婏揰偱偡偐傜晄壜擻偲偄偆傢偗偱偡丅
嘆嘇偺働亅僗偵偮偄偰峏偵晅偗壛偊傞側傜偽丄偳偆傗偭偰傕昁偢堦昅彂偒偱偒傞偲偄偆傢偗偱偼側偔丄
偆傑偄儖亅僩傪偨偳傟偽偱偒傞丄偲偄偆偙偲偱偡丅岆夝偺側偒傛偆丅
偝偰栤戣偵栠傝傑偡偑丄梌偊傜傟偨恾宍偼婏揰偑係偮偁傝丄廬偭偰兛亗侽丅
乮堦昅彂偒偱偒側偄偐傜僱乯
偦偙偱丄俀偮偺婏揰傪寢傇慄暘傪晅偗壛偊偰丄偙偺俀揰傪嬼揰偵曄偊偰偟傑偊偽偄偄偺偩両
(儁儞僱亅儉丗僐儗僋僩僐亅儖偼侾侽俇斣両乯偝傫偺夞摎捠傝偱偡偹丅

 栠傞
栠傞