Weekend Mathematics乛栤戣乛栤戣33
俁俁丏墌偺栤戣

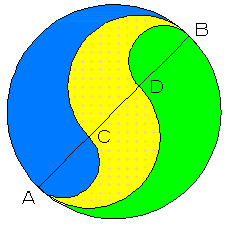
墌偺捈宎俙俛傪俀揰俠丄俢偵傛偭偰俁摍暘偟偰丄
俙俛偺堦曽偺懁偵俙俠偲俙俢傪捈宎偲偡傞敿墌傪昤偒傑偡丅
偦偟偰丄傕偆堦曽偺懁偵俛俢偲俛俠傪捈宎偲偡傞敿墌傪昤偒傑偡丅
偙偺偲偒丄暘偗傜傟偨俁偮偺僄儕傾偺偆偪堦斣柺愊偺戝偒偄偺偼偳傟偱偟傚偆丠丂丂丂
嵍偐傜丄侾斣惵丄俀斣墿怓丄俁斣椢偺偄偢傟偐偱摎偊偰偔偩偝偄丅
擸傔両僷僗儔亅(挧愴偦偺侾)
傾儞僕僃儔丒僼僅僢僋僗丒僟儞曇
孾妛弌斉
乮儁儞僱亅儉丗儅僒儃乕乯
墌偺敿宎傪俁倰偲偟偰丄墌偺敿暘傪侾俉侽夞揮偡傞偲乮棤曉偟偲塢偆偐傕乯
墿怓偺柺愊偼敿宎俀倰偺墌偐傜敿宎倰偺墌偺柺愊傪堷偄偨傕偺偲側傞偺偱丄
墿怓偺柺愊偼丂兾(俀倰)俀亅兾倰俀亖俁兾倰俀
惵偲椢偺柺愊偼摍偟偔丄偦偺柺愊偼慡懱偐傜墿怓偺柺愊傪堷偒丄俀偱妱偭偨傕偺側偺偱
惵丄椢偺柺愊 = {兾(俁倰)俀乕俁兾倰俀乸/俀
= 俁兾倰俀
傛偭偰慡偰偺怓偺柺愊偼摍偟偄丅

乮儁儞僱亅儉丗奀捗杒崅峑侾擭俀慻慡堳乯
俙俛亖俇們倣偲偍偔丅
敿宎俁們倣偺戝墌偺柺愊偼丄俁亊俁兾亖俋兾
敿宎俀們倣偺拞墌偺柺愊偼丄俀亊俀兾亖係兾
敿宎侾們倣偺彫墌偺柺愊偼丄侾亊侾兾亖兾
傛偭偰丄
| 嘆偺柺愊偼丄 | 丂侾乛俀乷乮戝墌乯亅乹拞墌乯亄乮彫墌乯乸 |
| 亖侾乛俀乷俋兾亅係兾亄兾乸 | |
| 亖俁兾 | |
| 嘇偺柺愊偼丄 | 丂乷乹拞墌乯亅乮彫墌乯乸 |
| 亖係兾亅兾 | |
| 亖俁兾 | |
| 嘊偺柺愊偼丄 | 丂侾乛俀乷乮戝墌乯亅乹拞墌乯亄乮彫墌乯乸 |
| 亖侾乛俀乷俋兾亅係兾亄兾乸 | |
| 亖俁兾 |

乮儁儞僱亅儉丗彫弔乯
偙傟偼慡晹摨偠戝偒偝偱偼側偄偺偱偟傚偆偐丠
恾偺彂偒曽偑暘偐傜側偄偺偱慡晹尵梩偱彂偐偣偰傕傜偄傑偡丅
傑偢丄栤戣偺恾偺俙俛偺忋敿暘偩偗傪峫偊傑偡丅
敿墌俛俢偺柺愊傪侾偲偍偔偲丄曈偲柺愊偺憡帡斾偐傜敿墌俛俠丄敿墌俛俙偺柺愊
偼偦傟偧傟係丄俋偵側傞偺偱丄
椢丄墿丄惵偺柺愊偼偦傟偧傟侾丄俁丄俆偲側傝傑偡丅
偙傟偱壓敿暘偺柺愊傕摨偠側偺偱丄
寢嬊俁偮偺柺愊偼偡傋偰俇偵側傝傑偟偨丅丂

乮儁儞僱亅儉丗sambaGREEN乯
俁偮偺敿墌偺捈宎偺斾偼侾丗俀丗俁丅廬偭偰柺愊斾偼侾丗係丗俋
捈宎俙俛偺嵍忋偺晹暘偺丂椢丗墿丗惵亖侾丗俁丗俆
捈宎俙俛偺塃壓偺晹暘偺丂椢丗墿丗惵亖俆丗俁丗侾
備偊偵丆柺愊偼偡傋偰摍偟偄丅

乮儁儞僱亅儉丗偪傖傔乯
傑偢捈宎傪擟堄偵俁偮偵暘妱偡傞応崌傪峫偊傑偡丅
墌偺捈宎AB傪俀偲偡傞丅
AC=2a, BD=2b, CD=2c 偲偡傞丅
0亙a, b, c亙1丂丂a+b+c=1丂丂偱偁傞丅
嵍惵丄拞墰墿丄塃椢偺柺愊傪偦傟偧傟B, Y, G偲偡傞丅
墌廃棪傪兾偲偡傞偲丄
恾偐傜丄
2B/兾 = 12-(1-a)2+a2=2a
B=a亊兾
摨條偵丄
G=b亊兾
傑偨丄
2Y/兾 = (a+c)2-a2 + (b+c)2-b2 = 2c亊(a+b+c)=2c
傛偭偰丄
Y=c亊兾
埲忋偐傜丄
B : Y : G = a : c : b = AC : CD : BD
偡側傢偪柺愊斾偼捈宎傪暘偗傞斾偵摍偟偄丅
傛偭偰俠丄俢偑俁摍暘揰偱偁傞応崌偼丄
俁偮偺僄儕傾偺柺愊偼偡傋偰摍偟偄丅
乮摎偊乯丂惵丄墿丄椢偄偢傟傕嵟戝偱偁傞丅乮偄偢傟傕嵟戝偱側偄丠乯

乮儁儞僱亅儉丗偐偵乯
AB=r, AC=r1, CD=r2, DB=r3 偲偡傞偲
(r1+r2+r3=r)
惵怓偺僄儕傾偺柺愊偼
| 1/2兾(r/2)(r/2)-1/2兾(r2+r3/2)(r2+r3/2)+1/2(r1/2)(r1/2) | |
| = | 1/8兾r亊r-1/8兾(r-r1)(r-r1)+1/8兾r1亊r1 |
| = | 1/4兾r亊r1 |

乮儁儞僱亅儉丗悈偺棳傟乯
愭擔丆嶲娤庼嬈偱崱寧偺栤戣傪庢傝埖偄傑偟偨丅
摎偊傪幨恀偱憲傝傑偡丅偛棗偔偩偝偄丅
俁偮偺僄儕傾偺宆巻傪嶌偭偰丆廳偝傪應偭偰丆挷傋傑偟偨丅

愭惗偑丄宆巻俁庬椶傪帩偭偰偒偰暿偺峫偊曽偼側偄偐偲幙栤偟傑偟偨丅
嫵戩偵偼丄揤攭偑抲偄偰偁偭偨偺偱丄偍傕偝傪偼偐偭偰偍偍偒偝傪挷傋傑偟偨丅
椢偲墿怓偼摨偠廳偝偱丄崱搙偼惵偲墿怓傕摨偠廳偝側偺偱丄
俁偮偺僄儕傾偺戝偒偝偼慡偰摍偟偄丅
奀捗杒崅峑侾擭俀慻壠惌壢慡堳



| 悈偺棳傟 | 偐偵 | 偁傝偝偺偍晝偝傫 |
| 奀捗杒崅峑侾擭俀慻慡堳 | 昹揷丂柧枻 | sambaGREEN |
| 偐偹偝傫 | 傕偺傕偺 | 儅僒儃亅 |
| Idaho Potato | 寧偺岝 | 彫弔 |
| 偪傖傔 | toki |


摉弶俁摍暘偲偄偆偲偙傠偑濨枂側昞尰偱丄偛柪榝傪偍偐偗偟傑偟偨丅
摍暘偱偼側偔丄堦斒偵俁暘妱偟偨傜偳偆側傞偐偲偄偆夝摎傪偍傛偣偄偨偩偒傑偟偨丅
(夝摎丒偦偺俆偺乽偪傖傔乿偝傫丄夝摎丒偦偺俇偺乽偐偵乿偝傫)
偦傟偵傛傞偲丄捈宎傪暘妱偡傞偲偒偺挿偝偺斾偑丄偦偺傑傑柺愊斾偵側傞偺偱偡偹丅

巹偼傑偨堘偭偨堄枴偱堦斒壔偟偰傒傛偆偲巚偄傑偡丅
摍暘偵暘妱偡傞丄偦偺暘妱悢傪堦斒壔偟偰傒傑偟偨丅
傑偢偼係摍暘偐傜丅
捈宎傪係摍暘偟偰摨偠傛偆偵係偮偺僄儕傾偵暘偗傑偡丅
敿墌偺柺愊斾偼彫偝偄曽偐傜侾丗俁丗俆丗俈偲側傝傑偡丅
偙傟傪媡岦偒偵慻傒崌傢偣偰懌偟傑偡偺偱丄
侾亄俈亖俉丄俁亄俆亖俉丄俆亄俁亖俉丄俈亄侾亖俉偲偡傋偰摍偟偔側傝傑偡丅

俆摍暘偱傕摨條偱偡丅
敿墌偺柺愊斾偼彫偝偄曽偐傜侾丗俁丗俆丗俈丗俋偲側傝傑偡丅
俆偮偺僄儕傾偺柺愊斾偼侾侽丗侾侽丗侾侽丗侾侽丗侾侽偲偡傋偰摍偟偔側傝傑偡丅
偙傟偼執戝側悢妛幰僈僂僗偺梒偄崰偺僄僺僜亅僪傪巚偄弌偟傑偡丅
巕嫙偨偪偵乽侾亄俀亄俁亄丒丒丒亄侾侽侽乿偺寁嶼傪壽偟偰帺暘偼偺傫傃傝偟傛偆偲偟偨
價儏僢僩僫亅愭惗偼丄傑傕側偔僈僂僗彮擭偐傜乽俆侽俆侽乿偲偩偗彂偐傟偨
愇斅傪庴偗庢傞偙偲偵側傝傑偡丅
偳偆傗偭偰摎偊傪偩偟偨偺偐丠丂偲栤傢傟傞偲僈僂僗彮擭偼偙偆摎偊偨偺偱偡丅
乽侾侽侽亄侾亖侾侽侾丄俋俋亄俀亖侾侽侾丄俋俉亄俁亖侾侽侾偲偄偆傆偆偵俀偮偯偮懌偟傑偡丄
偙傟偑侾侽侽偺側偐偺懳偩偗偁傝傑偡偐傜丄摎偊偼俆侽亊侾侽侾偮傑傝俆侽俆侽偱偡丅乿
堦斒偵墌傪値摍暘偟偰摨偠傛偆偵値屄偺僄儕傾偵暘偗偨偲偟傑偡丅
敿墌偺柺愊斾偼彫偝偄曽偐傜侾丗俁丗俆丗丒丒丒丗(俀値亅侾)偲側傝傑偡丅
嵍偐傜倝斣栚偺僄儕傾偺柺愊偼丄
(2i-1)+{2(n+1-i)-1}=2n
偲側傝丄倝偵柍娭學側抣偲側傝傑偡丅偮傑傝偡傋偰偺僄儕傾偺柺愊偼摨偠偲偄偆偙偲偱偡丅
偲偙傠偱丄敿墌偺柺愊斾偑
侾丗(係亅侾)丗(俋亅係)丗(侾俇亅俋)丗(俀俆亅侾俇)亖侾丗俁丗俆丗俈丗俋
偲偄偆傛偆偵婏悢偑暲傇偺偼側偤偱偟傚偆丠
(嬼慠偱偼側偄偺偩傛両)
値俀亅(値亅侾)俀亖俀値亅侾
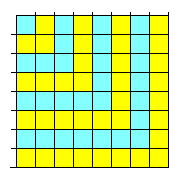
値斣栚偺暯曽悢偲(値亅侾)斣栚偺暯曽悢偲偺嵎偼値斣栚偺婏悢偵側傞偺偱偡丅
嵍偺恾傪尒偰偄偨偩偄偰傕傢偐傞偐側丠(嵍忋偐傜塃壓偵岦偐偭偰尒偰偔偩偝偄丅)
傑偨媡偵偄偆偲丄婏悢傪弴偵懌偟偰偄偔偲偦傟偼忢偵暯曽悢偩偲偄偆尵偄曽傕偱偒傑偡偹丅
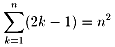 丂偲偄偆傢偗偱偡丅
丂偲偄偆傢偗偱偡丅
 栠傞
栠傞