Weekend Mathematics／問題／問題30

３０．多角形の問題

最小の内角が１２０度で、それにつづく内角がどれもその前の角より５度だけ大きい ような多角形は２つだけです。ひとつは右に描かれている九角形です。 もうひとつは何角形でしょうか？

解答・その１

（ペンネ−ム：さだやん）

外角の和が360度になるように内角をとればいい。
60+55+50+45+40+35+30+25+20＝360------------9角形
（60+55+……………+25+20）+15+10+5+0+（-5）+（-10）+（-15） =360--------------16角形

感想
作図で考えようかと思いました。 でも，はじめできないと思いました。 できるとすると180度より大きくなる角を使いそうですが， すると最後は鋭角になるようでできない。
ふと，外角の和が360度になればいいのだ。と気づきました。 負の外角？も許すと機械的にできました。

解答・その２

（ペンネ−ム：荒城　清美）

求める多角形をｎ角形とする。

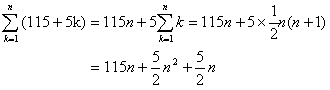
これは１８０×(ｎ−２) と等しいので

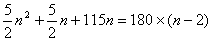
5n²-125n+720=0
n²-25n+144=0
(n-9)(n-16)=0
∴ n=9,16
ゆえに９角形と１６角形である。

《翌日のmail・・・》
ここで、多角形であるためには角が１８０度より小、 すなわちｎ＜１３でなければならない。 ｎ＝１６ はこれを満たさないので題意を満たす多角形は ９角形しかない。（？？？）

《数日後のmail・・・》
しかし、１６角形をかいていくと途中で１８０度が出てきてしまう。 そうするとこれは１６角形ではない。だからといって１５角形とすると 矛盾する。したがって条件に合う多角形は９角形しかない。（？？？）

解答・その３

（ペンネ−ム：数楽者）
今月の問題ですが、頂点数が１３以上になると、 内角が180度の頂点？が出来ますがいいのでしょうか。 頂点数に関する２次方程式を解くと１６角形となりますが 少し心配です。

《数日後のmail・・・》

多角形の問題の答 　　　７角形
角度は順に、135,130,125,120,125,130,135です

略解
１２０度から両側に５度づつ増やしていき、 外角の合計が３６０度になった所で終わります。
両側の角が同じになっている必要はありませんが、 今回の答は偶然？そうなっていました。

解答・その４

（ペンネ−ム：kiyo）

初項が１２０で公差が５の等差数列は、 ５ｎ＋１１５　(ｎは自然数。)
初項からｎ項までの和は、
（５ｎ^２＋２３５ｎ）／２・・・・・・・・（１）
またｎ角形の内角の和は、
１８０ｎ−３６０・・・・・・・・・・・（２）
（１），（２）が等しい。
（１），（２）から
ｎ^２−２５ｎ＋１４４＝０
（ｎ−９）（ｎ−１６）＝０
ｎ＝９　または　ｎ＝１６
したがって、求めるもうひとつの多角形は１６角形となる。
　　　　　　　　　　　　　　　　　　　　　　　答え　１６角形。

《数日後のmail・・・》
先日の解答で１６角形としましたが、内角が１８０度となるところがあります。 題意を満たさなくなるのではと思うのですが。
１２０，１２５，１３０，１３５，１４０，１４５，１５０，１５５，１６０，１６ ５，１７０，１７５，１８０ １８５，１９０，１９５。
凸型多角形と凹型多角形を問う問題ではないかと思います。
例えば、１１７．５が最小の内角であれば、８角形と１８角形は可能だと思います。

• １１７．５，１２２．５，１２７．５，１３２．５，１３７．５，１４２．５，１４ ７．５，１５２．５
  内角の和　１０８０度　１８０×（８−２）＝１０８０
  
  
• １１７．５，１２２．５，１２７．５，１３２．５，１３７．５，１４２．５，１４ ７．５，１５２．５ １５７．５，１６２．５，１６７．５，１７２．５，１７７．５，１８２．５，１８ ７．５，１９２．５ １９７．５，２０２．５
  内角の和　２８８０度　１８０×（１８−２）＝２８８０
  
  

《数日後のmail・・・》

1. １２０度を起点に同一方向に５度づつ増える場合。
   
   （５ｎ^２＋２３５ｎ）／２＝１８０×（ｎ−２）
   ｎ^２−２５ｎ＋１４４＝０
   （ｎ−９）（ｎ−１６）＝０
   ｎ＝９　または　ｎ＝１６
   ｎ＝１６のとき
   １２０，１２５，１３０，１３５，１４０，１４５，１５０，１５５，１６０， １６５，１７０，１７５，１８０，１８５，１９０，１９５
   １３番目が１８０度となり不適。
   
   
2. １２０度を起点に時計回りと反時計回りに５度づつ増える場合。
   
   （５ｍ^２＋２４５）／２＋（５ｎ^２＋２３５ｎ）＝１８０×（ｍ＋ｎ−２）
   ｍ^２−２３ｍ＋ｎ^２−２５ｎ＋１４４＝０
   （ｍ−１１．５）^２＋（ｎ−１２．５）^２＝（１７√２）／２）^２
   ｍ、ｎが自然数であるとき、
   ｍ＝８，ｎ＝１　または　ｍ＝３，ｎ＝４
   前者の場合は９角形。後者の場合は７角形。
   

   　　　　　　　　　　１２０
   　　　　　　　　１２５　　　１２５
   　　　　　　　１３０　　　　１３０
   　　　　　　　　１３５　１３５
   

   内角の和９００度。１８０×（７−２）＝９００
   題意を満たす。したがってもうひとつの多角形は７角形となる。
   

解答・その５

（ペンネ−ム：ありさのお父さん）

最初は、単純にExcelに

180		120
360	540	125	245
540	1080	130	475

と言った具合に、凸型多角形と、120°からの内角の合計を計算し、 ぐいっと下へ引っ張り（Excelを使わない人にはわかりにくい言い方で、 すみません。繰り返し計算です。）、 合計が同じになる数字を探して、 9と16が答えと思いました。

式を解いても
(n-2)×180 = 115n+5×(1+2+.....+n)
180n-360 = 115n+5×n(n+1)/2
(n-16)(n-9) = 0 になります。
でも、内角が180°以上とはいったいどういうこと と悩みはじめました。凹型を認めても、内角が180°の 頂点があるわけがないしと.....。

その後、しばらくたってから問題文を読み直し、 両側へ角度が大きくなってもいいと気づきました。
あとは、またExcelで、 180-内角の合計を次のように計算して、

120	60
125	55	115
125	55	170
130	50	220
130	50	270
135	45	315
135	45	360

で360°になってめでたしめでたしです。
答えの多角形を図にしましたので、添付します。

《数日後のmail・・・》
(n-2)×180 = 115n+5×(1+2+.....+n)
180n-360 = 115n+5×n(n+1)/2
(n-16)(n-9) = 0
から，９角形か１６角形になりますが， これを作図すると添付ファイルのようになります。
ここで，内角が１８０度の点 N は多角形の頂点とは呼べないんで， これを除いて数えるべきだと思います。

と言うことで，　　答え　１５角形

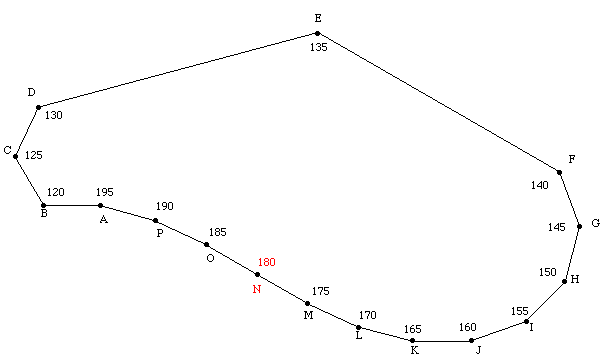
(この図もご本人の提供です。)

解答・その６

（ペンネ−ム：ヨッシー）

該当する多角形がｎ角形だとすると、 その内角の和は 180(n-2) 度。
一方、問題の条件より、内角の和は

　120+125+・・・・+{120+5(n-1)}
　　＝120n+5{0+1+・・・・+(n-1)}
　　＝120n+5n(n-1)/2

解答・その７

（ペンネ−ム：ものもの）

１２０゜の角を作って片方の辺を基準にします。（０゜）。
点が進んでいってそして曲がるとすると１２０゜の次は１２５゜なので ５５゜左に曲がります、次は１３０゜なので５０゜曲がります、 以下同様です（１８５゜からは右曲がり）。
そして、それらの曲がる角度を順次足していくと、 Ｎ回曲がった時の辺の基準からの角度になります。
基準から１２０゜で平行、それから１８０゜曲がると基準でない もう一方の辺とつながることがわかります。 つまり３００゜でつながります。
曲がる角度を順次足していくと
５５゜＋５０゜＋４５゜＋４０゜＋３５゜＋３０゜＋２５゜＋２０゜ （ここで３００゜になる。ここまで８回曲がっている、 最初の１２０゜の角を足して９角。）
＋１５゜＋１０゜＋５゜＋０゜ （ここは１７５゜の次なので１８０゜として、角にはならないが点だけ打つ。 角には数えないが１８０゜の角とみなす？）
ー５゜（ここから右曲がりなのでマイナス）
ー１０゜ー１５゜（ここで３００゜、１４回曲がりなので１５角）
よって９角形と１５角形が可能です。

発展・その１

（ペンネ−ム：Chee）

問題の多角形をN角形とする。
それぞれの内角をたしていくと、
120 + (120+5) + ... + 120+5×(N-1)= 120×N + 5×(N-1)×N/2
一方、N角形の内角の和は、180×(N-2)なので、
120×N + 5×(N-1)×N/2 = 180×(N-2)
整理して、 N² - 25×N + 144 = (N - 9)×(N-16) = 0
答えは、９角形と１６角形。

ちなみに、最小の内角をa度とした場合は、
それぞれの内角をたしていくと、
a + (a+5) + ... + a+5×(N-1)= a×N + 5×(N-1)×N/2
一方、N角形の内角の和は、180×(N-2)なので、
a×N + 5×(N-1)×N/2 = 180×(N-2)
整理して、 N² + (2/5×a - 73)×N + 144 = 0、（0＜a＜180）
(2/5×a - 73)をAとおいて、無理矢理Nについて解くと

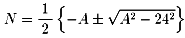
Nは整数なので、ルートの中身：(A² - 24²)は平方数になる。
ところで、0＜a＜180だったので、 -73＜A＜-1。
つまり、1²＜A²＜73²
結局、ルートの中身が平方数になるのは、

• A = -51（a = 55)のとき、N = 48,3
• A = -40（a = 82.5) のとき、N = 36, 4
• A = -30（a = 107.5)のとき、N = 24,6
• A = -26（a = 117.5)のとき、N = 18,8
• A = -25（a = 120) のとき、N = 16, 9
• A = -24（a = 122.5)のとき、N = 12

《数日後のmail・・・》

これをみて、気づいたことがあります。
Ｎの値を見ると、 ３，４，６，８，９，１２，１６，１８，２４，３６，４８と、
すべて「２ⁱ ×３^j (0≦i, 0≦j)」の形をしています。 （当然、(0,0)と(1,0)は除きますが）
すべてそうなのかという予想ができますが、２７（３^３）がありません。
そこで、Ｎ＝２７を確認してみました。
Ａ＝−９７/３（ａ＝７９０/３）となりますが、なんと、これがＯＫなのです。
そこで、「(A² - 24²)は平方数になる。」の部分は、 整数ではなく、有理数まで拡張した平方数にしなければいけないことに気づきました。 （実は気づいていたのですが、まさかＮは整数になるような有理数があるとは．．）
さらに、３２（２^５）もないので、確認してみると、 Ａ＝−５５/２（ａ＝１００５/４）で、これもＯＫ！
これで、すべてのＮが、「２ⁱ ×３^j (0≦i, 0≦j)」であらわせました。
ただし、凸型の多角形（言い方合ってますか？）になる範囲という条件があります。
さて気になることがいくつかあります。
その１：
この性質は、５度づつという条件からきてるのか？
「５度づつ」を変えるとどうなるか？

その２：
今回は、「２ⁱ ×３^j (0≦i, 0≦j)」から抜けを見つけましたが、 「(A² - 24²)は平方有理数になり、Nが整数になる」でちゃんと調べると、 ほかにも見つかるのでは？

その３：
４８より後ろは、多分、内角(?)が１８０度をを超えてしまいますが、実は、 三日月の形のような多角形になるのでは？ これが言えるとすると、どこままでも大きくできるのかな？

《数日後のmail・・・》

冷静に考えてみると、

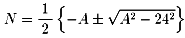
が整数になるには、Ａについて解けばよく、結果は、 Ａ＝−(Ｎ＋１４４/Ｎ)ですね。
つまり、任意のＮでＯＫです。 （どこでどう勘違いしたのか？？？）
で、Ａが整数になるＮはというと、 １４４＝２⁴×３²なので、
Ｎ＝２ⁱ ×３^j(０≦i≦４、０≦j≦２、３≦Ｎ） となります。
ところで、Ａは、「(2/5)×a-73」を置き換えたものなので、Ａが整数 であっても面白くありません。 そこで、ａが整数になるように考えてみました（懲りずに）。
ａ＝(５/２)×(７３−Ｎ−１４４/Ｎ) が整数．．
（５と１４４に注目すると）Ｎの必要条件は、
Ｎ＝２ⁱ ×３^j×５^k （０≦i≦４、０≦j≦２、０≦k≦１、３≦Ｎ）
あとは、この３０個のＮに対して確認するのが手っ取り早いかな。
結果：

• Ｎ(i,j,k)＝(1,3,1)＝３、ａ＝５５
• Ｎ(i,j,k)＝(1,1,5)＝５、ａ＝９８
• Ｎ(i,j,k)＝(1,9,1)＝９、ａ＝１２０
• Ｎ(i,j,k)＝(1,3,5)＝１５、ａ＝１２１
• Ｎ(i,j,k)＝(16,1,1)＝１６、ａ＝１２０
• Ｎ(i,j,k)＝(1,9,5)＝４５、ａ＝６２
• Ｎ(i,j,k)＝(16,3,1)＝４８、ａ＝５５

発展・その２

（ペンネ−ム：ちゃめ）

最初、最小の内角１２０度の角はひとつだけ、と考えてｎ角形について、

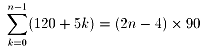
よりn=9,16で１６角形か、と単純に思ったのですが、 １８０度が含まれるので不適なことに気づきました。
で、１２０度の角は複数連続してあってよく、 それにつづく内角が（存在すれば、）どれもその前の角より５度大きい、 というように問題文を解釈しました。
果たしてそれでよいのかどうか解りません。 全然自信がないのですが解答してみます。

---------- 解答 ---------
１８０度は多角形の内角の大きさとしては不適だから、 題意を満たす多角形の内角の大きさは高々１７５度である。
１２０度の内角ｋ個、それに続く内角が120+5×1度、120+5×2度、・・・、(120+5m)度 である(k+m)角形を考える。
120≦120+5m≦175 より、mは0≦m≦11の整数。
この多角形の内角の和は、

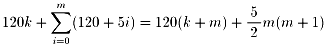（度）

また(k+m)角形の内角の和は、 (2×(k+m)-4)×90=180×(k+m)-360　（度）
よって、この多角形が題意を満たすための必要条件として、
120×(k+m)+(5/2)×m(m+1)=180×(k+m)-360
整理して、 m(23-m)=24(6-k)　・・・(1)
m, 23-m, 6-k は整数だから、 0≦m≦11で(1)を満たす(m,k)の組は (m.k)=(8,1),(0,6) の２組。

• (m,k)=(8,1)のときが問題に示された９角形。
• (m,k)=(0,6)のときは、正６角形になる。

120度以外の角も複数あり得る場合を考えてみました。
内角が120度、125度、・・・、120+5n度から成る多角形で、 どの大きさの内角も複数あってもよい場合を考える。
120+5×m 度の角がＫ_m個あるとする。(0≦m≦11)
{Ｋ_m｝の満たすべき条件として、 Ｋ_m=0となるmの最小値をMとすると、 M≦mであるすべてのmについてＫ_m=0でなければならない。（＊）
内角の総和は、

12+11+・・・+4=72だから、条件（＊）より、 K₉=K₁₀=K₁₁=0　。

• Ｍ=9のとき、(A)の解は Ｋ_m=1 (m=0,1,・・・,8)
  これは問題に示された９角形。
  
  
• M=8のとき、(A)は解なし。
  
  
• M=7のとき、(A)の解は、K₃=2， Ｋ_m=1 (m=0,1,2,4,,5,6)
  （120, 125, 130, 135, 135, 140, 145, 150度の内角を持つ８角形。）
  
  
• M=6のとき、(A)の解は、
  Ｋ_m=1 (m=0,1,2,3), Ｋ_m=2 (m=4,5)
  （120, 125, 130, 135, 140, 140, 145, 145度の内角を持つ８角形。）
  
  
• M=5のとき、(A)の解は、
  Ｋ_m=1 (m=1,3,4), Ｋ_m=2 (m=0,2)
  （120, 120, 125, 130, 130, 135, 140度の７角形。）
  および、 Ｋ_m=1 (m=0,2,3,4), Ｋ₁=3
  （120, 125, 125, 125, 130, 135, 140度の７角形。）
  
  
• M=4のとき、(A)の解は、
  Ｋ₀=1, Ｋ_m=2 (m=1,2,3)
  （120, 125, 125, 130, 130, 135, 135度の７角形。）
  および、 Ｋ_m=1 (m=0,1,3), Ｋ₂=4
  （120, 125, 130, 130, 130, 130, 135度の７角形。）
  
  
• M=3, M=2のとき　(A)は解なし。
  
  
• M=1のとき、(A)の解は、
  Ｋ₀=6 （正６角形。）
  
  

え−っ、そんなのなしだよ・・・、本当に数学の問題？という声が聞こえてきそうな・・・・。
最初にあやまってしまおう、ごめんなさい。

私自身は、「１６角形」という答えを出しました。 出典の本によれば、
「１６角形。ただし、１３番目の角度が、 120+5(13-1)=180(度) になっています。つまり、この１６角形は内角のうちのひとつが１８０度という特別な １６角形ということになりますが、それを私たちは普通、１５角形と呼んでいます。 ですから、答えは１５角形」
ということで、これを読んだ私は思わず笑ってしまいました。

問題文の解釈が、別れるところかもしれません。 数学では、曖昧な表現や定義はまずいわけで、そのあたりを責められるとちょっとつらいところです・・・。
まず、凸多角形に限定すべきかどうか？
問題文を読む限りでは、多角形とあるだけですから、凹多角形(180度以上の角を有する多角形) でもいいと思います。つまり、内角は180度を越えてもいい、と判断できます。 ただし、今回の問題は120度から5度ずつ増やしていくので、その課程で180度という角を通過します。 これを角と認めていいのかどうか？　という疑問は残ります。 実際、ここでためらった方も多いのではないでしょうか？
これを角と認めるなら１６角形(?)、認めないと１５角形(?)、でも認めないと 等差数列にならない？？
混乱を招いてすいません・・・。今回は何回かに渡ってmailをいただいた方々もいます。 どうもありがとうございました。

私の予想外に、７角形という解答がありました。(kiyoさん、数楽者さん、ありさのお父さんさん)
これは120度から5度ずつ増やしていく際に、１方向だけでなく両方向へ増やしていってもいい、 という解釈です。 改めて問題文を読んでみると、それはいいように思います。 じかもその条件に合う多角形が存在する！

また、同じ大きさの角が重複してもいいという解釈(ちゃめさん)がありましたが、 これはご本人がおっしゃるようにちょっと無理があるかな、と思います。 ただこの問題を離れて考えれば、こういった考察は意味があると思います。 今回、発展という形で載せさせていただきました。

また、スタ−トの角度を120度に限定しない(ただし、整数)で考えるとどんな多角形ができるかな？　という レポ−トをくださった方(Cheeさん)もいらっしゃいました。
こういった発想で臨むと、問題作成者の意図がわかってきたりしますね。

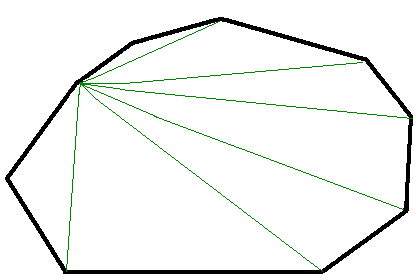
ところで、多角形の内角の和についてです。
Ｎ角形の内角の和は、180(N-2)となります。 それは、(N-2)個の三角形に分割できることから、わかります。
右の図は９角形で、７つの三角形に分割できます。

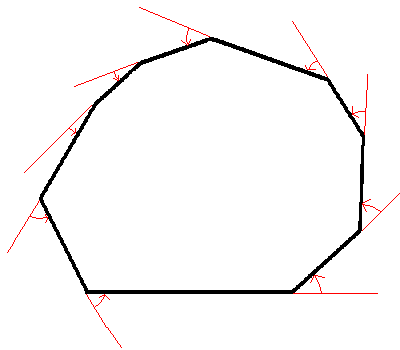
また、外角で考えてくださった方もいます。(さだやんさん、数楽者さん、ものものさん、ありさのお父さんさん)
外角については、どんな多角形でも360度になります。
右の図を見て、多角形に沿って一周してみてください。 外角の和が360度になるのがわかります。

ところで問題にある９角形の図の角度は、正確ではありません。
さすがに１５角形は特に角度を正確に、と思っていました。 角度を正確に描くための道具を持ち合わせていないので、 仕方ない分度器＋スキャナ−？　と思って(ちょっと情けない？)、 分度器を探すべく机の中をがさごそしていました。 そんなある日「ありさのお父さん」さんから、見事な１５角形の図が送られて来ました。 おかげで、私は分度器と格闘せずにすみました。 ご協力に感謝！！

戻る