Weekend Mathematics/問題/問題22
22.時計の問題 正午から夜中の12時までの間に、長針が短針の上を通りすぎるのは
何回でしょうか? ある時計が6時(ポン、ポンと6個)を打ち終わるのに5秒かかります。
では、12時を打ち終わるには何秒かかるでしょう。
ヘンリ−伯父さんが、大変くたびれたので9時に床に入り、
翌朝10時に鳴るように目覚まし時計をセットし、
20分後に眠りました。
目覚まし時計で起こされたときの伯父さんの睡眠時間は?
別冊サイエンス ひらめき思考
マ−チン・ガ−ドナ−
日経サイエンス社
(ペンネ−ム:Hungry Bear)
先ず、最初の1時間(正午から1時まで)は長針は短針には追い付かない
1時から11時までは、1時間ごとに1回ずつ通り過ぎる........
10回
11時からは12時に追い付いて重なるだけで、通りすぎはしない
*3針式の時計の場合手前から秒針.長針.短針の順ですが、
長針と短針が逆になった時計があれば(見たことはないですが)
長針が短針の上を通り過ぎることは1度もありません。
(ペンネ−ム:水の流れ)
11回ですか?
いいえ、10回に訂正します。
<解説>角度で考えます。長針は1分に6度、短針は1分に
0.5度動きます。そこで、m時t分に通り過ぎたとします。
6t=0.5t+30m
ゆえに、t=(60/11)m (m=1,・・・、11)
ところが、m=11のとき、12時になってしまい、
重なりますが、通りすぎません。
したがって、10回です。
(ペンネ−ム:マサボー)
正午から1時と11時から12時の間は、
長針が短針の上を通りすぎることはなく、
それ以外(1→2,2→3,...10→11)
は通り過ぎるので、全部で10回。(グラフを書くと明らか)。
直接時間と求めると
短針、長針と12時のなす角をθ、θ’とすると
θ = 30n+t/2, θ’= 6t
(n=0,1,2,.....,11. tは分で0≦t≦60)。
θ=θ’として、30n+t/2= 6t 、→ t=60n/11
n=0, t=0 → 12時
n=1, t=60/11(≒5.45)→ 1時5.45分
n=2, t=120/11(≒10.9)→ 2時10.9分
....
n=11, t=60→ 12時
よってn=1,2,3,....10の10回
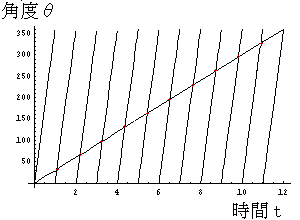
それではというわけで、グラフを書いてみました。
短針のグラフ θ=30tと、
長針のグラフ θ=360(t−[t])
が
10回交わっているのがわかりますか?
それでは、長針、短針、秒針すべてが重なる瞬間が
0時(12時)just以外にあるでしょうか?
結論から言うとありません。
短針と長針が重なるのは、時刻tとして、
範囲0時0分0秒≦t<12時0分0秒の中に11回あります。
(等号に注意! 0時justを入れます。)
従って、一周360°を11等分した箇所で重なります。
(「水の流れ」さんや、
「マサボー」さんが方程式を解いて出してくださっています。)
同様に長針と秒針の重なりを考えます。
秒針は長針の60倍のスピ−ド(角速度)で回転しますので、
長針が1周する1時間の間に、長針と秒針は59回重なります。
重なる場所は、一周360°を59等分した箇所です。
ところが、一周360°を11等分した箇所と59等分した箇所で、
重なる場所は0°しかありません。
なぜなら、11と59の公約数が1以外にはないからです。
(ペンネ−ム:Nagahiro)
11秒
1回目に鳴ってから6回目に鳴るまで5秒だから
その間隔は5÷(6ー1)=1秒。
だから12回鳴り終わるまでにかかる時間は12−1=11
(ペンネ−ム:ネットOL)
11秒
これはけっこう有名ですよね。エレベータ問題と一緒ですね。
(ペンネ−ム:Hungry Bear)
時報を6回打つための間隔は、5つ..これが5秒かかるので
1秒間隔で鳴ることになる。
12回鳴らすための間隔は、11すなわち11秒かかります
*当然鳴っている音の長さは、0秒とするわけですよね。
また、うちの時計は、光センサーが付いていて、
夜暗くなると音が鳴りませんが...
(ペンネ−ム:マサボー)
今、鐘と鐘の間(ポンとポンの間)とtとし、鐘の余韻をΔtとする。
6時を打ち終わる時間は5t+Δtで5秒、
すなわち5t+Δt=5が成り立ち、
Δt=5(1ーt)>0より、tは0<t<1を満たす値。
今、求める時間(12時を打ち終わる時間)をTとすると、
T=11t+Δt=6t+5
よって求める時間は5<T<11となり、
5秒以上(5秒は含まない)、11未満。
但し、tが0あるいは1に近い値をとるとき、時計として機能するは不明。
エレベ−タ−、階段、そうです、そうです。
間隔が問題なのです。
ちょうど今、授業で数列を扱っています。
初項a、公差dの等差数列の一般項は、
an=a+d(n−1)となります。
この初項aに公差dを(n−1)個たすというのは、
初項と第n項との間隔が(n−1)個だからですよね。
(ペンネ−ム:マサボー)
一般的に考えて9時は夜の9時で、眠りに入ったのは9時20分で、
起きたのが10時より、睡眠時間は12時間40分?
(ペンネ−ム:2年4組情報処理科)
一般に考えて、12時間40分と考えたクラスメイトは大半でしたが、
この目覚まし時計はアナログとすれば
夜中の10時にヘンリー伯父さんは起こされるので、
睡眠時間は40分、
デジタルと考えて、午前と午後を区別できれば、12時間40分です。
(ペンネ−ム:Nagahiro)
40分
10時に目覚しを合わせたので、
午前10時に目覚し時計が 鳴り響く以前に午後10時に鳴るので
9時20分に眠りについてから 40分しか寝られない。
24時間用の目覚し時計をヘンリー伯父が持っていたら
12時間40分の睡眠ですね、
実はこのような時計は売っています。
コメント
ごめんなさい、ひっかけるつもり(?)でした。
こういう失敗をした経験、ありませんか?
私はあります。
気を利かせたつもりが、夕方頃鳴り出してしまうという・・・。
24時間用の目覚まし時計を売っているという話しですが、
これは便利かもしれませんね。
でも考えてみれば、それが必要なのは12時間以上、
眠りたいときですよね。
今の私の現実にはむずかしいかも。
Hungry Bear
水の流れ
Nagahiro
ネットOL
マサボー
2年4組情報処理科 全員
 戻る
戻る