問題195　４色の正方形

一部修正（3日、23:55）

赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の１辺の長さは赤が１cm、白が２cm、青が４cm、緑が８cmです。いま、赤、白、青、緑の正方形がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を記号（○,△,◇,◎）で表わすことにします。
例えば、赤１枚、白１枚、青１枚、緑１枚のときの総面積は、次のようになります。
（１，１，１，１）＝１×１×１＋２×２×１＋４×４×１＋８×８×１＝８５cm²
また、紙を取りかえる次の操作を行います。

操作：赤４枚は白１枚に、白４枚は青１枚に、青４枚は緑１枚に、それぞれ必ず取りかえる。

次の[　]に適当な数を入れてください。
(1) 操作後の記号が（[ア],[イ],[ウ],[エ]）のとき、総面積は、１７３cm²です。

(2) 操作前の記号が、（[８],[オ],[５],[１]）のとき、操作後の記号は、（[カ],[２],[３],[２]）

問題の出典

大人の算数パズル
河瀬　厚
慶應義塾中等部　2006年
自由国民社

解答

～到着順にご紹介します～

解答・その1

（ペンネ－ム：haya）

答え：
(1)ア = 1 、イ = 3、ウ = 2、エ = 2
(2)オ = 8 、カ = 0

【解き方】
(1) エ64づつ変化し、 0, 1, 2 まで可能で、残りの数値は 173, 109, 45
エ=45 の時、ウは操作後であるから 0～3 まで変化可能であるが残り数値が 45, 29, 13 となるから
実際には 0, 1, 2 しか変化できない。　エ=2 の時、イ=3, ア=1 として解を持つ。
エ=0, 1 ではア, イの値が0～3 の間におさまらないから解を持たない。
エ=109, 173 も同様に解を持たない。

(2) 当然
オ = 8、カ = 0 となる。

解答・その2

（ペンネ－ム：スモークマン）

(1)4進法なので…
173/4=43…1
43/4=10…3
10/4=2…2
(1,3,2,2)

(2)
15(オ)8=21(オ+2)0=21(8+2)0=2320=232(カ)
オ=8
カ=0

じっさいに...
4³*1+4²*5+4*8+8=184
4³*2*4²*3+4*2+0=184

解答・その3

（ペンネ－ム：浜田　明巳）

（１）エクセルのマクロで解いた．
　(ａ，ｂ，ｃ，ｄ)＝１７３として解くと，解は，
　　ア＝１，イ＝３，ウ＝２，エ＝２
の１組である．

Option Explicit
Sub Macro1() '(a,b,c,d)=173
     Cells(1, 1).Value = 0
     Dim a As Integer
     Dim b As Integer
     Dim c As Integer
     Dim d As Integer
     For d = 0 To Int(173 / 8 / 8)
       For c = 0 To Application.Min(Int((173 - d * 8 * 8) / 4 / 4), 3)
         For b = 0 To Application.Min(Int((173 - d * 8 * 8 - c * 4 * 4) / 2 / 2), 3)
           a = 173 - d * 8 * 8 - c * 4 * 4 - b * 2 * 2
           If a < 4 Then
             Cells(1, 1).Value = Cells(1, 1).Value + 1
             Cells(Cells(1, 1).Value, 2).Value = a
             Cells(Cells(1, 1).Value, 3).Value = b
             Cells(Cells(1, 1).Value, 4).Value = c
             Cells(Cells(1, 1).Value, 5).Value = d
           End If
         Next b
       Next c
     Next d
End Sub

（２）
　　(８，オ，５，１)＝(カ，２，３，２)
　　∴(０，オ＋２，５，１)＝(カ，２，３，２)
　　∴(０，オ＋２，１，２)＝(カ，２，３，２)
　　∴カ＝０，オ＋２－４×２＝２
　　∴オ＝８，カ＝０

解答・その4

（ペンネ－ム：のっこん）

アをa,イをb,ウをc,エをd,オをx,カをyとする
(1)
a+4b+16c+64d=173
d=0の時　a+4b+16c=173
d=1の時　a+4b+16c=109
d=2の時　a+4b+16c=45
操作後においてはa≦3,b≦3,c≦3だから
　a+4b+16c≦63 よってa+4b+16c=45 d=2

c=0の時　a+4b=45
c=1の時　a+4b=29
c=2の時　a+4b=13
a+4b≦15だから a+4b=13 c=2

b=0の時　a=13
b=1の時　a=9
b=2の時　a=5
b=3の時　a=1
a≦3だから　a=1 b=3

(2)
操作前の赤8枚は白2枚と交換されて残りはなくなるからy=0
操作の前後において総面積は変わらないから
　1・8+4x+16・5+64・1=4・2+16・3+64・2
4x=32　となりx=8

解答・その5

（ペンネ－ム：マシャ）

(1)

173を4で割り(梯子算), 分解すると 173 = 1*4⁰ + 3*4¹ + 2*4² + 2*4³となるので

答え　(ア,イ,ウ,エ,オ) = (1,3,2,2)

(2)
操作をすることによって, (8,オ,5,1) -> (0(=カ),オ+2-?(=2),1+??(=3),2)となる
ここで, 青の枚数が3になったので, 白から青になった枚数は2
つまり, オ+2から2*4枚取りかえたことになる.
オ+2-2*4=2なのでオは8

答え　オ=8, カ=0

【過程】
問題文を見たときに、2進数かなと思ったのですが、面積だったんで4進数が思いつきました。

解答・その6

（ペンネ－ム：次郎長）

赤の枚数をＡ、白の枚数をＢ、青の枚数をＣ、緑の枚数をＤとします。
赤、白、青4枚は必ず白、青、緑に取り替えるのですから
操作後の枚数は、０＜＝Ａ、Ｂ、Ｃ＜＝３となります。

問題（１）
（ア、イ、ウ、エ）の面積は
（Ａ、Ｂ、Ｃ、Ｄ）＝Ａ＋４Ｂ＋１６Ｃ＋６４Ｄ＝１７３ｃｍ^２
Ａ、Ｂ、Ｃは最大で各３なので、Ａ＋４Ｂ＋１６Ｃの最大は６３。
つまりＤ＝０もしくは１なら不可。またＤ＝３でも成立しない。

結局
Ｄ＝２
この時、Ａ＋４Ｂ＋１６Ｃ＝１７３－６４×２＝４５
Ｃは３以下であるが、Ｃ＝３ではＡ＋４Ｂがマイナスになり、不成立

Ｃ＝２の時、Ａ＋４Ｂ＝４５－１６×２＝１３
Ａ＝０、２，３の時、上記を満たすＢはない。
Ａ＝１の時、Ｂ＝３

Ｃ＝１の時、Ａ＋４Ｂ＝４５－１６×１＝２９
Ａ、Ｂ共に３以下でこれを満たすことはない。
また　Ｃ＝０でも不成立

つまり（Ａ、Ｂ、Ｃ、Ｄ）＝（１、３、２、２）＝（[ア]、[イ]、[ウ]、[エ]）
検算すると、１×１+３×４＋２×１６＋２×６４＝１７３　ＯＫ

問題（２）
（８、オ、５，１）＝（０、オ＋２、５，１）＝（０、オ＋２、１、２）⇒（カ、２、３、２）
カ＝０

真ん中の２つ、
【オ＋２、１】が【２、３】になるということは、オが８なら、【１０，１】⇒【２，３】になる
これでＯＫ
オ＝８

こんなややこしい説明せずに、
８＋オ×４＋５×１６＋１×６４＝カ×１＋２×４＋３×１６＋２×６４
オ×４＝カ＋３２
カは、０，１，２，３のどれかなので、それを満たすのは。オ＝８、カ＝０の時のみ

つまり、
（８、８、５，１）が（０，２，３，２）になったわけですね。

検算、
左辺　８×１＋８×４＋５×１６＋１×６４＝１８４
右辺　０×１＋２×４＋３×１６＋２×６４＝１８４
OKですね
記号がやけにややこしくて、ああしんど。

解答・その7

（ペンネ－ム：転位反応）

設問（１）
余りが割る数よりも小さくなるように、173を64, 16, 4, 1 で順に割る。

　　　173=64×2+45
         =64×2+16×2+13
         =64×2+16×2+4×3+1×1

∴（［ｱ］､［ｲ］､［ｳ］､［ｴ］）=（1,3,2,2）

設問（２）
［ｶ］について、操作前が8であり、8=4×2+1×0　なので、［ｶ］=0である。
また、操作前後で面積が変わらないことから、

　　1×8+4×［ｵ］+16×5+64×１
　　=4×2+16×3+64×2
　　=184

∴ 4×［ｵ］=32
∴ ［ｵ］=8

解答・その8

（ペンネ－ム：まーりんａｎｄさとりん）

（１）
１×ア＋４×イ＋１６×ウ＋６４×エ＝１７３となるためには、エは２枚　以外ない。
１×ア＋４×イ＋１６×ウ＝１７３－１２８＝４５となるためには、ウは２枚　以外ない。
１×ア＋４×イ＝４５－３２＝１３となるためには、アは１枚　イは３枚　となる。

答．ア：１枚　イ：３枚　ウ：２枚　エ：２枚

（２）
操作後が（[カ],[２],[３],[２]）なので
　　１×カ＋２×４＋３×１６＋２×６４＝カ＋１８４　カは０，１，２，３のいずれかなので、
総面積は　１８４，１８５，１８６，１８７のいずれかになる。　

一方、操作前の面積は
　　８＋４×オ＋１６×５＋６４×１＝４×オ＋１５２
と表せる。操作が何回あっても面積の総和は変わらないので、オが整数となるためには
　　４×オ＋１５２＝１８４
しかない。　よってオは８枚　カは０枚

答．オ：８枚　カ：０枚

解答・その9

（ペンネ－ム：紀伊龍洸）

この問題は、２べきの桁上り演算の問題とみなすことができる。
＃４進数。

（１）
総面積の１７３を二進数に変換する。
　　172 (10) ＝ 10 10 11 01 (2) ＝ 2 2 3 1 (4)
（[ア],[イ],[ウ],[エ]）＝　（[1],[3],[2],[2]）

（２）
操作前の記号、（[８],[オ],[５],[１]）　の最小位[８]に注目する。
8 (10) ＝ 2 0 (4) である。
したがって、操作後は桁上がりにより最小位（赤の位置）の数は　０になる。
故に、[カ]　＝　[0]
故に操作後の記号は、（[０],[２],[３],[２]）である。
故に総面積　＝　１×０＋４×２＋１６×３＋６４×２　＝　１８４
操作前の記号による総面積　＝　１×８＋４×[オ]＋１６×５＋６４×１
操作前後で総面積は変わらないから両者の差をとって[オ]を求める。
[オ]　＝　（１８４－８－１６×５－６４×１）／４　＝　３２／４　＝　８
答え：
[ア],[イ],[ウ],[エ],[オ],[カ] ＝ [１],[３],[２],[２],[８],[０]

解答・その10

（ペンネ－ム：オヤジ）

この問題は、４色の正方形といいながら、４進法の問題であり。数字を左右逆に並べる、問題である。
すなわち、各色の面積は，赤：４^０，白：４^１，青：４^２，緑：４^３　である。

（１）
１７３＝４^３×２＋４^２×２＋４^１×３＋４^０×１
従って（１，３，２，２）＝（［ア］，［イ］，［ウ］，［エ］）
∴　［ア］＝１、［イ］＝３、［ウ］＝２、［エ］＝２

（２）
（［８］，［オ］，［５］，［１］） →　（［カ］，［２］，［３］，［２］）
（［８］，［オ］，［５］，［１］）＝（［０］，［オ＋２］，［１］，［２］）＝（［０］，［オ－６］，［３］，［２］）＝（［カ］，［２］，［３］，［２］）　
従って　［オ］＝６＋２＝８，［カ］＝０
∴　［オ］＝８、［カ］＝０

解答・その11

（ペンネ－ム：ちょろんは太太）

色紙の枚数は、４進法に対応し、１の位は赤、４の位は白、１６の位は青、６４の位は緑の枚数で、表されている。紙の取替え作業は、位上げに対応して、それぞれの位の数が０～３になるようにする作業である。

（１）　173の４進法を考える。
　　　　173÷4=43…1
　　　　43÷4=10…3
　　　　10÷4=2…2
173 の4進法表記は、2231
答え　　[ア]　：　1 、 [イ]　：　3 、 [ウ]　：　2 、 [エ]　：　2

（２）　赤紙８枚は操作後は、白２枚におきかえられるので、 [カ]　：　0
　　　　操作前の面積は、1 x 8 + 4 x [オ] + 16 x 5 + 64 x 1
　　　　操作後の面積は、0 x 8 + 4 x 2 + 16 x 3 + 64 x 2
これを等しいとして解くと、　[オ]　：　8
答え　　[オ]　：　8 、 [カ]　：　0

解答・その12

（ペンネ－ム：杖のおじさん）

答えは
（１）　ア＝１　　　イ＝３　　　ウ＝２　　エ＝２
（２）　ア＝８　　　イ＝０　　です。
左側から赤１cm²、白２cm²、青４^cm2、緑８cm²の順番に色紙があります。
（１）の解答
ア＋イ＋ウ＋エ＝１７３cm² 各色一枚の（１、１、１、１）の時は１＋４＋１６＋６４＝８５cm²なので各色二枚とすると１７０cm²となり3cm²分少ない。
従って、２，２，２，２に３cm²分の３、０，０，０を加算すると５、２，２，２となります。
これを整理して１，３，２，２となります。
答えは　ア＝１　イ＝３　ウ＝２　エ＝２　です。

（２）の解答
　８、オ、５、１　→　カ、２、３、２となるには
オが８であれば８、８、５、１　
一回目操作　０、１０、５、１
二回目操作　０、２、７、１
三回目操作　０、２、３、２となります。

また左の桁から考えてもみました。
８、オ、５、１
一回目操作　カ、２、１，２
下二桁目を３にするにはオは８でなければならない。
従って８、８、１、２となり
二回目操作　８、０、３、２となり
三回目操作で　０、２、３、２となります。
面積は１８４cm²となります。答えはオ＝８、カ＝０です。

解答・その13

（ペンネ－ム：T_Tatekawa）

(1) 赤，白，青，緑の正方形の面積はそれぞれ 1, 4, 16, 64cm²．
総面積を面積の大きい順に正方形で分けていく事を考える．

　　173÷64 = 2 あまり 45
　　45÷16 = 2 あまり 13
　　13÷4 = 3 あまり 1
よって (1, 3, 2, 2)
ア=1, イ=3, ウ=2，エ=2．

(2) まず数字が明らかなところから取り替え操作を行うと，
　　（[8],[オ],[5],[1]）→（[0], [オ+2], [1], [2]）
となる．操作後は
　　（[カ],[2],[3],[2]）
なので，カ=0．
次に，操作後は青い正方形が2枚増えている事になるので，
　　オ+2 - 2×4 = 2
ということになる．よってオ=8

解答・その14

（ペンネ－ム：夜ふかしのつらいおじさん）

（１）もし、操作のルールが
「赤４枚を白１枚に、白４枚を青１枚に、青４枚を緑１枚に、それぞれ取りかえる。」
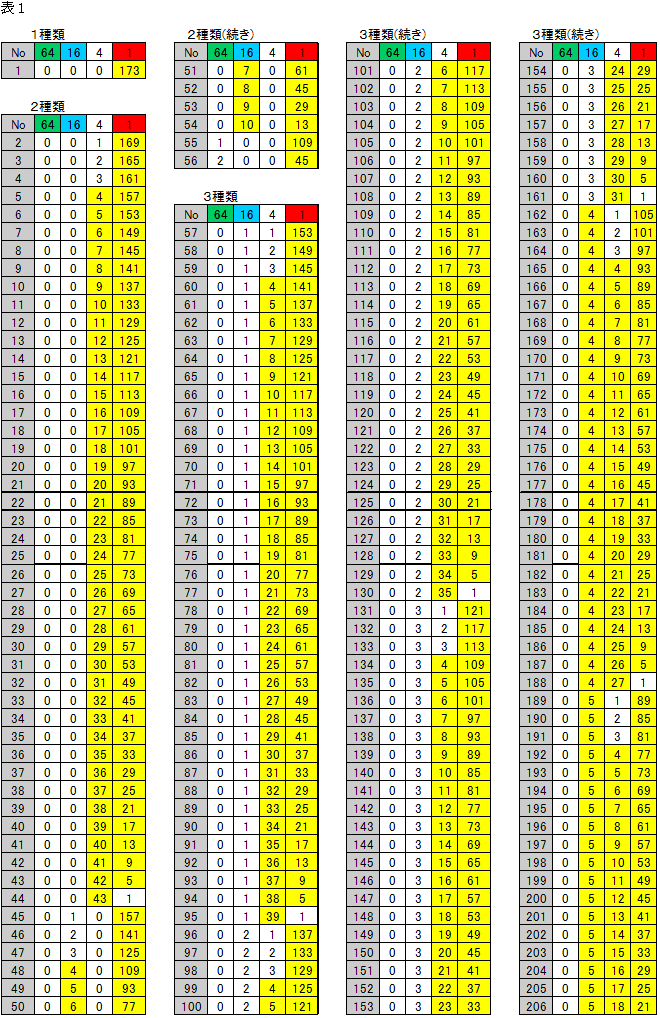
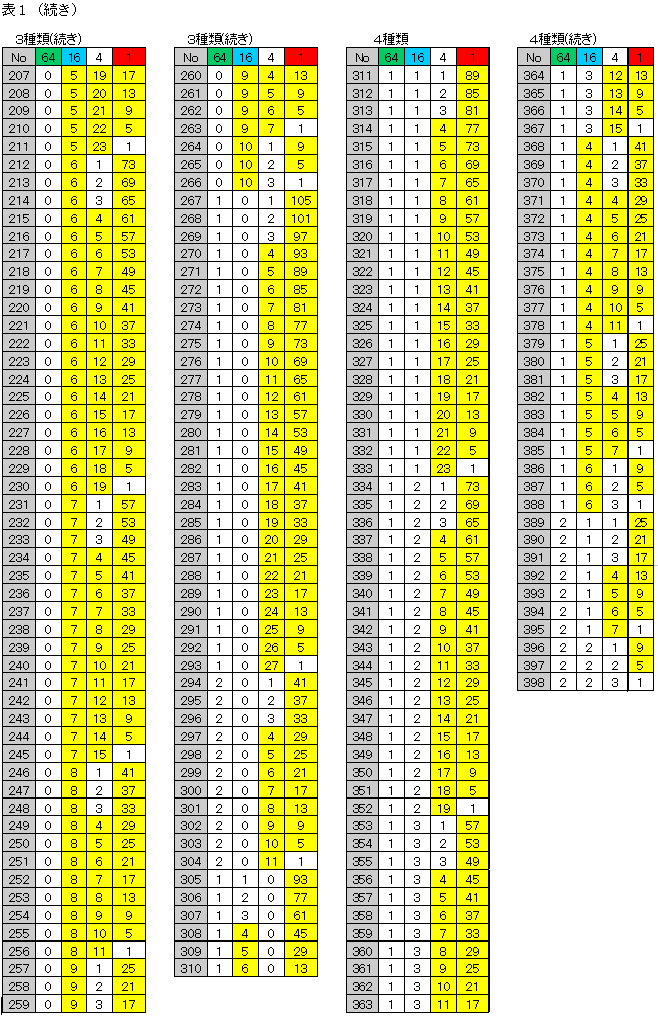
だとすると、操作に特に制限がないので、次の表１のNo1以外が答えになりえます。
始め赤が１７３枚あったとすると、赤４枚を白１枚に取りかえれば、No1からNo2の状態になります。

しかし、操作のルールが
「赤４枚は白１枚に、白４枚は青１枚に、青４枚は緑１枚に、それぞれ必ず取りかえる。」
なので、表のNo398が答えになります。
４枚以上のものは、必ず取りかえるので青以外は必ず３枚以下になります。（表の黄色い部分は４枚以上）
この問題は、１７３を４進法で表すことと同じなので、次のような方法で答えが求まります。

１７３を４進法で表すと、
　１７３（１０）＝２２３１（４）
となります。
なお、３×４³＋３×４²＋３×４＋３＝２５５なので２５６以上の場合、緑の枚数が４を超えます。

（２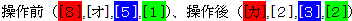）　　となっています。
操作前赤が[８]（４×２）なので、カ＝０です。
白のオに２を加えたものが[２]となっているので、オは、[４×ｎ]の形の数です。
緑が[１]から[２]と１枚増えているので、青は４枚だけ緑に取かえられました。
青が[５]から[３]となっているので、白から青に２枚が加えられました。
よってｎ＝２なので、オ＝８です。

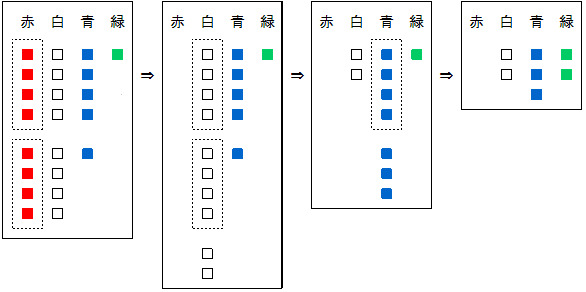
解答・その15

（ペンネ－ム：Ryuto）

（１）
赤 1×1=1
白 2×2=4
青 4×4=16
緑 8×8=64 これが一枚の面積

173-64×2=45
45-16×2=13
13÷4=3・・・1
→　赤1 白3 青2 緑2となる

（２）
8・x・5・1=y・2・3・2

x=4×2
x=8
y=0
結果
8・8・5・1=0・2・3・2となる

解答・その16

（ペンネ－ム：迷子の雄猫）

（１）
正方形の１辺の長さは赤が１cm、白が２cm、青が４cm、緑が８cmです。
正方形の面積は赤が1cm²、白が4cm²、青が16cm²、緑が64cm²です。
よって173=64+64+16+16+4+4+4+1より
操作後の記号が（[1],[3],[2],[2]）のとき、総面積は、173cm²です。

（２）
（[8 ],[8 ],[5 ],[1 ]）
（[8-8],[8+2 ],[5 ],[1 ]）
（[0 ],[10 ],[5 ],[1 ]）
（[0 ],[10-8],[5+2],[1 ]）
（[0 ],[2 ],[7 ],[1 ]）
（[0 ],[2 ],[7-4],[1+1]）
（[0 ],[2 ],[3 ],[2 ]）

よって操作前の記号が、（[8],[8],[5],[1]）のとき、
操作後の記号は、（[0],[2],[3],[2]）になります。
よって（ア,イ,ウ,エ,オ,カ）＝（1,3,2,2,8,0）

解答・その17

（ペンネ－ム：浦岡）

（１）この問題では闇雲に候補を絞り込むよりも，操作後のア～エがそれぞれ０～３のいずれかであることと，４の倍数に目をつけて式を整理すると首尾良く値を求めることができます。
（ア，イ，ウ，エ）＝１７３より，
ア＋４×イ＋１６×ウ＋６４×エ＝１７３
４×イ＋１６×ウ＋６４×エ＝１７３－ア＝（４の倍数）　→ア＝１に決まります。
４×イ＋１６×ウ＋６４×エ＝１７２
イ＋４×ウ＋１６×エ＝４３
４×ウ＋１６×エ＝４３－イ＝（４の倍数）　→イ＝３に決まります。
４×ウ＋１６×エ＝４０
ウ＋４×エ＝１０
４×エ＝１０－ウ＝（４の倍数）　→ウ＝２に決まります。
４×エ＝８
エ＝２
【答】ア＝１，イ＝３，ウ＝２，エ＝２

（２）まず，ア＝８より，カ＝０に決まります。あとは一本道でオが求まります。
操作の前後で総面積は変わらないので，
（８，オ，５，１）＝（０，２，３，２）
８＋４×オ＋１６×５＋６４×１＝４×２＋１６×３＋６４×２
４×オ＝３２
オ＝８
【答】オ＝８，カ＝０

解答・その18

（ペンネ－ム：三角定規）

(1) 173＝1×1＋4×3＋4²×2＋4³×2＝(1，3，2，2)　…[答]

(2) (8，x，5，1)＝8＋4x＋16×5＋64×1＝4x＋152
　　(y，2，3，2)＝y＋4×2＋16×3＋64×2＝y＋184
　∴ 4x＋152＝y＋184
　∴ 4x－y＝32
　0≦y≦3 より y＝0，x＝8　　よって， (8，8，5，1)＝(0，2，3，2) …[答]

赤、白、青、緑の正方形の紙の面積が、それぞれ、１、４、４^２、４^３であることから、４進法で考えればいいことがわかります。ただし、夜ふかしのつらいおじさんの解答にあるように、「必ず取りかえる」という条件が不可欠ですね。

長い間、「Weekend　Mathematics」をお読みいただいた方々、ご参加いただいた方々に深く感謝いたします。 195回、16年にわたり、続けてこられたのも、皆さんのおかげです。本当にどうもありがとうございました。しばらく、お休みをいただくことにしました。何らかの形で再開する際には、是非またよろしくお願いいたします。

Challenge!