問題194 2種類の硬貨
ある国には、6円玉と7円玉の2種類しかお金がありません。
問1
この国では、おつりをもらわなければ絶対に支払うことができない値段が、全部で何種類ありますか。
問2
そのうちで、もっとも高い値段はいくらですか。
問題の出典
第2回算数オリンピック 予選
パズル気分で算数オリンピック
東大算数研究会・編集
講談社
解答
〜到着順にご紹介します〜
解答・その1
(ペンネ−ム:浜田 明巳)
エクセルのマクロで解いた.
1,2,3,4,5,8,9,10,11,15,16,17,22,23,29の15種類で,
最も高い値段は29円である.
Option Explicit
Const max As Long = 100000
Sub Macro1()
Sheets("Sheet1").Select
Dim a(max) As Integer
Dim b As Long
Dim j As Long
Dim jj As Long
For j = 1 To max
a(j) = 0
Next j
For j = 0 To Int(max / 10)
For jj = 0 To Int(max / 10)
b = 6 * j + 7 * jj
If 0 < b And b <= max Then
a(b) = 1
End If
Next jj
Next j
Cells(1, 1).Value = 0
Range("A1").Select
For j = 1 To max
If a(j) = 0 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = j
End If
Next j
End Sub
(別解)
6x+7y(x,yは非負整数)で表すことのできる,またはできない数を考える.
6=6・1+7・0 7=6・0+7・1 12=6・2+7・0 13=6・1+7・1 14=6・0+7・2 18=6・3+7・0 19=6・2+7・1 20=6・1+7・2 21=6・0+7・3 24=6・4+7・0 25=6・3+7・1 26=6・2+7・2 27=6・1+7・3 28=6・0+7・4
であり,1,2,3,4,5,8,9,10,11,15,16,17,22,23,29の
15個の数は表し得ない.
次に30以上の数はすべて表すことができることを示す.
nを5以上の整数とし,6x+7yを6で割った余りで分類する.
i).6x+7y=6nのとき,(x,y)=(n,0)とすればよい.
ii).6x+7y=6n+1のとき,
6(x−n)+7y=1
上記のことから,x−n<0となる.
x−n=−1とすると,
7y=1+6 ∴y=1
故に(x,n)=(4,5),(5,6),(6,7),・・・とすればよい.
故に5以上のすべてのnについて,x,yが存在する.
iii).6x+7y=6n+2のとき,
6(x−n)+7y=2
x−n=−2とすると,
7y=2+12 ∴y=2
故に(x,n)=(3,5),(4,6),(5,7),・・・とすればよい.
iv).6x+7y=6n+3のとき,
6(x−n)+7y=3< BR> x−n=−3とすると,
7y=3+18 ∴y=3
故に(x,n)=(2,5),(3,6),(4,7),・・・とすればよい.
v).6x+7y=6n+4のとき,
6(x−n)+7y=4
x−n=−4とすると,
7y=4+24 ∴y=4
故に(x,n)=(1,5),(2,6),(3,7),・・・とすればよい.
vi).6x+7y=6n+5のとき,
6(x−n)+7y=5
x−n=−5とすると,
7y=5+30 ∴y=5
故に(x,n)=(0,5),(1,6),(2,7),・・・とすればよい.
以上より,6x+7yは30以上のすべての整数を表し得る.
(1)の答は,15種類
(2)の答は,29円 である.
解答・その2
(ペンネ−ム:haya)
答え:
(1) 15種類 (2) 29
【解き方】
6より小さい数は表せないから、1, 2, 3, 4, 5 は当然。
その上を探ると、8, 9, 10, 11, 15, 16, 17, 22, 23, 29 で、それ以上はない。

解答・その3
(ペンネ−ム:T_Tatekawa)
まず 6 円玉を何枚か持っていて,7 円玉に置き換えていく事を考えます.
支払いたい金額を 6 で割って余りが 1 の場合は,6円玉 を 7円玉に
1枚入れ替えられればピッタリ支払う事が出来ます.
同様に,余りがある数の場合,その枚数だけ6円玉 を 7円玉に
入れ替えられればピッタリ支払う事が出来ます.
この考え方によって種類を数え上げると,
6円玉を1枚も持っていない場合は 5 種類はおつりが出ます.
1枚だけの場合は 4 種類.
同様に考えて
5+4+3+2+1 = 15 種類
2) 6で割った余りの最大は 5 なので,
6 x 4 + 5 = 29円
解答・その4
(ペンネ−ム:紀伊龍洸)
問1が、5+4+3+2+1=15で15種類、
問2が、15+2+3+4+5=29で29円ですか。
解答・その5
(ペンネ−ム:スモークマン)
6a+7b
=6a+(6+1)b
=6(a+b)+b…a≧1
払える額…
b=0…6a…6以上の6n
b=1…6(a+1)+1…7以上の6n+1
b=2…6(a+2)+2…14以上の6n+2
b=3…6(a+3)+3…21以上の6n+3
b=4…6(a+4)+4...28以上の6n+4
b=5…6(a+5)+5…35以上の6n+5
つまり…
(1) 払えない額は…
35未満の6n+5…5,11,17,23,29
28未満の6n+4…4,10,16,22
21未満の6n+3…3,9,15
14未満の6n+2…2,8
7未満の6n+1…1
の15種類
(2)?そのうちで、もっとも高い値段は29円
解答・その6
(ペンネ−ム:まーりんandさとりん)
問1
5+4+3+2+1=15 15通り
問2
29円
(理由)
支払額は、6n+k (kは0,1,2,3,4,5のいずれか)と表せる。
6n+k=6(n-k)+7k
なので、 nが5以上ならば、必ず0以上の整数(n−k)が存在する。
よって6×5=30以上の整数はすべて6と7の和で表すことができる。
解答・その7
(ペンネ−ム:夜ふかしのつらいおじさん)
●おつりがなくても支払うことのできる値段を調べます。
○k円が支払可能ならば、k+6n円やk+7n円も支払が可能です。
6と7の最小公倍数42までを調べれば十分です。
値段をカレンダーのように表に整理すると考えやすくなります。
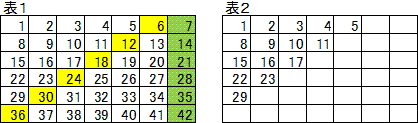
表1のように、6の倍数は斜めに、7の倍数は縦に現れます。
この値段はおつりなしで支払が可能です。
○次に、表1の6と7の倍数に囲まれた数{13,19,20,25,・・・}について考えます。
これらの数は、黄色の数の下、または緑の数の斜めにあります。
これらの数は、上にある黄色の数と7nの和、または斜めにある緑の数と6nの和になります。
つまりこれらの値段はおつりなしで支払が可能です。
●残った表2の値段は、おつりなしでは支払うことができません。
問1 おつりをもらわなければ絶対に支払うことができない値段は全部で15種類です。
問2 もっとも高い値段は29円です。
解答・その8
(ペンネ−ム:のっこん)
[1]1から43までをカレンダーに似せて次のように書く
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| 43 |
[2]6の倍数・7の倍数に○をつける
6、12、18、・・・、7、14、21、・・・に○がつく
[3]nを1以上の整数として(以下同じ)、(6+7n)の数に○をつける
13、20、27、・・・に○がつく
[4](12+7n)、(18+7n)、(24+7n)、(30+7n)、(36+7n)の数に○をつける
19、26、・・・、25、32、・・・、31、38、・・・、37、・・・、43、・・・に○がつく
[5](7+6n)の数に○をつける
13、19、25、・・・と斜めに○がついていくが、それらにはもう○がついている
[6](14+6n)、(21+6n)、(28+6n)、(35+6n)の数に○をつける
斜めに○がついていくが、それらにはもう○がついている
○がついていないのは 5+4+3+2+1=15(個)
最大は29
解答・その9
(ペンネ−ム:転位反応)
N円の商品を6円硬貨n枚、及び7円硬貨m枚でお釣りを貰うことなく支払ったとすると、
N=6n+7m (n,m≧0、整数)
そこで、n,mに具体的に数値を入れてNの値を書き出してみると下表の通りになる。
なお、m=6の場合、6円硬貨の枚数として数えるので、m≦5 の範囲で良い。
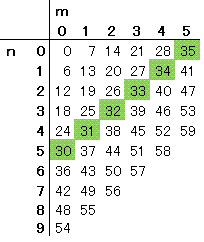
さて、例えば、n=30〜35に注目してNの並び方をみると、
N⇒N+1では、n⇒n−1、m⇒m+1の規則性があることが解る。
そして、この関係は、N=6n+7mを変形して導くことができる。
N=6n+7m
=6(n−1)+6+7(m+1)−7
=6(n−1)+7(m+1)−1
∴N+1=6(n−1)+7(m+1)
∴N≧30の商品はすべて、6円と7円の硬貨でお釣りを必要とすることなく支払いできる。
∴求めるNは、上記の表に出てこない数値である。
列記すると、1,2,3,4,5,8,9,10,11,15,16,17,22,23,29の15種類
最も高い値段は29
解答・その10
(ペンネ−ム:次郎長)
答え
問1) 15種類
問2) 29円
1.6円と7円は、どちらかの硬貨1枚で支払える
1A)6円未満の1-5円の 【5種類】 はおつりが必要なことは自明です
2.硬貨2枚ずつの12-14円は、6円2枚、6円7円各1枚、7円2枚で支払える
2A) その間の、8,9,10,11円の 【4種類】 はおつりが必要ですね。
3.硬貨3枚ずつの18-21円は、6円3枚、6円2枚7円1枚、6円1枚7円2枚、7円3枚で支払える
3A) その間の、15,16,17円の 【3種類】 はおつりが必要
4)同様に、硬貨4枚ずつの24-28円は、6円4枚、6円3枚7円1枚、6円2枚7円2枚、6円1枚7円3枚、7円4枚で支払える
3A) 同様にその間の、22,23円の 【2種類】 はおつりが必要
4)同様に、硬貨5枚ずつの30-35円は、6円5枚、6円4枚7円1枚、6円3枚7円2枚、6円2枚7円3枚、6円1枚7円4枚、7円5枚で支払える
3A) つまり、29円の【1種類】はどうしてもおつりが必要
以上から、おつりが必要なのは、1,2,3,4,5円と8,9,10,11円と15,16,17円と22,23円と29円の 【15種類】
もっとも高い値段は29円となります。
36円より高い値段は30円から35円までの連続した6つの値段が支払えることが分かったので、
6円ずつ足していけばずっとOKですね。
解答・その11
(ペンネ−ム:ちょろんは太太)
6円玉 m個、7円玉n個で支払うとする。ただし、m≧0 n≧0
支払える金額は、6m + 7n = 6(m + n) + n
6で割った余りを n とすると、その商が、n より少ない場合はその金額にすることはできない。
余り 1 で、商 0 の場合
余り 2 で、商 0、1 の場合
余り 3 で、商 0 、1、2 の場合
余り 4 で、商 0 、1、2、3 の場合
余り 5 で、商 0 、1、2、3、4 の場合
従って、15通りは、その金額にすることはできない。
また、最も大きな金額は、商が4で余りが5の場合、即ち、29
問1の答え 15種類
問2の答え 29
解答・その12
(ペンネ−ム:浦岡)

解答・その13
(ペンネ−ム:オヤジ)

従って 赤い色の数が、おつりをもらわなければ支払うことが困難な金額
Q1 ∴ 15種類
Q2 ∴ 29円 (上記表より)
解答・その14
(ペンネ−ム:迷子の雄猫)
6円5枚で30円を支払うことができる。
6円を7円に変えると1円増えるので、30円から35円までは支払うことができる。
30円から35円までにそれぞれ6円を加えると36円から42円までは支払うことができる。
以下同様に考えて43円以上なら支払うことができる。
よって30円未満がおつりなしで払えるか考える。
6円何枚かに、30円以上になるまで7円を加えていくことにする。
0,7,14,21,28,35
6,13,20,27,34
12,19,26,33
18,25,32
24,31
30,
よっておつりなしに支払えないのは
1,2,3,4,5,8,9,10,11,15,16,17,22,23,29の15通り
さて、こういう問題を出されると一般化する人が必ずいるはず。
ということで調べてみると、こんな記述がありました。
「互いに素な自然数m円,n円の硬貨があれば、
(m-1) (n-1) 円以上なら支払う方法があることは簡単に証明できる。」
証明が書いてなかった(汗)ということでチャレンジしてみることに。
m<nとする。m,nは互いに素とする。
0,n,2n,3n, ... , (m-1)n をそれぞれmで割った余りを考える。
数がm個あるので、余りも0から(m-1)まで重複無く出てくるはずである。
もし0,n,2n,3n, ... , (m-2)n, (m-1)n をそれぞれmで割った余りが重複したとする。
重複した2数をpn,qn(ただしp<q<m)とする。そうすると(q-p)nはmで割り切れるので、
(q-p)=jとおいてjn=kmと書ける。
n,mは共通の素因数を持たないので、j=rm かつ k=rn (rは自然数)でないとこの式が成立しない。
j=(q-p)<mであるのにj≧mであるのは矛盾する。
よって余りも0から(m-1)まで重複無く出てくる。
さて、(m-1)n-(m-1),(m-1)n-(m-2), ... ,(m-1)n-1, (m-1)n-0 をそれぞれmで割った余りを考える。
(m-1)n-(m-1)つまり(m-1)(n-1)から(m-1)nまでの連続するm個の自然数であるので、
余りも0から(m-1)まで重複無く出てくるはずである。
よって集合A{0,n,2n,3n, ... , (m-2)n }と集合B{(m-1)n-(m-1),(m-1)n-(m-2),... ,(m-1)n-1}を考えると、
集合Aの要素と集合Bの要素を、mで割った余りが同じ数同士で1対1に組みあわせることができ、
かつ集合Bの最 小の要素(m-1)n-(m-1)は集合Aの最大の要素(m-2)n=(m-1)n-nよりも大きいので、
集合Aの要素にmの整数倍を適宜加えた 集合A'{0+a1m,n+a2m,2n+a3m,3n+a4m, ... }が
集合Bと同じになるように出来る。
よって、(m-1) (n-1)から(m-1)nまでの連続するm個の自然数を
am+bn ( a≧0,b≧0 )
という形式で表すこと ができるので、(m-1) (n-1)以上の自然数を
am+bn ( a≧0,b≧0 )
という形式で表すことができる。
m=3,n=4のとき(m-1) (n-1)-1は5になるが、5は3a+4b ( a≧0,b≧0 )という形式で表
すことができない ので、(m-1)(n-1)-1以下の数はam+bn ( a≧0,b≧0 )という形式
で表すことができるとは限らない。
証明終わり
解答・その15
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
答え
[1]15種類です。 [2]29です。
次のように表1又は表2を作って考えました。
表を作るに当っては各段の数列の項差が6円+7円=13円等でも良いと思います。
表1 7円の項差の表
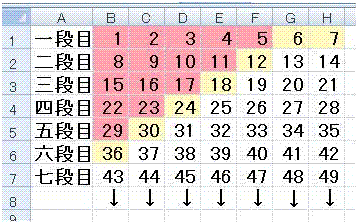
表2 6円の項差の表
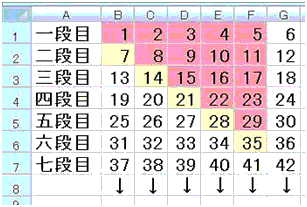
表1は1から7までの数字に7を加算した数字が並んでいます。
表2は1から6までの数字に6を加算した数字が並んでいます。
ピンクの部分以外の場所にある数字は全部6円玉と7円玉で支払えます。
例えば、40円は6円玉2枚と7円玉4枚となります。
150円はどのようになるか計算してみます。
7円玉で支払う方法は7で割って残りが6の倍数になるまで検算します。
150÷7=21枚残り3円
20枚だと残り10円
19枚だと残り17円
18枚だと残り24円、ここで6円の倍数になります。
従って、150円の支払いは7円玉18枚、6円玉4枚で支払います。
6円玉で支払う方法は6で割って残りが7の倍数になるまで検算します。
150÷6=15枚
ピンクの部分は6円又は7円で割った残りが6円、7円玉で支払えませんので
答えは
[1] 1円、2円 3円、4円、5円、8円、9円、10円、11円、
15円、16円、17円、22円、23円、29円、の15種類です。
[2] 29円です。
解答・その16
(ペンネ−ム:Asterisk*)
問1
おつりをもらわなければ支払えない値段は、全部で15種類あります。
1,2,3,4,5,8,9,10,11,15,16,17,22,23,29円
問2
そのうちで、もっとも高い値段は29円です。
まず、6円と7円で支払うことの出来る金額を計算します・・
しかし、6+6, 6+7, 7+7...と計算するのは難しいので
6と7から始まる足し算の表を作りました。
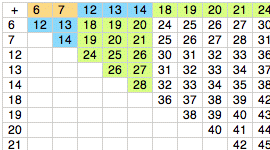
解答・その17
(ペンネ−ム:SOU)
☆前置き
値段,6円玉の枚数,7円玉の枚数を各々z,x,y とすると、
z = 6x + 7y ( x,y ∈ Z , z ∈ N)
のように表すことができる。
☆この式からわかること
[1]x を1つ減らし、y を1つ増やすとz は1増える。逆なら1減る。
[2]x,y のどちらかが負になるということは、お釣りが発生するということ。
☆問2を考える
6の倍数を、6による商をp として
z = 6p
と表す。(z が正ならp も正)
この数から1づつ増やした5つの値 z+1 , z+2 , ・・・ , z+5 を作ることを考える。
[1]を利用すると、
z+1 = 6*(p-1) + 7*1
z+2 = 6*(p-2) + 7*2
・・・
z+5 = 6*(p-5) + 7*5
のように表現できる。
ここで[2]から、() 内は負にしてはならない。
即ち、p≧5 でなければ安全と言えない。
(逆に p=5 即ち z=30 以上の全ての値段に対しては、正の2数 x,y の組みが存在することがわかった。)
さしあたってp=4 の時を考えると、連続した5数は
24,25,26,27,28,29
であるが、題意から大きい方を先に調べる。
29 について考えると、その値を満たす正の2数 x,y の組みは存在しないのでこれが答え。
☆問1を考える
以上のことから29以下の値に対してお釣りなしで支払えるものを調べると
6,7,12,13,14,18,19,20,21,24,25,26,27,28
の14個なので、お釣りなしで支払えないのは15個となる。
解答・その18
(ペンネ−ム:K高校のT・I)
賢いやり方が思い浮かばなかったので「6」と「7」を組み合わせた数を作り、
倍数を書き出してにらめっこ
6,7,13,19,20,25,27,32,33,39,45,46の倍数
6,12,18,24,30,36,42
7,14,21,28,35,42,49
13,26,39,52,65,78
19,38,57,76,95,114
・・・
と並べて抜けている数を小さい方から書き出していくと
1,2,3,4,5,8,9,10,11,15,16,17,22,23,29,31,34,37・・・となりました
途中までは「1,2,3,4,5」「8,9,10,11」「15,16,17」「22,23」「29」というように
連続する数がだんだん少なくなっていく規則性なのではないかと予想したのですが
31,34,37と数字が出てきた結果一時混乱。
その後「29」以降の数はすべて「6」と「7」で表すことができることに気づき解決
答えは
問1 15種類
問2 29円
となりました
解答・その19
(ペンネ−ム:三角定規)
6円x枚と7円y枚で支払える金額 N 円は,
6x+7y=N ・・・[1]
[1] の整数解 x,yは,mを整数として
x=7m−N,y=−6m+N
x≧0,y≧0より,6m≦N≦7m ・・・[2]
[1] は,
m=1 のとき,N=6,7
m=2 のとき,N=12,13,14
m=3 のとき,N=18,19,20,21
m=4 のとき,N=24,25,26,27,28
m≧5 のとき,N≧30 のすべての自然数
を表すから,[1]が表すことができないNは,
N=1,2,3,4,5,8,9,10,11,15,16,17,22,23,29
の15種類で,最大の金額は29円。
解答・その20
(ペンネ−ム:Tiki)
(1) 15種類
(2) 29円
おつりをもらわないと払えない金額には、規則性がありますね。
7種類を周期として考えれば、最初は、1〜5円の5種類、次が8〜11円の4種類、
その次が15〜17円の3種類・・・というふうに、払えない金額の幅が1つずつ少
なくなります。
というわけで、払えない金額の総数は、
5+4+3+2+1=15種類、
払えない最大の金額は、
6×5−1=29円
コメント
一般に、互いに素(最大公約数が1)な整数a、bに対して、(a−1)(b−1)以上の整数は、
am+bn(ただし、m、nは自然数)と表すことができます。
迷子の雄猫さんが証明してくださいました。
今回の場合、6と7は互いに素ですから、5×6=30以上の整数は、
6m+7n(ただし、m、nは自然数)と表すことができますので、29以下の整数について、
調べればよいことになります。
 top
top