問題193 帽子をかぶっている人
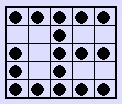
図のようなマス目があって、1マスにつき1人の人がいます。
その人たちの中には、帽子をかぶっている人が何人かいます。
どの人も、たて、よこ、ななめのとなりあったマスにいる人の頭しか見えません。
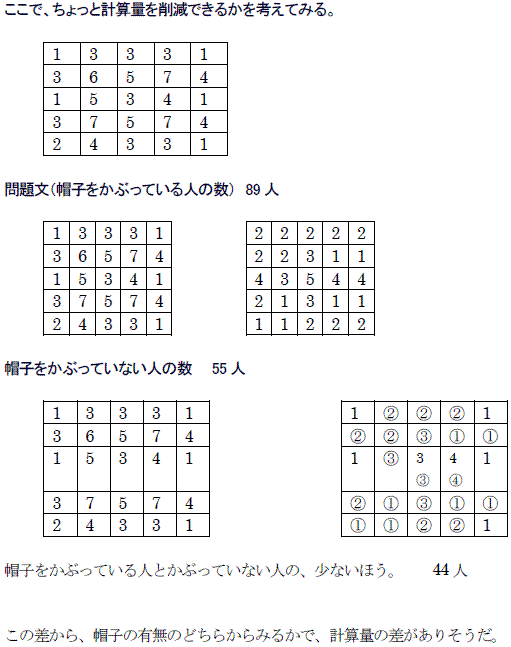
たとえば、図1のAのマスにいる人には、8人の頭が見え、Bにいる人には5人の頭が、
Cにいる人には3人の頭が見えます。自分の頭は見えません。

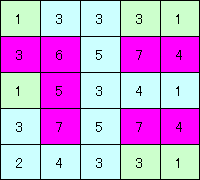
図2のマスの中には、それぞれのマスにいる人から見える、帽子の数が書いてあります。
図2のマスの中で、帽子をかぶっている人がいるマスをすべて黒くぬってください。
そこに表れた文字を答えてください。
問題の出典
第5回算数オリンピック 予選
パズル気分で算数オリンピック
東大算数研究会・編集
講談社
解答
~到着順にご紹介します~
解答・その1
(ペンネ-ム:haya)
答え:
解答・その2
(ペンネ-ム:Ryu1128)
お正月らしく「正」ですね!
1と7からつぶしていけば試行錯誤でもすぐに正解にたどり着きます
解答・その3
(ペンネ-ム:次郎長)
今回の問題は右半分が上下に対象でしたので、
そちらから押さえて、左半分は下に重きがあるようなので、
試行錯誤する積りでしたが、なんと一発で正解。
こいつは正月から縁起がいいわい。
今年もよろしくお願いします
ああ、答えは「正」の字です。
解答・その4
(ペンネ-ム:スモークマン)
お正月らしい問題でしたね☆
「正」の字が浮き出てきました♪

左下四分の1から手をつけました...+試行錯誤...^^;...
解答・その5
(ペンネ-ム:ちょろんは太太)
1と7のマスが、下の左図のような位置関係だと、右のように、○の位置の人は、 帽子をかぶり、×の人は、かぶっていない、△の位置は、どちらかが帽子を かぶっていることが、わかる。
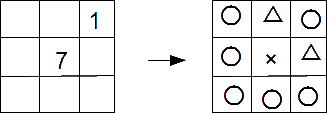
問題のこれより、図中の1と7のマスに注目すると、以下のようになっていることがわかる。
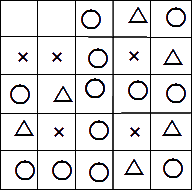
次に、ほかのマスの数字を考えて、順次、各マスの帽子をかぶっているか否かを判断していくと、 以下の答えになる。

答えは、”正”しい
解答・その6
(ペンネ-ム:マシャ)
【解答】
左上を(1,1)とし、各マスを行列表記します.
そして, 注目するマスに従って、帽子の有無を順番に調べます。
1 (5,5)の1からみて(4,4)の7に注目すると
(4,4)の7が帽子を被ると(5,4), (4,5)の2人が被らないことになり
(4,4)の7に矛盾する。なので、(4,4)の7はかぶらない
2 (4,5)の4に注目すると残りの隣り合うマス全てが被ることになる
3 (1,5)の1から(2,4)の7が被らない
4 (2,5)の4の周り全て被る
5 (3,1)の1と(4,2)の7の関係で(4,2)の7が被らない
6 (5,1)の2から周りが被る
7 (5,3)の3から周りが被る
8 (5,2)の4から周りが被る
9 (3,1)の1から周りが被らない
10 (1,1)の1から(1,2)が被る
11 (2,2)の6から周りが被る
12 (5,5)の1から(4,5)が被らない
13 (1,5)の1から(2,5)が被らない
以上から全てのマスの帽子の有無が確定する。
答え 「正」
【過程】
問題文を見たときに、マインスイーパーが彷彿されました。
ですので、順番に小さい数字や大きい数字に注目して、回答が導かれました。
解答・その7
(ペンネ-ム:やなせ)
答えは
正
の文字です。
問題の右1列目の数字の並び
そして2列目の数字と3列目の数字の並び
これを見て感で右側から解いてみたら出来てしまった。
マインスィ-パ-の特訓のお陰かな?
解答・その8
 (ペンネ-ム:杖のおじさん)
(ペンネ-ム:杖のおじさん)
答え 正
右下が①なので⑦の人は帽子をかぶっていない事が確定します。
⑦の人は7人帽子をかぶっている人が見えるので①と④か③のどちらか1人がかぶっている事が確定します。
④がかぶっていると④の人は3人しか見えないので③の人がかぶっている事が確定します。
この様に一マス毎に検証して下の図のようになりました。

解答・その9
(ペンネ-ム:転位反応)
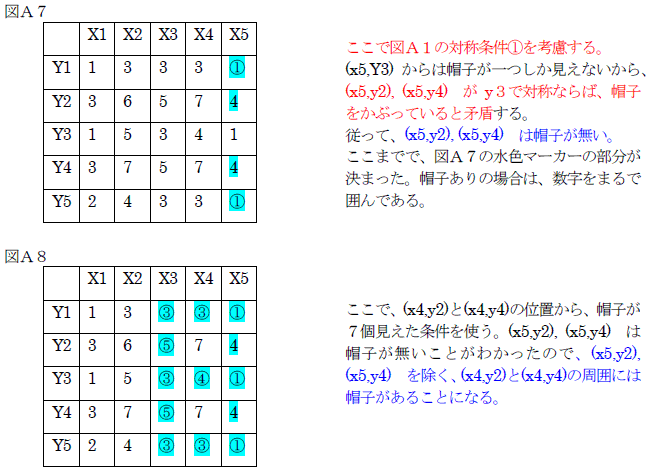
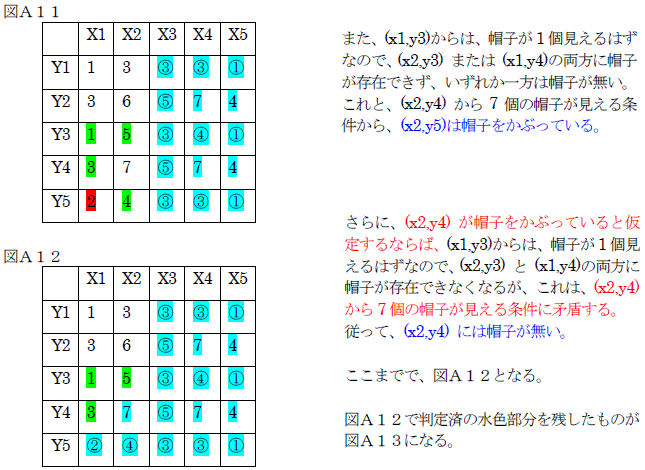
先ず、最も右側の列の数字に着目し、三行目を基準に上下の数字が対象であることから、 黒いマスは以下のように特定できる。

次に、今度は右側から2列目の数字に着目して対象性も考慮すると、黒いマスは以下のように特定できる。

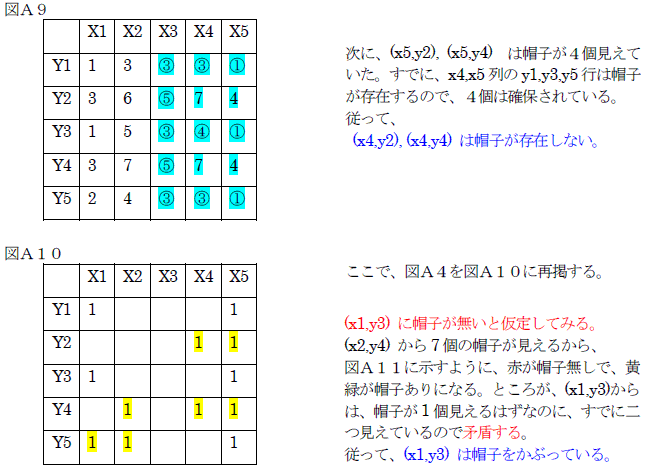
同様に、右側から3列目の数字に着目、対象性も考慮して、黒いマスは以下のように特定できる。

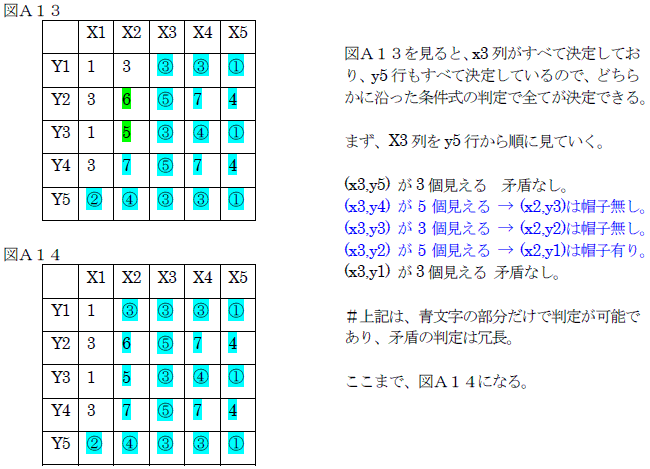
同様に、右側から4列目の数字に着目して、黒いマスは以下のように特定できる。

最後に、最も左の列の数字で正しいことを検証。よって、表れた文字は「正」である。

解答・その10
(ペンネ-ム:まーりんandさとりん)
「正」
解答・その11
(ペンネ-ム:迷子の雄猫)
答え:正。疋だと答えるのは捻くれているだろう、さすがに。
さて解き方です。以下の通りマス目に記号を付けます。
ABCDE FGHIJ KLMNO PQRST UVWXY
以下、(記号、帽子の有無、見える帽子の数)で示します。
また、=で結んだ左右は順序を問わないものとします。
つまり(AB)=(有無)というのは(Aが有、Bが無)または(Aが無、Bが有)です。
(A?1)(B?3)(C?3)(D?3)(E?1) (F?3)(G?6)(H?5)(I?7)(J?4) (K?1)(L?5)(M?3)(N?4)(O?1) (P?3)(Q?7)(R?5)(S?7)(T?4) (U?2)(V?4)(W?3)(X?3)(Y?1)
(1)Iが7なのでCDEHJMNOの8人のうち、帽子をかぶっていないのは1人だけ。
(2)Eが1なのでDIJの3人のうち、帽子をかぶっているのは1人だけ。
共通するDJを考えると、(1)より帽子は有有か有無、(2)より帽子は有無か無無。
よって(DJ)=(有無)が確定し、(CEHMNO)が有、Iが無と判ります。
(A?1)(B?3)(C有3)(D?3)(E有1) (F?3)(G?6)(H有5)(I無7)(J?4) (K?1)(L?5)(M有3)(N有4)(O有1) (P?3)(Q?7)(R?5)(S?7)(T?4) (U?2)(V?4)(W?3)(X?3)(Y?1)
Dが3なのだが既に(CEH)が有なのでJは無
Jが4なのだが既に(I)が無なのでDは有
Oが1なのだが既に(N)が有なので(ST)は無
(A?1)(B?3)(C有3)(D有3)(E有1) (F?3)(G?6)(H有5)(I無7)(J無4) (K?1)(L?5)(M有3)(N有4)(O有1) (P?3)(Q?7)(R?5)(S無7)(T無4) (U?2)(V?4)(W?3)(X?3)(Y?1)
Sが7なのだが既に(T)が無なので(RWXY)は有
Yが1なのだが既に(ST)が無、(X)だけが?なので(X)は有
Nが4なのだが既に(IJST)が無、(R)だけが?なので(R)は有
(A?1)(B?3)(C有3)(D有3)(E有1) (F?3)(G?6)(H有5)(I無7)(J無4) (K?1)(L?5)(M有3)(N有4)(O有1) (P?3)(Q?7)(R有5)(S無7)(T無4) (U?2)(V?4)(W有3)(X有3)(Y有1)
(3)Qが7なので(KLPUV)は(有有有有無)
(4)Kが1なので(FGLPQ)は(有無無無無)
共通するLPを考えると、(3)より帽子は有有か有無、(4)より帽子は有無か無無。
よって(LP)=(有無)が確定し、(KUV)が有、(FGQ)が無と判ります。
(A?1)(B?3)(C有3)(D有3)(E有1) (F無3)(G無6)(H有5)(I無7)(J無4) (K有1)(L?5)(M有3)(N有4)(O有1) (P?3)(Q無7)(R有5)(S無7)(T無4) (U有2)(V有4)(W有3)(X有3)(Y有1)
Uが2なのだが既に(Q)が無なので(P)は有。よって(L)は無。
Aが1なのだが既に(FG)が無なので(B)は有。
Bが3なのだが既に(FG)が無なので(A)は有。
(A有1)(B有3)(C有3)(D有3)(E有1) (F無3)(G無6)(H有5)(I無7)(J無4) (K有1)(L無5)(M有3)(N有4)(O有1) (P有3)(Q無7)(R有5)(S無7)(T無4) (U有2)(V有4)(W有3)(X有3)(Y有1) ( 有 )( 有 )( 有 )( 有 )( 有 ) ( )( )( 有 )( )( ) ( 有 )( )( 有 )( 有 )( 有 ) ( 有 )( )( 有 )( )( ) ( 有 )( 有 )( 有 )( 有 )( 有 )
解答・その12
(ペンネ-ム:のっこん)
1行目のマスを左から順にA,B,C,D,E
2 〃 F,G,H,I,J
3 〃 K,L,M,N,O
4 〃 P,Q,R,S,T
5 〃 U,V,W,X,Y とする
そのマスにいる人が帽子をかぶっていれば○、
かぶっていなければ×と表わすことにする
1)Eが1であることに注目する
D,I,Jのうち、1つが○、2つが×である
Iが○、D・Jが×は「Iが7」に反する
Jが○、D・Iが×は「Jが4」に反する
よってDが○、I・Jが×である
Jが4、Iが7を勘案して
・ ・ ○○○ ・ ・ ○×× ・ ・ ○○○ ・・・[1] ・ ・ ・ ・ ・ ・ ・ ・ ・ ・
2)Yが1であることに注目する
S,T,Xのうち、1つが○、2つが×である
Sが○、T・Xが×は「Sが7」に反する
Tが○、S・Xが×は「Tが4」に反する
よってXが○、S・Tが×である
Tが4、Sが7を勘案して
・ ・ ・ ・ ・ ・ ・ ・ ・ ・ ・ ・ ○○○ ・・・[2] ・ ・ ○×× ・ ・ ○○○
[1]、[2]をあわせて
・ ・ ○○○ ・ ・ ○×× ・ ・ ○○○ ・ ・ ○×× ・ ・ ○○○
3)Aが1であることに注目する
B,F,Gのうち、1つが○、2つが×である
Gが○、B・Fが×は「Mが3」に反する
Fが○、B・Gが×は「Cが3」に反する
よってBが○、F・Gが×である
・ ○ ○○○
× × ○××
・ ・ ○○○
・ ・ ○××
・ ・ ○○○
4)Kが1であることに注目する
L,P,Qのうち、1つが○、2つが×である
Lが○、P・Qが×は「Uが2」に反する
Qが○、L・Pが×は「Qが7」に反する
よってPが○、L・Qが×である
Fが3、Qが7を勘案して
○○○○○ ××○×× ○×○○○ ○×○×× ○○○○○
表れた文字は「正」である
解答・その13
(ペンネ-ム:夜ふかしのつらいおじさん)
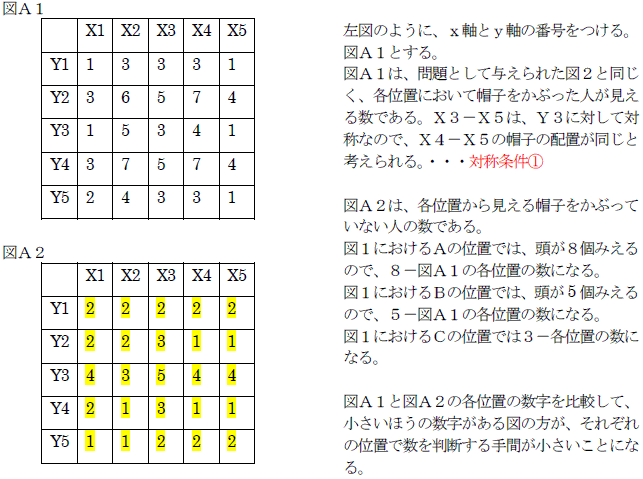
●マス目の位置をエクセルのように、左からA列、B列、・・・上から1行、2行、・・・とします。(図1)
図2のように、25個のマス目を、角(桃色)、辺(空色)、面(黄色)に分けて考えます。
1個のマス目の周りには、角だと3個、辺だと5個、面だと8個のマス目があります。
つまり、帽子をかぶっている人が角にいれば3回、辺にいれば5回、面にいれば8回数えられます。
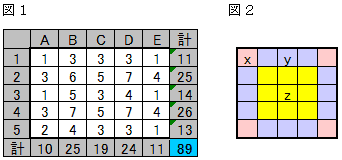
●帽子をかぶっている人が角にx人、辺にy人、面にz人いるとすると、次の方程式が成り立ちます。
3x+5y+8z=89 ・・・・・・ (1)
ここで、C3=3に注目すると、面で帽子をかぶっている人数は3か4です。
・z=3とすると、(1)は、3x+5y=65です。
この方程式の解は、nを整数として、(x, y)=(5+5n ,10-3n) です。
角は4個しかないので、xは、n=-1のときだけ成立します。
しかし、そのときy=13となり辺は12個しかないので、z=3は不適当です。
・z=4とすると、(1)は、3x+5y=57です。
この方程式の解は、(x , y)=(4+5n ,9-3n) です。
n=0のとすると、(x , y , z)=(角,辺,面)=(4 , 9 , 4)となります。
つまり、角の人は4人とも帽子をかぶっています。(図3)
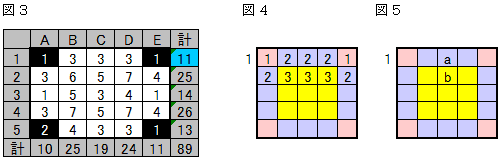
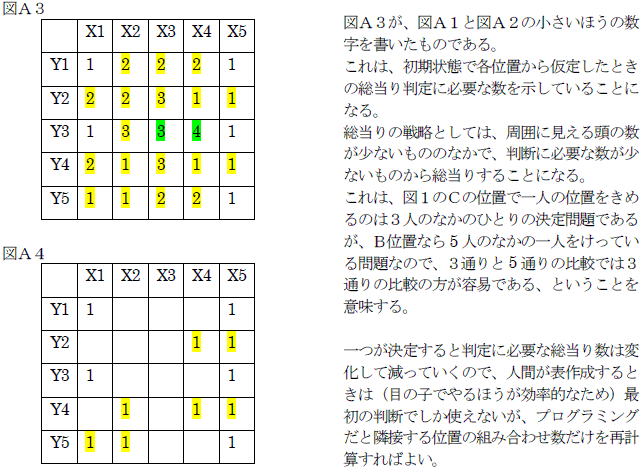
●1行目の合計のことを考えます。
図4のマス目の数は、その場所の帽子をかぶっている人が1行目の人に何回数えられるかを表しています。
1・2行目で帽子をかぶっている人が角に2人、辺にa人、面にb人いるとすると、次の方程式が成り立ちます。
1×2+2a+3b=11 つまり、 2a+3b=9 ・・・・・・ (2)
この方程式の解は、(a, b)=(3+3n , 1-2n) です。
可能性があるのは、n=-1, 0のとき、つまり、(a, b)=(0, 3)、 (3, 1)です。
しかし、D2=7なので、(a, b)=(0, 3)は成立しません。
(a, b)=(辺,面)=(3, 1)となります。
C1=3なので、b=1(面に1人)なので、B1、D1の人は帽子をかぶっています。
A1=E1=1なので、C1、C2の人は帽子をかぶっています。(図6)
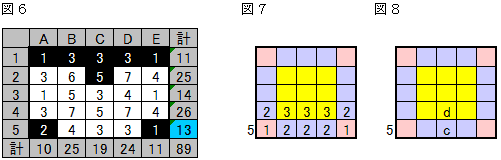
●5行目の合計のことを考えます。
図7では、帽子をかぶっている人が5行目の人に何回数えられるかをマス目の数で表しています。
4・5行目で帽子をかぶっている人が角に2人、辺にc人、面にd人いるとすると、次の方程式が成り立ちます。
1×2+2c+3d=13 つまり、2c+3d=11
この方程式の解は、 です。
可能性があるのは、n=0,1のとき、つまり、(c, d)=(1, 3)、(4, 1)です。
しかし、B4=D4=7なので、(c, d)=(1, 3)は成立しません。
(c, d)=(辺,面)=(4, 1)となります。
B4=D4=7になので、C4の人は帽子をかぶっています。
C5=3なので、B5、D5の人は帽子をかぶっています。
A5=2、E5=1なので、A4、C5の人が帽子をかぶっています。(図9)
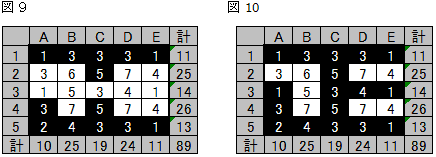
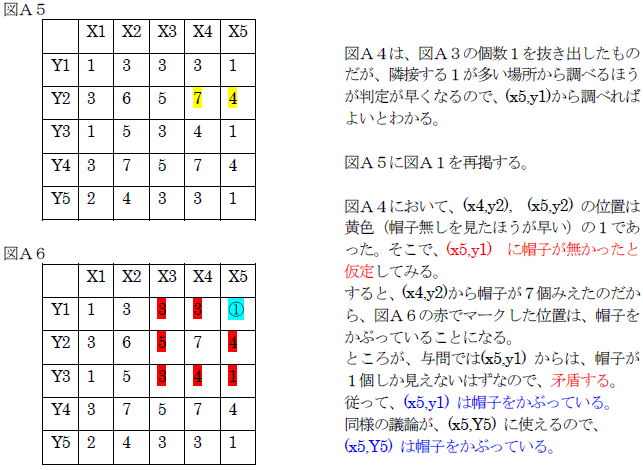
●ここまでで、(x , y , z)=(角,辺,面)=(4 , 9 , 4)のうち角は4個、辺は7個、面は2個決まりました。
残りは、辺が2個、面が2個です。
辺は、残りがA3、E3しかないので決まります。
面は、B4=D2=D4=7なので、C3、D3と決まります。(図10)
答えは「正」です。
●この問題は右のようにしても良いと思います。

解答・その14
(ペンネ-ム:浜田 明巳)
エクセルのマクロで解きました.覆面算の要領です.答は「正」の字となります.
Option Explicit
'1 3 3 3 1
'3 6 5 7 4
'1 5 3 4 1
'3 7 5 7 4
'2 4 3 3 1
'a11 a12 a13 a14 a15
'a21 a22 a23 a24 a25
'a31 a32 a33 a34 a35
'a41 a42 a43 a44 a45
'a51 a52 a53 a54 a55 (aij=0,1)
Sub Macro1()
Sheets("Sheet1").Select
Dim a11 As Integer
Dim a12 As Integer
Dim a13 As Integer
Dim a14 As Integer
Dim a15 As Integer
Dim a21 As Integer
Dim a22 As Integer
Dim a23 As Integer
Dim a24 As Integer
Dim a25 As Integer
Dim a31 As Integer
Dim a32 As Integer
Dim a33 As Integer
Dim a34 As Integer
Dim a35 As Integer
Dim a41 As Integer
Dim a42 As Integer
Dim a43 As Integer
Dim a44 As Integer
Dim a45 As Integer
Dim a51 As Integer
Dim a52 As Integer
Dim a53 As Integer
Dim a54 As Integer
Dim a55 As Integer
Dim gyou As Integer '解の表示開始行
Cells(1, 1).Value = 0 '解の個数
Range("A1").Select
For a11 = 0 To 1
For a12 = 0 To 1
For a13 = 0 To 1
For a14 = 0 To 1
For a15 = 0 To 1
For a21 = 0 To 1
a22 = 1 - a12 - a21
If a22 = 0 Or a22 = 1 Then
a23 = 3 - a11 - a13 - a21 - a22
If a23 = 0 Or a23 = 1 Then
a24 = 3 - a12 - a14 - a22 - a23
If a24 = 0 Or a24 = 1 Then
a25 = 3 - a13 - a15 - a23 - a24
If (a25 = 0 Or a25 = 1) And a14 + a24 + a25 = 1 Then
For a31 = 0 To 1
a32 = 3 - a11 - a12 - a22 - a31
If a32 = 0 Or a32 = 1 Then
a33 = 6 - a11 - a12 - a13 - a21 - a23 - a31 - a32
If a33 = 0 Or a33 = 1 Then
a34 = 5 - a12 - a13 - a14 - a22 - a24 - a32 - a33
If a34 = 0 Or a34 = 1 Then
a35 = 7 - a13 - a14 - a15 - a23 - a25 - a33 - a34
If (a35 = 0 Or a35 = 1) And a14 + a15 + a24 + a34 + a35 = 4 Then
For a41 = 0 To 1
a42 = 1 - a21 - a22 - a32 - a41
If a42 = 0 Or a42 = 1 Then
a43 = 5 - a21 - a22 - a23 - a31 - a33 - a41 - a42
If a43 = 0 Or a43 = 1 Then
a44 = 3 - a22 - a23 - a24 - a32 - a34 - a42 - a43
If a44 = 0 Or a44 = 1 Then
a45 = 4 - a23 - a24 - a25 - a33 - a35 - a43 - a44
If (a45 = 0 Or a45 = 1) And a24 + a25 + a34 + a44 + a45 = 1 Then
For a51 = 0 To 1
a52 = 3 - a31 - a32 - a42 - a51
If (a52 = 0 Or a52 = 1) And a41 + a42 + a52 = 2 Then
a53 = 7 - a31 - a32 - a33 - a41 - a43 - a51 - a52
If (a53 = 0 Or a53 = 1) And a41 + a42 + a43 + a51 + a53 = 4 Then
a54 = 5 - a32 - a33 - a34 - a42 - a44 - a52 - a53
If (a54 = 0 Or a54 = 1) And a42 + a43 + a44 + a52 + a54 = 3 Then
a55 = 7 - a33 - a34 - a35 - a43 - a45 - a53 - a54
If (a55 = 0 Or a55 = 1) And a34 + a35 + a44 + a54 + a55 = 4
And a43 + a44 + a45 + a53 + a55 = 3
And a44 + a45 + a54 = 1 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = Cells(1, 1).Value * 6 - 5
Call sell(gyou, 2, a11)
Call sell(gyou, 3, a12)
Call sell(gyou, 4, a13)
Call sell(gyou, 5, a14)
Call sell(gyou, 6, a15)
Call sell(gyou + 1, 2, a21)
Call sell(gyou + 1, 3, a22)
Call sell(gyou + 1, 4, a23)
Call sell(gyou + 1, 5, a24)
Call sell(gyou + 1, 6, a25)
Call sell(gyou + 2, 2, a31)
Call sell(gyou + 2, 3, a32)
Call sell(gyou + 2, 4, a33)
Call sell(gyou + 2, 5, a34)
Call sell(gyou + 2, 6, a35)
Call sell(gyou + 3, 2, a41)
Call sell(gyou + 3, 3, a42)
Call sell(gyou + 3, 4, a43)
Call sell(gyou + 3, 5, a44)
Call sell(gyou + 3, 6, a45)
Call sell(gyou + 4, 2, a51)
Call sell(gyou + 4, 3, a52)
Call sell(gyou + 4, 4, a53)
Call sell(gyou + 4, 5, a54)
Call sell(gyou + 4, 6, a55)
End If
End If
End If
End If
Next a51
End If
End If
End If
End If
Next a41
End If
End If
End If
End If
Next a31
End If
End If
End If
End If
Next a21
Next a15
Next a14
Next a13
Next a12
Next a11
End Sub
Sub sell(ByVal x As Integer, ByVal y As Integer, ByVal a As Integer)
If a Then
Cells(x, y).Value = "●"
Else
Cells(x, y).Value = "○"
End If
End Sub
解答・その15
(ペンネ-ム:紀伊龍洸)
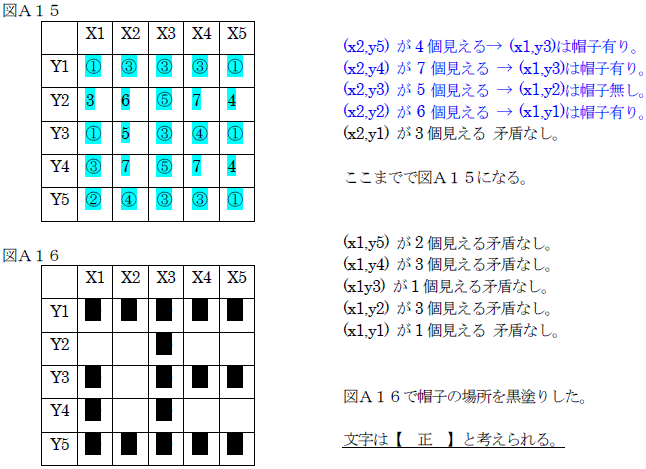
解答・その16
(ペンネ-ム:kazz)
<問題図>
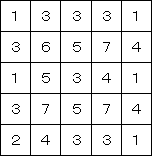
まず、右上の3×3部分に注目。
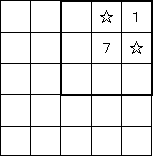
7の周囲8マスのうち、塗らないマスが1つ。
右上に1があるため、2つの☆を両方塗ることはできない。
よって残りの6マスは塗るマスに決定。

同じ要領で、右下の3×3部分の7と右下の1に注目して塗るマスを決定。
右中央の1に注目すると、左隣のマスが塗られているので残りのマスは塗らないマスに決定。
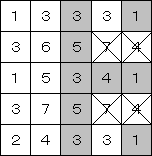
すると、右上・右下の1で塗るマスが左隣のマスに決定。
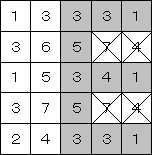
左下の7とその左上の1についても同様に考える。
この1は右隣・下隣のいずれかで塗られるので、その他のマスは塗らないマスに決定。
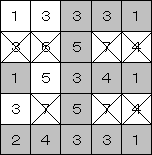
7のマスは塗らないので、左下の2で上隣のマスが塗るマスに決定。
同時に、1の右隣は塗らないマスに決定。
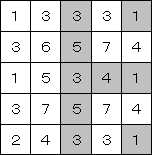
最後、6に注目。残りの2マスは塗るマスに決定。
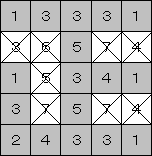
完成!できた漢字は「正」。
全てのマスにヒントがありましたが、1,2,6,7のヒントだけで解くことができました。
解答・その17
(ペンネ-ム:T_Tatekawa)
| 1 | 3 | 3 | 3 | 1 |
| 3 | 6 | 5 | 7 | 4 |
| 1 | 5 | 3 | 4 | 1 |
| 3 | 7 | 5 | 7 | 4 |
| 2 | 4 | 3 | 3 | 1 |
1) まず,右下の7に注目.その右下に1があるので,
1の上の4か,左の3のいずれかは帽子をかぶっていない.
以下,漢数字は帽子をかぶっている人とする.
| 1 | 3 | 3 | 3 | 1 |
| 3 | 6 | 5 | 7 | 4 |
| 1 | 5 | 三 | 四 | 一 |
| 3 | 7 | 五 | 7 | 4 |
| 2 | 4 | 三 | 3 | 一 |
2) 右下の3から見ると,既に周囲に帽子をかぶっている人が3人
いるので,3の右上の人は帽子をかぶっていない.よって
3のところの人が帽子をかぶっている.
| 1 | 3 | 3 | 3 | 1 |
| 3 | 6 | 5 | 7 | 4 |
| 1 | 5 | 三 | 四 | 一 |
| 3 | 7 | 五 | 7 | 4 |
| 2 | 4 | 三 | 三 | 一 |
3) 右端中段の一からは四だけが見えているので,他は帽子をかぶって
いない.すると,四のところからは左上の5の人が帽子をかぶって
いなければならない.
この条件から上段右から2番目の3の人も,帽子をかぶっている.
その下の7の条件を当てはめると以下の様になる.
| 1 | 3 | 三 | 三 | 一 |
| 3 | 6 | 五 | 7 | 4 |
| 1 | 5 | 三 | 四 | 一 |
| 3 | 7 | 五 | 7 | 4 |
| 2 | 4 | 三 | 三 | 一 |
4) 左下の7の条件を.1) と同様に考えてまず当てはめる.
| 1 | 3 | 三 | 三 | 一 |
| 3 | 6 | 五 | 7 | 4 |
| 1 | 5 | 三 | 四 | 一 |
| 3 | 7 | 五 | 7 | 4 |
| 二 | 四 | 三 | 三 | 一 |
5) 中央下から2番目の五を考えると,左端の3の人が帽子をかぶっている.
| 1 | 3 | 三 | 三 | 一 |
| 3 | 6 | 五 | 7 | 4 |
| 1 | 5 | 三 | 四 | 一 |
| 三 | 7 | 五 | 7 | 4 |
| 二 | 四 | 三 | 三 | 一 |
6) この三から見ると,すぐ上の1の人が帽子をかぶっている.
| 1 | 3 | 三 | 三 | 一 |
| 3 | 6 | 五 | 7 | 4 |
| 一 | 5 | 三 | 四 | 一 |
| 三 | 7 | 五 | 7 | 4 |
| 二 | 四 | 三 | 三 | 一 |
6) 5)で置き換えた一の条件,6の条件を満たすのは以下の通り.
| 一 | 三 | 三 | 三 | 一 |
| 3 | 6 | 五 | 7 | 4 |
| 一 | 5 | 三 | 四 | 一 |
| 三 | 7 | 五 | 7 | 4 |
| 二 | 四 | 三 | 三 | 一 |
解答・その18
(ペンネ-ム:Asterisk*)
左側を解くのが楽しかったです。
正の字です。>
解答・その19
(ペンネ-ム:まろん)
こういう、機械的な手順で解けそうな問題は、コンピューターを使うことで、
人間が頭をひねらなくても簡単に解けそうなのでやってみました。
その解き方ですが、帽子の個数およびかぶり方について全てのパターン (以
後、個々のパターンを仮説と呼びます) を生成 (generate) し、問題文の図
2 にある制約条件に当てはまるかどうかを検査(test)し、正しい仮説のみを
選ぶことにより全ての解を得る、という方法 (generate and test)を用いま
した。
通常、この方法では、仮説の生成の途中でも、その仮説が制約条件に当ては
まらないと証明できる場合には、その仮説についての残りの計算を破棄した
り(枝刈り)(*1)、ヒューリスティクスなどの利用により有望な仮説のみ生成
する(*2)など、計算量を節約するための工夫をするのですが、本問題はあま
りに規模が小さい(*3)ので、こういった工夫は不要で、総当たりでも現実的
な時間内で解くことができそうと予想立て、まずは何も工夫をせずに実装し
てみました。
なにも複雑な事はしていないので、プログラムは 15分ほどで完成、実行する
と3秒足らずで答えが出ました。コンピューターさまさまです。
なお、黒く塗るのは面倒なので、#の文字で代用しています。
答え:
解は、ただひとつで、以下の通りです。「正」の字ですね。
# # # # #
#
# # # #
# #
# # # # #
*1 例えば、問題文の制約条件により、左上の升目は1ですが、この制約から、 「帽子の総数は 1以上」という新しい制約条件を導出できます。従って「帽 子の総数が 0個(当然誰もかぶっていない)」という仮説はこの新しい制約条 件を利用すれば「数の大小の判定」という、とても簡単な検査により棄却で きます。これは、問題文にある制約条件を満たすかどうかを厳密に検査する よりも素早く行えますし、 (手順にもよりますが、) 仮説の生成途中でもこ の検査は実行できる場合が有りますから、早めの検査を行えば、全体として は高速にできる可能性があるわけです。
*2 「帽子の総数は 1以上」という制約条件から、そもそも、帽子の総数が0 個であるような仮説を生成しないような手順(アルゴリズム)を組めば、もっ と高速化できます。こういった、「知恵」を手順そのものなどに組み込むこ とも、しばしば行われます。
*3 この問題では、全ての帽子のかぶり方のパターンは、たったの 225通り
です。ところが、これが、6x6になったりしたら、(一路広くなるだけですが)
全パターンは236となり、なんらかの高速化のための工夫が必要になるとこ
でした。
付録: プログラムリスティング
#include#include #include #include struct board { int v[7][7]; }; static void generate(struct board *, unsigned int); static int test(struct board const *); static int count_hats(struct board const *, int, int); static void print(struct board const *, FILE *); static struct board cnst = { { {0, 0, 0, 0, 0, 0, 0}, {0, 1, 3, 3, 3, 1, 0}, {0, 3, 6, 5, 7, 4, 0}, {0, 1, 5, 3, 4, 1, 0}, {0, 3, 7, 5, 7, 4, 0}, {0, 2, 4, 3, 3, 1, 0}, {0, 0, 0, 0, 0, 0, 0}, } }; int main() { unsigned int x; for (x = 0; x < 1024 * 1024 * 32; x++) { struct board stat; generate(&stat, x); if (test(&stat)) { print(&stat, stdout); } } return 0; } static void generate(stat, x) struct board *stat; unsigned int x; { int j, i, k; j = i = 1; memset(stat, 0, sizeof *stat); for (k = 0; k < 25; k++, x >>= 1) { stat->v[j][i++] = x & 1; if (i >= 6) { j++; i = 1; } } } static int test(stat) struct board const *stat; { int j, i; for (j = 1; j <= 5; j++) { for (i = 1; i <= 5; i++) { if (count_hats(stat, j, i) != cnst.v[j][i]) { return 0; } } } return 1; } static int count_hats(stat, j, i) struct board const *stat; { int l, k, hats; hats = 0; for (l = -1; l <= 1; l++) { for (k = -1; k <= 1; k++) { if (!(l == 0 && k == 0) && stat->v[j + l][i + k]) { hats++; } } } return hats; } static void print(stat, stream) struct board const *stat; FILE *stream; { int j, i; for (j = 1; j <= 5; j++) { for (i = 1; i <= 5; i++) { fprintf(stream, " %c", stat->v[j][i] ? '#' : ' '); } fprintf(stream, "\n"); } }
解答・その20
(ペンネ-ム:オヤジ)
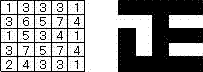
∴ 正
解答・その21
(ペンネ-ム:三角定規)
帽子をかぶっている人は,図の通りです。手探りでやりました。現れる文字は,「正」ですね。
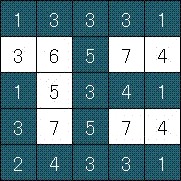
コメント
25個あるマス目を1つづつ、条件を使って、白黒判定をしていきますが、 コツがあるとしたら、角や端を狙う(ジグソーパズルのようですね)のと、 大きい数字に着目するということでしょうか。
 top
top