栤戣192丂儅僢僠朹偺栤戣丒偦偺俀
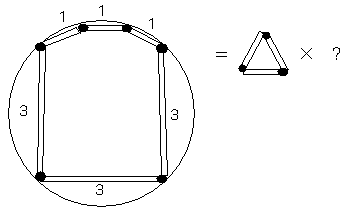
挿偝侾cm偺儅僢僠俁杮偲丄俁cm偺儅僢僠俁杮傪丄壓偺恾偺傛偆偵墌偵増偆傛偆偵偍偒傑偡丅
偙偺俇妏宍偺柺愊偼丄侾cm偺儅僢僠俁杮偱彂偄偨惓俁妏宍偺柺愊偺壗攞偁傞偱偟傚偆偐丅
栤戣偺弌揟
僷僘儖傛傝柺敀偄拞妛擖帋偺嶼悢
僺乕僞乕丒僼儔儞僋儖
島択幮
夝摎
乣摓拝弴偵偛徯夘偟傑偡乣
夝摎丒偦偺1
乮儁儞僱亅儉丗師榊挿乯
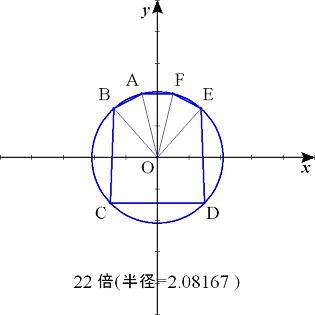
塃忋偺揰傪俙偲偟丄斀帪寁廃傝偵俛丆俠丆俢丄壓曈偺2揰傪俤丆俥偲偟丄墌偺拞怱傪俷偲偟傑偡丅
偡傞偲丄仮俷俙俛丄仮俷俛俠丄仮俷俠俢偼崌摨
仮俷俙俥丄仮俷俥俤丄仮侽俤俢傕崌摨乮偦傟偧傟3曈偺挿偝偑摨偠乯
偦偙偱丄仮俷俛俙偲仮俷俙俥傪懌偟偨傕偺丄偮傑傝巐妏宍俷俛俙俥偱峫偊傞偲丄
妏俛俷俥偼120搙偱丄巐妏宍俷俛俙俥偼6妏宍俙俛俠俢俤俥偺侾乛俁
巆傝偺嶰妏宍係偮(仮俷俛俠丄仮俷俢俤側偳乯傪偽傜偟偰偔偭偮偗偰丄
巐妏宍俷俛俙俥偲崌摨偺巐妏宍傪俀偮嶌傝丄偆傑偔崌傢偣傞偲丄
侾曈俆偺惓嶰妏宍偐傜丄俁偮偺捀揰偐傜侾曈侾偺惓嶰妏宍傪俁偮
旘偽偟偨僟僀儎儌儞僪偺傛偆側俇妏宍偑弌棃傑偡丅
偙傟偼丄俀俆亅俁亖俀俀攞偱偡偹
夝摎丒偦偺2
乮儁儞僱亅儉丗儅僔儍乯
傑偢, 墌偺拞怱傪偐傜奺捀揰(儅僢僠朹偺愭)偛偲偵愗傝傑偡.
師偵儅僢僠朹侾偲俁偱偱偒偨愵宍傪岎屳偵暲傋傑偡.
偡傞偲侾僙僢僩偺愵宆偺拞怱妏偼120搙偵側傝傑偡.
堦曽, 偦偺斀懳偺妏搙偼360-120=240搙偵側傝傑偡.
墌廃妏偺掕棟傛傝, 儅僢僠朹侾偲俁偐傜側傞妏搙偼240/2=120搙偱偡.
偙偺儅僢僠朹侾偺奜懁偵儅僢僠朹侾偐傜側傞惓嶰妏宍傪抲偒傑偡.
偡傞偲, 妏搙偑惓嶰妏宍偲儅僢僠朹俁偐傜側傞妏搙偑180搙,偮傑傝捈慄偵側傝傑偡.
偙偺憖嶌傪慡偰偺儅僢僠朹侾偵懳偟偰峴偆偲
慡懱偺宍偼儅僢僠朹俆偺惓嶰妏宍偵側傝傑偡.
偙偺柺愊偼儅僢僠朹侾偐傜側傞惓嶰妏宍偺25攞偱偡.
傑偨, 捛壛偟偨柺愊偑俁偮暘側偺偱,
摎偊偼, 22攞偱偡.
夝摎丒偦偺3
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
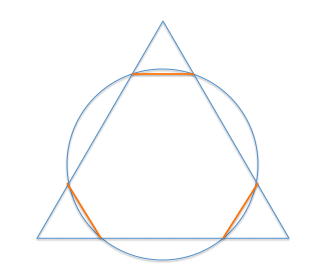
儅僢僠朹偺埵抲傪擖傟懼偊偰丄恾偺傛偆側榋妏宍傪嶌傞丅
偦偺奜懁偵丄彫偝偄惓嶰妏宍傪偔偭偮偗傞偲丄1曈偑5偺惓嶰妏宍偵側傞偺偱...
媮傔傞柺愊偼...彫偝偄惓嶰妏宍偺...
52-3=22 攞 侓
夝摎丒偦偺4
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
亂偦偺侾亃
恾侾偺傛偆偵儅僢僠朹偺抂偲墌偺拞怱傪寢傃傑偡丅
師偵恾俀偺傛偆偵嶰妏宍傪岎屳偵暲傃懼偊傑偡丅
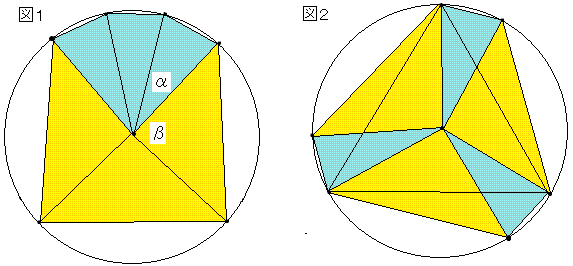
偝傜偵恾俁偺傛偆偵墌偵撪愙偡傞戝偒側惓嶰妏宍偲嵶挿偄嶰妏宍偵暘偗偰峫偊傑偡丅
恾係偺傛偆偵嵶挿偄嶰妏宍傪暲傃懼偊偰拞偑敳偗偨惓嶰妏宍傪偮偔傝傑偡丅
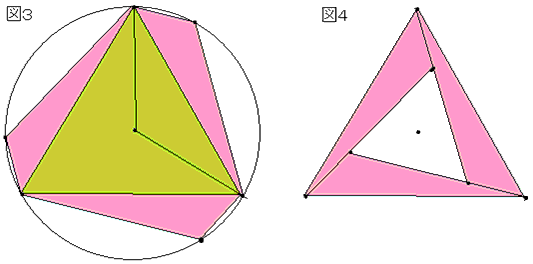
偝偰丄僺儞僋怓偺嶰妏宍偺擇曈偼侾偲3偱偦偺娫偺妏偼120搙偱偡丅
乮墌偵撪愙偡傞嶰妏宍偺岦偐偄崌偆妏偺榓偼180搙偱偡乯
僺儞僋怓偺嶰妏宍偺堦斣挿偄曈偺挿偝 偼丄梋尫掕棟傛傝


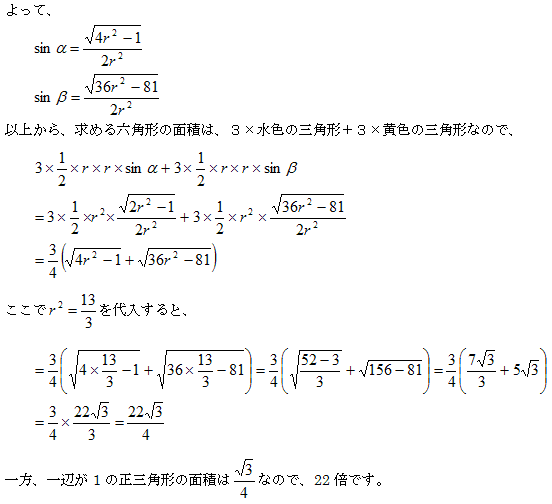
夝摎丒偦偺5
乮儁儞僱亅儉丗Ryu1128乯
栤戣偺6妏宍傪墌偺拞怱偲奺撪愙揰傪寢傫偩慄偱暘妱偟墌撪偱慻傒懼偊傑偡丅
偡傞偲丄壓恾偺傛偆偵侾曈偑5偺惓嶰妏宍偺俁嬿偐傜侾曈侾偺惓嶰妏宍傪庢傝彍偄偨俇妏宍偲側傝傑偡丅
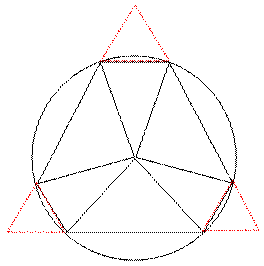
侾曈偑5偺惓嶰妏宍偼侾曈侾偺惓嶰妏宍偺俀俆攞側偺偱丄
栤戣偺6妏宍偺柺愊偼侾曈侾偺惓嶰妏宍偺25-3亖22攞偲側傝傑偡丅
夝摎丒偦偺6
乮儁儞僱亅儉丗傑乕傝傫倎値倓偝偲傝傫乯
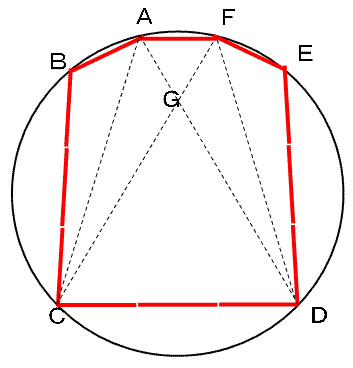 恾偺偲偍傝曗彆慄傪偲傝丄奺揰傪俙丄俛丄俠丄俢丄俤丄俥丄俧偲偍偔丅
恾偺偲偍傝曗彆慄傪偲傝丄奺揰傪俙丄俛丄俠丄俢丄俤丄俥丄俧偲偍偔丅
偙偙偱丄仮俙俛俠偲仮俙俧俠偵拝栚偡傞偲
丂丂曈俙俠嫟捠
丂丂佢俛俙俠亖佢俧俙俠乮嫙偵尫偺挿偝俁偺墌廃妏乯
丂丂佢俙俠俛亖佢俙俠俧乮嫙偵尫偺挿偝侾偺墌廃妏乯
侾曈椉抂妏偑摍偟偄偺偱
丂丂仮俙俛俠佭仮俙俧俠
傛偭偰俙俧亖俙俛亖侾丄俠俧亖俠俛亖俁
摨偠偔俥俧亖侾丄俢俧亖俁
埲忋傛傝丄
仮俙俥俧偼侾曈偺挿偝偑侾偺惓嶰妏宍
仮俠俧俢偼侾曈偺挿偝偑俁偺惓嶰妏宍
侾曈偑侾偺惓嶰妏宍偺柺愊傪兛偲偡傞偲
仮俙俥俧偺柺愊偼兛
仮俠俧俢偺柺愊偼俋兛
仮俙俧俠偺柺愊偼仮俠俢俧偺柺愊偺侾乛俁乮AG/DG乯偵側傞偺偱丄俁兛
仮俙俧俠佭仮俙俛俠佭仮俥俧俢佭仮俥俤俢側偺偱
仮俙俛俠丄仮俥俧俢丄仮俥俤俢偺柺愊傕俁兛
傛偭偰俇妏宍俙俛俠俢俥俥偺柺愊偼丂乮侾亄俋亄係亊俁乯兛亖俀俀兛
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂摎丏俀俀屄
夝摎丒偦偺7
乮儁儞僱亅儉丗haya乯
摎丗 22攞
亂夝偒曽亃

夝摎丒偦偺8
乮儁儞僱亅儉丗偺偭偙傫乯
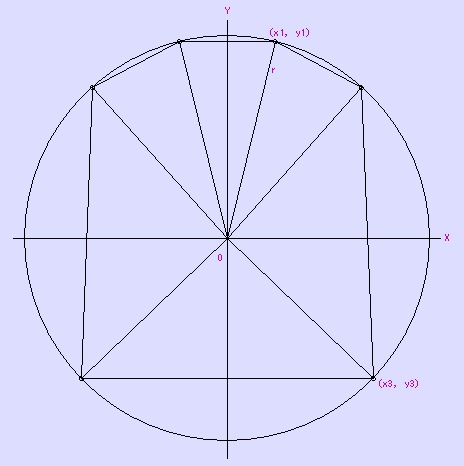
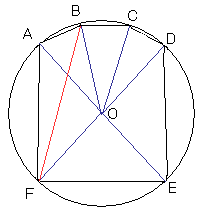 堦斣嵍偵偁傞1cm偺儅僢僠朹偺嵍抂傪A偲偟
帪寁夞傝偵奺捀揰傪B,C,D,E,F偲偡傞
堦斣嵍偵偁傞1cm偺儅僢僠朹偺嵍抂傪A偲偟
帪寁夞傝偵奺捀揰傪B,C,D,E,F偲偡傞
偙偺墌偺拞怱傪O偲偟丄OA=r 偲偡傞
仮OAB,仮OBC,仮OCD偼崌摨側擇摍曈嶰妏宍
仮ODE,仮OEF,仮OFA偼崌摨側擇摍曈嶰妏宍
傛偭偰巐妏宍BAFO偺柺愊偼榋妏宍偺柺愊偺1/3
傑偨佢BOF=360亱亐3亖120亱
佢OBA=佢OAB=兛丄佢OAF=佢OFA=兝偲偡傞偲
2乮兛亄兝乯亖360亱-120亱亖240亱偩偐傜 兛亄兝亖120亱
偮傑傝佢BAF=120亱
仮BAF偵偍偄偰
BF2=12+32-2丒1丒3丒cos120亱
廬偭偰BF2=13
仮BFO偵偍偄偰
BF2=倰2+r2-2丒r丒r丒cos120亱
廬偭偰r2=13/3
仮BAF=(1/2)丒1丒3丒sin120亱=3併3/4(cm2)
仮BFO=(1/2)丒r2丒sin120亱=13併3/12(cm2)
傛偭偰 3(仮BAF+仮BFO)=22併3/4(cm2)
1cm偺儅僢僠朹3杮偱偱偒傞惓嶰妏宍偺柺愊偼併3/4(cm2)偩偐傜
乮榋妏宍偺柺愊乯亐乮惓嶰妏宍偺柺愊乯亖22丂
丂丂
夝摎丒偦偺9
乮儁儞僱亅儉丗偪傚傠傫偼懢懢乯

夝摎丒偦偺10
乮儁儞僱亅儉丗揮埵斀墳乯
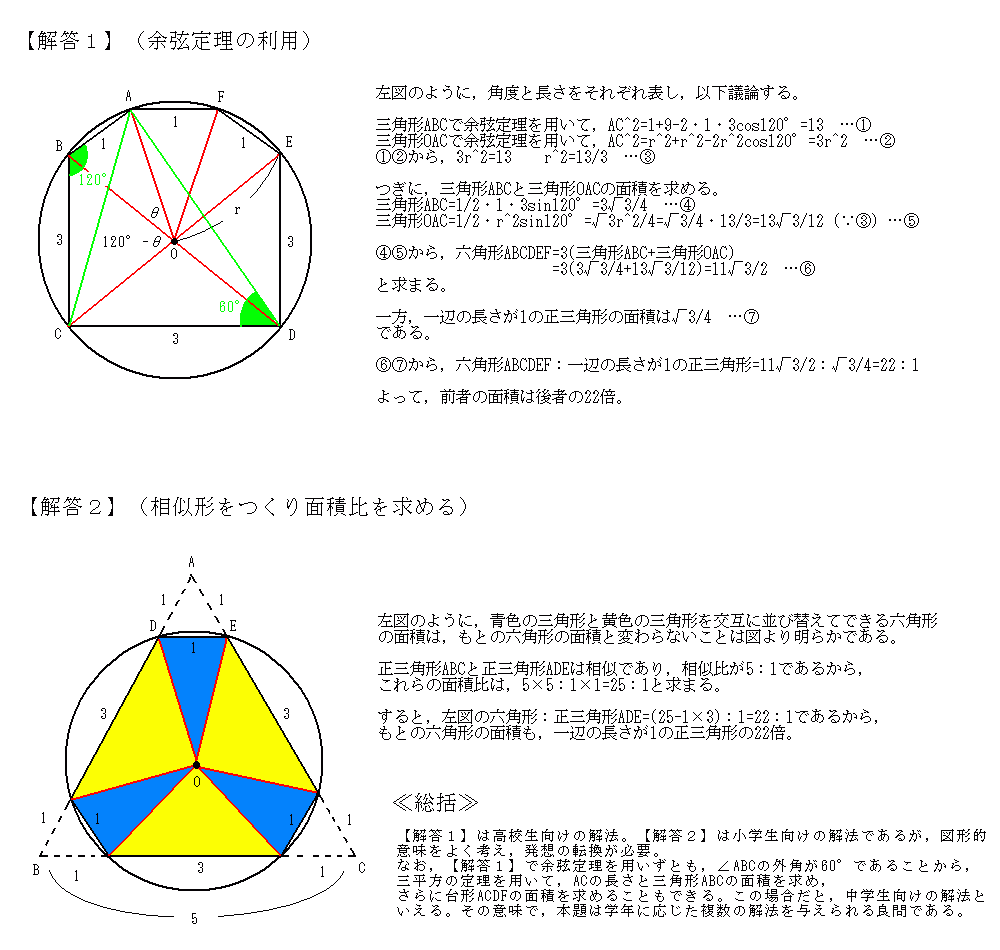
亂夝朄嘥亃嶰妏娭悢傪梡偄傞曽朄
栤戣偺弌揟傪尒偰偄側偐偭偨偺偱丄拞妛擖帋栤戣偲偼巚傢偢偵嶰妏娭悢傪巊偄傑偟偨丅
榋妏宍偼師偺擇庬椶偺嶰妏宍俙丄俛丄偦傟偧傟嶰偮偐傜峔惉偝傟偰偄傞丅
梌偊傜傟偨墌偺敿宎傪r丄嶰妏宍俙丄俛偺捀妏傪偦傟偧傟兛丄兝丄
偝傜偵丄捀揰偐傜掙曈偵壓偟偨悅慄偺挿偝傪偦傟偧傟丄h1丄h2偲偡傞丅
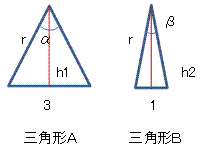
嶰妏宍俙偵偮偄偰
丂丂r sin (兛/2) =3/2丂丂丒丒丒嘆
嶰妏宍俛偵偮偄偰
丂丂r sin (兝/2) =1/2丂丂丂丒丒丒嘇
偙偙偱丄3兛亄3兝亖2兾丂側偺偱丄兝/2亖兾/3-兛/2
丂丂丂r sin (兝/2)
丂丂=r sin (兾/3-兛/2)
丂丂=r {sin (兾/3)丒cos (兛/2)-cos (兾/3)丒sin (兛/2)}
丂丂=r {併3/2丒cos (兛/2)-1/2丒sin (兛/2)}
偙偙偱丄cos (兛/2)={1-sin2(兛/2)}1/2丂偱偁傞偐傜
丂丂=r[併3/2丒{1-sin2(兛/2)}1/2-1/2丒sin (兛/2)]丂丂丒丒丒嘇'
幃嘆嘇'傛傝丄r 偵偮偄偰夝偔偲
丂丂倰2亖13/3
亪丂r>0傛傝丄丂倰亖(13/3)1/2
偙偺r 傪梡偄偰丄嶰暯曽偺掕棟偐傜h1,h2傪媮傔傞偲師偺捠傝丅
丂丂h1=併3丒5/6
丂丂h2=併3丒7/6
傛偭偰丄嶰妏宍俙丄俛偺柺愊傪偦傟偧傟俽A丂丄俽B偲偡傞偲
丂丂俽A=併3丒5/4
丂丂俽B=併3丒7/12
亪榋妏宍偺柺愊偼丄3俽A+3俽B亖併3丒11/2
懠曽丄堦曈偑1們倣偺惓嶰妏宍偺柺愊偼丄俽1=併3/4
亪丂(3俽A+3俽B)/俽1亖22
亂夝朄嘦亃嶰妏娭悢傪梡偄側偄曽朄
拞妛擖帋栤戣側偺偱嶰妏娭悢傪巊傢側偄曽朄偱夝偒傑偟偨丅
夝朄嘥偱弎傋偨捠傝丄榋妏宍偼擇庬椶偺嶰妏宍偱峔惉偝傟偰偄傞丅
偦偺擇庬椶偺嶰妏宍偐傜壓婰偺巐妏宍傪慻傒棫偰傞偙偲偑偱偒傞偑丄
偙偺巐妏宍偼榋妏宍偺晹暘峔憿偱偁傝丄柺愊偼榋妏宍偺1/3偱偁傞丅
曈BC傪墑挿偟偰丄捀揰A偐傜壓偟偨悅慄偲偺岎揰傪D偲偡傞偲丄
佢AOC=120亱偱偁傞偐傜丄墌廃妏偺掕棟偵傛傝丄佢ABC亖120亱
傛偭偰丄佢ABD=60亱丄佢BAD=30亱
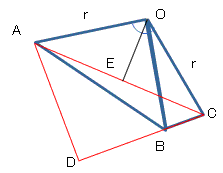
仮ABD偵偮偄偰丄BD丗AB丗AD亖侾丗俀丗併3
亪BD亖3/2丄AD亖併3丒3/2丂(佹 AB=3)
仮ACD偵偮偄偰丄CD=5/2側偺偱丄嶰暯曽偺掕棟偵傛傝丄AC=併13
傑偨丄仮OAC偼擇摍曈嶰妏宍側偺偱丄佢OAC=佢OCB=30亱
捀揰O偐傜曈AC傊悅慄傪壓偟丄偦偺岎揰傪E偲偡傞偲丄
仮OAE偵偮偄偰丄EO丗AO丗AE亖侾丗俀丗併俁丂偱偁傞偐傜丄E0=併39丒1/6
偙傟偱柺愊傪媮傔傞弨旛偑惍偭偨丅
仮OAC偺柺愊S1=AC亊E0亊1/2=併3丒13/12
仮ABC偺柺愊S2=仮ACD偺柺愊S3-仮ABD偺柺愊S4=併3丒3/4
亪S1+S2=併3丒11/6
亪榋妏宍偺柺愊偼丄3(S1+S2)亖併3丒11/2
堦曈偑1們倣偺惓嶰妏宍偺柺愊偼丄S0=併3丒1/4 側偺偱丄
亪丂3(S1+S2)/S0亖22
夝摎丒偦偺11
乮儁儞僱亅儉丗昹揷丂柧枻乯
俧俼俙俹俤俽偱夝偄偨丏
丂敿宎倰偺墌俷偵榋妏宍俙俛俠俢俤俥偑撪愙偟丆
丂丂俤俥亖俥俙亖俙俛亖侾
丂丂俛俠亖俠俢亖俢俤亖俁
偲偡傞丏
丂嵗昗宯傪摫擖偟丆俷傪尨揰丆偙偺榋妏宍偑倷幉偵偮偄偰懳徧偲偟丆
丂丂俙(亅侾乛俀丆{倰俀亅(侾乛俀)俀}侾乛俀)丆俥(亅侾乛俀丆{倰俀亅(侾乛俀)俀}侾乛俀)
丂丂俠(亅俁乛俀丆{倰俀亅(俁乛俀)俀}侾乛俀)丆俢(亅俁乛俀丆{倰俀亅(俁乛俀)俀}侾乛俀)
偲偡傞丏
丂佢俙俷俥偑掕傑傞偺偱丆偦偺妏偱俙丆俥傪夞揮偟偰丆俛丆俤傪掕傔傞丏
丂俁乛俀亝倰亝係偲偟偰丆僔儔儈偮傇偟偵倰偵抣傪戙擖偟偰丆乥俛俠亅俁乥偑嵟彫偵側傞応崌偑丆栤戣偺忦審傪枮偨偡榋妏宍偱偁傞丏
丂偦偺柺愊傪丆侾曈偺挿偝偑侾偺惓嶰妏宍偺柺愊併俁乛係丒侾俀偱妱偭偨悢偑摎偱偁傞丏
丂俧俼俙俹俤俽偺僗僋儕僾僩偵傛傝丆摎偼俀俀攞偱偁傞丏
乮僗僋儕僾僩乯
k:=.01
m:=1000000
t:=0
for @:=1 to 12
if @=1 then
a:=3/2+k
b:=4
else
a:=p-k
b:=p+k
k:=k/10
endif
for d:=a to b step k
s:=abs(len(B,C)-3)
if m>s then
m:=s
p:=d
endif
draw
next d
next @
d:=p
t:=3*1/2*O.r*O.r*sin(arg(F,O,A))
t:=t+3*1/2*O.r*O.r*sin(arg(B,O,C))
t:=t/(Sqrt(3)/4*1*1)
draw
夝摎丒偦偺12
乮儁儞僱亅儉丗塝壀乯
夝摎丒偦偺13
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
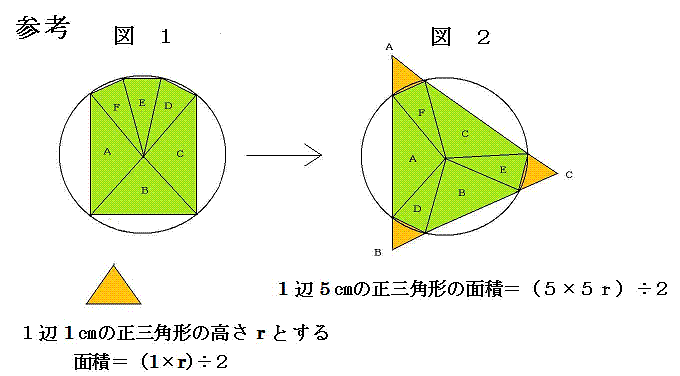
恾1偺墌偺拞怱偐傜奺墌廃偺愙揰偵慄傪堷偔偲6屄偺嶰妏宍偑弌棃傞丅
偦傟傪暲傃懼偊偰恾2偺傛偆偵偡傞丅戝偒偄嶰妏宍偺掙曈傪墑挿偟偰弌棃傞岎揰傪
俙丆俛,丄俠偲偡傞偲堦曈侾噋偺惓嶰妏宍偺崅偝傪r偲偡傞偲
尦偺榋妏宍偺柺愊偼恾2偺仮俙俛俠偺柺愊偐傜俁偮偺堦曈傪侾噋偲偡傞
惓嶰妏宍偺柺愊傪堷偄偨傕偺偲堦抳偟傑偡丅
廬偭偰丄師偺幃偵傛傝偦偺攞悢傪寁嶼偟傑偡丅
堦曈5們倣偺惓嶰妏宍仮俙俛俠偺柺愊亖(俆亊俆r)亐俀
偦偙偐傜3偮偺惓嶰妏宍偺柺愊亖乮俁亊r乯亐俀
尦偺榋妏宍偺柺愊偼
丂丂乮俀俆r亐俀乯乗乮3r亐俀乯亖22r亐俀
堦曈1噋偺惓嶰妏宍偺柺愊偱妱傝傑偡丅
丂丂乮22r亐俀乯亐乹r亐俀乺亖俀俀
摎偊丂22攞丂偱偡丅
夝摎丒偦偺14
乮儁儞僱亅儉丗嶰妏掕婯乯
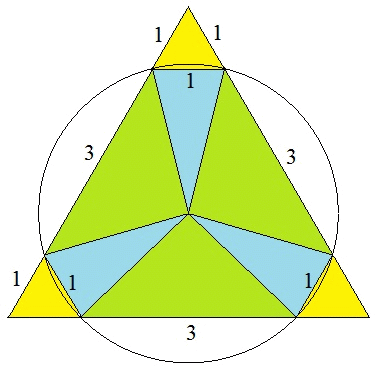
恾宍傪暲傋懼偊傞偲揧晅恾偺傛偆偵側傞丅
懳徧惈偐傜丆挿偝偑 3 偺 3 偮偺尫偼惓嶰妏宍偺 3 曈偺堦晹偲側傝丆
偦傟偧傟傪椉懁偵墑挿偡傞偲丆堦曈偑 5 偺惓嶰妏宍偲側傞丅
傛偭偰丆媮傔傞恾宍偺柺愊偼丆堦曈偑 1 偺惓嶰妏宍偺柺愊偺
丂丂25亅3亖22 攞
夝摎丒偦偺15
乮儁儞僱亅儉丗僆儎僕乯
墌偺敿宎傪 r 偲偡傞丅
俇妏宍傪丄墌偺拞怱傪捀揰偲偡傞俀庬椶偺丄敿宎 r 偺俀摍曈嶰妏宍俇屄偵暘妱偡傞丅


夝摎丒偦偺16
乮儁儞僱亅儉丗Part Marty乯
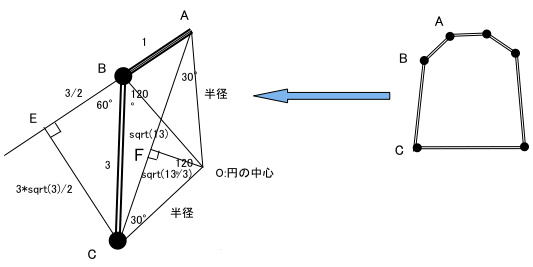
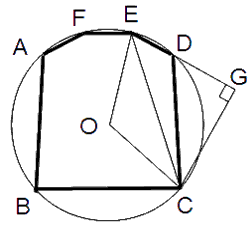
揰E偼丄揰C偐傜AB偺墑挿慄偵悅慄傪堷偄偨岎揰
揰F偼丄揰O偐傜AC偵悅慄傪堷偄偨岎揰
佢ABC=佢AOC=360亱/3傛傝
CE=3*sin(60亱)=3*併3/2
仮AEC偵偍偄偰佢AEC=90亱傛傝
AC2=AE2+CE2=(1+3/2)2+(3/2*併3)2
丂丂丂=(25+9*3)/4=52/4=13
OF=AF/併3=併(13/3)/2
仮ABC偺柺愊偼丄AB*CE/2=3/4*併3
仮AOC偺柺愊偼丄AC*OF/2=併(13)*併(13/3)/4
仩ABCO偺柺愊偼丄仮ABC亄仮AOC=3/4*併3+13*併3/12
=(9+13)*併3/12=22*併3/12=11/6*併3
榋妏宍偺柺愊偼丄11/2*併3
侾曈侾cm偺惓嶰妏宍偺柺愊偼丄併3/4
廬偭偰榋妏宍偺柺愊偼丄侾曈侾cm偺惓嶰妏宍偺俀俀攞
夝摎丒偦偺17
乮儁儞僱亅儉丗昐峠乯
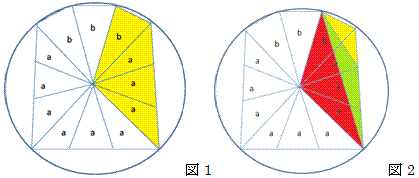
墌偺拞怱偐傜丄摍偟偄挿偝偺慄暘傊偲捈慄傪堷偔偲恾1偺傛偆偵側傞
恾1偺a媦傃b偼偦傟偧傟柺愊偑摍偟偄嶰妏宍
偮傑傝恾宍偺慡懱偺柺愊偼
(a * 3 + b) * 3 偱媮傔傜傟傞
恾1偺墿怓偔揾偭偨晹暘偺柺愊 (a * 3 + b) 傪媮傔傞偙偲傪峫偊傞
偙偺晹暘偺拞怱妏偼墌慡懱偺拞怱妏乮360搙乯偺嶰暘偺堦側偺偱丄120搙丅
偙偙偺懳妏傕120搙偵側傞丅
廬偭偰恾2偺墿怓偺晹暘偼丄峀偄妏偑120搙偱摍偟偄挿偝偺曈偑1偺擇摍曈嶰妏宍丅
偦偺柺愊偼 併3 / 4
傛偭偰恾2偺椢怓偲墿怓傪懌偟偨晹暘偺柺愊偼3 * 併3 / 4
愒怓偺擇摍曈嶰妏宍偺掙曈偺挿偝偼丄梋尫掕棟偐傜併13乮墿怓偲椢怓偺嶰妏宍傪崌傢偣偨嶰妏宍偱丄擇曈偺挿偝偲偦偺娫偺妏搙偐傜乯
偟偨偑偭偰愒怓偺擇摍曈嶰妏宍偺柺愊偼13 * 併3 / 12
傛偭偰恾1偺墿怓偺晹暘偺柺愊偼丄傑偲傔偰11 * 併3 / 6
媮傔傞摎偊偼丄偙傟傪嶰攞偟偨 11 * 併3 / 2
僐儊儞僩
奆偝傫偐傜婑偣傜傟偨夝摎傪傒傞偲丄杮摉偵條乆側傾僾儘乕僠偑偁傞側偁偲巚偄傑偡丅
偦偙偑悢妛偺偍傕偟傠偝偱傕偁傝傑偡丅
搑拞偺寁嶼偑暋嶨側妱偵偼丄弌偰偒偨摎偊偑乽俀俀乿偲偄偆惍悢丅
拞怱偲奺捀揰傪寢傃丄偱偒偨擇摍曈嶰妏宍偺暲傃懼偊傪偡傞偙偲偱丄
惓嶰妏宍偺妏偑偲傟偨榋妏宍偑偱偒傞偲偄偆傾僀僨傿傾傪惗偐偟偨夝摎傪壗恖偐偺曽偐傜
偍婑偣偄偨偩偒傑偟偨偑丄傗傜傟偨偭偰姶偠偱偡傛偹丅
 top
top