問題191　マッチ棒の問題

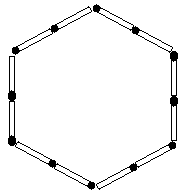
図のように、同じ長さのマッチ棒１２本を１辺に２本ずつ使って正六角形を作りました。これら１２本のマッチ棒のうち、５本だけを動かして、面積が図の正六角形の1/3である多角形になるようにしてください。

問題の出典

パズルより面白い中学入試の算数
ピーター・フランクル
講談社

解答

～到着順にご紹介します～

解答・その1

（ペンネ－ム：次郎長）

マッチ棒3本で出来る正三角形の面積を1とすると、
正六角形の面積は２４。これを８にする。

６つの頂点をＡ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆとし、ＥとＦの中間点をＧとし、
ＣとＧを結んだ直線で区切られた面積はうまい具外に１６と８になる。

ＣＧで点Ｄ，Ｅを含む方をＡ，Ｂ，Ｆを含むほうに折り返せば
１６－８＝８で面積は１／３になります。

触ったマッチ棒は、ＣＤ間の２本、ＤＥ間の２本、ＥＧの1本、合計５本

解答・その2

（ペンネ－ム：haya）

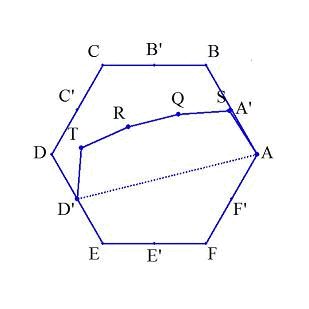
答： image2 の如く内部で左からマッチ棒 2-2-1 本とすると面積が 1/3 となる
【解き方】

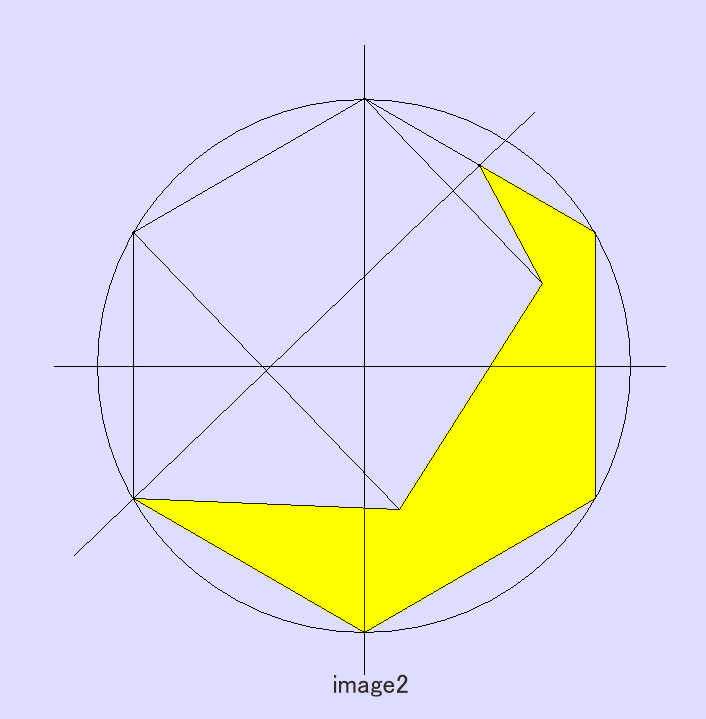
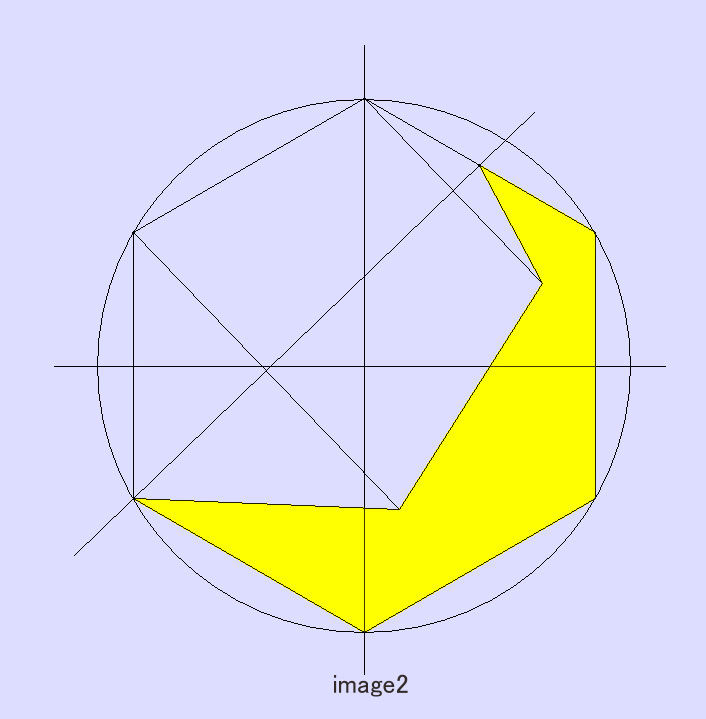
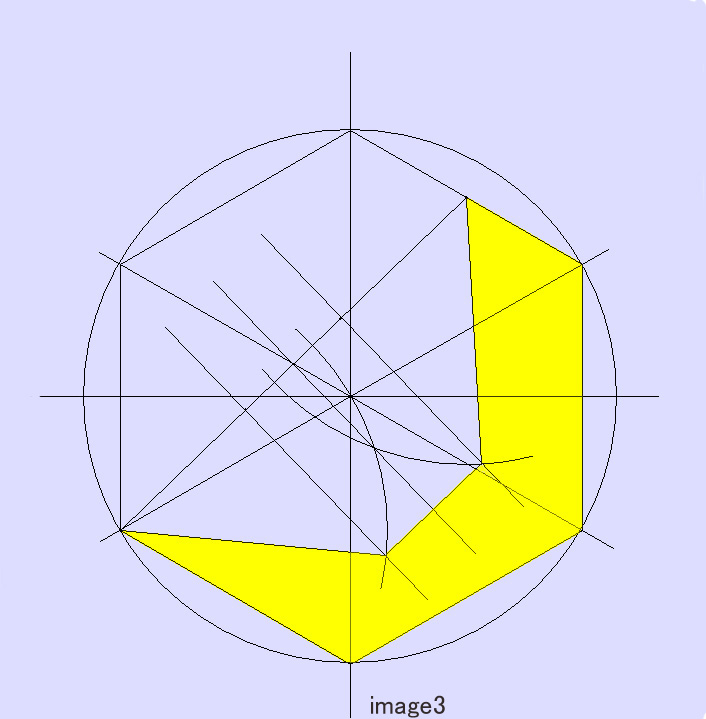
image1 の如く 1-1-1-2 とすると面積は 5/12 となり 1/3 より大。
image2 では
　　正6角形の面積が 6√3
　　消える面積が 2√3 ｘ 2 より、
　　残る面積は 6√3 - 4√3 = 2√3
　　丁度 1/3
image3 のような 2-1-2 は消える面積が image2 より大きいから不適合

解答・その3

（ペンネ－ム：スモークマン）

六角形ABCDEF=24 とすると…
菱形ABCO=4*2=8, △ABC=4
□ABCD=12, △ACG=△ADG=(12-4)/2=4
五角形AGDEF=12+4=16
□ABCG=4+4=8
五角形AGDEF-□ABCG=16-8=8
8=24/3 なので…□ABCGをAGを軸に六角形内部に折り畳めば可能なことがわかる♪

解答・その4

（ペンネ－ム：Ryu1128）

下図のように正六角形を24個の正三角形に分割し、一つの正三角形の面積を1とします。（正六角形の面積は24です）
FからGに補助線を引き線分BEとの交点をOとします。

6角形FJMGDEの面積は16です。
4角形GDEFは4角形FJMGとOについて点対象であり合同です
したがって4角形FJMGの面積は8です。
そこで4角形FJMGを線分FGに対し線対称になるよう折り込みます（下図参照）

7角形ABCGD’E’Fの面積は24-8-8＝8
正六角形の面積は24の1/3になります。
5本のマッチは、GD、DH、HE、EI、IFです。

解答・その5

（ペンネ－ム：のっこん）

正六角形をABCDEF、一辺の長さを2、DEの中点をMとする

正六角形の面積は6√3・・・・・[1]
二等辺三角形ABMの面積は2√3・・・・・[2]
対称性から、四角形AMEFと四角形BCDMの面積は等しい・・・・・[3]

[1]、[2]、[3]より
四角形BCDMの面積は2√3
五角形BMEFAの面積は4√3

よってBMを軸として四角形BCDMを折り返し
Cの移動先をC´、Dの移動先をD´とすると
七角形ABC´D´MEFの面積は
4√3－2√3＝2√3 となる
これは正六角形の面積の1/3である

解答・その6

（ペンネ－ム：夜ふかしのつらいおじさん）

●マッチ棒１本の長さを単位とします。
単位の長さの正三角形が２４個あるので、８個分になることを考えます。

●マッチ棒１本とったとき、多角形を作るために切れ目をつなぐには２本上のマッチ棒を使います。
１本でつなぐとすると元に戻ってしまいます。

とびとびの２ヶ所で２本のマッチ棒を取ることはできません。
２ヶ所の切れ目をつなぐには４本以上のマッチ棒を使いますが、とった２本で１ヶ所はつなげられますが、もう１ヶ所をつなぐために他のところのマッチ棒を取った時点で３ヶ所のマッチ棒を取ることになります。
また、３ヶ所をつなぐためには、６本以上のマッチ棒を使うことになるので、切れ目は１ヶ所だけです。
つまり連続した５本のマッチ棒を使うことになります。

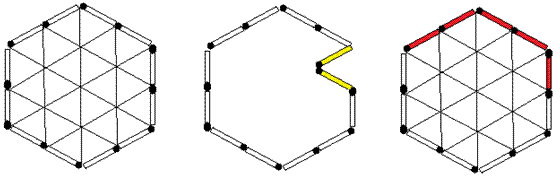
●取った５本のマッチ棒を普通につなぐと、単位の正三角形１０個分になります。
そこで図のように凹ませると単位の正三角形８個分にできます。

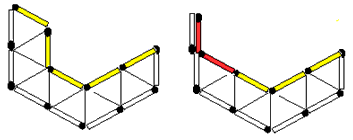
●次に１２本のマッチ棒全体で多角形を作るように等積変形をします。
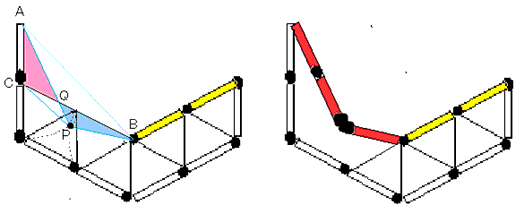
Aを中心に２単位の長さ、Bを中心に１単位の長さで弧をかき、交点をPとします。
△APBと△BCAは、ABが共通で他の二辺がそれぞれ１単位，２単位なので合同です。
すると、△ACQ＝BPQとなります。
以上から次のようになります。

解答・その7

（ペンネ－ム：ちょろんは太太）

下図において、□ABCOの面積は、元の６角形の３分の１
△AOCと△ACDは、面積が同じなので、□ABCOと□ABCDの面積は同じ
従って、□ABCDは、６角形の３分の１の面積になる。

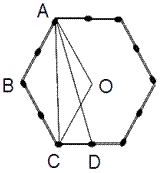
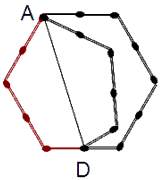
そこで、下図のように、赤に色付けした５本のマッチ棒を直線ADを対称軸として、対称の位置に移動させる。
できた六角形は、もとの六角形の面積の３分の１になり、題意を満足している。

解答・その8

（ペンネ－ム：転位反応）

先ず、隣り合う５本のマッチ棒を動かさないとマッチ棒が不足して多角形を形成できないので、連続した位置にある５本のマッチ棒を動かすことにする。

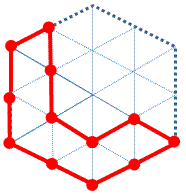
例えば、以下のように５本のマッチ棒を動かすことで多角形を形成できるが要求されている面積よりも大きく、条件を満たさない。
正三角形の格子点にどのようにマッチ棒を配置しても、この図よりも面積を小さくできないので次に、格子点を外してマッチ棒を配置することを考える。

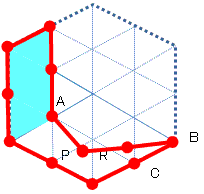
さて、下図において、水色の平行四辺形の部分の面積は正六角形全体の１／６なので、多角形の残りの部分を格子点を外してマッチ棒を配置すると、条件を満たす可能性のある多角形を作成できる。
よって、この部分の面積が正六角形全体の１／６であることを示せば良い。

マッチ棒の長さを1とすると、点Pは点Aを中心とする半径１の円と点Bを中心とする半径2の円の交点である。
∴△APR≡△BCRを示せば良い。ここで点Rを線分ACと線分BPの交点とする。

△ACPと△BPCについて、AP＝BC=1、AC＝BP=2、PC=共通
∴△ACP≡△BPC
∴△APR≡△BCR (∵△PCR=共通)

解答・その9

（ペンネ－ム：浜田　明巳）

正六角形をＡＢＣＤＥＦ，ＡＢ，ＢＣ，ＣＤ，ＤＥ，ＥＦ，ＦＡの中点をＡ'，Ｂ'，Ｃ'，Ｄ'，Ｅ'，Ｆ'，正六角形の１辺の長さを２とする．
　ｘｙ座標を導入し，Ａ(２，０)，Ｂ(２cos(π／３)，２sin(π／３))，Ｃ(２cos(２π／３)，２sin(２π／３))，・・・，Ｆ(２cos(５π／３)，２sin(５π／３))とする．
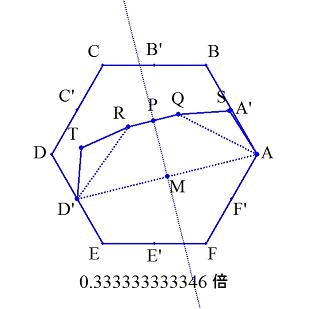
　マッチＤ'Ｅ，ＥＥ'，Ｅ'Ｆ，ＦＦ'，Ｆ'Ａを動かすとする（下図参照）．

　折れ線Ｄ'ＥＥ'ＦＦ'Ａを内側に折り，面積が元の正六角形ＡＢＣＤＥＦの１／３倍になるようにする．
　ＡＤ'の中点をＭ，ＡＤ'の垂直二等分線を引き，その直線上にあり，五角形ＡＢＣＤＤ'の内側に点Ｐをとる．
　簡単の為に，ＰＭに対称的に折れ線をとる．
　Ｐを通る１つのマッチをＱＲとし，折れ線ＡＳＱ，Ｄ'ＴＲをとる．
　シラミつぶしにＰをとり，九角形ＡＢＣＤＤ'ＴＲＱＳの面積を求め，条件に合う場合を求める．
　ＧＲＡＰＥＳを使い，求めると，下図の場合，ほぼ条件に合うものとなる．
　ＧＲＡＰＥＳは近似計算を行っているが，少なくともほぼ１／３の面積となる場合が存在することが分かる．したがって正解の図もほぼこれに近いものとなる．

　具体的な計算方法は以下の通り．
　　－１≦Ｐｘ≦Ｍｘ
　　Ｐｙ＝－(Ａｘ－Ｄ'ｘ)／(Ａｙ－Ｄ'ｙ)×(Ｐｘ－Ｍｘ)＋Ｍｙ
　　Ｑｘ＝Ｐｘ＋１／２×cos(atan((Ａｙ－Ｄ'ｙ)／(Ａｘ－Ｄ'ｘ)))
　　Ｑｙ＝Ｐｙ＋１／２×sin(atan((Ａｙ－Ｄ'ｙ)／(Ａｘ－Ｄ'ｘ)))
　　Ｒｘ＝Ｐｘ＋１／２×cos(atan((Ａｙ－Ｄ'ｙ)／(Ａｘ－Ｄ'ｘ))＋π)
　　Ｒｙ＝Ｐｙ＋１／２×sin(atan((Ａｙ－Ｄ'ｙ)／(Ａｘ－Ｄ'ｘ))＋π)
　　Ｓｘ＝Ｑｘ＋１×cos(acos(ＡＱ／２)＋atan((Ａｙ－Ｑｙ)／(Ａｘ－Ｑｘ)))
　　Ｓｙ＝Ｑｙ＋１×sin(acos(ＡＱ／２)＋atan((Ａｙ－Ｑｙ)／(Ａｘ－Ｑｘ)))
　　Ｔｘ＝Ｄ'ｘ＋１×cos(acos(ＲＤ'／２)＋atan((Ｒｙ－Ｄ'ｙ)／ (Ｒｘ－Ｄ'ｘ)))
　　Ｔｙ＝Ｄ'ｙ＋１×sin(acos(ＲＤ'／２)＋atan((Ｒｙ－Ｄ'ｙ)／(Ｒｘ－Ｄ'ｘ)))
　　ＳがＡＢの下にあるときのみ計算
　　九角形ＡＢＣＤＤ'ＴＲＱＳの面積＝△ＡＢＳ＋△ＣＢＳ＋△ＣＳＱ＋△ＣＱＲ＋△ＣＲＴ＋△ＣＴＤ＋△ＤＴＤ'
　この計算の元で，
　　｜九角形ＡＢＣＤＤ'ＴＲＱＳ／六角形ＡＢＣＤＥＦ－１／３｜が最小になる
場合を求める．

　最後に．算数では，凹多角形の面積は取り扱わないことになっていたのではないでしょうか．ピーター・フランクルさんは知っているのでしょうか．でもピーターさんのことだから，確信犯である可能性は高いですね．正解が凹多角形ではない場合は，こちらが恥をかいてしまいますが．

解答・その10

（ペンネ－ム：Asterisk*）

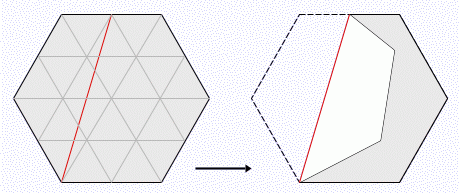
初めのうちは、三角形だけで作ろうとしていたため、うまくいきませんでした。悩んだあげく“折る”ことを思いつき、上記の図の赤色の線の所で折り返してみました。これで、グレーの部分の面積は三角形8個分になり、三角形24個分の 1/3になります。

解答・その11

（ペンネ－ム：まーりんａｎｄさとりん）

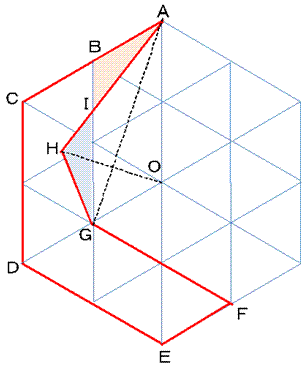
多角形ＢＣＤＥＦＧの面積は六角形の１／３なので、△ＡＢＩ≡△ＧＨＩを示せばよい。
ここで、△ＡＨＯ及び△ＧＨＯは、ともに二等辺三角形なので、△ＡＨＧ≡△ＡＯＧ
よって　∠ＡＢＩ＝∠ＧＨＩ＝１２０°
また、対頂角なので、∠ＢＩＡ＝∠ＨＩＧ
２角が等しいので、∠ＢＡＩ＝∠ＨＧＩ
さらに、辺ＡＢ＝辺ＧＨ＝（まっち棒１本の長さ）なので、
１辺両角が等しい
∴△ＡＢＩ≡△ＧＨＩ

よって、多角形ＡＣＤＥＦＧＨは六角形の面積の１／３であるので、
赤いマッチ棒の位置へ５本動かせばよい。

解答・その12

（ペンネ－ム：三角定規）

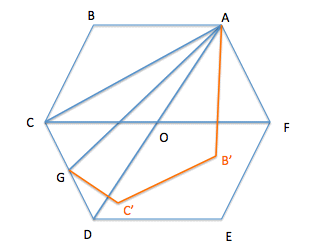
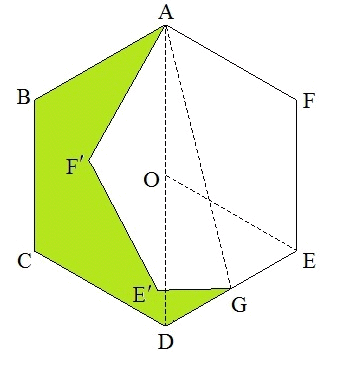
添付図において，ABCDEF を1辺が2の正六角形とする。O はその中心，G は辺DEの中点とする。
1辺が2の正三角形の面積を S とすると，正六角形の面積は 6S。
△ADG は △ODE と比べ，底辺が2倍 (AD＝2OD)，高さが 1/2 だから両者の面積は等しく，△ADG＝S。
よって，四辺形(四角形)AGEF＝2S，五角形ABCDG＝4S。

よって，ABCDEF を AG を折り目にして折り返すと，着色した多角形の面積は 4S－2S＝2S で，ABCDEF 面積の 1/3。
これは，原題でマッチ棒を5本動かすことに相当している。　［了］

解答・その13

（ペンネ－ム：杖のおじさん）

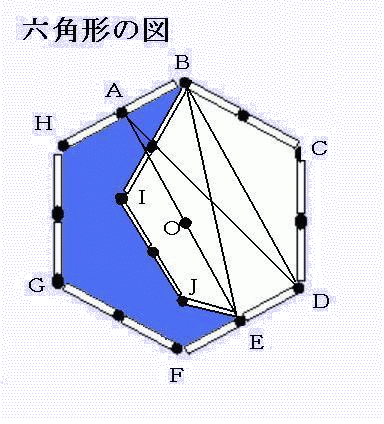
図を参照して下さい。
六角形の面積は△Ｏ（中心点）ＨＧの六倍です。線分ＯＨ＝rとすると
　　（２×r）/2×６＝６r
線分ＡＥを引くと六角形は半分になります。
　　△ＥＤＢ＝（１×２r）/2=r
従って
　　□ＨＢＦＤ＝４r
　　△ＢＣＤは（６r―４r）/２＝ｒ
　　□ＢＣＤＥはｒ＋ｒ＝２ｒ
六角形ＢＣＤＥＪＩは
　　２ｒ×２＝４ｒ
５本のマッチ棒を動かして出来た多角形の面積は
元の六角形からその面積を引き出来た７角形ＢＨＧFEJIの多角形の面積は
　　６r－４r＝２r
で1/３となります。

連続するマッチ棒５本分で、ちょうど全体の面積の1/3になることに気づくと、そこで折り返せばよいことになりますね。

Challenge!