���190�@�����Z�̃s���~�b�h
���̐}�́A 1 ���� 6 �܂ł̐�����ׁA �ׂ荇�������𑫂��A���̘a���Q�̐��̉��L������Ƃ���������������̂ł��B
�@1�@�@2�@�@3�@�@4�@�@5�@�@6 �@�@3�@�@5�@�@7�@�@9�@�@11 �@�@�@8�@�@12�@ 16�@�@20 �@�@�@�@20�@�@28�@ 36 �@�@�@�@�@�@48�@ 64�@ �@�@�@�@�@�@�@112
���̂悤�ɁA�u1�C2�C3�C4�C5�C6�v�ƕ��ׂĎn�߂�ƁA��ԉ��́u112�v�ɂȂ�܂��B
�ł́A 1 ���� 6 �̐��̏��Ԃ����ւ��邱�Ƃɂ���āA���̐����u100�v�ɂȂ���̂������Ă��������B
���̏o�T
�s�[�^�[�E�t�����N���̒��w���ł��������l�������Ȃ����W�@�㐔��
���{�]�_��
��
�`�������ɂ��Љ�܂��`
�E����1
�i�y���l�|���Fhaya�j
���F
�@(a, f) = (4, 6)
�@(b, e) = (1, 3)
�@(c, d) = (2, 5)�@�̑g�����ō��v��100�ƂȂ�B
�܂�A�g�����Ƃ��ẮA
�@4 1 2 5 3 6
�@4 1 5 2 3 6
�@4 3 2 5 1 6
�@4 3 5 2 1 6
�@6 1 2 5 3 4
�@6 1 5 2 3 4
�@6 3 2 5 1 4
�@6 3 5 2 1 4�@��8�ʂ�B
�y�������z
���v�́A
�@�@a + 5b + 10c + 10d + 5e + f = 100
���A
�@�@(a + f) = 5(20 - (b + e) -2(c + d))
��������A
�@�@(a, f) = (1, 4) or (2, 3) or (4, 6)
(a, f) = (4, 6)�@�̎��A
18 = (b + e) + 2(c + d)�@�ƂȂ�A
(b, e) = (1, 3),�@(c, d) = (2, 5) �ʼn������B
(a, f) = (1, 4) or (2, 3)�@�̎��́A
19 = (b + e) + 2(c + d)�@�ƂȂ�A
�c��� 2, 3, 5, 6 ���邢�� 1, 4, 5, 6 ���ǂ̂悤�ɑg�����Ă� 19 �ɂ͂Ȃ�Ȃ��B
�E����2
�i�y���l�|���FT_Tatekawa�j
��ԏォ���ԉ��܂Ői�ލہC��ԏ�̊e�X�̐����u112�v�ɓ��B����o�H��
���ʂ肠�邩���l����D
���̒ʂ�̐�������ԏ�̐����Ɋ|���Z�������̂̑��a��112�ƂȂ�D
1, 6 : 1�ʂ�
2, 5 : 5�ʂ�
3, 4 : 5C2 = 10 �ʂ�
�@�@(1+6) x 1 + (2+5) x 5 + (3+4) x 10 = 112
���āC���̑��a�� 100 �ɂ��鎖���l����D
��ԏ�̒i�̐����̑��a��
�@�@1+2+3+4+5+6=21
�ł����͕ς��Ȃ��D
���[�ɓ��鐔���̘a��5�̔{���łȂ���C���a��100�ɂȂ�Ȃ��D
���̘a�� 5 �̎��́C
�@�@5 x 1 + 13 x 5 + 3 x 10 = 100
�� 100 �ƂȂ邪�C2�̐��̘a�� 13 �ɂȂ���̂��I�ׂȂ��̂Ń_���D
�a��10�̎���
�@�@10 x 1 + 4 x 5 + 7 x 10 = 100
�ŁC���ꂼ�� (4, 6), (1, 3), (2, 5) �Ƃ���������I�ׂ����D
�a�� 15 �̎��́C�ǂ�����Ă����a�� 100 �ɂȂ�Ȃ��D
������
�@�@�u4 1 2 5 3 6�v
���邢�� (4, 6), (1, 3), (2, 5) ���e�X�����\�Ȃ̂ŁC���v8�ʂ肠��D
�u4 1 2 5 3 6�v�u4 1 5 2 3 6�v�u4 3 2 5 1 6�v�u4 3 5 2 1 6�v
�u6 1 2 5 3 4�v�u6 1 5 2 3 4�v�u6 3 2 5 1 4�v�u6 3 5 2 1 4�v
���r������u1�~�ʁC5�~�ʁC10�~��21����100�~�ɂ���g�����́H�v��
�������ł͖������ƍl���C����u���������瓚���ɍs�������₷��
�Ȃ�܂����D
�E����3
�i�y���l�|���F���Y���j
1����6�̐������A�`�C�a�C�b�C�c�C�d�C�e�Ƃ����
2�i�ڂ́A�`�{�a�A�a�{�b�A�b�{�c�A�c�{�d�A�d�{�e
3�i�ڂ́A�`�{�Q�a�{�b�A�a�{�Q�b�{�c�A�b�{�Q�c�{�d�A�c�{�Q�d�{�e
4�i�ڂ́A�`�{�R�a�{�R�b�{�c�A�a�{�R�b�{�R�c�{�d�A�b�{�R�c�{�R�d�{�e
�T�i�ڂ́A�`�{�S�a�{�U�b�{�S�c�{�d�A�a�{�S�b�{�U�c�{�S�d�{�e
�U�i�ڂ́A�`�{�T�a�{�P�O�b�{�P�O�c�{�T�d�{�e�ƂȂ�܂�
�܂�A�`�{�e�{�T�i�a�{�Q�b�{�Q�c�{�d�j���P�O�O�ɂȂ�`�C�a�C�b�C�c�C�d�C�e�����߂�Ηǂ�
�܂�A
[1]�@�`�{�e���T�ŁA�a�{�Q�b�{�Q�c�{�d���P�X��
[2]�@�`�{�e���P�O�A�a�{�Q�b�{�Q�c�{�d���P�W���ƂȂ�
[1]�`�{�e���T�ŁA
�@�@�`�C�e���P�C�S�̎��A�a�C�b�C�c�C�d���Q�C�R�C�T�C�U�ƂȂ邪�A
�@�@�a�{�Q�b�{�Q�c�{�d���i�a�{�b�{�c�{�d�j�{�b�{�c���P�X�ƂȂ�A
�@�@�b�{�c���R�ƂȂ�A�s����
�@�@�`�C�e���Q�C�R�̎��A�a�C�b�C�c�C�d���P�C�S�C�T�C�U�ƂȂ邪
�@�@�������A�c�{�d���R�ƂȂ�A��͂�s����
[2]�`�{�e���P�O�̎��A�܂�A�`�C�e���S�C�U�̎�
�@�@�a�C�b�C�c�C�d���P�C�Q�C�R�C�T�ƂȂ�
�@�@�a�{�Q�b�{�Q�c�{�d���i�a�{�b�{�c�{�d�j�{�b�{�c���P�W
�@�@�܂�A�b�{�c���V
�@�@����́A�b�C�c���Q�C�T�Ŗ�����
�ƌ������́A�i�`�C�e�j���i�S�C�U�j�@�@�i�b�C�c�j���i�Q�C�T�j�@�@�i�a�C�d�j���i�P�C�R�j
�Ȃ�A�ǂ�ł��ǂ��ł��ˁB�e�g�Q�ʂ�A
��������
�@�S�P�Q�T�R�U
�@�S�P�T�Q�R�U
�@�S�R�Q�T�P�U
�@�S�R�T�Q�P�U
�@�U�P�Q�T�R�S
�@�U�P�T�Q�R�S
�@�U�R�Q�T�P�S
�@�U�R�T�Q�P�S
�̂W�ʂ�ł��ˁH
�E����6
�i�y���l�|���F�l�c�@�����j
�@�U�������C���C���C���C���C���i�������j�Ƃ��āC�a�����X�ɋ��߂�ƁC
�@�@���{���C���{���C���{���C���{���C���{��
�@�@���{�Q���{���C���{�Q���{���C���{�Q���{���C���{�Q���{��
�@�@���{�R���{�R���{���C���{�R���{�R���{���C���{�R���{�R���{��
�@�@���{�S���{�U���{�S���{���C���{�S���{�U���{�S���{��
�@�@���{�T���{�P�O���{�P�O���{�T���{��
�ƂȂ�̂ŁC
�@�@���{�T���{�P�O���{�P�O���{�T���{�����P�O�O
�@�@���T(���{�Q���{�Q���{��)���P�O�O�|(���{��)�c�c�c(1)
�@�̂ɂ��{���͂T�̔{���ł���D
�@����������C
�@�@(���C��)��(�P�C�S)�C(�Q�C�R)�C(�S�C�U)
i). (���C��)��(�P�C�S)�̂Ƃ��C(1)����C
�@�@���{�Q���{�Q���{�����P�X
�@�@���Q(���{��)���P�X�|(���{��)�c�c�c(2)
�@�̂ɂ��{���͊�ł���D
�@�@��{���C��}��{�Q�C�R}�C{�Q�C�T}�C{�R�C�U}�C{�T�C�U}
�@�c��̐����l����ƁC
�@�@({���C��}�C{���C��})��({�Q�C�R}�C{�T�C�U})�C({�Q�C�T}�C{�R�C�U})�C({�R�C�U}�C{�Q�C�T})�C({�T�C�U}�C{�Q�C�R})
�@�����̒���(2)�������̂͑��݂��Ȃ��D
ii). (���C��)��(�Q�C�R)�̂Ƃ��Ci)�Ɠ��l�ɁC���{���͊�ƕ�����D
�@�@��{���C��}��{�P�C�S}�C{�P�C�U}�C{�S�C�T}�C{�T�C�U}
�@(2)����C
�@�@({���C��}�C���{��)��({�P�C�S}�C�V)�C({�P�C�U}�C�U)�C({�S�C�T}�C�T)�C({�T�C�U}�C�S)
�@�c��̐����l����ƁC���ׂĖ�������D
iii). (���C��)��(�S�C�U)�̂Ƃ��C(1)����C
�@�@���{�Q���{�Q���{�����P�W
�@�@���Q(���{��)���P�W�|(���{��)�c�c�c(3)
�@�̂ɂ��{���͋����ł���D
�@�@��{���C��}��{�P�C�R}�C{�P�C�T}�C{�R�C�T}
�@�c��̐����l����ƁC
�@�@({���C��}�C{���C��})��({�P�C�R}�C{�Q�C�T})�C({�P�C�T}�C{�Q�C�R})�C({�R�C�T}�C{�P�C�Q})
�@�����̒���(3)�������̂́C
�@�@({���C��}�C{���C��})��({�P�C�R}�C{�Q�C�T})
�@�������̏ꍇ���l����ƁC���߂邁�`���̑g�́C
�@�@({���C��}�C{���C��}�C{���C��})��({�S�C�U}�C{�P�C�R}�C{�Q�C�T})
�@��̓I�ɏ����o���ƁC
�@�@(���C���C���C���C���C��)��
(�S�C�P�C�Q�C�T�C�R�C�U)�C(�S�C�P�C�T�C�Q�C�R�C�U)�C(�S�C�R�C�Q�C�T�C�P�C�U)�C(�S�C�R�C�T�C�Q�C�P�C�U)�C
�@�@�@�@�@�@�@�@�@�@�@�@�@�@
(�U�C�P�C�Q�C�T�C�R�C�S)�C(�U�C�P�C�T�C�Q�C�R�C�S)�C(�U�C�R�C�Q�C�T�C�P�C�S)�C(�U�C�R�C�T�C�Q�C�P�C�S)
�̂W�ʂ�D
�G�N�Z���̃}�N���ŋ��߂�ƁC�ȉ��̒ʂ�ł���D
Option Explicit
'a b c d e f
' a+b b+c c+d d+e e+f
' a+2b+c b+2c+d c+2d+e d+2e+f
' a+3b+3c+d b+3c+3d+e c+3d+3e+f
' a+4b+6c+4d+e b+4c+6d+4e+f
' a+5b+10c+10d+5e+f
Sub Macro1()
Sheets("Sheet1").Select
Dim a As Integer
Dim b As Integer
Dim c As Integer
Dim d As Integer
Dim e As Integer
Dim f As Integer
Cells(1, 1).Value = 0
For a = 1 To 6
For b = 1 To 6
If a <> b Then
For c = 1 To 6
If a <> c And b <> c Then
For d = 1 To 6
If a <> d And b <> d And c <> d Then
For e = 1 To 6
If a <> e And b <> e And c <> e And d <> e Then
f = 1 + 2 + 3 + 4 + 5 + 6 - a - b - c - d - e
If a + 5 * b + 10 * c + 10 * d + 5 * e + f = 100 Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
Cells(Cells(1, 1).Value, 2).Value = a
Cells(Cells(1, 1).Value, 3).Value = b
Cells(Cells(1, 1).Value, 4).Value = c
Cells(Cells(1, 1).Value, 5).Value = d
Cells(Cells(1, 1).Value, 6).Value = e
Cells(Cells(1, 1).Value, 7).Value = f
Range("B" & Cells(1, 1).Value).Select
End If
End If
Next e
End If
Next d
End If
Next c
End If
Next b
Next a
End Sub
�E����7
�i�y���l�|���F�܁[��������Ƃ��j
�����珇�ɂ`�C�a�C�b�C�c�C�d�C�e�@�Ƃ����ƁA�ŏI�i�̐��́A
�@�@�P�O�i�b�{�c�j�{�T�i�a�{�d�j�{�i�`�{�e�j
�ƕ\����B���ꂪ�P�O�O�ɂȂ邽�߂ɂ́A�i�`�{�e�j���T�̔{���ɂȂ�̂�
�i�`�C�e�j�́i�P�C�S�j�i�Q�C�R�j�i�S�C�U�j�̂����ꂩ�ɂȂ�B
�@�i�P�C�S�j���i�Q�C�R�j�̂Ƃ��́A�i�a�{�d�j���
�@�i�S�C�U�j�̂Ƃ��́A�@�@�@�@�@�@�i�a�{�d�j�������@
�̏����ŒT���ƁA
�i�`�C�e�j���i�S�C�U�j�i�a�C�d�j���i�P�C�R�j�i�b�C�c�j���i�Q�C�T�j�łP�O�O�ƂȂ�B
����āA
�`�C�a�C�b�C�c�C�d�C�e��
�@�S�C�P�C�Q�C�T�C�R�C�U
�@�S�C�P�C�T�C�Q�C�R�C�U
�@�S�C�R�C�Q�C�T�C�P�C�U
�@�S�C�R�C�T�C�Q�C�P�C�U
�@�U�C�P�C�Q�C�T�C�R�C�S
�@�U�C�P�C�T�C�Q�C�R�C�S
�@�U�C�R�C�Q�C�T�C�P�C�S
�@�U�C�R�C�T�C�Q�C�P�C�S
�E����8
�i�y���l�|���F�]�ʔ����j
�P����U�܂ł̐���C�ӂɍ����珇��a,b,c,d,e,f�ƒu����
�W������A��ӂ̐��̘a�͎����ŗ^������B
�@�@a+5b+10c+10d+5e+f=100
�������āA
�@�@(a+f)+5(b+e)+10(c+d)=100
���ӂ�10�Ŋ����āA�ȉ��̂悤�ɕό`����B
�@�@(a+f)/10+(b+e)/2+(c+d)=10
�E�ӂ͐����Ȃ̂ŁA
[1](a+f)��10�̔{���ł��邱�Ƃ���Aa+f=10
�@�@��a,f�̉\�ȑg�ݍ��킹�́A(4,6)�̂�
[2](b+e)�͋����ł��邱�Ƃ���Ab+e=4,6,8�܂���10
�@ ����L�@���l������ƁAb,e�̉\�ȑg�ݍ��킹�́A(1,3),(1,5)�A�܂��́A(3,5)
�@ ��b+e=4,6,�܂��́A8
[3]c+d=10-(a+f)/10-(b+e)/2�Ȃ̂ŁA
�@�@b+e=4�̂Ƃ��F�@c+d=10-1-2=7 ��c,d�̉\�ȑg�ݍ��킹�́A2,5�̂�
�@�@b+e=6�̂Ƃ��F�@c+d=10-1-3=6 ��c,d�̉\�ȑg�ݍ��킹�͖���
�@�@b+e=8�̂Ƃ��F�@c+d=10-1-4=5 ��c,d�̉\�ȑg�ݍ��킹�͖���
����āA�e�g�ݍ��킹�́A(a,f)=(4,6), (b,e)=(1,3), (c,d)=(2,5),�Ȃ̂ŁA
���߂鐔�̕��ו��͈ȉ��̂W�ʂ�B
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 4 | 1 | 2 | 5 | 3 | 6 |
| 4 | 1 | 5 | 2 | 3 | 6 |
| 4 | 3 | 2 | 5 | 1 | 6 |
| 4 | 3 | 5 | 2 | 1 | 6 |
| 6 | 1 | 2 | 5 | 3 | 4 |
| 6 | 1 | 5 | 2 | 3 | 4 |
| 6 | 3 | 2 | 5 | 1 | 4 |
| 6 | 3 | 5 | 2 | 1 | 4 |
�E����9
�i�y���l�|���F�I���W�j
�P�ԏ�i���A������E�Ɂ@�`�C�a�C�`�C�e�Ƃ����
�ʼn��i�́A
�@�@�`�{�e�{�T�~�i�a�{�d�j�{�P�O�~�i�b�{�c�j���P�O�O�@�E�E�E�i�P�j
�i�P�j�����@mod�T�ōl�����
�@�@�`�{�e�߂O�@�E�E�E�i�Q�j
�i�Q�j�����@�P�`�U �ōl�����
�@�`�{�e=�P�{�S,�Q�{�R,�S�{�U �̂R���
�]����
�i�T�j�`�{�e���P�{�S�@�̂Ƃ��@�i�P�j���̍ŏ��l�́A
�P�{�S�{�T�~�i�T�{�U�j�{�P�O�~�i�Q�{�R�j���P�P�O�@����Ă`�{�e���P�{�S�́A�s�K
�i�U�j �`�{�e���Q�{�R�@�̂Ƃ��@�i�P�j���̍ŏ��l�́A
�@�Q�{�R�{�T�~�i�T�{�U�j�{�P�O�~�i�P�{�S�j���P�P�O�@����Ă`�{�e���Q�{�R�́A�s�K
�i�R�j�`�{�e���S�{�U�@�̂Ƃ��@�i�P�j���̍ŏ��l�́A
�@�S�{�U�{�T�~�i�T�{�R�j�{�P�O�~�i�P�{�Q�j���W�O���P�O�O
�]���ā@�`�{�e���S�{�U�̂Ƃ��@�̂݁@�\��������
���ہ@�S�{�U�{�T�~�i�P�{�R�j�{�P�O�~�i�Q�{�T�j���P�O�O�@
�o�`�C�e�p���o�S�C�U�p�C�oB�CE�p���o�P�C�R�p�C�oC�CD�p���o�Q�C�T�p�ƂȂ�
����ā@ABCDEF�́A���̂W���
�@�i�A�j �S�P�Q�T�R�U
�@�i�C�j �S�P�T�Q�R�U
�@�i�E�j �S�R�Q�T�P�U
�@�i�G�j �S�R�T�Q�P�U
�@�i�I�j �U�P�Q�T�R�S
�@�i�J�j �U�P�T�Q�R�S
�@�i�L�j �U�R�Q�T�P�S
�@�i�N�j �U�R�T�Q�P�S
�E����10
�i�y���l�|���F�}�V���j
�y�z
������a, b, c, d, e, f�Ƃ���.
a����f�܂ł�1����6�Ȃ̂�,
�@�@a+b+c+d+e+f=21------------(1)
���̌v�Z�̍��v����L�̕������g���ď����\����
�@�@a+5b+10c+10d+5e+f=100
�ƂȂ�.
�@�@a+f+5(b+2c+2d+e)=5*20-----------(2)
�ƍl�����
a+f��5�̔{���ł���
.
���̑g�ݍ��킹��, (2,3), (1,4), (4,6)(���Ԃ̋t���܂߂�)�ł���.
(i) (a,f)=(2,3), (1,4)�̂Ƃ�
(2)��� b+2c+2d+e=19
(1)��� b+c+d+e=16
�����̕ӁX�������� c+d=3
�܂�(c,d)�̑g�ݍ��킹��(1,2)�݂̂ł���.
������, (a,f)�Ŏg�p���Ă��鐔���Əd�������邽�ߕs�K
(ii)(a,f)=(4,6)�̂Ƃ�
��L�Ɠ��l�ɂ���
c+d=7
�܂�(c,d)�̑g�ݍ��킹��(2,5)�݂̂ł���.
�ȏォ��
(a,f)=(4,6), (c,d)=(2,5), (b,e)=(1,3)�̕��ו��ł����, ���v��100�ɂȂ�.
�y�ߒ��z
���̏������𑫂�����1+2,2+3�̌`�ŏ����Ă����Ƃ��ɉ�@���v�����܂���.
�E����11
�i�y���l�|���F�̂�����j
�����珇��a,b,c,d,e,f�ƕ��ׂ��
2�s�ڂ�(a+b),(b+c),(c+d),(d+e),(e+f)
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E
��ԉ���(a+5b+10c+10d+5e+f)
�����10(c+d)+5(b+e)+a+f=100�E�E�E[1]�ƂȂ�悢
�X�I��a��f,b��e,c��d�Ƃ���
�i���P�j
a+b+c+d+e+f=21�c[2]������
[1]�|[2]���9(c+d)+4(b+e)=79�E�E�E[3]�ƂȂ�
2���̘a��3�ȏ�11�ȉ�������
[3]��c+d=7,b+e=4�̎����������
b=1,e=3,c=2,d=5
������a=4,f=6
�����珇��4,1,2,5,3,6�ƕ��ׂ�悢
�i��2�j
[1]���(a+f)��5�̔{���łȂ���Ȃ�Ȃ�
�T�ja=1,f=4�̎��i�c���2,3,5,6�j
�@�@10(c+d)+5(b+e)=95
(b+e)�͊�łȂ���Ȃ�Ȃ�
�@�@�P�jb=2,e=3�̎�10(c+d)=70 �c���5,6������s��
�@�@�Q�jb=2,e=5�̎�10(c+d)=60 �c���3,6������s��
�@�@�R�jb=3,e=6�̎�10(c+d)=50 �c���2,5������s��
�@�@�S�jb=5,e=6�̎�10(c+d)=40 �c���2,3������s��
�U�ja=2,f=3�̎��i�c���1,4,5,6�j
�@�@10(c+d)+5(b+e)=95
(b+e)�͊�łȂ���Ȃ�Ȃ�
�@�@�P�jb=1,e=4�̎�10(c+d)=70 �c���5,6������s��
�@�@�Q�jb=1,e=6�̎�10(c+d)=60 �c���4,5������s��
�@�@�R�jb=4,e=5�̎�10(c+d)=50 �c���1,6������s��
�@�@�S�jb=5,e=6�̎�10(c+d)=40 �c���1,4������s��
�V�ja=4,f=6�̎��i�c���1,2,3,5�j
�@�@10(c+d)+5(b+e)=90
�@�@(b+e)�͋����łȂ���Ȃ�Ȃ�
�@�@�P�jb=1,e=3�̎�10(c+d)=70 �c���2,5�������ӂ���
�@�@�Q�jb=1,e=5�̎�10(c+d)=60 �c���2,3������s��
�@�@�R�jb=3,e=5�̎�10(c+d)=50 �c���1,2������s��
�����珇��4,1,2,5,3,6�ƕ��ׂ�悢
a��f,b��e,c��d�͌����\�Ȃ̂�
2�E2�E2=8�ʂ�̕��ו�������Ǝv���܂�
�E����12
�i�y���l�|���F��ӂ����̂炢��������j
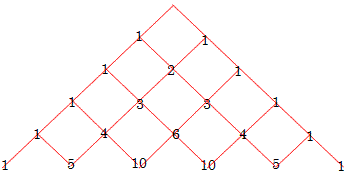 �E�E�}�̂悤�ɁA�p�X�J���̎O�p�`���l���܂��B
�E�E�}�̂悤�ɁA�p�X�J���̎O�p�`���l���܂��B
�O���̍��E�̎߂̂Ƃ����1�ł��B
���ɕ��ԍ��E�̂Q���̘a���������̒i�̐��ł��B
1�b0=1,1�b1=1�Ȃ̂ŁA
n-1�br-1�{n-1�br=n�br�̊W�����Ă͂܂�܂��B
n�͍s���Ar�͍��i�E�j����̏��Ԃ������܂��B
�i�������A�ŏ���0�ł��j
�E���}��a����f��1����6�̐�������U��܂��B
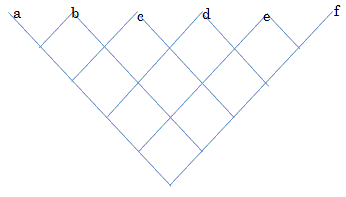
���̂悤�Ȍv�Z������Ԃ��Ƃǂ��Ȃ邩���l���܂��B
�Ⴆ�Ac���ǂ��Ȃ邩��m��ɂ́Ac�̂Ƃ���Ƀp�X�J���̎O�p�`�̒��_���d�˂܂��B
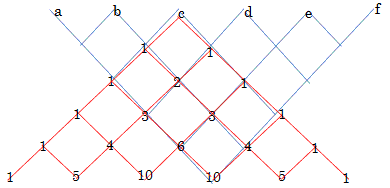
����ƁAc�͑S���łP�O����邱�Ƃ�������܂��B
���̂悤�ɍl���čŏI�I�ɂ́A
�@�@ 1a+5b+10c+10d+5e+1f=1(a+f)+5(b+e)+10(c+d)
�E�����ŁAa+f=X,b+e=Y,c+d=Z �Ƃ����܂��B
a����f�܂ł�1����6�܂ł̂ǂꂩ�Ȃ̂ŁAX�CY�CZ�́A�ŏ���3�A�ő��11�ł��B
�܂��Aa�{b�{c�{d�{e�{f��X�{Y�{Z��21�ł��B
���v��100�ɂȂ�Ƃ��āA���̎��ɂȂ�܂��B
�@�@ X+5Y+10Z=100
��������̂悤�ɕό`���܂��B
�@�@ 5(Y+2Z)=100-X
���̎�����X�́A5��10�ł��B
Y�CZ�ׂ�Ǝ��̂悤�ɂȂ�܂��B
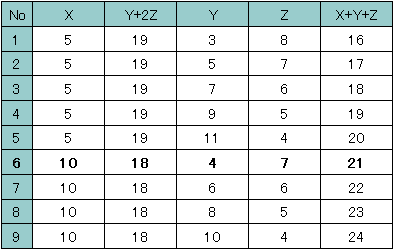
���̂����a��21�ɂȂ�̂́ANo6�̂Ƃ��ł��B
�܂�AX��a�{f��10�AY=b�{e��4�AZ��c�{d��7�ł��B
����āAa��f��4��6�̑g�����Ab��e��1��3�̑g�����ɂȂ�̂ŁAc��d�͎c���2��5�̑g�����ł��B
�E�ȏォ��A�Q3���W�ʂ�̏ꍇ������A���̂悤�ɂȂ�܂��B
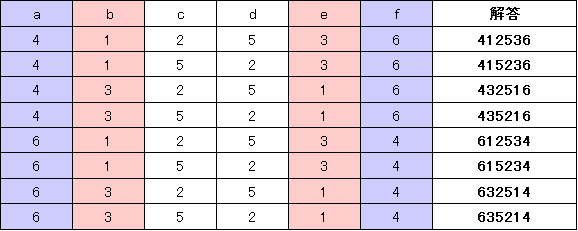
�E����13
�i�y���l�|���F������͑����j
�͂Â��Ōv�Z���܂��B
�P�i�ڂ̐����@a, b, c, d, e, f �Ƃ���ƁA
�Q�i�ڂ̐��́A�@a+b, b+c, c+d, d+e, e+f
�R�i�ڂ̐��́A�@a+2b+c, b+2c+d, c+2d+e, d+2e+f
�S�i�ڂ̐��́A�@a+3b+3c+d, b+3c+3d+e, c+3d+3e+f
�T�i�ڂ̐��́A�@a+4b+6c+4d+e, b+4c+6d+4e+f
�U�i�ڂ̐��́A�@a+5b+10c+10d+5e+f
�������A
�@�@
�@�@a+5b+10c+10d+5e+f = 100
�@�@ (a+f) + 5{b+e+2(c+d)}=100
�E�ӂ́A�T�̔{��������Aa+f ���T�̔{���łȂ���Ȃ�Ȃ��B
�P�`�U�̐��̑g�ݍ��킹�ŁA�����Ȃ�̂́A�P�ƂS�A2��3�A4��6�@�ł���B
a �� f ���A1�� 4�A2�� 3�̏ꍇ�A a + f = 5�@
�@�@5 {b+e+c+d +(c+d)} = 95
�@�@b+e+c+d = (1+2+3+4+5+6)�|(a+f)=16
�@�@c+d = 19 ? 15 = 3
�����āA3 �ɂȂ�g�ݍ��킹�́Ac �� d���A�P �� 2�ł��邪�A
a�Af ���u1�� 4�v�ł��u2�� 3�v�ł��A�g���Ă���̂ŁA�s�K�B
a �� f ���A4�� 6�̏ꍇ�A a + f = 10
�@
�@�@5 {b+e+c+d +(c+d)} = 90
�@�@b+e+c+d = (1+2+3+4+5+6)-(a+f)=11
�@�@c+d = 18 �|11 = 7
�@�@b+e = 11 ? 7 = 4
��������� c �� d �́A2 �� 5�Ab �� e�́A1 �� 3
�܂Ƃ߂��
�@�@a=4�A b=1�A c=2�A d=5�A e=3�A f=6
�@�ia �� f�Ab �� e�Ac �� d �́A�����\�j
�E����14
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�P�{�Q�{�R�{�S�{�T�{�U���Q�P
��i�ځ@�@�`�{�a�{�b�{�c�{�d�{�e���Q�P
��i�ځ@�`�{�a�@�a�{�b�@�b�{�c�@�c�{�d�@�d�{�e
�O�i�ځ@�`�{�Q�a�{�b�@�a�{�Q�b�{�c�@�b�{�Q�c�{�d�@�c�{�Q�d�{�e
�l�i�ځ@�`�{�R�a�{�R�b�{�c�@�a�{�R�b�{�R�c�{�d�@�b�{�R�c�{�R�d�{�e
�ܒi�ځ@�`�{�S�a�{�U�b�{�S�c�{�d�@�a�{�S�b�{�U�c�{�S�d�{�e
�Z�i�ڂ́@�`�{�T�a�{�P�O�b�{�P�O�c�{�T�d�{�e���P�O�O
�Z�i�ڂ����i�ڂ������܂�
�S�a�{�X�b�{�X�c�{�S�d���V�X
�S�i�a�{�d�j�{�X�i�b�{�c�j���V�X
�a�{�d���V�X�|�X�i�b�{�c�j�^�S
�a�{�d�������ɂȂ�b�{�c�������܂��B
�b�{�c�͂R����P�P�܂ł̐����ɂȂ�܂��B
�b�{�c���R�Ƃ���Ƃa�{�d���i�V�X�|�X�~�R�j�^�S���T�R�^�S���P�R�D�Q�T�Ő����łȂ�
�b�{�c���S�Ƃ���Ƃa�{�d���i�V�X�|�X�~�S�j�^�S���S�R�^�S���P�O�D�V�T�Ő����łȂ�
�b�{�c���T�Ƃ���Ƃa�{�d���i�V�X�|�X�~�T�j�^�S���R�S�^�S���W�D�T�Ő����łȂ�
�b�{�c���U�Ƃ���Ƃa�{�d���i�V�X�|�X�~�U�j�^�S���Q�T�^�S���U�D�Q�T�Ő����łȂ�
�b�{�c��7�Ƃ���Ƃa�{�d���i�V�X�|�X�~7�j�^�S���P�U�^�S���S�Ő����ł���B
�]���āA�b�{�c���V�ƂȂ�g������T���a�{�d���S�ƂȂ�
�g������T���܂��B
�a�Ƃd�̑g�����S�͂P�ƂR��������܂���
�b�Ƃc�̑g�����V�͂P�ƂR�������������̑g�ݍ��킹�ƂȂ�܂��B�Q�ƂT�ƂȂ�܂��B
�c�葦���`�Ƃe�͂S�ƂU�ƂȂ�܂��B
�]���āA
�S�C�P�C�Q�C�T�C�R�C�U�ƂȂ�܂��B
���D�a�D�b�D�c�D�d, �e
��i�ځ@�@�S�C�P�C�Q�C�T�C�R�C�U
��i�ځ@�@�@�T�D�R�D�V�D�W�D�X
�O�i�ځ@�@�@ �W.�P�O.�P�T.�P�V
�l�i�ځ@�@�@ �P�W�D�Q�T�D�R�Q
�ܒi�ځ@�@�@�@�@�S�R�D�T�V
�Z�i�ځ@�@�@�@�@�@�P�O�O
�`�Ƃd�A�a�Ƃc�A�b�Ƃc�̐����̏��Ԃ͂ǂ���ɕ��ׂĂ��������ʂɂȂ�܂��B
�Ⴆ��
��i�ځ@�U�{�R�{�T�{�Q�{�P�{�S
��i�ځ@�@�X�{�W�{�V�{�R�{�T
�O�i�ځ@�@�P�V�{�P�T�{�P�O�{�W
�l�i�ځ@�@�@�R�Q�{�Q�T�{�P�W
�ܒi�ځ@�@�@�@�T�V�{�S�R
�Z�i�ځ@�@�@�@�@�P�O�O
���̑��A���ו��͂Q�~�Q�~�Q���W�ʂ肠��܂��B
�E����15
�i�y���l�|���FTeki�j
�W�ʂ蓚��������܂����A���������ƁA������S�P�Q�T�R�U�i�S�ƂU�A�P�ƂR�A�Q�ƂT�͌����\�j
����@��
�@�ȑO�ɂ������s���~�b�h�̖�蓯�l�A�p�X�J���̎O�p�`�𗘗p���܂����B
�@������������a,b,c,d,e,f�Ƃ���ƁA
�U�i�ځi�ʼn��i�j�́A10�~�ic+d�j�{�T�~�ib+e�j�{a�{f�@�ƂȂ�܂��B
�@���ꂪ�P�O�O�ƂȂ�����̂ł����A�P�O�O�͂T�̔{���Ȃ̂ŁAa�{f�@���T�̔{��
�ł���K�v������܂��B
�@�P�`�U�̐��łQ�����ĂT�̔{���ƂȂ�̂́A�P�ƂS�A�Q�ƂR�A�S�ƂU�̂R��ނ݂̂ł��B
�@�P�ƂS�A�Q�ƂR�̏ꍇ�́A10�~�ic+d�j�{�T�~�ib+e�j�͍ŏ��ł��P�O�T�ƂȂ�s�K�B
�@����āA�ia�Cf�j���i�S�C�U�j�i�U�C�S�j�A�܂��Ab+e�͋����ł��邱�Ƃ��킩��܂��B
�@�����܂ł킩��A���Ƃ͎��s����łł��܂��ˁB
�E����16
�i�y���l�|���F�Y���j


�E����17
�i�y���l�|���Ft.a.�j
�ŏ�i��a,b,c,d,e,f�̏��ɕ��ׂ�ƁA
��ԉ���(a+f)+5(b+e)+10(c+d)=100��B
a+f��5�̔{���Ȃ̂ŗႦ��(a,f)=(4,6)�Ǝ���B
���̂Ƃ�b+e�͋����Ȃ̂�b,e��2�ł͂Ȃ��B
��ԉ���100�ɂȂ�g�ݍ��킹�Ƃ��ėႦ��
(a,f)=(4,6)�A(b,e)=(1,3)�A(c,d)=(2,5)������B
�E����18
�i�y���l�|���F�������j
�P�`�U��abcdef�ƑΉ������邱�Ƃɂ��Ĉ�ԉ����v�Z����B
a+5b+10c+10d+5e+f =100�ƂȂ邽�߂ɂ�a+f��5�̔{���łȂ��Ƃ����Ȃ��̂�
(a,f)�̑g�ݍ��킹��(1,4)(2,3)(4,6)�ƂȂ�B
(a,f)��(4,6)�̏ꍇ�ɂ�b+2c+2d+e=18�Ȃ̂�(b,e)�̑g�ݍ��킹��(1,3)(1,5)(3,5)�ƂȂ�B
���̎�c,d�����݂���̂�(b,e)��(1,3)�̎��݂̂�(c,d)��(2,5)�Ƃ�����B
�����菇��(a,f)��(1,4)(2,3)�̏ꍇ�ׂ��(b,e)�̑g�͑��݂��邪
����ɑΉ�����(c,d)�͑��݂��Ȃ��Ƃ킩��B
�ȏォ���ӂ����̂�
�@�@412536,415236,432516,435216
�@�@612534,615234,632514,635214
�̌v�W�ł���
�E����19
�i�y���l�|���FSOU�j
�@�匳�̐��� �@A1 , A2,�E�E�E,AN �@�Ƃ������A�s���~�b�h��ɑ����ē�����ŏI�I�Ȓl�́A �@N-1C0A1 , N-1C1A2 ,�E�E�E, N-1CN-1AN �@�̂悤�ɕ\�����B����͌��̐��� �@A1 , A2,�E�E�E,A6�iA�͂��ꂼ��1�`6�̂��Âꂩ�j �@�Ƃ��Ă���̂ŁA�ŏI�I�Ȓl�́A �@A1 + 5A2 + 10A3 + 10A4 + 5A5 + A6�E�E�E�� �@�ƂȂ�B���ꂪ100�ɂȂ�悢�̂ŁA �@A1 + 5A2 + 10A3 + 10A4 + 5A5 + A6 = 100 �@���������ƂɂȂ�B �@A1 + A6 = 5(20 - A2 - 2A3 - 2A4 - A5) �@�Ƃ���AA1 + A6 ��5�̔{���ɂȂ�˂Ȃ�Ȃ��B�]����(A1,A6) �̑g�ݍ��킹�� �@(A1,A6) = (1,4),(2,3),(3,2),(4,1),(4,6),(6,4) �@�Ɍ�����B �@�������n�߂�4�̑g�ݍ��킹�͂ǂ�Ȃɏ��������ς����Ă� �@�i�W���̑傫�ȂƂ���ɉ\�Ȍ��菬���Ȓl�����蓖�ĂĂ��j �@���ʂ̒l��100���Ă��܂��B �@���̈�(4,6),(6,4)�̑g�ݍ��킹�ɂ��Ă̂ݍl����B���̎����� �@10 + 5A2 + 10A3 + 10A4 + 5A5 = 100 �@�ƂȂ�B����� �@A2 + A5 = 2(9 - A3 + A4) �@�̂悤�ɂ���AA2 + A5 �͋����Ɍ�����B �@�]���� A2 + A5 �̑g�ݍ��킹�� �@(A2,A5) = (1,3),(3,1),(1,5),(5,1),(3,5),(5,3) �@�̂��Âꂩ�ƂȂ邪�͂��߂�2�� �@4 = 2( 9 - 7 ) �@�ƂȂ萳���ő��͕����������Ȃ��B���� �@(A1,A6) = (4,6)or(6,4) �@(A2,A5) = (1,3)or(3,1) �@(A3,A4) = (2,5)or(5,2) �@�̌v8�p�^�[�������̏��������g�ݍ��킹�ƂȂ�B
�E����20
�i�y���l�|���F���q�̗Y�L�j
�@O�@P�@Q�@R�@S�@T �@�@J�@K�@L�@M�@N �@�@�@F�@G�@H�@I �@�@�@�@C�@D�@E �@�@�@�@�@A�@B �@�@�@�@�@100��L�̂Ƃ���A����������ꏊ�ɋL����t����B
���v��100�Ɣ����Ă���̂����牺���珇�Ɍv�Z����ƁA
100=A+B=C+2D+E=F+3G+3H+I=J+4K+6L+4M+N=O+5P+10Q+10R+5S+T
��������(O+T)+5(P+S)+10(Q+R)
�����O+T��5��10�ł���K�v������B
�i�Ȃ��Ȃ�100��5�Ŋ����邩��A
O+T��5��10�łȂ�����v��5�̔{���ɂȂ�Ȃ��j
1)�@O+T��5�̂Ƃ�
���v���ł��������Ȃ�̂��AP+S=6+5=11,Q+R=5�̎������A
���̏ꍇ�A���v��(O+T)+5(P+S)+10(Q+R)=5+55+50=110 �ɂȂ�B
����č��v��100�ɂ͂Ȃ�Ȃ��B
2)�@O+T��10�̂Ƃ�
(O+T)+(P+S)+(Q+R)=1+2+3+4+5+6=21 �Ȃ̂ŁA(P+S)+(Q+R)=11
(O+T)+10(P+S)+10(Q+R)=10+110=120 �Ȃ̂�
(O+T)+5(P+S)+10(Q+R)=100 �ɂȂ邽�߂ɂ�
�i2���̍�����j5(P+S)��20�łȂ���Ȃ�Ȃ��B
�܂�(P+S)��4�łȂ���Ȃ�Ȃ��B
���̏ꍇ�A���v��(O+T)+5(P+S)+10(Q+R)=10+20+70=100 �ɂȂ�B
����čŏ�i�͊O��(O,T)���i4,6�j�@����(P,S)���i1,3�j ����(Q,R)�� (2,5)�@
�i���ꂼ�ꏇ�s���j
���Ƃ��č�����4,1,2,5,3,6
�E����21
�i�y���l�|���FYou�j
����2�̏ꍇ
�@�@�@a b
�@�@�@ c = a+b
����3�̏ꍇ
�@�@�@a b c
�@�@�@d e
�@�@�@ f
����2�̏ꍇ��p����d��e�̉�������
f= d+ e�ɑ�������
�@�@f= a+2b+c
�ƂȂ�
�����6�̐�(a�`f)�܂ł����Ȃ��ƃs���~�b�h�̖��[�̉���A�Ƃ�����
A=a+5b+10c+10d+5e+f�ƂȂ�
A=100����
(a,f)�̍��v�͂T�̔{���ƂȂ�̂�
(a,f)=(1,4)(2,3)(6,4)�@a��f�͌����@�������藧��
(a,f)=(1,4)(2,3)�̏ꍇ (a,f)=(6,4)�̏ꍇ
(b,e)�̍��v�͊�@�@�@�@�@�@�@�@�@(b,e)�̍��v�͋���
(c,d)�͎c��̐�
����āA���̕\�P�̒ʂ�ƂȂ�
�\�P�@�U�̘a�̃s���~�b�h
| (a,f) | �@�@(1,4) | �@�@(2,3) | �@�@(6,4) |
|---|---|---|---|
| (b,e) | �@�@(2,3)(2,5)(3,6)(5,6) | �@�@(1,4)(1,6)(4,5)(5,6) | �@�@(1,3)(1,5) |
| (c,d) | �@�@(5,6)(3,6)(2,5)(2,3) | �@�@(5,6)(4,5)(1,6)(1,4) | �@�@(2,5)(2,3) |
| A | �@�@140 130 120 110 | �@�@140 130 120 110 | �@�@100 90 |
�\�P����䂦��
�@�@(a,f)=(6,4)
�@�@(b,e)=(1,3)
�@�@(c,d)=(2,5)�̑g�ݍ��킹�ł���
�E����22
�i�y���l�|���F�X���[�N�}���j
abcdef �ƒu���čŌ�̐���\����...
�@a+5b+10c+10d+5e+f=100
�@a+f=100-5(b+e+2(c+d))
�@a+f=5, 10
�@a+f=1+4=2+3
�@a+f=4+6
100-(1+4)=95...95/5=19��1...�c��...2,3,5,6=-1,0,-1,0 ��...b+e+2(c+d)��1
����...x
100-(2+3)��1...�c��...1,4,5,6=1,1,-1,0 ��...b+e+2(c+d)��1
1+0+2(1-1)...1+6+2(4+5)=25...x, 4+6+2(1+5)=22...x
100-(4+6)=90...90/5=18��0...�c��...1,2,3,5=1,-1,0,-1 ��...b+e+2(c+d)��0
-1-1+2*(0+1)...2+5+2(1+3)=15...x, 1+0+2(-1-1)...1+3+2(2+5)=18 �r���S��
�������傭...(a,f)=(4,6),(6,4), (b,e)=(1,3),(3,1), (c,d)=(2,5),(5,2)
�@412536
�@415236
�@432516
�@435216
�Ƃ��̋t����
�@635214
�@632514
�@615234
�@612534
��8���
�E����23
�i�y���l�|���F�O�p��K�j
6 �̐� A�CB�CC�CD�CE�CF �����ӂ̂悤�Șa S �����ƁCS��A�{5B�{10C�{10D�{5E�{F�B
A�`F �� 1�`6�CS��100 �̂Ƃ��CS�C5B�{10C�{10D�{5E �� 5 �̔{��������CA�{F �� 5 �̔{���B
����āC(A�CF) �́C(1�C4)�C(2�C3)�C(4�C6)�B
(A�CF) ���C(1�C4)�C(2�C3) �̂Ƃ��C��ӂ��� B�`E �͑��݂��Ȃ��B
(A�CF) �� (4�C6) �̂Ƃ��C(B�CE)��(1�C3)�C(C�CD)��(2�C5) ����ӂ����B
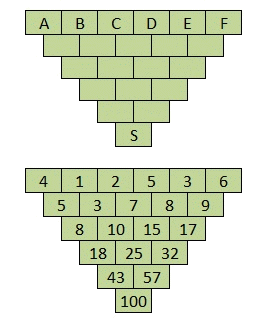
�R�����g
�����̕��̉ɂ���悤�ɁA�ŏ��̐����A���A���A���A���A���A���Ƃ���ƁA
�@�@���{�T���{�P�O���{�P�O���{�T���{�����P�O�O
�Ƃ������������A����ɂ����炆�́A�P�`�U�̐����ł���A
�@�@���{���{���{���{���{�����Q�P
����A
�@�@�S���{�X���{�X���{�S�����V�X
�ƂȂ�܂��B�d�˂āA�����炆�́A�P�`�U�̐����ł��邱�Ƃ���i�荞�ނ��Ƃ��ł��܂��B
�Ώ̐������邱�Ƃ���A���́A���ʂ肩�łĂ���\��������܂��ˁB
�lj��̖��ł��B
����́A��ԉ��̐����u�P�O�O�v�ɂȂ���̂������Ă��炢�܂����B
�ł́A��ԉ��ɂ���\�������鐔���A���ׂĂ����Ă݂Ă��������B
 top
top