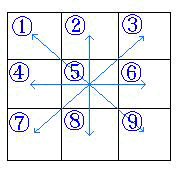
- 儔僢僉亅俈偺栤戣
夞摎丒偦偺侾
乮儁儞僱亅儉丗Kiyokawa乯
A偺儅僗傪倶丄俧偺儅僗傪倷偲偡傞丅嬻敀偺儅僗傪杽傔偰偄偒傑偡丅
倷亖倶亄俀丂偺娭學偑尒偮偐傝傑偡丅倷傪戙擖偡傞偲丄
丂倶丂丂丂丂丂俆俀侾亅倶丂丂俀俆俇
俀俆俈丂丂丂丂倶亄侾丂丂丂俆侾俋亅倶
俆俀侽亅倶丂丂俀俆俆丂丂丂倶亄俀
俥偺儅僗偑俀俆俆偲妋掕偟傑偡丅
俀俆俆丆俀俆俇丆俀俆俈偼巊梡嵪傒側偺偱倶亖俀俆俉偲偡傞丅
丂丂
俀俆俉丂俀俇俁丂俀俆俇
俀俆俈丂俀俆俋丂俀俇侾
俀俇俀丂俀俆俆丂俀俇侽
忋婰偺傛偆偵側傝傑偡丅
夞摎丒偦偺俀
乮儁儞僱亅儉丗Hungry Bear乯
杺曽恮偺朄懃乮儅僗偑婏悢偺帪丠乯
奜榞偺恀傫拞偐傜僗僞乕僩偟丄幬傔壓乮枖偼忋乯偵楢懕偟偨悢帤
乮乽帺慠悢乿偱偄偄傫偱偡傛偹乯傪杽傔偰偄偔丄
婛偵悢帤偑杽傑偭偰偄傞応崌偼偦偺儅僗偺堦偮忋乮壓乯偵擖傟偰偄偔丅
儅僗偺抂偵偒偨傜斀懳懁偺曈偵栠傞丏丏
暥復偱彂偔偲夝傜側偔側傝傑偡偑丄
埲忋偺偙偲偐傜栤戣偺丂俀俆俇丏俀俆俈偼
嵍忋偐傜塃壓偵岦偐偭偰偄傞偺偑夝傝傑偡丅
偦偙偱俙丄俠丄俧偑楢懕偟偨悢帤偱崌寁偑俈俈俈偲尵偆偙偲偵側傝傑偡丅
俈俈俈乛俁亖俀俆俋傛傝丂俙亖俀俆俉丏俠亖俀俆俋丏俧亖俀俇侽
偁偲偼弴斣偵寁嶼偡傞偲慡晹杽傑傝傑偡
俛亖俀俇俁丏俢亖俀俇侾丏俤亖俀俇俀丏俥亖俀俆俆
僐儊儞僩
俈俈俈乛俁亖俀俆俋傛傝丄偳恀傫拞偵擖傞悢帤偑俀俆俋偲傢偐傝傑偡丅
偙傟偑侾儢強傢偐傞偲丄偁偲偼師乆偵寁嶼偡傞偙偲偑偱偒傑偡丅
偱偼側偤丄偳恀傫拞偑暯嬒抣偵側傞偺偱偟傚偆偐丠
忋偺恾偱栴報偵増偭偰丄懌偟嶼傪偟偰偄偒傑偡丅
嘆亄嘍亄嘓亖俈俈俈
嘇亄嘍亄嘒亖俈俈俈
嘊亄嘍亄嘑亖俈俈俈
嘋亄嘍亄嘐亖俈俈俈
偙傟傜丄摍崋偺嵍塃傪偦傟偧傟懌偡偲丄
嘆亄嘇亄嘊亄嘋亄嘍亄嘐亄嘑亄嘒亄嘓亄俁亊嘍亖俈俈俈亊係
偨偩偟丄
嘆亄嘇亄嘊亄嘋亄嘍亄嘐亄嘑亄嘒亄嘓亖俈俈俈亊俁
側偺偱丄
俁亊嘍亖俈俈俈
丂嘍亖俈俈俈乛俁亖俀俆俋
偲偄偆傢偗偱偡丅
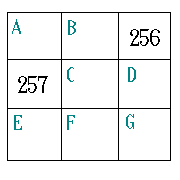
- 崌寁俁係偺栤戣
夞摎丒偦偺侾
乮儁儞僱亅儉丗Kiyokawa乯
E偺儅僗傪倶丄I偺儅僗傪倷偲偡傞丅
侾偺栤戣偲摨條偵嬻敀偺儅僗傪杽傔偰偄偒傑偡丅
C....12-x, E...x, I...y, J...9-y
C+E=9+3=3+9, I+J=5+4=4+5
(C,E,I,J)=(9,3,5,4)丂丒丒丒嘆
=(9,3,4,5)丂丒丒丒嘇
=(3,9,5,4)丂丒丒丒嘊
=(3,9,4,5)丂丒丒丒嘋
偺係捠傝偵峣傜傟傞丅偙偺拞偱丄嘆偺応崌偑壜擻偱偡丅
丂丂侾丂侾侽丂侾俆丂丂俉
丂丂俈丂侾俇丂丂俋丂丂俀
丂侾俀丂丂俁丂丂俇丂侾俁
丂侾係丂丂俆丂丂係丂侾侾
丂忋婰偺傛偆偵側傝傑偡丅丂丂丂丂
夞摎丒偦偺俀
乮儁儞僱亅儉丗akihiro乯
傑偢偙偺栤戣偼A偲H偐傜峫偊傑偟偨丅
偡傞偲丄俁係偐傜堷偒嶼偟偰峫偊傟偽傛偄偺偱偡偐傜丄
A=俉丄H=侾係偲偄偆偙偲偑偡傫側傝傢偐傝傑偟偨丅
偦偟偰崱搙偼丄
D亄G亖侾俆丄I亄J亖俋丄B亄F亖俀俀丄C亄E亖侾俀偲偄偆幃傪敪尒偟丄
偦偺慻傒崌傢偣偼
D亄G亖俀丆侾俁傕偟偔偼俇丆俋
I亄J亖俁丆俇傕偟偔偼係丆俆
B亄F亖侾俇丆俇傕偟偔偼俋丆侾俁
C亄E亖俁丆俋傕偟偔偼係丆俉
偟偐側偄偙偲偑敾柧偟傑偟偨丅
偦偙偱嵟傕戝偒偄悢帤偺侾俇偺張抲傪峫偊偰傒傑偡偲丄
B傕偟偔偼F偵偟偐巊梡偟側偄偙偲偑傢偐傝傑偟偨丅
F偺廲楍偵偼婛偵侾俆偲偄偆悢帤偑巊傢傟偰偍傝丄
侾俆亄侾俇亖俁侾丄偮傑傝巆傝俀儅僗偱俁係亅俁侾偺俁傪
昞尰偱偒側偗傟偽側傜側偄偙偲偵側傝傑偡丅
侾偼婛偵嵍忋偵巊梡偝傟偰偄傑偡偐傜丄
昁慠揑偵侾俇偼B偱偁傝丄F偼俇偱偁傞偙偲偑傢偐傝傑偡丅
偙偺傛偆偵峫偊偰偄偒傑偡偲丄夝偔偙偲偑偱偒傞偲巚偄傑偡丅
傑偲傔傑偡偲丄師偺傛偆偵側傞偺偱偼側偄偱偟傚偆偐丅
A亖俉丄B亖侾俇丄C亖俋丄D亖俀丄E亖俁丄F亖俇丄G亖侾俁丄H亖侾係丄I亖俆丄J亖係
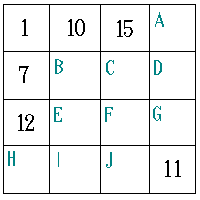
夞摎丒偦偺俁
乮儁儞僱亅儉丗Hungry Bear乯
崱搙偼嬼悢偺帪偺朄懃乮係偺攞悢偺帪丄嬼悢偱係偺攞悢偱側偄偲偒丄偱偦傟偧傟
曽朄偑堘偆傛偆偱偡偑乯偵傛傞偲
侾偲俀丄俁偲係丄俆偲俇丄偺儁傾乕偼僥儗價斣慻乮嶰巬偺怴崶偝傫偄傜偭偟傖偄乯
偺儁傾儅僢僠偺傛偆側暲傃偵側偭偰偄傑偡丅
俙亖俉丂丂俛亖侾俇丂丂俠亖俋丂丂丂俢亖俀丂丂俤亖俁
俥亖俇丂丂俧亖侾俁丂丂俫亖侾係丂丂俬亖俆丂丂俰亖係
僐儊儞僩
乮儁儞僱亅儉丗悈偺棳傟乯
偝偰丄崱寧偺栤戣偱杺曽恮偱偡偑丄巹偑抦偭偰偄傞偲偙傠傪偄偄傑偡丅
僐儊儞僩
側偤丄崌寁偑俁係偵側傞偐丄傢偐傝傑偡偐丠
搊応偡傞悢帤偺憤榓傪媮傔傑偡丅
偦傟傪丄廲係楍暘乮傛偙係楍偱傕傛偄丅乯偲峫偊偰丄係偱妱傟偽偄偄傢偗偱偡丅
乷侾亄俀亄俁亄係亄丒丒丒侾俇乸乛係亖乷乮侾亄侾俇乯亊侾俇乛俀乸乛係
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖侾俈亊俉乛係
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖侾俈亊俀
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俁係
堦斒偵値亊値偺杺曽恮乮値偑俁埲忋偺帪偼嶌傞偙偲偑偱偒傑偡丅乯偱偼丄
侾偐傜値俀傑偱偺憤榓傪値偱妱傟偽偄偄傢偗偱偡偐傜
乷侾亄俀亄俁亄係亄丒丒丒値俀乸乛値亖乷乮侾亄値俀乯亊値俀乛俀乸乛値
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖乮侾亄値俀乯亊値乛俀
偲側傝傑偡丅
- 乽嬀偺崙偺傾儕僗崌寁乿傛傝
夞摎丒偦偺侾
乮儁儞僱亅儉丗Satou乯
嵟屻偺栤戣偼婰崋傪悢帤偵抲偒姺偊傟偽傢偐傝傗偡偄丅
偦傟偵忦審偐傜摎偊偼仮偐仜偐仩偩偐傜偁偲偼徚嫀朄丅
摎偊偼仩偱偡丅
夞摎丒偦偺俀
乮儁儞僱亅儉丗Mizutani乯
丠偺偲偙傠偼廲墶傛乕偔峫偊偰弌棃傑偟偨丅偳偆偱偡偐丠
丂丂
丂仢仮仜仩仚
丂仜仩仚仢仮
丂仚仢仮仜仩
丂仮仜仩仚仢
丂仩仚仢仮仜
傛偭偰丄丠偼仩丂偲側傝傑偡丅
夞摎丒偦偺俁
乮儁儞僱亅儉丗akihiro乯
扨搧捈擖偵摎偊傪尵偄傑偡偲丄偢偽傝
巐妏宍乮仩乯偩偲巚偄傑偡丅
夝偒曽偼丒丒丒側傫偐儊乕儖偩偲昞尰偟偵偔偄偺偱偡偑丒丒丒
乽嵍夞傝偵侾僐旘偽偟乿丒丒丒偺傛偆側姶偠偩偲巚偄傑偡丅
姰惉恾偼丄師偺傛偆偵側傞偲巚偄傑偡丅
仢仮仜仩仚
仜仩仚仢仮
仚仢仮仜仩
仮仜仩仚仢
仩仚仢仮仜
弶婜攝抲偼丄
仢仮仜仩仚
仚
偱偟偨丅偙偙偱傢偨偟偼偙偆屽傝傑偟偨丅
仢仮仜仩仚
仚
仚
偱偼側偄偐偲丅偦偟偰仚傪慡晹杽傔偰傒傑偡偲丄
仢仮仜仩仚
仚
仚
丂丂丂仚
丂仚
偙偆傢偨偟偼屽偭偨偺偱偡丅偙傟偑偆傑偄嬶崌偵偼傑偭偰丄
仢仮仜仩仚
仜仩仚仢仮
仚仢仮仜仩
仮仜仩仚仢
仩仚仢仮仜
偲偄偆恾宍偑姰惉偟傑偟偨丅
偳偆偱偟傚偆偐丅偙偠偮偗偲偄偭偰偟傑偊偽偦傟傑偱偱偡偑丄
丒丒丒杮摉偵岥偱尵偆偺偼擄偟偄偺偱偡偑丄
嵍夞傝偵俀僐旘偽偟丒丒丒偙傟偑僉乕儚乕僪偩偲
巚偄傑偡丅
夞摎丒偦偺係
乮儁儞僱亅儉丗Hungry Bear乯
堦斣忋偺楍偺暲傃傪曄偊偢偵嵍偵俀儅僗偢傜偡偲俀抜傔偺暲傃偵側傞
摨偠傛偆偵弴斣偵俀儅僗偢偮嵍偵偢傜偟偰偄偔偲丏丏丏
媡偵丠偐傜俀儅僗塃偺忋丄偦偺傑偨俀儅僗塃偺忋丏丏丏偲弴偵忋偵忋偑偭偰偄偔
偲堦斣忋偺楍偺仩偵偨偳傝拝偒傑偡丅
僐儊儞僩
乮儁儞僱亅儉丗Hungry Bear乯
Microsoft 偺乽僄儞僇儖僞俋俈丂僄儞僒僀僋儘儁僨傿傾乿
乮俠俢亅俼俷俵斉昐壢帠揟乯偺乭杺曽恮乭
偺崁栚偵偁偭偨偺偱敳悎偟傑偡丅
儔僥儞曽恮偼丄杺曽恮偲帡偨偲偙傠傕偁傞偑丄傕偲傕偲偪偑偆傕偺偱偁傞丅
師偺曽恮偼1, 2, 3偱偮偔傜傟丄
偳偪傜傕奺峴丄奺楍偵摨偠悢偑偱偰偙側偄傛偆偵側偭偰偄傞丅
1 2 3 1 2 3
2 3 1 3 1 2
3 1 2 2 3 1
忋偺2偮傪壓偺傛偆偵偐偝偹偰傒傞偲丄偳偙偵傕摨偠儁傾偼偱偰偙側偄丅
1,1 2,2 3,3
2,3 3,1 1,2
3,2 1,3 2,1
偙偺傛偆偵儁傾傪攝楍偟偨丄偳偙偵傕摨偠儁傾偺偁傜傢傟側偄曽恮傪丄
僊儕僔傾丒儔僥儞曽恮偲偄偆丅
嵟弶偵偙傟傪峫偊偨僗僀僗偺悢妛幰僆僀儔乕偺柤傪偲偭偰丄
僆僀儔乕曽恮偲偄偆偙偲傕偁傞丅
儔僥儞曽恮偲僆僀儔乕曽恮偼丄摑寁妛傗捠怣岺妛側偳傊偺墳梡傕偁傝丄
拲栚偝傟偰偄傞丅
Microsoft(R) Encarta(R) 97 Encyclopedia. (俠) 1993-1997 Microsoft
Corporation. All rights reserved.
僐儊儞僩
乽悈偺棳傟乿偝傫偑7/14晅偗偺挬擔怴暦偵偙傫側傕偺偑偁偭偨傛偲嫵偊偰偔偩偝偄傑偟偨丅
儖亅儖
- 嬻偄偰偄傞儅僗偵侾偐傜俋傑偱偺悢帤偺偳傟偐偑擖傝傑偡丅
- 廲偺楍乮俋楍偁傝傑偡乯丄墶偺楍乮偙傟傕俋楍乯丄
懢慄偱埻傑傟偨俁亊俁偺僽儘僢僋乮偦傟偧傟偑俋儅僗偁傞僽儘僢僋偑俋屄乯
偺偄偢傟偵傕丄侾偐傜俋傑偱偺悢帤偑侾偮偢偮擖傝傑偡丅

摎偊
巹偑垽撉偟偰偄傞嶨帍乽僀儔僗僩儘僕僢僋乿乮擔杮暥寍幮姧乯
偵傕枅寧丄弌戣偝傟偰偄傑偡丅僫儞僶亅僾儗僀僗丄棯偟偰乽僫儞僾儗乿
偲屇傫偱偄傑偡丅擄堈搙偺崅偄傕偺偼杮摉偵庤嫮偄偱偡丅
乽偙偆偄偆栤戣傪嶌傞偺偭偰偳偆偡傞偺偐側偁丒丒丒丠乿
側傫偰巚偄側偑傜夝偄偰偄傑偡丅
擄堈搙傪峫偊偰丄柕弬側偔夝偗傞傛偆偵丄
偟偐傕夁晄懌側偔弶婜抣傪梌偊傞偺偭偰寢峔傓偢偐偟偄偺偱偼側偄偐偲巚偆偺偱偡偑丒丒丒丅
偱偒傞偙偲側傜丄弌戣幰偵偦偺偁偨傝傪僀儞僞價儏亅偟偨偄偔傜偄偱偡丅
偙偺乽僫儞僾儗乿傕堦庬偺儔僥儞曽恮偲尵偊傞偱偟傚偆偹丅
儔僥儞曽恮亄僽儘僢僋偛偲偺忦審偲偄偆偙偲偱偡偹丅
偦偟偰丄崱夞庢傝忋偘偨乽嬀偺崙偺傾儕僗乿偺栤戣偼幬傔偺忦審傪壛偊偨
儔僥儞曽恮偲偄偆偙偲偵側傝傑偡偹丅




 栠傞
栠傞