問題189 歪んだコイン
どちらの面も等しい確率で出るコインを投げて、表か裏かを当てるのは、五分五分の公平な賭けになります。 では、歪んだコイン(表と裏の出る確率が等しくない。0でもない。)で、公平な賭けをするには、どうしたらいいでしょうか。
問題の出典
続・とっておきの数学パズル
ピーター・ウィンクラ―著
日本評論社
解答
〜到着順にご紹介します〜
解答・その1
(ペンネ−ム:haya)
表の出る確率を n とする。先ず、n を求めます。
表が出た時に得るポイントを 1-n とし、裏が出た時に得るポイントを n とする。
これで期待値が五分五分になる。
解答・その2
(ペンネ−ム:転位反応)
歪んだコインを投げて、表が出る確率をn、裏が出る確率を1−nとする。
ここで、0<n<1、かつ、n≠1/2。
さて、このコインを2回続けて投げ、1回目、2回目の結果の組み合わせとそれが起こる確率は以下の通りである。
表表 n2
裏裏 (1−n)2
表裏 n(1−n)
裏表 (1−n)n
ここで、n(1−n)=(1−n)nなので、表裏と裏表が起こる確率は等しい。
よって、コインを2回続けて投げ、表裏、裏表の何れの順序となるかで勝負すれば公平な賭けとなる。
但し、表表、または裏裏となった場合にはやり直すものとする。
解答・その3
(ペンネ−ム:まーりんandさとりん)
コインを2回投げ、表→裏と連続で出たらAさんの勝ち、
裏→表と出たらBさんの勝ちとする。
ただし、表→表または裏→裏となった場合は、引き分け
として最初からやり直す。
(理由)
表が出る確率をαとすると、表→裏、裏→表と出る確率
はともにα(1−α)で等しいため公平。また、2回投
げて表→表、裏→裏となった場合は続けずに、一旦終わ
りにしなければ公平にならない。
解答・その4
(ペンネ−ム:迷子の雄猫)
解答1:
コインを2度投げて、「表、裏」の順で出るか「裏、表」の順で出るかを賭ける。
表か裏が連続して出た場合にはやり直す。
表の出る確率をpとすると、どちらも確率が p(1-p) で公平になるから。
解答2:
市松模様の床の上にコインを投げる。
コインがどちらの色の上に落ちるかを賭けるか、
白かつ表、黒かつ裏ならAの勝
黒かつ表、白かつ裏ならBの勝とする。
解答・その5
(ペンネ−ム:ちょろんは太太)
コインのルールを次のように定める。
1回目は、コインの表・裏を決めるために投げる。
2回目は、1回目のコイントスのやり直しを決めるために投げる。
1回目と同じ面が出ると、最初からやり直しとする。
1回目と違う面が出ると、1回目の表・裏で決まりとする。
表の出る確率を q とすると、裏の出る確率は 1-q
表で決まる確率は、1回目が表、2回目が裏なので、q(1-q)
裏で決まる確率は、1回目が裏、2回目が表なので、(1-q)q
それ以外は、やり直しなので、表で決まる確率と裏で決まる確率は相等しい。
解答・その6
(ペンネ−ム:浜田 明巳)
コインにおいて,大きな数が書いてある面が表,年号が書いてある面が裏ということになっている.つまり表,裏の厳密な定義はない.コインごとに慣習的に決まっているだけと考えてよい.
故に歪んだコインの表,裏もそんなにはっきりと定義されている訳ではないと解釈できる.
第三者にそのコインの表,裏を定めてもらう.常識的な呼び名と紛らわしい場合は,「オモテ」、「ウラ」としてもよいし,「H」、「T」と呼んでもよい.勿論かけをする2人にはどちらが「オモテ」、「ウラ」(「H」,「T」)となっているか分からないようにする.
この状態でかけをすれば,公平なものとなる.
このことを証明する.
歪んだコインの表,裏の出る確率をそれぞれp,1−p(0<p<1)とする.
第三者が表をオモテ,裏をウラとする確率と,表をウラ,裏をオモテとする確率は共に1/2とする.
i).第三者が表をオモテ,裏をウラとするとき,A,Bの2人がそれぞれオモテ,ウラを選んで,Aがかけに勝つ確率は,
p/2
A,Bの2人がそれぞれウラ,オモテを選んで,Aがかけに勝つ確率は,
(1−p)/2
ii).第三者が表をウラ,裏をオモテとするとき,A,Bの2人がそれぞれオモテ,ウラを選んで,Aがかけに勝つ確率は,
(1−p)/2
A,Bの2人がそれぞれウラ,オモテを選んで,Aがかけに勝つ確率は,
p/2
まとめると,A,Bがそれぞれオモテ,ウラを選んで,Aがかけに勝つ確率は,
p/2+(1−p)/2=1/2
A,Bがそれぞれウラ,オモテを選んで,Aがかけに勝つ確率は,
(1−p)/2+p/2=1/2
故にこれは公平な賭である.
何回もかけを繰り返す場合は,その都度第三者がオモテ,ウラを決めればよい.
第三者がいまいち信用できない場合は,決めた結果をどこかに書き留めておき,かけをする2人に知られることのないようにすればよい.
解答・その7
(ペンネ−ム:Asterisk*)
コインを二回投げます。
表が出て、裏が出るか、
裏が出て、表が出るか、
のどちらかに賭けます。
表表、裏裏の場合はやり直し。
仮に、表と裏の出る比率がが 2:1 だとして
表 表 裏
表表裏表表裏表表裏
引引甲引引甲乙乙引
フェアな勝負ができます。
解答・その8
(ペンネ−ム:T_Tatekawa)
投げたコインで表が出る確率を A,裏が出る確率を (1-A) とします.
1回投げただけでは確率が等しくならないので,2回投げる事を考えます.
表表の確率:A*A
表裏の確率:A*(1-A)
裏表の確率:(1-A)*A
裏裏の確率:(1-A)*(1-A)
ここで「表裏」と「裏表」の確率が等しい事に注目します.
前者を X, 後者を Y とします.
X になるか Y になるかを当てる賭けをします.
2回コインを投げて,2回とも同じ面が出たらやり直します.
異なる面が出た時に,賭けの当たりを判定します.
賭けに時間がかかってしまいますが,これで公平な賭けが成立します.
やり直しの確率は A2 + (1-A)2 です.
解答・その9
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
歪んでいないコインは裏と表がでる確率は0.5で同じです。
従って、公平な賭けけが出来ます。
歪んでいるコインは表と裏が出る確率は違います。どちらかの出る確率が高くなります。
表と裏の出る確率を合計すると1になります。
従って、公平に賭けをするには2回ずつ振って賭けると同じ確率になります。
そこで、最初に表が出て2回目に裏が出た時に表とし、
最初に裏が出て2回目に表が出た時に裏と決めて掛けをすれば両方とも同じ確率の条件になります。
それ以外はもう一度振り直して賭けをする事になります。
解答・その10
(ペンネ−ム:次郎長)
「表」あるいは「裏」ではなく、
B−1:「表」「裏」が出るか
B−2:「裏」「表」が出るか
2回セットでかける、が正解ではないでしょうか?
つまり、表・表もしくは裏・裏のように、同じ面が2回続けばそれは外す。、
その内に、「表」「裏」もしくは「裏」「表」と必ずなるので、しかもその出る確率は等しい。
仮に「表」「裏」にかけていれば
コインが
表・表・表・裏と出れば最初の2回(表・表)は消えて、3回目/4回目の表・裏が当たったので勝ち
仮にコインが裏・裏・表・表・表・表・裏・裏・裏・表と出れば
最初の8回は消えて、9回目/10回目に裏・表が出たので負けとなる。
整理すると、
表と裏のセットでかける。
表表、裏裏と2回同じ面が連続したトスは無視する。
解答・その11
(ペンネ−ム:夜ふかしのつらいおじさん)
反復試行の確率を考えます。
コインを投げて、表が出る確率をp、裏が出る確率をqとします。(p+q=1)
これをn回くり返すと、表がちょうどr回出る確率は、nCr pr qn-r となります。
また、表の出る回数の期待値は、次の計算より np となります。
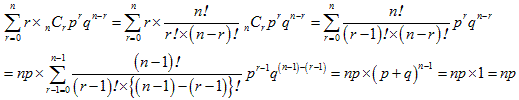
さて、普通のコインを1回投げることを考えます。( p = q = 1/2 )
この試行の事象は、{表,裏}です。
期待値は、np = 1/2 です。
この解釈を次のようにしてみます。
ア)表に賭けるのは、表が1回なので、期待値より大きな回数に賭けること
裏に賭けるのは、表が0回なので、期待値より小さな回数に賭けること
イ)表に賭けるのは、表が1回なので、表の回数が奇数に賭けること
裏に賭けるのは、表が0回なので、表の回数が偶数に賭けること
●ア)について、
普通は、表の確率pも裏の確率qも等しいので、期待値の大小どちらに賭けても公平です。
さて、コインをn回投げるとき、p = q = 1/2 なら、表の出る回数を確率変数Xとした確率密度関数 f(x) の
グラフが期待値に関して左右対称になるので、期待値以下の確率(図の青)と期待値以上の確率(図の黄)が
等しくなります。
一般的に、確率は、離散的な場合は該当する確率の和、連続的な場合はその領域の面積になります。
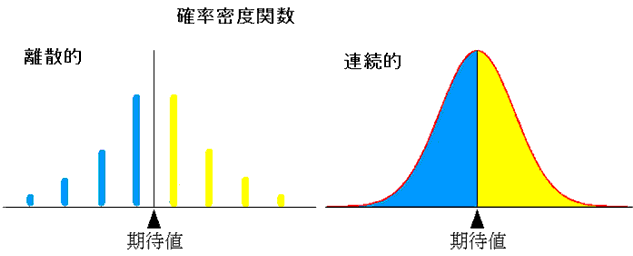
連続的な確率変数の場合は、左右対称でない確率密度関数の場合も、期待値の上下の確率は同じです。
しかし、離散的な確率変数の場合は、注意が必要です。

(2)はコインを投げる回数を増やすとそれぞれの確率は 1/2 に近づきますが現実的ではありません。
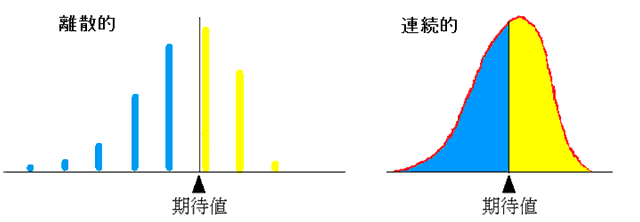
よって、コインをn回投げて表の出る回数が期待値以上か以下での公平な賭けは成立しません。
何より表の出る確率pを知らないことにはどうしようもありません。
●イ)について、
普通のコインは、表も裏も出る確率が 1/2 なので、表の出る回数の偶数、奇数のどちらに賭けても公平です。
何回コインを投げても、表が偶数回出る確率と奇数回出る確率は等しくなります。
これは ( p - q )n = 0 を踏まえて、
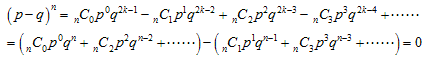
となるからです。
表と裏の出る確率が異なる場合は( p ≠ q )、
表が偶数回出る確率と奇数回出る確率は等しくなりません。(( p - q )n ≠ 0 )
やはり、コインを投げる回数を増やすとそれぞれの確率は 1/2 に近づきますが現実的ではありません。
●次にまったく違うことを考えてみます。
コインの直径の2倍の間隔で十分な本数の平行線を引きます。
コインを適当に投げて平行線にかかるか、かからないかを考えます。
コインの中心の縦方向の位置を考えれば、どちらの確率も 1/2 であることが分かります。
しかし、これはコインの表裏の出方と関係ないので筋違いです。
●そこで、表が出る確率p、裏の出る確率qが分からなくても公平になることを考えます。
積の交換法則 p × q = q × p
を踏まえ、コインを2回続けて投げることを1回の試行とします。
この試行には{表表,表裏,裏表、裏裏}の4つの事象があります。
このうち{表表,裏裏}はそれぞれの確率が分かりません。
しかし、{表裏,裏表}のそれぞれの確率が等しいことは明らかです。
だから、{表表,裏裏}はあいこにして、{表裏,裏表}のどちらかに賭けることにすれば公平になります。
解答・その12
(ペンネ−ム:スモークマン)
同じ確率のコインを使っての勝負に持って行くという方針で...
{(表-裏) or (裏-表) のセットで考えたら等確率}の1枚のコインと見なせるので...
2回投げて1個のコインと考える...
で...
たとえば...(表-裏)の順で出れば「表」("裏"でもいい)
(裏-表)の順で出れば「裏」("表"でもいい)
と取り決めて投げればいいように思えました♪
残りの場合は...(表-表)、(裏-裏) は等確率のコインとは考えられないから...無視ってことで...^^;
解答・その13
(ペンネ−ム:オヤジ)
2回ずつ投げる試行をAとすると
A={(1回目,2回目)|(表,表),(表,裏),(裏,表),(裏,裏)}
ここで、例えば表が出やすいとして一般性を失わないから,
表が出る確率をP,裏が出る確率をQ(=1−P)とすると
1>P>Q>0 ,P+Q=1 さらに Aの各事象は、独立かつ排反だから
P(A)=P2+PQ+QP+Q2=(P+Q)2=1
従って2回ずつ投げる試行においては,確率の期待値が1となり公平な賭けと言える。
解答・その14
(ペンネ−ム:えすわん)
賭けをする2人をAさんとBさんとします。
Aさんはコインのいずれかの面に“1”、反対の面に“2”とでも書きます。
AさんはBさんに、“1”と“2”を書いたことを伝えます。
Bさんは“1”か“2”のいずれかに掛けます。
コインを投げてBさんが掛けた数字が出たらBさんの勝ち、出なかったらAさんの勝ち。
念のため、コインをひっくり返して、反対の面の数字を確認した方がいいですね。
<公平な賭けであることの証明>
コインの表が出る確率をa、裏が出る確率を(1−a)とします。
Bさんは、どっちが“1”か“2”か知らないわけですから、“1”を選ぶとしても一般性は失われない。
Aさんがどちらの面に“1”を書くかは1/2。
そうすると、コインを投げて“1”が出る確率は、
(Aさんが表に“1”を書いて、表が出る)+(Aさんが裏に“1”を書いて、裏が出る)
=1/2×a+1/2×(1−a)
=1/2
2人の役割分担、すなわち、コインに数字を書く役割と、掛ける役割との
どちらを取るかで、2人がもめる可能性がないわけではありませんが、
知恵のある2人の紳士(淑女)なら、確率的に同じだからと、もめることはないでしょう。
コメント
解答の公開が遅れ、ご迷惑をおかけしました。
歪んだコインでも、やり方を工夫することで、公平な賭けができるって、不思議ですね。
 top
top