���186�@�����Z�E�����Z
�W��ނ̋L���@�����������������@�́A���ꂼ��U�������P�`�X�܂ł̂����ꂩ�̐����ł��B ���������͂���܂���B ���}�̂悤�Ȍ��ʂ��킩���Ă���Ƃ��A���̖₢�ɓ����Ă��������B �������A�������́A�S�̈ʂ̐��������A�\�̈ʂ̐��������A��̈ʂ̐��������̂R�����̐�����\���܂��B ���̌��ʂ́i�A�j�́A�R�����̐����ǂ����̘a�ŁA�i�C�j�͂R���̐����ǂ����̍��ł��B
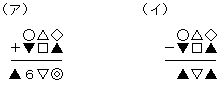
(1)�@���������߂Ă��������B
(2)�@�����������������߂Ă��������B
���̏o�T
��l�̎Z���p�Y��
�͐���
���R������
�������w�@���w�Z(2006�N)
��
�`�������ɂ��Љ�܂��`
�E����1
�i�y���l�|���Fhaya�j
��(1)�F ��=1, ��=2
��(2)�F ��=3, ��=8, ��=7, ��=9, ��=5, ��=4
�y�������z
�̐����̑����Z�ł�10�̈ʂ͂�������1��聣=1�A���Ɉ�����1�������Ȃ����Ƃ�聞=2�B
��𑫂��� ��=3�B
��+�� �� ��-�� ����̈ʂ́��B
��+���� 16 �ł��邱�Ƃ��A��=8, ��=7, ��=9,
��=5, ��=4�B
�E����2
�i�y���l�|���F���q�̗Y�L�j
���`�F�@�������{�����������U����
���a�F�@�������|���������@������
�܂��A����1�͎����B999+999��1998�Ȃ̂ŁA3���̐������m�̘a��2000�����B
��B�̈�̈ʂ��A������1��������1�Ȃ̂Ł���2�B
��A�̈�̈ʂ��A����3�B
�����̏\�̈ʂ��A���Ɂ��𑫂��Ă������灠�������Ă���̈ʂ����ɂȂ�̂�����A����5�B
����ā��Ɓ��͏��s����1��6�A2��7�A3��8�A4��9�̂����ꂩ�ɂȂ邪�A
�L���͂��ꂼ��ʁX�̐�����\���Ă���̂ŁA���Ɓ���4��9(���s��)�łȂ���Ȃ�Ȃ��B
���āAA���̏\�̈ʂŌJ��肪����Ɖ��肷��ƕS�̈ʂ�8��7�A�J��オ�肪�Ȃ��Ɖ��肷���9��7�B
9�͊��ɕʂ̋L���ɓ��Ă͂܂�Ƃ킩���Ă���̂ŁA�S�̈ʂ�8��7
���́����傫���AA���̏\�̈ʂŌJ��肪����̂Ł��́����傫���B
����ā��A���A���A���͏���8�A7�A9�A4�B
�@�W�X�Q
�{�V�T�P
�P�U�S�R
�@�W�X�Q
�|�V�T�P
�@�P�S�P
�E����3
�i�y���l�|���F�X���[�N�}���j
�܂Ƃ߂Ėʓ|�ł܂��� ^^
���オ��́�=1...��-��=�� ����...��=2
��+��=16 �� ��-��=1...��=8,��=7
��+��=1��, ��-��=��...��=9,��=5,��=4
�ƁA�������莎�s���낷��Γ��Ă͂܂���̂����܂�...^^;
���ۂ�...
892 + 751 1643 892 -751 141
�ŁA�������Ă��邵...�c��́���3�Ƃ킩���
�����...
(1)�@���������߂Ă��������B
�@�@����=12
(2)�@�����������������߂Ă��������B
�@�@������������=387954
�ł��� ^^
�E����4
�i�y���l�|���F���Y���j
�i�A�j�̎���聣���P��������B
���Ɂi�C�j�̂P�̈ʂ́��[�P���P�ƂȂ�̂ŁA�����Q�ƂȂ�A
����Ɓi�A�j�̎����灝�����i�Q�j�{���i�P�j���R�ƕ�����
���Ɂi�A�j�́��{�����P�U�Ȃ�A�i�A�j�̂P�O�̈ʂ́��{�������ƁA�i�C�j�̂P�O�̈ʂ́��[����������������̂ŁA
�i�A�j�̂P�O�O�̈ʂ́��{�����͂P�T�łP�O�̈ʂ���P�i�P�O�O�j�J��オ�������Ƃ�������B
�܂�@�i�A�j�̂P�O�̈ʂ́��{�������{�P�O
�@�@�@�@�i�C�j�̂P�O�̈ʂ́��[�������@�@�@�@�@�ƂȂ�̂ŁA�������{�T
���łɁA�P�C�Q�C�R�͎g���Ă��܂��Ă���̂ŁA��L��������̂́��i�X�j�����i�S�j�{�T�����Ȃ��B
�����Łi�A�j�̎��������
�@ ���X�Q
�{ �����P
�[�[�[�[�[�[
�@�P�U�S�R�@�@
�@
�ƂȂ�B�@�܂�@�����T�A�@�J��オ��O�́@���{�����P�T�����Łi�C�j�̎��������
�@�@���X�Q �[�@���T�P �[�[�[�[�[ �@�@�P�S�P
���{�����P�T �� ���[�����P�@�@�@����@�@�����W�A�����V
�ȏ���A
�i�P�j�������P�Q
�i�Q�j���������������R�W�V�X�T�S
�E����5
�i�y���l�|���F�Y���j
�E����6
�i�y���l�|���F�}�V���j
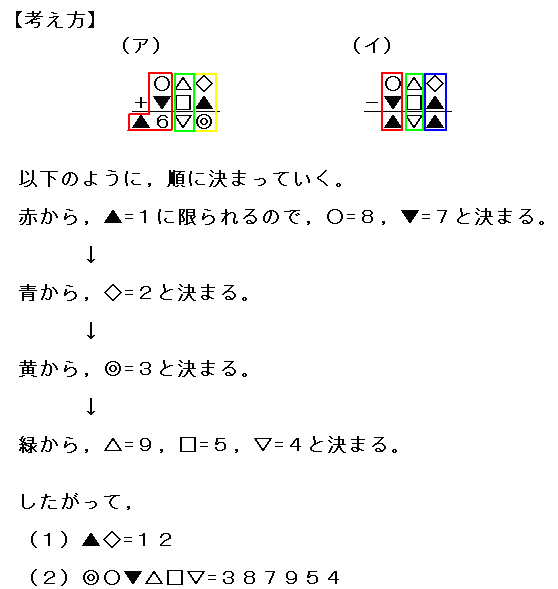
�y�z
�P
�܂��A�����Z�̐�̈ʂɒ��ڂ���
�J��オ�肪����̂͂P����
������@�����P
�Q
�����Z�̈�̈ʂɒ��ڂ���
���[�������Ȃ̂Ł����Q
�R
�����̕S�̈ʂɒ��ڂ���
���Ɓ��𑫂���16 or 15, ������1 or 2�Ȃ̂ʼn\��������̂�
(��,��)=(9,7),(8,7)
�ǂ���̏ꍇ�������V
���͕ۗ�
�S
�����̏\�̈ʂő����Ă������Ă��������Ȃ̂ŁA�����͑����ČJ��オ��
���̑g�ݍ��킹�́����X�A�����T�A�����S�̂�
�T
�c��́����W�A�����R
�ȏ���A
(1)�����P�A�����Q
(2)�����R�A�����W�A�����V�A�����X�A�����T�A�����S
�E����7
�i�y���l�|���F�]�ʔ����j
(1)���������߂�
�E�v�Z�i�A�j�ɂ����Đ�ʂւ̌J��肪���邱�Ƃ��灣���P
�E�v�Z�i�C�j�ɂ����ā��|�������A�܂聞�|�P���P�Ȃ̂Ł����Q
���̌��ʂ���Ɍv�Z�����������ƈȉ��̒ʂ�B
�i�A�j �@�i�C�j
�@�@�@�@���� 2 �@ ���� 2
�@�@�@�{���� 1 �@ �|���� 1
�@�@�@1 6 �� 3 �@ 1�� 1
�i2�j�����������������߂�
�E��L�̌��������v�Z���i�`�j���A�����R
�E�v�Z���i�A�j�ɂ����āA���{�����P�U�A�v�Z���i�C�j���A�������ł��邱�Ƃ���A
�����X�C�����V�@�܂��́A�J�����l������Ɓ����W�C�����V�̉��ꂩ
�����ŁA�����X�C�����V�̏ꍇ�F�c��̐����͂S�C�T�C�W�ł��邪�A���{�����������g�ݍ��킹���Ȃ�
����A�����W�C�����V�̏ꍇ�F�c��̐����S�C�T�C�X���g���āA�X�{�T���P�S�A�X�|�T���S�̑g�ݍ��킹���ł���
�ȏ�̌��ʂɂ��A�����W�C�����V�C�����X�C�����T�C�����S
�i�A�j �@�@�@�@�@�i�C�j
�@�@�@�@892 892
�@�@�@�{751 �|751
�@�@�@ 1643 141
�E����8
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
����
�����W�@�����X�@���@�Q�@�����V�@�����T�@�����P�@�����S�@�����R
�i�A�j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�C�j
�@�@�@�@�������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@������
�@�@�@�{�������@�@�@�@�@�@�@�@�@�@�@�@�@�@�|������
�@�@�@���U�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@������
�i�A�j�̎��̍��v��ʂ́��͏\�ʂ́��{���̉��Z�ɂ��J��グ�Ȃ̂�1�ł��B
�]���ā����P�ł�
������i�A�j�Ɓi�C�j�ɑ�����܂��B
�Ɓi�C�j�����灞���Q���m�肵�i�A�j���ɑ������Ɓ����R�ƂȂ�܂��B
�i�A�j���̍��v�S�ʂ��U�ɂȂ�̂�
[1]�E�E�E�X�{�V���P�U����[2]�E�E�E�W�{�V�{�i�A�j���̏\�ʂ���̌J��グ�j���P�U�ɂȂ�܂��B
���߂�\�ʂ̐����������͂X�ƂT�ƂS�ɂȂ�܂��̂Ō����܂��B
���Z���Ă������Z���Ă����������ɂȂ遤�͂S�ƂȂ�܂��B
�]���ā@�����X�@�����T�@�����S�@�Ɗm�肵�܂��B
�E����9
�i�y���l�|���F�q����1128�j
�i1�j
����2�ɂȂ�̂́��Ɓ���9�ňꌅ������Q���J��オ���Ă���ꍇ�����Ȃ̂�1�Ɖ�
��܂��B
���́i�C�j����2�ł��B
�i2�j
���́i1�j����3�ł�
�����܂łŎc���Ă��鐔����4,5,7,8,9�ł��B�܂��P���ڂ͂Q���ڂɉe�����܂���B
�i�����j�̑g�ݍ��킹�́A�i�A�j����i8,7�j�E�E�Q���ڂ���1�J��オ���Ă���ꍇ
�Ɓi9,7�j�E�E�J��オ���Ă��Ȃ��ꍇ������܂����i9,7�j�Ɖ��肷��Ɓ�������
�i4,5,8�j�ƂȂ萬�����܂���B
�]���āi�����j�́i8,7�j�E�E�Q���ڂ���1�J��オ���Ă���ꍇ�ƂȂ�܂��B
�i�������j�͏�L����P�J��オ��Ȃ���Ȃ�Ȃ��̂Łi�A�j����i5,9,4�j��
�i9,5,4�j�ƂȂ�܂����A�i�C�j�̏������i9,5,4�j�ł��邱�Ƃ�����܂��B
�ȏ�������(�P)(�Q)�̓������܂Ƃ�
�i�����������������j���i1,2,3,8,7,9,5,4�j
���Z���Ă݂��
892+751��1643
892-751��141
�܂��A�i1�j�Ł���������Ɓi�A�j�i�C�j��ό`���ā�6����+���������������~2�Ōv
�Z�����ق����ȒP��������܂���B
�E����10
�i�y���l�|���F�l�c�@�����j
���ʎZ�̓v���O�����̓��ӂȕ���ł��D
�@�����`�C�����a�C�����b�C�����c�C�����d�C�����e�C�����f�C�����g�Ƃ��āC�V���~�Ԃ��ɂP�`�X�i�U�ȊO�j�̐��Ă͂߂āC���藧���̂������D
�@�������v�Z���́C�W�X�Q�{�V�T�P���P�U�S�R�C�W�X�Q�|�V�T�P���P�S�P
�i�P�j�����́C�P�Q
�i�Q�j�������������́C�R�W�V�X�T�S
Option Explicit
'ABC+DEF=F6GH, ABC-DEF=FGF
Sub Macro1()
Cells(1, 1).Value = 0
Dim kuriagari(2) As Integer, gyou As Integer
Dim A As Integer, B As Integer, C As Integer
Dim D As Integer, E As Integer, F As Integer
Dim G As Integer, H As Integer
For C = 1 To 9
If C <> 6 Then
For F = 1 To 9
If F <> 6 And C <> F Then
H = (C + F) Mod 10
If 0 < H And H <> 6 And C <> H And F <> H Then
kuriagari(1) = (C + F) \ 10
For B = 1 To 9
If B <> 6 And B <> C And B <> F And B <> H Then
For E = 1 To 9
If E <> 6 And B <> E And C <> E And E <> F And E <> H Then
G = (B + E + kuriagari(1)) Mod 10
If 0 < G And G <> 6 And B <> G And C <> G And E <> G And F <> G And G <> H Then
kuriagari(2) = (B + E + kuriagari(1)) \ 10
For A = 1 To 9
If A <> 6 And A <> B And A <> C And A <> E And A <> F And A <> G And A <> H Then
D = 10 * F + 6 - A - kuriagari(2)
If A + B + C + D + E + F + G + H = 1 + 2 + 3 + 4 + 5 + 7 + 8 + 9 Then
If (100 * A + 10 * B + C) - (100 * D + 10 * E + F) = 100 * F + 10 * G + F Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = Cells(1, 1).Value * 4 - 3
Cells(gyou, 3).Value = 100 * A + 10 * B + C
Cells(gyou + 1, 2).Value = "+": Cells(gyou + 1, 3).Value = 100 * D + 10 * E + F
Cells(gyou + 2, 3).Value = 1000 * F + 600 + 10 * G + H
Cells(gyou, 6).Value = 100 * A + 10 * B + C
Cells(gyou + 1, 5).Value = "-": Cells(gyou + 1, 6).Value = 100 * D + 10 * E + F
Cells(gyou + 2, 6).Value = 100 * F + 10 * G + F
End If
End If
End If
Next A
End If
End If
Next E
End If
Next B
End If
End If
Next F
End If
Next C
End Sub
�E����11
�i�y���l�|���F�܁[��������Ƃ��j
(1)�@���������߂Ă��������B
�i�A�j�̉��̐�̈ʂ͂P������肦�Ȃ��̂Ł����P
�i�C�j�̉���̈ʂ���������ɂ́����Q
(2)�@�����������������߂Ă��������B
(1)��������i�A�j�i�C�j�͂��ꂼ��A�W�X�Q�ƂV�T�P�̘a�ƍ��Ő��藧�B
����āA
�@�����R
�@�����W
�@�����V
�@�����X
�@�����T
�@�����S
�E����12
�i�y���l�|���F������͑����j
�i�P�j
�i�A�j���A�R�����ǂ����̑����Z������A�J��グ��ꂽ�S���ځ@��= 1
�i�C�j��1���ڂɒ��ڂ���ƁA����P=�P�@������@��=�Q
�i�Q�j
�i�A�j��1���ڂɒ��ڂ���ƁA��=�Q�{�P���R
�i�A�j���Ɓi�C�j����������ƁA�Q���i�����Q�j���P�V�O�O�{�Q���i���O�j�{�S
�P�O�Ŋ����Đ�������ƁA�@�Q���i�����j���P�V�O�{�Q����
�E�ӂ́A�P�V�O�ȏ�A�P�X�O����������A���́A�W�܂��́A�X�B
���Ɓ��́A2�{�ǂ�����1���ڂ������Ȃ̂ŁA�P�ƂU�A�Q�ƂV�A�R�ƂW�A�S�ƂX�̑g�ݍ��킹�B
�P�A�Q�A�R�͂��łɁA�g���Ă���̂ŁA�S�ƂX�B
����āA���͂W�B���Ɓ��́A�����X�A�Ł����S�B
�W�X�Q�{�����P���P�U�S�R�@�@����āA�����P���V�T�P
����āA�����V�A�����T�B
��������ƁA�����R�A�����W�A�����V�A�����X�A�����T�A�����S
�E����13
�i�y���l�|���F�̂�����j
�i�A�j�̐�̈ʂ͖��炩�ɂP�����灣���P
�i�C�j���P�{�P���������灞���Q
�i�A�j���Q�{�P���������灝���R
�i�C�j���P���P�{�����P�������Q
�i�A�j�ɑ�����ĂP���P�{�����P�{�����P���P�U���R
���{�����P�O���K�v�����灠���T
�P�{�P�{���{�����P�U�ƂȂ邩�灥���V
�i�A�j�́����Q�{�V�T�P���P�U���R
�i�C�j�́����Q�|�V�T�P���P���P�@�ƂȂ�c��̐����͂S�A�W�A�X�ł���
�i���A���j���i�S�A�X�j�͂W�{�V���P�U�@�ƂȂ�s�K
�i���A���j���i�X�A�S�j�̎������W�@�@����͑�ӂ���
�E����14
�i�y���l�|���Fyou�j
�i�P�j
���E���́A�i�A�j�̎��̘a�̂S���ڂɁ������Ă��邽��
�������U�������P����X�܂ł̂����ꂩ�̐����ł��邽��
�J��グ�ł��P�����l�����Ȃ��B����āA
�@�@�����P�i���j
�i�C�j�̎��������Z�̂P���ڂ̌v�Z�ɒ��ڂ����
���[�������Ɓi���j���
�@�@�����Q�i���j
���������āA
�����P�A�����Q�ƂȂ�B
�i�Q�j
�i�A�j�̂P���ڂ̎��Ɓi���j�A�i���j���
�@�@���{���������R�i���j
�����Z�ƈ����Z�̂Q���ڂ̎��́A�ȉ��̂悤�ȏꍇ�������ł���B
�i��j�����Z�̂Q���ڂ̎��̘a���\���̏ꍇ
�@�@���{�����P�����P�O�{��(a)
�@�@���[������(b)
(a)��(b)�̘A�����������
�@�@�������{�T
�i��j�����Z�̂Q���ڂ̎����J�艺���������ꍇ
�@�@���{������(a)
�@�@�P�O�{���[������(b)
(a)��(b)�̘A�����������
�@�@�T�{������
�i�O�j�ǂ�����Ȃ��ꍇ
�@�@���{������(a)
�@�@���[������(b)
(a)��(b)�̘A�����������
�@�@������
�������i�O�j�́A�Ȃ�
�i��j�Ɓi��j�̏ꍇ���l������B
�c��̐����͂S�A�T�A�V�A�W�A�X�ł���
�i��j�Ɓi��j�̘A���������̉��̎��ɓ��Ă͂߂��
�i��j�����X�A�����S�A�����T
�i��j�����S�A�����X�A�����T
�����Z�ƈ����Z�̂R���ڂ̎����
���Ɓ��́A�V�ƂW�̐����ƂȂ�
���������
�@�@�����W�A�����V�ƂȂ�
�����Z�̂R���ڂ̎����
�����Z�̂Q���ڂ̎����J�艺���ɂȂ�Ζ������邽��
����āA���������T���
�i��j�̏�������������B
����āA�����R�A�����W�A�����V�A�����X�A�����T�A�����S�ƂȂ�B
�E����15
�i�y���l�|���FT_Tatekawa�j
(1)
�܂��i�A�j��3���̎��R�����m�𑫂��Z���Ă���̂ŁC�a��2000�����ł���D
����� ��=1�D
���Ɂi�C�j�Ł�����1��������1�Ȃ̂ŁC��=2�D
(2)
�i�A�j���灝=2+1=3
�i�C�j�Ł�-��=���Ȃ̂ŁC�i�A�j�̏\�̈ʂ͌J��オ�肪�������Ă���D
�@�@�@��+��=10+��
���ӂ𑫂���2�Ŋ���ƁC
�@�@�@��=5+��
����1, 2, 3�ɑΉ�����L�������܂��Ă���̂ŁC
�@�@�@��=9, ��=4
�c�鐔����7, 8�ł���D
�i�C�j�ň����Z�����Ă��鎖���灛�́����傫���D
����ā�=8�C��=7�D
�E����16
�i�y���l�|���FAsterisk*�j
--------------------���1--------------------
�L���̓��͂��ʓ|�Ȃ̂ŁAABCDEFGH�ɂ��܂����B
�i�A�j
�@�@�@ ABC
�@�@�@ +DEF
�@ �@--------
�@�@�@ F6GH
�i�C�j
ABC
--DEF
--------
FGF
�܂�C-F=F�ƂȂ�C��F�̑g�ݍ��킹�Ƃ��Ắi�J�艺������l����Ɓj
�@�@2,1�@4,2�@6,3�@8,4
�@�@2,6�@4,7�@6,8�@8,9
��8�ʂ肪�l�����܂��B
������6�͂��łɎg���Ă���̂ŁA
�@�@2,1�@4,2�@8,4�@4,7�@8,9
������F��6�̍��ɂ����ČJ��オ��ł��B
�J��オ���1�ȏ�ɂ͂Ȃ�܂���B
�����C��F�i���Ɓ��j�́@2��1
--------------------���2--------------------
C��F���������
�i�A�j
�@�@�@ AB2
�@�@�@ +DE1
�@ �@--------
�@�@�@ 16G3
�i�C�j
AB2
--DE1
--------
1G1
�@�@AB2+DE1=16G3�@�@AB2-DE1=1G1
�����
�@�@ABC=x
�@�@DEF=y
�@�@16G3=1000+600+10g+3
�@�@1G1=100+10g+1
�Ƃ���ƁA�A�������������܂��B
�@�@x+y=1603+10g
�@�@x-y=101+10g
�����������
�@�@x+y-1603=x-y-101
�@�@x-x+y+y=1603-101
�@�@2y=1502
�@�@y=751
���ɑ�������
�i�A�j
�@�@�@ AB2
�@�@�@ +751
�@ �@--------
�@�@�@ 16G3
�i�C�j
AB2
--751
--------
1G1
����A-7=1�ɒ��ڂ��܂��B�c���Ă��鐔��4,8,9�ł��BA�̌��Ƃ��ẮA8��9������܂��B
�iB-5�̌v�Z�̍ۂɌJ�艺���肪�s��ꂽ�Ƃ��ɂ�9���K�v�Ȃ̂ŁB�j
����A��8�Ƃ��āA8-7=1�Ƃ���ƁA
�����ZB+5=G�ɂ����āA8+7��15�ŁA
16�ɂ���ɂ́A�J��オ�肪�K�v�Ȃ��߁A
�@�@B+5��10
�@�@B��5
B�̌��Ƃ��Ďc���Ă����̂�4��9�Ȃ̂ŁA
B��9�A�Ȃ�AG��4
�i�A�j
�@�@�@ 892
�@�@�@ +751
�@ �@--------
�@�@�@ 1643
�i�C�j
892
--751
--------
141
�v�Z�@�Ŋm�F������@�@892+751=1643 �@�@892-751=141
�E����17
�i�y���l�|���F�m�Ɓ`�j
�P�@�a�̐�̈ʂ���@�@�����P
�Q�@�����P�ƍ��̈�̈ʂ���@�@�@�����Q
�R�@�������{�����R
�S�@�a���A���{�����P�U or �P�T�A����聛�����Ȃ̂ŁA�i��,���j���i�X,�V�j���i�W,�V�j
������ɂ��Ă��A�����V
���@���i�K�ŁA�c�����g���鐔���́A�S�C�T�C�W�C�X
�T�@�\�̈ʂɒ��ځB��̈ʂ���̌J��オ��A��̈ʂւ̌J�艺����͂Ȃ��A�a�������������A�����T
�U�@���Ɏg���Ă��鐔���Ƃ̏d����J��オ�蓙���l�����A
�@�����W�A�����X�A�����S
�����P�@�����Q�@�����R�@�����S
�����T�@�����V�@�����W�@�����X
�i�P�j�̓��@
�@�@�P�Q
�i�Q�j�̓���
�@�@�R�W�V�X�T�S
�E����18
�i�y���l�|���F�I���W�j
�i�@�j����@�����P�@��@���̌J��オ�肾����
�i�C�j ����@�������{�����P�{�P���Q
�i�@�j����@�������{�����Q�{�P���R
�i�@�j����@���{�������@�E�E�E�i�P�j�@�@�܂��́@���{�������{�P�O�@�E�E�E�i�Q�j
�@�@�@�@�@�@���{�����P�U�@�E�E�E�i�R�j�@�܂��́@���{�����P�T�@�E�E�E�i�S�j
�i�C�j����@���|�������@�E�E�E�i�T�j�@�@�܂��́@���|���{�P�O�����@�E�E�E�i�U�j
�@�@�@�@�@�@���|�����P�@�E�E�E�i�V�j�@�@�܂��́@���|�����Q�@�E�E�E�i�W�j
�i�R�j�{�i�W�j�C�܂��́i�S�j�{�i�V�j����@�Q�����P�W�C�P�U
�����Ł@�����X�@�Ƃ���Ɓ@�����V�@��i�R�j�C�i�W�j
�@�@�@�@�����W�@�Ƃ���Ɓ@�����V�@��i�S�j�C�i�V�j
�]���ā@���@�����V�@�@�@�܂��@�i�P�j�Ɓi�T�j�C�i�Q�j�Ɓi�U�j�͖���
�]���ā@�i�P�j�{�i�U�j����@�Q���{�P�O���Q���@�E�E�i�P�O�j�i�������j�@�܂���
�@�@�@�@�i�Q�j�{�i�T�j����@�Q�����Q���{�P�O�@�E�E�i�P�P�j�i�������j
�]���ā@�i�P�O�j�C�i�P�P�j����@�����T�@���̂��Ƃ��@�����W�C�X
�����Ł@�i�P�O�j�́A���蓾�Ȃ��B�@�i�P�P�j�ɂ����ā@�����W�@�Ƃ����
�� ���R�ƂȂ�@�����R�Ɩ����A�@���@�����X�C�����S�C�����W
�]���ā@(1)�@ �����P�C�����Q
�@ �@�@�@(2) �����R�C�����W�C�����V�C�����X�C�����T�C�����S�@
�E����19
�i�y���l�|���FPart Marty�j
�P�j�ꌅ�̐����̑����Z�͂P�W�ȉ��Ȃ̂Ł� = 1�������肦�Ȃ��B
�� - �� = ���܂聞 - 1 = 1�]���ā� = 2�� + �� = ���܂�2 + 1 = ���]���ā� = 3
�Q�j�W��ނ̋L��������������������a,b,c,d,e,f,g,h�Ƃ��܂��B
������ = a * 100 + b * 10 + c
������ = d * 100 + e * 10 + f
������ + ������
s1 : f + 10 * e + 100 * d + c + 10 * b + 100 * a = h + 10 * g + 1000 * f + 600
������ - ������
s2 : - f - 10 * e - 100 * d + c + 10 * b + 100 * a = 10 * g + 101 * f
s1,s2���
s3 : f = - (h - 20 * e - 200 * d + 600) / 897
s4 : c = - (34 * h - 2990 * g - 3670 * e - 36700 * d + 2990 * b + 29900 * a + 20400) / 299
s3���A20 * e - h��200 * d - 600 - 897 �ƂȂ�@d = 7
s3 : f = - (h - 20 * e - 800) / 897�ƂȂ�@e = 5
s3 : f = - (h - 900) / 897�ƂȂ� h = 3
f = 1
s4 : c = 10 * g - 10 * b - 100 * a + 852�ƂȂ� a = 8
s4 : c = 10 * g - 10 * b + 52�ƂȂ�
�c��̐����́A2,4,9�Ȃ̂�
b = 9,g = 4,c = 2�ƂȂ�B
�]����a = 8,b = 9,c = 2,d = 7,e = 5,f = 1,g = 4,h = 3
892 892 +751 -751 1643 141
�E����20
�i�y���l�|���F�O�p��K�j
(1)
�@�@ (�A)��100�̈ʂ̘a ���{����19 ������ �����P�B
�@�A (�C)�̂P�̈ʂ̍� ���|�P���P ���C�����Q�B
(2)
�@�B (�A)�̂P�̈ʂ̘a �Q�{�P�������R
�@�C 100�̈ʂ̘a��� ���{����16�C���|�����P ���C�����W or �X�C�����V
�@�D �����W �̂Ƃ��C�����X�C�����T�C�����S �ƂȂ�K�B
�@�E �����X �̂Ƃ��C�����S�C�����T�C�����X �ƂȂ邪�C���������X �ƂȂ��Ă��܂��s�K�B
�ȏ���C���̕��ʎZ�̉��́C
�@�@�@�W�X�Q�@�@�W�X�Q
�@�@�{�V�T�P�@�|�V�T�P
�@�@�|�|�|�|�@�@�|�|�|
�@�@�P�U�S�R�@�@�P�S�P
�E����21
�i�y���l�|���F��ӂ����̂炢��������j
�R�����g
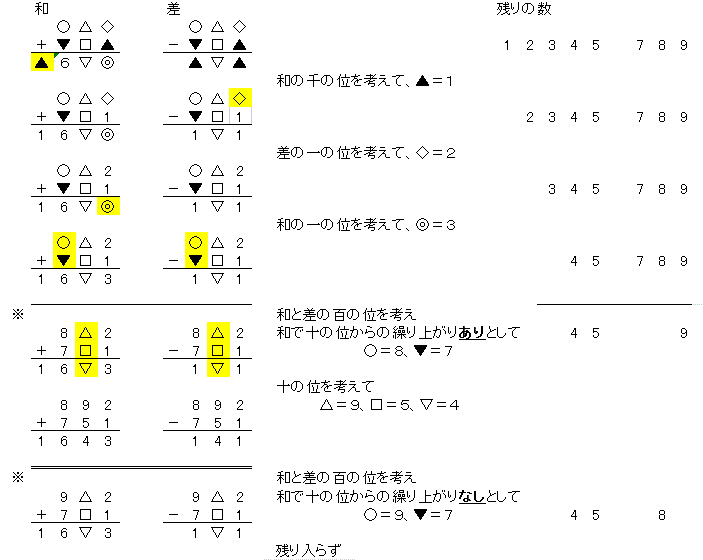
���̂悤�Ȗ��ʎZ�Ƃ����܂��ˁB �\���͗L���ł����A�����Ɍ����I�ɁA ��������Ӑ��i���ɉ��͂Ȃ����Ɓj���m�ۂ��Ȃ���������߂�K�v������܂��B ����̖��͂Q���̘a�ƍ��ł���Ƃ����̂��������낢�ł��ˁB
 top
top